2-2cdot 2cdot 4cdot frac12= 12.
4. По теореме Пифагора LH= sqrt = sqrt <12-1>= sqrt <11>.
5. S_= frac12(KM+LN)cdot LH= frac12(3+1)cdot sqrt <11>= 2sqrt <11>.
Ответ
Задание №1185
Условие
В правильной четырёхугольной призме ABCDA_1B_1C_1D_1 сторона основания равна 9 , боковое ребро равно 14 . Точка K принадлежит ребру A_1B_1 и делит его в отношении 2:7, считая от вершины A_1.
а) Докажите, что сечение призмы плоскостью, проходящей через точки A , C и K , является равнобедренной трапецией.
б) Найдите площадь этого сечения.
Решение
а) Плоскость сечения пересекает плоскость верхнего основания по прямой, проходя-щей через точку K и параллельной AC (по свойству параллельности плоскостей). Тогда плоскость AKC пересекает ребро B_1C_1 в точке L так, что KL parallel AC. Следовательно, искомым сечением будет трапеция AKLC .
KB_1parallel AB, B_1Lparallel BC, KLparallel AC. 2>= 10sqrt 2.
2>= 10sqrt 2.
AC=ABsqrt 2=9sqrt 2; KL =frac79AC=frac79cdot 9sqrt 2=7sqrt 2.
Так как трапеция AKLC — равнобедренная, имеем
Из riangle AKH,, KH= sqrt = sqrt <200-2>= sqrt <198>.
S_=frac2cdot KH,= 8sqrt 2cdot sqrt <198>=48sqrt <11>.
Ответ
Задание №1180
Условие
В правильной четырёхугольной призме ABCDA_1 B_1C_1 D_1 сторона основания равна 7 , а боковое ребро — 12 . На рёбрах A_1D_1, C_1D_1 и CB взяты точки F, К, L соответственно так, что A_1F=C_1K=CL=3.
а) Пусть P — точка пересечения плоскости FKL с ребром AB . Докажите, что FKLP — прямоугольник.
б) Найдите площадь сечения призмы плоскостью FKL.
Решение
а) Найдём положение точки P . Эта точка пересечения плоскости FKL и ребра AB, лежащего в плоскости ABCD.
Плоскость ABCD параллельна плоскости A_1B_1C_1D_1, в которой лежит отрезок KF. Плоскость FKL пересекает параллельные плоскости ABCD и A_1B_1C_1D_1 по параллельным прямым, отсюда KF parallel LP. 2>= PK. Диагонали параллелограмма равны, следовательно, FKLP — прямоугольник.
2>= PK. Диагонали параллелограмма равны, следовательно, FKLP — прямоугольник.
б) Пусть Q и R — точки пересечения прямой KF и прямых B_1C_1 и A_1B_1. Проведём прямые RL и QP , они пересекут рёбра CC_1 и AA_1 в точках M и N соответственно. Тогда RC_1=KC_1=CL, поэтому можно доказать, что равны треугольники RC_1M и MCL. Прямая RL , а значит, и плоскость FKL пересекают ребро CC_1 в его середине — точке M . Аналогично плоскость FKL пересекает ребро AA_1 в его середине —точке N .
В диагональном сечении CC_1A_1A, которое является прямоугольником, отрезок MN — средняя линия. В прямоугольнике MCAN противоположные стороны равны: MN=CA=7sqrt 2.
Сечение FKMLPN состоит из двух равных трапеций MKFN и MLPN , причём
мы доказали, что LK perp KF и LK perp LP. Высота каждой из этих трапеций равна frac2=frac<9sqrt 2>2.
S_< ext<сечения>>= 2S_= 2cdot frac2cdot frac2= (4sqrt 2+7sqrt 2)cdot frac<9sqrt 2>2= 99.
При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений.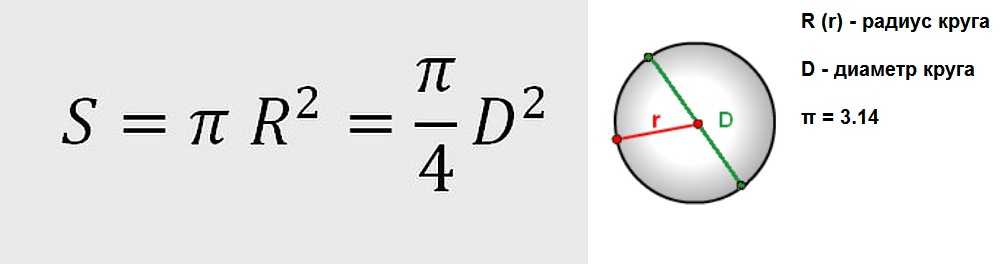 Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
S = πR 2
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
a 2 + b 2 = c 2
Из нее можно вывести такую формулу:
c = S*q*r*t*(a 2 + b 2 )
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
используется в тех случаях, когда сечение идет параллельно двум основаниям.
При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:
где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.
Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:
где 2а – значение хорды, расчета площади поперечного сечения.
В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения.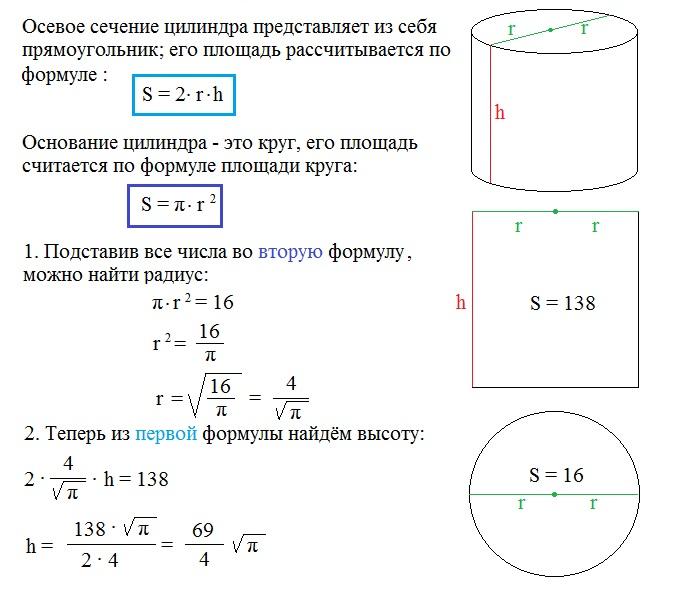 Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека.
Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.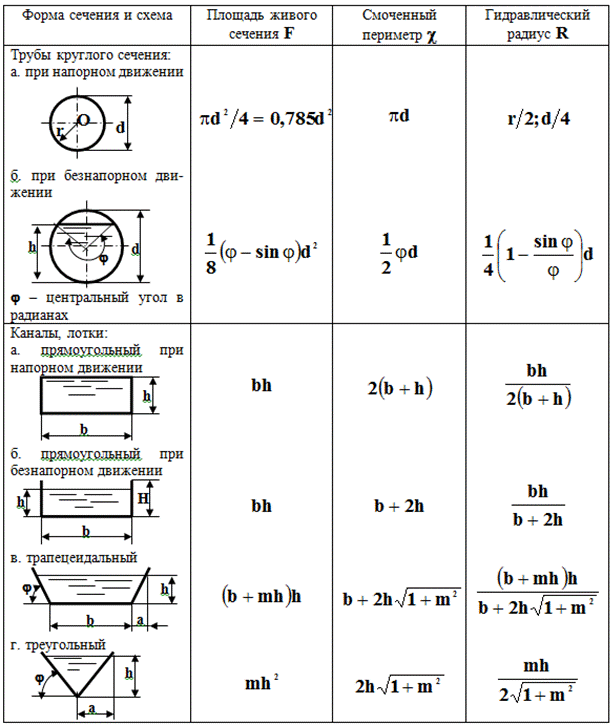
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.

- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Как найти площадь сечения шара площадь сечения шара формула математика
Вопрос № 1: Как правильно задаются закрепления (связи) в системе SCAD Office?
Ответ: Связевые закрепления присваиваются узлам, перемещение или поворот, которых необходимо закрепить, опираясь исключительно на конструктивное решение рассматриваемого строения. При работе SCAD Office различают 6 видов связей: 3 перемещения и 3 поворота относительно 3-х глобальных осей. Закрепления X,Y,Z накалывают запрещение перемещений по соответствующим направлениям осей, а закрепления Ux, Uy, Uz – поворот вокруг глобальных осей.
При работе SCAD Office различают 6 видов связей: 3 перемещения и 3 поворота относительно 3-х глобальных осей. Закрепления X,Y,Z накалывают запрещение перемещений по соответствующим направлениям осей, а закрепления Ux, Uy, Uz – поворот вокруг глобальных осей.
Пример: Закрепление фермы при решении плоской задачи может выглядеть так: левый узел опирания закрепляется по направлению X и Z, правый край по направлению Z
Формула поперечного сечения проводника
Как правило, провода обладают круглым сечением, но допустимые токовые показатели должны рассчитываться согласно площади поперечного сечения
С целью самостоятельного определения площади сечения в одножильном или многожильном проводе осторожно вскрывается оболочка, представляющая собой изоляцию, после чего в одножильном проводнике замеряется диаметр
Площадь определяется в соответствии с хорошо известной даже школьникам физической формулой:
S = π х D²/4 или S = 0,8 х D², где:
- S является площадью сечения в мм2;
- π — число π, стандартная величина, равная 3,14;
- D является диаметром в мм.

Проводник
Замеры многожильного провода потребуют его предварительного распушения, а также последующего подсчета количества всех жилок внутри пучка. Затем измеряется диаметр одного составляющего элемента и вычисляется площадь сечения в соответствии со стандартной формулой, указанной выше. На заключительном этапе замеров суммируются площади жилок с целью определения показателей их общего сечения.
С целью определения диаметра проводной жилы используется микрометр или штангенциркуль, но при необходимости можно воспользоваться стандартной ученической линейкой или сантиметром. Замеряемую жилку провода нужно максимально плотно намотать на палочку двумя десятками витков. При помощи линейки или сантиметра требуется замерить расстояние намотки в мм, после чего показатели используются в формуле:
D = l/n,
Где:
- l представлено расстоянием намотки жилки в мм;
- n является числом витков.
Следует отметить, что большее сечение провода позволяет обеспечивать запас по показателям тока, в результате чего уровень нагрузки на электропроводку можно незначительно превышать.
Чтобы самостоятельно определить проводное сечение монолитной жилы, требуется посредством обычного штангенциркуля или микрометра выполнить замеры диаметра внутренней части кабеля без защитной изоляции.
Основные положения теории оболочек
Большинство
элементов инженерных конструкций в расчетной схеме, подлежащих расчету на
прочность, как это уже было отмечено, связаны с
расчетом бруса, пластинокили оболочек.
Предыдущие
разделы были достаточно подробно посвящены вопросам расчета стержней и
стержневых систем. Настоящий раздел книги посвящен различным вопросам расчета
пластинок и оболочек.
Под оболочкой
понимается тело, одно из измерений которого (толщина) значительно меньше двух
других. Геометрическое место точек, равноотстоящих от обеих поверхностей
оболочки, носит название срединной поверхности.
Если срединная
поверхность оболочки является плоскостью, то такую оболочку называют пластиной.
Геометрическая форма объектов, которые могут быть причислены к
оболочкам или пластинам, чрезвычайно разнообразна: в машиностроении — это
корпуса всевозможных машин; в гражданском и промышленном строительстве —
покрытия и перекрытия,навесы, карнизы;
в кораблестроении — корпуса судов, сухих и плавучих доков; в авиастроении —
фюзеляжи и крылья самолетов; в подвижном составе железнодорожного транспорта,
кузова вагонов, цистерны, несущие конструкции локомотивов; в атомной
энергетике — защитная конструкция атомных станций, корпуса реакторов и т.д.
Если срединная
поверхность оболочки образует поверхность вращения в форме цилиндра, то
оболочку называют цилиндрической.
К схеме осесимметричной
цилиндрической оболочки сводится очень много инженерных конструкций, в том
числе: котлов, баков, нефтепроводов, газопроводов, деталей машин и др.
Задача о
расчете тонкостенных оболочек вращения наиболее просто решается в том случае,
когда возможно принять, что напряжения, возникающие в оболочке, постоянны по
толщине и, следовательно, изгиб оболочки отсутствует.
Теория
оболочек, построенная в этом предположении, называется безмоментной теорией оболочек.
Если оболочка
имеет резкий переход и жесткие защемления и, кроме того, нагружена
сосредоточенной силой и моментами, то в местах крепежа оболочки, резких
изменений формы, и в местах действия сосредоточенных сил и моментов возникают
интенсивные напряжения, обусловленные изгибным эффектом. Учет изгибных
эффектов можно получить в рамках моментной теории оболочек.
Следует
отметить, что чем меньше отношение толщины h
оболочки к ее радиусу R, тем точнее выполняется
предположение о постоянстве напряжений по толщине и тем более
точнее выполняются расчеты по безмоментной
теории.
Отметим, что
оболочка считается тонкой, если h/R≤1/20.
Следовательно,
при расчете на прочность тонких оболочек в зависимости от характера
распределения внешних нагрузок, опорных закреплений, применяется или безмоментная или моментная теория. При этом предполагается
При этом предполагается
равномерное распределение напряжений по продольным и поперечным сечениям
оболочек (отсутствие в этих сечениях изгибающих, крутящих моментов и поперечных
сил).
При
осесимметричной нагрузке отсутствуют также сдвигающие силы. Определение усилий
по безмоментной теории производится достаточно точно
на расстоянии, превышающем величину (3÷5)от мест скачкообразного изменения формы или
площади сечения, жестких контурных закреплений или от места приложения внешних
сосредоточенных сил и моментов. Вблизи указанных мест возникают дополнительные
напряжения от изгибного эффекта.
В моментной и безмоментной теории тонких
оболочек или, так называемой технической теории оболочек,состоящей в резком различии их толщины и габаритных размеров, влечет за
собой возможность упрощения теории путем некоторой схематизации действительной
работы конструкций. Эта схематизация формируется в используемых
гипотезах, аналогичных гипотезам в теории стержней, т. е. гипотезам плоских
е. гипотезам плоских
сечений и гипотезам “ненадавливания” слоев оболочки
друг на друга.
Эти гипотезы
позволяют свести трехмерную задачу механики сплошной среды к двумерной, подобно
тому как в теории стержней трехмерная задача сведена к
одномерной.
Далее в
технической теории тонких оболочек пренебрегают членами h/R по сравнению с
единицей.
Оболочки, к
которым применимы упомянутые выше гипотезы, называются тонкими, а те, к
которым эти гипотезы не применимы, называются толстыми.
Граница между
тонкими и толстыми оболочками условны и определяются
отношением h/R≈1/20.
В тех случаях,
когда h/R≥1/20 для получения приемлемых результатов
по точности применяется аппарат механики сплошной среды, в частности теории
упругости или пластичности в зависимости от постановки задачи.
Про алюминиевый провод.
В отличие от меди, алюминий хуже пропускает электрический ток. Для алюминия (провод такого же сечения, что и медный), при токах до 32 А, максимальный ток будет меньше, чем для меди на 20 %. При токах до 80 А алюминий пропускает хуже ток на 30%.
Для алюминия (провод такого же сечения, что и медный), при токах до 32 А, максимальный ток будет меньше, чем для меди на 20 %. При токах до 80 А алюминий пропускает хуже ток на 30%.
Эмпирическое правило для алюминия:
Максимальный ток алюминиевого провода равен площади сечения, умножить на 6.
Имея знания, полученные в данной статье, можно выбрать провод по соотношениям «цена/толщина», «толщина/рабочая температура», а также «толщина/максимальный ток и мощность».
К максимально току в зависимости от площади сечения провода, немцы относятся несколько иначе. Рекомендация по выбору автоматического (защитного) выключателя, расположена в правом столбце.
Таблица зависимости электрического тока защитного автомата (предохранителя) от сечения. Таблица 3.
Вопрос № 5: Можно ли скрыть не выделенные элементы или узлы в системе SCAD Office?
Ответ: Команда фрагментации выделенных узлов и элементов возможна с помощью соответствующих инструментов панели визуализации в программе SCAD. Команда «ножницы» позволяет выделить часть схемы, а команда «подтверждение фрагментации» оставит на экране только отмеченные элементы. В новой версии SCAD Office появилась возможность фрагментировать выделенные узлы и элементы с помощью одноименной команды (иконки находятся в правом нижнем углу). Преимущества второго метода в том, что фрагментации подвергаются элементы и узлы в разных частях схемы.
Команда «ножницы» позволяет выделить часть схемы, а команда «подтверждение фрагментации» оставит на экране только отмеченные элементы. В новой версии SCAD Office появилась возможность фрагментировать выделенные узлы и элементы с помощью одноименной команды (иконки находятся в правом нижнем углу). Преимущества второго метода в том, что фрагментации подвергаются элементы и узлы в разных частях схемы.
В следующей части статьи мы продолжим разбирать вопросы по работе в системе SCAD Office.
Конечные элементы и операции с ними
Прежде всего хотелось бы уделить внимание новым возможностям при работе с объемными элементами. Библиотека конечных элементов пополнилась такими высокоточными объемными элементами, как 10узловая пирамида (тип 38) и 20узловой изопараметрический конечный элемент (тип 37), рис
7.
Рис. 7. 20-узловой изопараметрический
конечный элемент (тип 37)
Появилась возможность выполнять дробление объемных элементов, что значительно облегчает задачу моделирования (рис. 8 и 9).
8 и 9).
Рис. 8. Функция Дробление
объемных элементов
Рис. 9. Дробление объемных элементов
Появилась возможность учета преднапряжения для объемных конечных элементов (рис. 10).
Рис. 10. Функция Преднапряжение
Расширены возможности работы со стержневыми элементами: добавлены операции Дробление стержня полигоном (рис. 11) и Сопряжение стержней (рис. 12).
Рис. 11. Функция Дробление стержней полигоном
Рис. 12. Функция Сопряжение стержней
При этом сопряжение стержней может быть выполнено под углом либо сопрягаться дугой окружности (рис. 13).
Рис. 13. Окно функции Сопряжение стержней
Операция Объединение стержневых элементов расширена возможностью объединения в один элемент нескольких стержней, лежащих на одной прямой и связанных между собой (рис. 14).
Рис. 14. Функция Объединение двух стержневых элементов
Реализованы новые функции и для работы с пластинчатыми элементами. Если ранее жесткие вставки можно было вводить только в стержневые элементы, то теперь добавлена возможность задавать смещение срединной плоскости (жесткой вставки) в пластинчатых элементах (рис. 15).
Если ранее жесткие вставки можно было вводить только в стержневые элементы, то теперь добавлена возможность задавать смещение срединной плоскости (жесткой вставки) в пластинчатых элементах (рис. 15).
Рис. 15. Окно функции Смещение срединной плоскости пластин
Кроме того, добавлена операция дробления пластин с учетом промежуточных узлов, находящихся в границах пластин (рис. 16).
Рис. 16. Функция Дробление пластин с учетом промежуточных узлов
S=0,8D.
Небольшая поправка — является округленным коэффициентом. Точная расчетная формула:
В электропроводке и электромонтаже в 90 % случаях применяется медный провод. Медный провод по сравнению с алюминиевым проводом, имеет ряд преимуществ. Он более удобен в монтаже, при такой же силе токе имеет меньшую толщину, более долговечен. Но чем больше диаметр (площадь сечения), тем выше цена медного провода. Поэтому, несмотря на все преимущества, если сила тока превышает значение 50 Ампер, чаще всего используют алюминиевый провод. В конкретном случае используется провод, имеющий алюминиевую жилу 10 мм и более.
В конкретном случае используется провод, имеющий алюминиевую жилу 10 мм и более.
В квадратных миллиметрах измеряют площадь сечения проводов. Наиболее чаще всего на практике (в бытовой электрике), встречаются такие площади сечения: 0,75; 1,5; 2,5; 4 мм .
Существует иная система измерения площади сечения (толщины провода) — система AWG, которая используется, в основном в США. Ниже приведена таблица сечений проводов по системе AWG, а так же перевод из AWG в мм .
Выделяют, три основные принципа, при выборе сечения провода.
1. Для прохождения электрического тока, площадь сечения провода (толщина провода), должна быть достаточной. Понятие достаточно означает, что когда проходит максимально возможный, в данном случае, электрический ток, нагрев провода будет допустимый (не более 600С).
2. Достаточное сечение провода, что бы падение напряжения не превышало допустимого значения. В основном это относится к длинным кабельным линиям (десятки, сотни метров) и токам большой величины.
3. Поперечное сечение провода, а также его защитная изоляция, должна обеспечивать механическую прочность и надежность.
Для питания, например люстры, используют в основном лампочки с суммарной потребляемой мощностью 100 Вт (ток чуть более 0,5 А).
Выбирая толщину провода, необходимо ориентироваться на максимальную рабочую температуру. Если температура будет превышена, провод и изоляция на нем будут плавиться и соответственно это приведет к разрушению самого провода. Максимальный рабочий ток для провода с определенным сечением ограничивается только максимально его рабочей температурой. И временем, которое сможет проработать провод в таких условиях.
Далее приведена таблица сечения проводов, при помощи которой в зависимости от силы тока, можно подобрать площадь сечения медных проводов. Исходные данные – площадь сечения проводника.
Максимальный ток для разной толщины медных проводов. Таблица 1.
Сечение токопроводящей жилы, мм2 | Ток, А, для проводов, проложенных | ||
открыто | в одной трубе | ||
одного двух жильного | одного трех жильного | ||
0,5 | 11 | — | — |
0,75 | 15 | — | — |
1 | 17 | 15 | 14 |
1,2 | 20 | 16 | 14,5 |
1,5 | 23 | 18 | 15 |
2 | 26 | 23 | 19 |
2,5 | 30 | 25 | 21 |
3 | 34 | 28 | 24 |
4 | 41 | 32 | 27 |
5 | 46 | 37 | 31 |
6 | 50 | 40 | 34 |
8 | 62 | 48 | 43 |
10 | 80 | 55 | 50 |
16 | 100 | 80 | 70 |
25 | 140 | 100 | 85 |
35 | 170 | 125 | 100 |
50 | 215 | 160 | 135 |
70 | 270 | 195 | 175 |
95 | 330 | 245 | 215 |
120 | 385 | 295 | 250 |
Выделены номиналы проводов, которые используются в электрике. «Один двужильный» — провод, имеющий два провода. Один Фаза, второй – Ноль – это считается однофазное питание нагрузки. «Один трехжильный» — используется при трехфазном питании нагрузки.
«Один двужильный» — провод, имеющий два провода. Один Фаза, второй – Ноль – это считается однофазное питание нагрузки. «Один трехжильный» — используется при трехфазном питании нагрузки.
Таблица помогает определиться, при каких токах, а также в каких условиях эксплуатируется провод данного сечения.
Например, если на розетке написано «Мах 16А», то к одной розетке можно проложить провод сечением 1,5мм . Необходимо защитить розетку выключателем на ток не более чем 16А, лучше даже 13А, или 10 А. Эту тему раскрывает статья «Про замену и выбор защитного автомата».
Из данных таблицы видно, что одножильный провод – означает, что вблизи (на расстоянии менее 5 диаметров провода), не проходит более никаких проводов. Когда два провода рядом, как правило, в одной общей изоляции – провод двужильный. Здесь более тяжелый тепловой режим, поэтому меньше максимальный ток. Чем больше собрано в проводе или пучке проводов, тем меньше должен быть максимальный ток отдельно для каждого проводника, из-за возможности перегрева.
Однако, эта таблица не совсем удобна с практической стороны. Зачастую исходный параметр – это мощность потребителя электроэнергии, а не электрический ток. Следовательно, нужно выбирать провод.
Определяем ток, имея значение мощности. Для этого, мощность Р (Вт) делим на напряжение (В) – получаем ток (А):
Пример расчета элемента тонкостенной оболочки вращения
Рассчитать
коническую часть тонкостенной оболочки вращения (рис.8.13) с толщиной стенки
δ = 0,02 м. Давление внутри оболочки P= 0,2 МПа, удельный вес жидкости γ
= 1,5∙104 н/м3.
Рис.8.13
Решение:
Рассмотрим
отсеченную часть с действующими на нее силовыми факторами (см. рис.8.4).
Проводим через
точку А
первое сечение.
;
;
;
.
Второе сечение
проводим на расстоянии x= 0,15 м.
Высота столба
жидкости над сечением v= 10 —
0,15 = 9,85 м.
Давление .
В соответствии
с уравнением равновесия нижней отсеченной части оболочки (8. 13) имеем
13) имеем
В соответствии
с уравнением Лапласаимеем,
Радиус
кривизны R2 для конуса равен ∞
Третье сечение
проведем через точку В(x=
0,25 м).
Высота столба
жидкости над сечением v= 10 —
0,25 = 9,75 м.
Давление .
Решая
уравнение равновесия (8.16) имеем
В соответствии
с уравнением Лапласа имеем,
Радиус
кривизны R2 для конуса равен ∞
Пример построения расчета МКИ в SCAD
Построение моделей расчета методом конечных элементов не обходится без приложения нагрузок, вычисленные вручную значения присваиваются в расчетных программах МКЭ на элемент. Помощь в сборе ветровых и снеговых нагрузках инженеру окажет программа ВЕСТ. Программа включает в себя несколько расчетных модулей, позволяющих по введенном району строительства и очертанием контура здания вычисляет ветровую и снеговую нагрузку (самые распространенные расчетные модули программы ВЕСТ).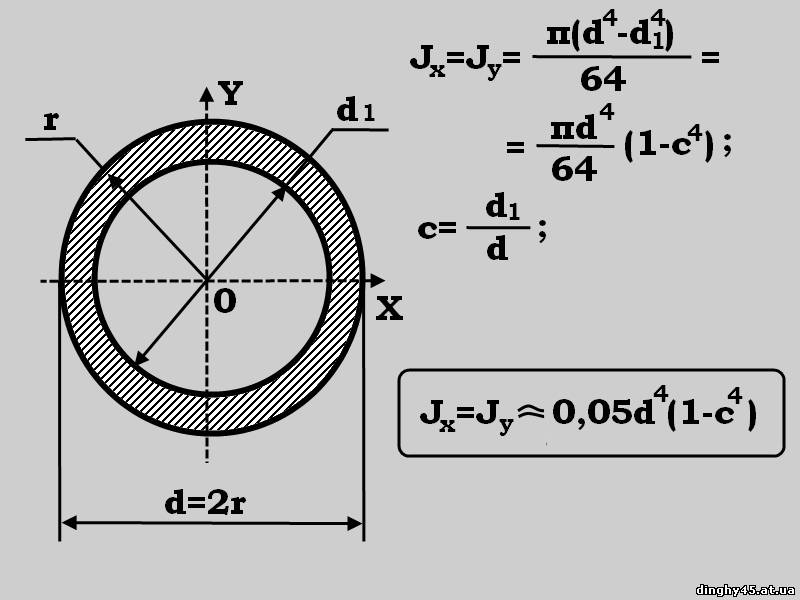 Так, при расчете навеса, конструктор должен указать высоту конька, угол наклона и ширину ската. По полученным эпюрам нагрузка вводится в расчетную программу, например, ПК ЛИРА 10.4.
Так, при расчете навеса, конструктор должен указать высоту конька, угол наклона и ширину ската. По полученным эпюрам нагрузка вводится в расчетную программу, например, ПК ЛИРА 10.4.
В качестве вывода, могу сказать, что программный комплекс SCAD и его сателлиты позволяют пользователю существенно снизить трудозатраты при вычислении локальных задач, а также формировать точные расчетные модели, а также содержат справочные данные, необходимые в работе инженеров — строителей. Автономность программ позволяет конструкторам использовать их в сочетании с любыми расчетными комплексами, основанных на расчете методом конечных элементов.
Также рекомендую посмотреть вебинар по совместному использованию ПК ЛИРА 10 и программы ЗАПРОС (SCAD office) на примере расчета свайного основания.
Пример расчета толстостенной стальной трубы
Для
толстостенной стальной трубы, имеющей внутренний диаметр d = 0,03 м и наружный диаметр D = 0,18 м, и изготовленной из пластичного материала
с σT = 250 МПа
и с коэффициентом Пуассона μ = 0,5,
требуется:
1. Определить
Определить
давление pT,
при котором в материале трубы начнется пластическое деформирование;
2. Определить
предельное внутреннее давление pПР, при котором весь материал будет находиться в
пластическом состоянии;
3. Построить
эпюры распределения напряжений σp, σφ,
σz по толщине стенки для двух
состояний трубы, рассмотрены в п. 1 и 2;
4. Определить
допускаемое значение давления pa = pДОП при коэффициенте
запаса прочности n = 1,5.
Решение.
1. По
формуле определяем давление, при котором на внутренней
поверхности трубы появятся пластические деформации:
2. С
учетом того, что pa = pT, из формул
определяем
напряжения, соответствующие началу пластического течения:
Данные для
числовых расчетов сводим в таблицу
1,5 | 148,5 | -140,5 |
3 | 40,1 | -32 |
6 | 13,0 | -5,0 |
9,5 | 8,0 |
Эпюры
напряжений σp, σφ, σz
для упругого состояния материала трубы приведены на рис. 1, а.
1, а.
Рассмотрим
теперь предельное состояние трубы, когда весь материал трубы находится в
пластическом состоянии. Предельное давление в этом случае определяется по
формуле
Рис.1
3. Для
определения напряжений σp, σφ,
σz воспользуемся формулами
Данные для
числовых расчетов сводим в таблицу
1,5 | -517,8 | -228,9 | -373,4 |
3 | -317,6 | -28,6 | -173,1 |
6 | -117,5 | -171,7 | 27,2 |
9 | 289,0 | 144,5 |
Для более
точного построения эпюр и определим точки, в которых указанные
напряжения равны нулю:
для эпюры
для эпюры
4. Эпюры
Эпюры
напряжений σp, σφ, σz
приведены на рис. 1, б.
Допускаемое значение внутреннего давления определяется из условия pДОП = pПР/n pДОП = 517,8/1,5 = 345,2
МПа.
Пример 3.
Для стальной
составной трубы (рис. 1) заданы: внутренний радиус внутренней трубы а = 7см, внутреннее давление р = 100 МПа, расчетное сопротивление
стали Ry= 240 МПа, коэффициент Пуассона ν = 0,3; модуль продольной
упругости Е= 2∙105 МПа.
Требуется:
1) определить
внешний радиус внутренней трубы b,
внешний радиус наружной трубы с,
радиальный натяг δ;
2) проверить
прочность сплошной трубы с внутренним радиусом а и внешним радиусом с,
нагруженной внутренним давлением р, используя III теорию прочности;
3) проверить
прочность в опасных точках составнойтрубы, нагруженной внутренним давлением р, используя IIIтеорию
прочности;
4) определить
радиальные перемещения точек внутреннего канала.
Рис.1
Решение.
1) Определение
геометрических параметров b, c и δ.
Внешний радиус
с наружной трубы определяется на
основе условия прочности:
Внешний радиус
b внутренней трубы определяется по формуле:
Радиальный
натяг рассчитываем по формуле:
2) Проверка прочности сплошной трубы с внутренним радиусом а и внешним радиусом с, нагруженной давлением р.
Из теории
расчета толстостенных труб известно, что и при нагружении
внутренним давлением, и при нагружении внешним
давлением опасными являются точки на внутреннем канале трубы.
Рассчитываем
напряжения в точках 1 (рис. 1),
используя формулы
и полагая в
нихb = c, pa = p, pb = 0, r = a:
По аналогии
определяем в точках 2 и 3:
и в точке 4:
Эпюра
распределения напряжений по толщине сплошной трубы с внутренним радиусом a и внешним радиусом c показана на рис.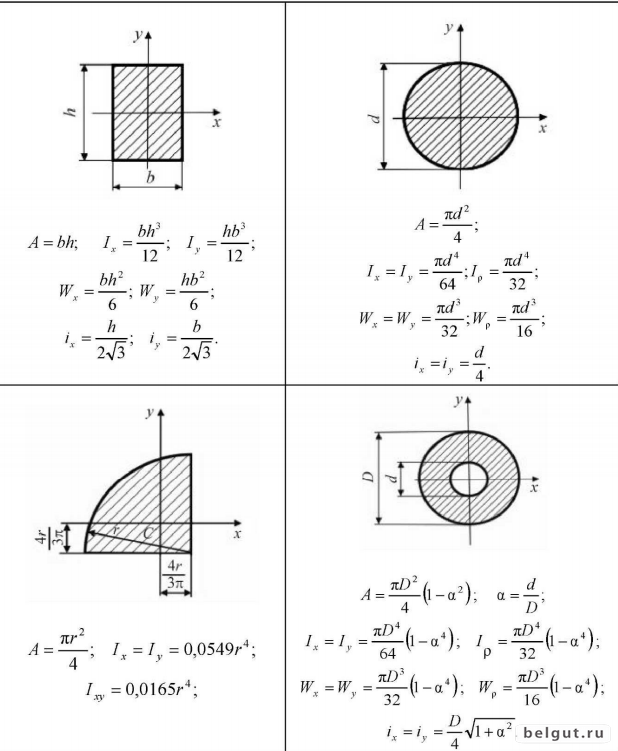 2.
2.
Рис.2
Условие
прочности по III теории
прочности имеет вид
В нашем случае
в точке 1 трубы будет
Таким образом,
получаем
Условие
прочности для сплошной трубы не выполняется.
3) Проверка
прочности в опасных точках составнойтрубы, нагруженной внутренним давлениемр.
Вначале
рассчитываем давление от натяга рк на поверхности контакта наружной и внутренней
трубы, используя формулу
Рассчитываем
напряжения и в точке 1
от действия натяга рк,
используя формулы
и полагая в
них pa = 0, pb = pk, r =a:
Рассчитаем
суммарные напряжения и в точке 1
от действия р
и pk:
Проверяем
прочность составной трубы в точке 1
по IIIтеории прочности:
Условие
прочности для составной трубы выполняется.
4) Определение
радиальных перемещений точек 1
составной трубы.
Воспользуемся
законом Гука для двухосного напряженного состояния
Особенности электрических проводов
Наиболее широкое применение находят марки проводов ПУHП и ПУГHП, а также ВПП, ПHCB и PKГM, которые обладают следующими, очень важными для получения безопасного подключения основными техническими характеристиками:
- ПУНП — плоское проводное изделие установочного или так называемого монтажного типа, с однопроволочными жилами из меди в ПВХ-изоляции. Такая разновидность отличается количеством жил, а также номинальным напряжением в пределах 250 В с частотой 50 Гц и температурным эксплуатационным режимом от минус 15 °C до плюс 50 °C;
- ПУГНП — гибкая разновидность с многопроволочными жилами. Основные показатели, которые представлены номинальным уровнем напряжения, частотой и температурным эксплуатационным режимом, не отличаются от аналогичных данных ПУHП;
- AПB — алюминиевая одножильная разновидность, круглый провод, имеющий защитную ПВХ-изоляцию и однопроволочную или многопроволочную жилу.
 Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C;
Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C; - ПBC — многожильная медная разновидность с ПBX-изоляцией, придающей проводу высокие показатели плотности и традиционную округлую форму. Термоустойчивая жила рассчитана для номинального уровня 380 В при частоте 50 Гц;
- PKГM — силовая монтажная разновидность, представленная одножильным медным проводом с кремнийорганической резиновой или стекловолоконной изоляцией, пропитанной термостойким составом. Температурный эксплуатационный режим составляет от минус 60 °C до плюс 180 °C;
- ПHCB — нагревательная одножильная разновидность в виде однопроволочного провода на основе оцинкованной или вороненой стали. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 80 °C;
- ВПП — одножильная медная разновидность с многопроволочной жилой и изоляцией на основе ПBX или полиэтилена.
 Температурный эксплуатационный режим составляет от минус 40 °C до плюс 80 °C.
Температурный эксплуатационный режим составляет от минус 40 °C до плюс 80 °C.
В условиях невысокой мощности применяется медный провод ШBBП с защитной внешней ПBX-изоляцией. Многопроволочного типа жила обладает прекрасными показателями гибкости, а само проводное изделие рассчитано максимум на 380 В, при частоте в пределах 50 Гц.
Проводные изделия самых распространенных типов реализуются в бухтах, и чаще всего имеют белое окрашивание изоляции.
Вопрос 22: Как следует анализировать результаты расчета здания на пульсационную составляющую ветрового воздействия?
Ответ:
Для начала необходимо проанализировать частоты полученных форм колебаний. Для этого смотрим в разделе «Перемещения — Частоты и периоды колебаний» значения полученных частот собственных колебаний здания. Согласно СП «Нагрузки и воздействия» необходимо учитывать формы колебаний, ниже предельного значения, указанного в нормах. Таким образом, Вы должны увидеть в появившемся окне форм колебаний, частоту выше предельного значения, если частота ниже, то необходимо увеличить количество форм колебаний. Дальнейший учет форм колебаний происходит автоматически: программа согласно требованиям норм суммирует полученные усилия по каждой форме колебаний и добавляет их в РСУ. Пользователь SCAD может анализировать отдельно усилия по пульсационной или средней составляющей ветрового воздействия. Выбрать нужный пункт можно в выпадающем окне текущего загружения.
Дальнейший учет форм колебаний происходит автоматически: программа согласно требованиям норм суммирует полученные усилия по каждой форме колебаний и добавляет их в РСУ. Пользователь SCAD может анализировать отдельно усилия по пульсационной или средней составляющей ветрового воздействия. Выбрать нужный пункт можно в выпадающем окне текущего загружения.
Вопрос 20: Как в SCAD создать объемные тела?
Ответ:
Создавать объемные тела в SCAD возможно способом выдавливание объемных тел из пластин. Необходимая для этой процедуры команда называется «Копирование схемы». Для начала выделяем ранее созданные пластины, и жмем команду «Копирование схемы». В появившемся окне задаем шаг и количество шагов копирования. Шаг выбирайте соизмеримый с шагом триангуляции плиты, так не получиться у Вас вытянутых объёмных элементов. Количество шагов выбирайте исходя из габаритных размеров создаваемого тела
Перед обращением к команде «Копирование схемы» пластинчатые элементы необходимо выделить! Это важно!
Нюансом здесь является то, что программа при использовании команды «Копирование схемы» работает и с невыделенными элементами, копируя их по указанным параметрам. В таком случае необходимо разделять конструкции на подсхему, соединив их потом в «Режиме сборки».
В таком случае необходимо разделять конструкции на подсхему, соединив их потом в «Режиме сборки».
Список источников
- blog.infars.ru
- sapr.ru
- www.soprotmat.ru
- www.calc.ru
- proprovoda.ru
Поделитесь с друзьями!
Поперечное сечение проводника как важнейший критерий выбора провода
Классификация любых электрических проводов включает в себя основные параметры, представленные проводимостью, площадью поперечного сечения или диаметром, материалами, из которых изготовлен проводник, типовыми особенностями изоляционной защиты, уровнем гибкости, а также показателями тепловой стойкости.
Площадь или поперечное сечение проводника — один из наиболее важных критериев выбора провода.
Особенности электрических проводов
Наиболее широкое применение находят марки проводов ПУHП и ПУГHП, а также ВПП, ПHCB и PKГM, которые обладают следующими, очень важными для получения безопасного подключения основными техническими характеристиками:
- ПУНП — плоское проводное изделие установочного или так называемого монтажного типа, с однопроволочными жилами из меди в ПВХ-изоляции. Такая разновидность отличается количеством жил, а также номинальным напряжением в пределах 250 В с частотой 50 Гц и температурным эксплуатационным режимом от минус 15 °C до плюс 50 °C;
- ПУГНП — гибкая разновидность с многопроволочными жилами. Основные показатели, которые представлены номинальным уровнем напряжения, частотой и температурным эксплуатационным режимом, не отличаются от аналогичных данных ПУHП;
- AПB — алюминиевая одножильная разновидность, круглый провод, имеющий защитную ПВХ-изоляцию и однопроволочную или многопроволочную жилу.
 Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C;
Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C; - ПBC — многожильная медная разновидность с ПBX-изоляцией, придающей проводу высокие показатели плотности и традиционную округлую форму. Термоустойчивая жила рассчитана для номинального уровня 380 В при частоте 50 Гц;
- PKГM — силовая монтажная разновидность, представленная одножильным медным проводом с кремнийорганической резиновой или стекловолоконной изоляцией, пропитанной термостойким составом. Температурный эксплуатационный режим составляет от минус 60 °C до плюс 180 °C;
- ПHCB — нагревательная одножильная разновидность в виде однопроволочного провода на основе оцинкованной или вороненой стали. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 80 °C;
- ВПП — одножильная медная разновидность с многопроволочной жилой и изоляцией на основе ПBX или полиэтилена.
 Температурный эксплуатационный режим составляет от минус 40 °C до плюс 80 °C.
Температурный эксплуатационный режим составляет от минус 40 °C до плюс 80 °C.
В условиях невысокой мощности применяется медный провод ШBBП с защитной внешней ПBX-изоляцией. Многопроволочного типа жила обладает прекрасными показателями гибкости, а само проводное изделие рассчитано максимум на 380 В, при частоте в пределах 50 Гц.
Проводные изделия самых распространенных типов реализуются в бухтах, и чаще всего имеют белое окрашивание изоляции.
Площадь поперечного сечения проводника
В последние годы отмечается заметное понижение качественных характеристик изготавливаемой кабельной продукции, в результате чего страдают показатели сопротивления — сечение проводов. Диаметр любого проводника в обязательном порядке должен обладать соответствием всем заявленным производителем параметрам.
Любое отклонение, составляющее даже 15-20 %, может стать причиной значительного перегрева электрической проводки или оплавления изоляционного материала, поэтому выбору площади или толщины проводника нужно уделять повышенное внимание не только на практике, но и с точки зрения теории.
Поперечное сечение проводников
Параметры, наиболее важные для правильного выбора сечения проводника, отражены в следующих рекомендациях:
- толщина проводника — достаточная для беспрепятственного прохождения электротока, при максимально возможном нагреве провода в пределах 60 °C;
- сечение проводника — достаточное для резкого понижения напряжения, не превышающего допустимые показатели, что особенно важно для очень длинной электропроводки и значительных токов.
Особое внимание требуется уделять максимальным показателям рабочего температурного режима, при превышении которого проводник и защитная изоляция приходят в негодность.
Сечением используемого проводника и его защитной изоляцией должна в обязательном порядке обеспечиваться полноценная механическая прочность и надежность электрической проводки.
Формула поперечного сечения проводника
Как правило, провода обладают круглым сечением, но допустимые токовые показатели должны рассчитываться согласно площади поперечного сечения. С целью самостоятельного определения площади сечения в одножильном или многожильном проводе осторожно вскрывается оболочка, представляющая собой изоляцию, после чего в одножильном проводнике замеряется диаметр.
С целью самостоятельного определения площади сечения в одножильном или многожильном проводе осторожно вскрывается оболочка, представляющая собой изоляцию, после чего в одножильном проводнике замеряется диаметр.
Площадь определяется в соответствии с хорошо известной даже школьникам физической формулой:
S = π х D²/4 или S = 0,8 х D², где:
- S является площадью сечения в мм2;
- π — число π, стандартная величина, равная 3,14;
- D является диаметром в мм.
Проводник
Замеры многожильного провода потребуют его предварительного распушения, а также последующего подсчета количества всех жилок внутри пучка. Затем измеряется диаметр одного составляющего элемента и вычисляется площадь сечения в соответствии со стандартной формулой, указанной выше. На заключительном этапе замеров суммируются площади жилок с целью определения показателей их общего сечения.
С целью определения диаметра проводной жилы используется микрометр или штангенциркуль, но при необходимости можно воспользоваться стандартной ученической линейкой или сантиметром. Замеряемую жилку провода нужно максимально плотно намотать на палочку двумя десятками витков. При помощи линейки или сантиметра требуется замерить расстояние намотки в мм, после чего показатели используются в формуле:
Замеряемую жилку провода нужно максимально плотно намотать на палочку двумя десятками витков. При помощи линейки или сантиметра требуется замерить расстояние намотки в мм, после чего показатели используются в формуле:
D = l/n,
Где:
- l представлено расстоянием намотки жилки в мм;
- n является числом витков.
Следует отметить, что большее сечение провода позволяет обеспечивать запас по показателям тока, в результате чего уровень нагрузки на электропроводку можно незначительно превышать.
Чтобы самостоятельно определить проводное сечение монолитной жилы, требуется посредством обычного штангенциркуля или микрометра выполнить замеры диаметра внутренней части кабеля без защитной изоляции.
Таблица соответствия диаметров проводов и площади их сечения
Определение кабельного или проводного сечения по стандартной физической формуле относится к числу достаточно трудоемких и сложных процессов, не гарантирующих получение максимально точной результативности, поэтому целесообразно использовать с этой целью специальные, уже готовые табличные данные.
| Диаметр кабельной жилы | Показатели сечения | Проводники с жилой медного типа | ||
| Мощность в условиях сети 220 В | Ток | Мощность в условиях сети 380 В | ||
| 1,12 мм | 1,0 мм2 | 3,0 кВт | 14 А | 5,3 кВт |
| 1,38 мм | 1,5 мм2 | 3,3 кВт | 15 А | 5,7 кВт |
| 1,59 мм | 2,0 мм2 | 4,1 кВт | 19 А | 7,2 кВт |
| 1,78 мм | 2,5 мм2 | 4,6 кВт | 21 А | 7,9 кВт |
| 2,26 мм | 4,0 мм2 | 5,9 кВт | 27 А | 10,0 кВт |
| 2,76 мм | 6,0 мм2 | 7,7 кВт | 34 А | 12,0 кВт |
| 3,57 мм | 10,0 мм2 | 11,0 кВт | 50 А | 19,0 кВт |
| 4,51 мм | 16,0 мм2 | 17,0 кВт | 80 А | 30,0 кВт |
| 5,64 мм | 25,0 мм2 | 22,0 кВт | 100 А | 38,0 кВт |
| 6,68 мм | 35,0 мм2 | 29,0 кВт | 135 А | 51,0 кВт |
Как определить сечение многожильного провода?
Многожильные провода также известны под названием многопроволочных или гибких кабелей, которые представляют собой плотно свитые в один пучок проволочники одножильного типа.
Чтобы самостоятельно грамотно произвести вычисление сечения или площади многожильных проводов, необходимо изначально рассчитать сечение каждой проволочки в пучке, после чего полученный результат умножить на их общее количество.
Заключение
Сечение проводов или кабелей по токовым показателям и уровню мощности является одним из наиважнейших параметров электрической проводки. Самостоятельное определение диаметра выполняется несколькими доступными способами. Сечение проводника может быть рассчитано в соответствии с несложной формулой или выбрано по стандартным табличным данным.
Видео на тему
понятие, площадь, формула и таблица соответствия диаметру
На чтение 9 мин. Просмотров 2.8k. Опубликовано
Обновлено
Для правильного выбора и организации электролинии необходимо учитывать параметры и нагрузку проводников. Они представляют собой металлическую нить из меди, алюминия, стали, цинка, титана, никеля и обеспечивают передачу тока от его источника до потребителя. У проводников есть поперечное сечение – это фигура, образованная от их рассечения плоскостью поперечного направления. Если его подобрать неправильно, линия выйдет из строя или загорится при скачках напряжения.
Площадь поперечного сечения как электротехническая величина
От поперечного сечения зависит токопроводимость провода
В качестве примера сечения можно рассмотреть распил изделия под углом 90 градусов относительно поперечной оси. Контур фигуры, получившейся в результате, определяется конфигурацией объекта. Кабель имеет вид небольшой трубы, поэтому при распиле выйдет фигура в виде двух окружностей определенной толщины. При поперечном рассечении круглого металлического прута получится форма круга.
В электротехнике площадь ПС будет значить прямоугольное сечение проводника в отношении к его продольной части. Сечение жил всегда будет круглым. Измерение параметра осуществляется в мм2.
Начинающие электрики могут перепутать диаметр и сечение элементов. Чтобы определить, какая площадь сечения у жилы, понадобиться учесть его круглую форму и воспользоваться формулой:
S = πхR2, где:
- S – площадь круга;
- π — постоянная величина 3,14;
- R – радиус круга.
Если известен показатель площади, легко найти удельное сопротивление материала изготовления и длину провода. Далее вычисляется сопротивление тока.
Для удобства расчетов начальная формула преобразуется:
- Радиус – это ½ диаметра.
- Для вычисления площади π умножается на D (диаметр), разделенный на 4, или 0,8 умножается на 2 диаметра.
При вычислениях используют показатель диаметра, поскольку его неправильный подбор может вызвать перегрев и воспламенение кабеля.
Цели расчета
Поперечное сечение проводов для освещения
Рассчитывать параметры площади сечения проводника необходимо с несколькими целями:
- получение необходимого количества электричества для запитки бытовых приборов;
- исключение переплат за неиспользуемый энергоноситель;
- безопасность проводки и предотвращение возгораний;
- возможность подключения высокомощной техники к сети;
- предотвращение оплавления изоляционного слоя и коротких замыканий;
- правильная организация осветительной системы.
Оптимальное сечение провода для освещения – 1,5 мм2 для линии, 4-6 мм2 на вводе.
Соотношение диаметра кабеля с площадью его сечения
Определение посредством формулы площади поперечного сечения проводников занимает длительное время. В некоторых случаях уместно использовать данные из таблицы. Поскольку для организации современной проводки применяется медный кабель, в таблицу вносятся параметры:
- диаметр;
- сечение в соответствии с показателем диаметра;
- предельная мощность нагрузки проводников в сетях с напряжением 220 и 380 В.
| Диаметр жилы, мм | Параметры сечения, мм2 | Сила тока, А | Мощность медного проводника, кВт | |
| Сеть 220 В | Сеть 380 В | |||
| 1,12 | 1 | 14 | 3 | 5,3 |
| 1,38 | 1,5 | 15 | 3,3 | 5,7 |
| 1,59 | 2 | 19 | 4,1 | 7,2 |
| 1,78 | 2,5 | 21 | 4,6 | 7,9 |
| 2,26 | 4 | 27 | 5,9 | 10 |
| 2,76 | 6 | 34 | 7,7 | 12 |
| 3,57 | 10 | 50 | 11 | 19 |
Посмотрев данные в соответствующих колонках, можно узнать нужные параметры для электролинии жилого здания или производственного объекта.
Расчет сечения многожильного проводника
Многожильный провод представляет собой несколько отдельных жил. Расчет его сечения осуществляется следующим образом:
- Находится показатель площади сечения у одной жилы.
- Пересчитываются кабельные жилы.
- Количество умножается на поперечное сечение одной жилы.
При подключении многожильного проводника его концы обжимаются специальной гильзой с использованием обжимных клещей.
Особенности самостоятельного расчета
Самостоятельное вычисление продольного сечения выполняется на жиле без изоляционного покрытия. Кусочек изоляции можно отодвинуть или снять на отрезке, приобретенном специально для тестирования. Вначале понадобится определить диаметр и по нему найти сечение. Для работ используется несколько методик.
При помощи штангенциркуля
Способ оправдан, если будут измеряться параметры усеченного, или бракованного кабеля. К примеру, ВВГ может обозначаться как 3х2,5, но фактически быть 3х21. Вычисления производятся так:
- С проводника снимается изоляционное покрытие.
- Диаметр замеряется штангенциркулем. Понадобится расположить провод между ножками инструмента и посмотреть на обозначения шкалы. Целая величина находится сверху, десятичная – снизу.
- На основании формулы поиска площади круга S = π (D/2)2 или ее упрощенного варианта S = 0,8 D² определяется поперечное сечение.
- Диаметр равен 1,78 мм. Подставляя величину в выражение и округлив результат до сотых, получается 2,79 мм2.
Для бытовых целей понадобятся проводники с сечением 0,75; 1,5; 2,5 и 4 мм2.
С использованием линейки и карандаша
Вычисление ПС с помощью линейки и карандаша
При отсутствии специального измерителя можно воспользоваться карандашом и линейкой. Операции выполняются с тестовым образом:
- Зачищается от изоляционного слоя участок, равный 5-10 см.
- Получившаяся проволока наматывается на карандаш. Полные витки укладываются плотно, пространства между ними быть не должно, «хвостики» направляются вверх или вниз.
- В конечном итоге должно получиться определенное число витков, их требуется посчитать.
- Намотка прикладывается к линейке так, чтобы нулевое деление совпадало с первой намоткой.
- Замеряется длина отрезка и делится на количество витков. Получившаяся величина – диаметр.
- Например, получилось 11 витков, которые занимают 7,5 мм. При делении 7,5 на 11 выходит 0,68 мм – диаметр кабеля. Сечение можно найти по формуле.
Точность вычислений определяется плотностью и длиной намотки.
Таблица соответствия диаметра проводов и площади их сечения
Если нет возможности пройти тестирование диаметра или сделать вычисление при покупке, допускается использовать таблицу. Данные можно сфотографировать, распечатать или переписать, а затем применять, чтобы найти нормативный или популярный размер жилы.
| Диаметр кабеля, мм | Сечение проводника, мм2 |
| 0,8 | 0,5 |
| 0,98 | 0,75 |
| 1,13 | 1 |
| 1,38 | 1,5 |
| 1,6 | 2 |
| 1,78 | 2,5 |
| 2,26 | 4 |
| 2,76 | 6 |
| 3,57 | 10 |
При покупке электрокабеля понадобится посмотреть параметры на этикетке. К примеру, используется ВВНГ 2х4. Количество жил – величина после «х». То есть, изделие состоит из двух элементов с поперечным сечением 4 мм2. На основании таблицы можно проверить точность информации.
Чаще всего диаметр кабеля меньше, чем заявлен на упаковке. У пользователя два варианта – применять другой или выбрать с большей площадью сечения кабель по диаметру. Выбрав второй, понадобится проверить изоляцию. Если она не сплошная, тонкая, разная по толщине, остановитесь на продукции другого изготовителя.
Определение сечения проводника на вводе
Уточнить номинальные показатели можно в компании Энергосбыта или документации к товару. К примеру, номинал автомата на вводе составляет 25 А, мощность потребления – 5 кВт, сеть однофазная, на 220 В.
Подбор сечения осуществляется так, чтобы допустимый ток жил за длительный период был больше номинала автомата. Например, в доме на ввод пущен медный трехжильный проводник ВВГнг, уложенный открытым способом. Оптимальное сечение – 4 мм2, поэтому понадобится материал ВВГнг 3х4.
После этого высчитывается показатель условного тока отключения для автомата с номиналом 25 А: 1,45х25=36,25 А. У кабеля с площадью сечения 4 мм2 параметры длительно допустимого тока 35 А, условного – 36,25 А. В данном случае лучше взять вводный проводник из меди сечением 6 мм2 и допустимым предельным током 42 А.
Вычисление сечения провода для линии розеток
Сечение кабелей для домашних электроустановок
Каждый электроприбор имеет показатели собственной мощности. Они замеряются в Ваттах и указываются в паспорте либо на наклейке на корпусе. Примером поиска сечения будет линия запитки для стиральной машины мощностью 2,4 кВт. При расчетах учитывается:
- материал провода и способ укладки – трехжильный ВВГнг-кабель из меди, спрятанный в стене;
- особенности сечения – оптимальная величина составляет 1,5 мм2, т.е. понадобится кабель 3х1,5;
- использование розетки. Если подключается только машинка-автомат, характеристик будет достаточно;
- система защиты – автомат, номинальный ток которого 10 А.
Для двойных розеток применяется кабель из меди с сечением 2,5 мм2 и автомат номиналом 16 А.
Подбор сечения для трехфазной линии 380 В с несколькими приборами
Подключение нескольких видов бытовой техники к трехфазной линии предусматривает протекание потребляемого тока по трем жилам. В каждом из них будет меньшая величина, чем в двухжильном. На основании данного явления в трехфазной сети допускается применять кабель с меньшим сечением.
К примеру, в доме устанавливается генератор с мощностью 20 кВт и суммарной мощностью по трем фазам 52 А. На основании значений таблицы выйдет, что оптимальное сечение кабеля – 8,4 мм2. На основании формулы высчитывается фактическое сечение: 8,4/1,75=4,8 мм2. Чтобы подсоединить генератор мощностью 20 кВт на трехфазную сеть 380 В необходим медный проводник, сечение каждой жилы которого 4,8 мм2.
Сечение проводов в домах старой застройки и предельная нагрузка
В многоэтажках советского периода используется алюминиевая проводка. С учетом правильного соединения узлов в распредкоробе, качества изоляции и надежности контактов соединения она прослужит от 10 до 30 лет.
При необходимости подключения техники с большой энергоемкостью в домах с проводкой из алюминия на основе мощности потребления подбирается сечение и диаметр жил. Все данные указаны в таблице.
| Ток, А | Максимальная мощность, ВА | Диаметр кабеля, мм | Сечение кабеля, мм2 |
| 14 | 3000 | 1,6 | 2 |
| 16 | 3500 | 1,8 | 2,5 |
| 18 | 4000 | 2 | 3 |
| 21 | 4600 | 2,3 | 4 |
| 24 | 5300 | 2,5 | 5 |
| 26 | 5700 | 2,7 | 6 |
| 31 | 6800 | 3,2 | 8 |
| 38 | 8400 | 3,6 | 10 |
Какой кабель выбрать для квартирной проводки
Несмотря на дешевизну алюминиевых проводников, от их применения лучше отказаться. Причина – низкая надежность контактов, через которые будут проходить токи. Второй повод – несоответствие сечения провода мощности современной бытовой техники. Кабель из меди отличается надежностью, длительным сроком эксплуатации.
В квартирах и домах допускается использовать провод с маркировкой:
При выборе количества жил понадобится учесть способность токопроводимости на единицу сечения. В данном случае квартирную сеть лучше сделать из одножильного провода, толщина которого больше. Многожильные элементы можно изгибать многократно, подсоединять на них электроприборы. Качественным будет только кабель с тонкими жилами.
Правильное сечение проводников, учет мощности оборудования и типа сети – важные факторы при организации электролинии. Диаметр кабеля можно несколькими способами вычислить самостоятельно. Основываясь на этих показаниях, легко определить сечение жил по формулам или с помощью таблицы.
Площадь треугольника, площадь прямоугольника, площадь трапеции, площадь квадрата, площадь круга, площадь полукруга и сектора, площадь параллелограмма. Площади плоских фигур. Формулы площади.
Площадь треугольника, площадь прямоугольника, площадь трапеции, площадь квадрата, площадь круга, площадь полукруга и сектора, площадь параллелограмма.
Справочно: число пи
Пример 1
Прямоугольный поднос имеет длину 900 мм и ширину 350 мм. Определить его площадь в а) мм2, б) в см2, в) в м2
Решение:
а) Площадь =длина*ширина=900*350=315000 мм2
б) 1 см2=100 мм2, следовательно,
315000 мм2=315000/100=3150 см2
1 м2=10000 см2, следовательно,
3150 см2=3150/10000=0.315 м2
Пример 2
Определить площадь поперечного сечения балки, изображенной на рисунке.
Сечение балки можно разделить на три отдельных прямоугольника, как показано на рисунке
Sa=3*50=150 мм2
Sb=(65-5-3)*4=228 мм2
Sc=60*5=300 мм2
Общая площадь балки 150+228+300=678 мм2=6.78 см2.
Пример 3
Определить площадь дорожки, показанной на рисунке.
Решение:
Площадь дорожки = площадь большого прямоугольника — площадь малого прямоугольника
S=35*15-29*11=206 м2
Пример 4
Определить площадь параллелограмма, показанного на рисунке (размеры приведены в миллиметрах).
Площадь параллелограмма = основание * высота. Высота h определяется по теореме Пифагора BC2=CE2+h2
Тогда
202=(36-30)2+h2
h2=202-62=164
h=14,3 (приблизительно)
Следовательно, Sabcd=30*14.3=429 мм2
Пример 5
Показана боковая сторона здания. Определить площадь кирпичной кладки на боковой стороне.
Боковая сторона состоит из прямоугольника и треугольника.
Sпрям.=6*10=60 м2
S треуг. =1/2*основание*высота
CD=5 м, AD=6 м, следовательно, AC=3 м (по т. Пифагора). Следовательно,
S треуг. =1/2*10*3=15 м2.
Общая площадь кирпичной кладки есть 60+15=75 м2
Пример 6
Определить площади кругов, имеющих а) радиус 3 см, б) диаметр 10 мм, в) длину окружности 60 мм.
S=πr2 или πd2/4.
а) S=πr2=π(3)2=9π=28.26 см2
б) S=πd2/4=π(10)2/4=100π/4=78.5 мм2
в) Длина окружности с=2πr, следовательно,
r=c/2π=60/2π=30/π
S=πr2=π(30/π)2=286.62 мм2
Пример 7
Вычислить площадь правильного восьмиугольника со стороной 5 см и поперечником 10 см.
Восьмиугольник — это многоугольник с 8 сторонами. Если из центра многоугольника провести лучи к вершинам, получится восемь одинаковых треугольников.
S треуг. =1/2*основание*высота=1/2*5*10/2=12.5 см2
Площадь восьмиугольника есть 8*12.5=100 см2
Пример 8
Определить площадь правильного шестиугольника со стороной 10 см.
Шестиугольник — это многоугольник с шестью сторонами, который может быть разбит на шесть равных треугольников, как показано на рис. сходящиеся в центре многоугольника углы треугольника равны 360о/6=60о
Другие два угла каждого треугольника составляют в сумме 120о и равны между собой.
Следовательно, все треугольники являются равносторонними с углами 60о и стороной 10 см
S треуг. =1/2*основание*высота
Высоту h находим по теореме Пифагора:
102=h2+52
Отсюда h2=100-25=75
h=8.66 см
Следовательно, S треуг. =1/2*10*8.66=43.3 см 2
Площадь шестиугольника равна 6*43.3=259.8 см2
особенности величины, как найти её для круга
В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).
Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Как рассчитать площадь поперечного сечения
Обновлено 7 февраля 2020 г.
Кевин Бек
Проверено: Lana Bandoim, B.S.
Вы можете столкнуться с ситуациями, в которых у вас есть трехмерное твердое тело и вам необходимо определить площадь воображаемой плоскости, вставленной через фигуру и имеющей границы, определяемые границами твердого тела.
Например, если под вашим домом проходит цилиндрическая труба длиной 20 метров (м) и 0.15 м в поперечнике, возможно, вы захотите узнать площадь поперечного сечения трубы.
Поперечные сечения могут быть перпендикулярны ориентации осей твердого тела, если таковые существуют. В случае сферы любая плоскость, пересекающая сферу, независимо от ориентации, приведет к получению диска определенного размера.
Площадь поперечного сечения зависит от формы твердого тела, определяющего границы поперечного сечения, и угла между осью симметрии твердого тела (если есть) и плоскостью, которая создает поперечное сечение.
Площадь поперечного сечения прямоугольного твердого тела
Объем любого прямоугольного твердого тела, включая куб, равен площади его основания (длина, умноженная на ширину), умноженной на его высоту: V = l × w × h.
Следовательно, если поперечное сечение параллельно верху или низу твердого тела, площадь поперечного сечения составляет l × w. Если плоскость сечения параллельна одной из двух сторон, площадь поперечного сечения задается как l × h или w × h.
Если поперечное сечение не перпендикулярно какой-либо оси симметрии, создаваемая форма может быть треугольником (если поместить его через угол твердого тела) или даже шестиугольником.
Пример: Вычислить площадь поперечного сечения плоскости, перпендикулярной основанию куба объемом 27 м. 3 .
Поскольку для куба l = w = h, длина любого ребра куба должна составлять 3 м (поскольку 3
× 3
× 3 = 27). Таким образом, поперечное сечение описанного типа представляет собой квадрат со стороной 3 м, что дает площадь 9 м 2 .
Площадь поперечного сечения цилиндра
Цилиндр — это твердое тело, образованное протяжением круга через пространство, перпендикулярное его диаметру.Площадь круга определяется формулой πr 2 , где r — радиус. Следовательно, имеет смысл, что объем цилиндра будет площадью одной из окружностей, образующих его основание.
Если поперечное сечение параллельно оси симметрии, то площадь поперечного сечения представляет собой просто окружность площадью πr 2 . Если секущая плоскость вставлена под другим углом, создается форма эллипса. Для определения площади используется соответствующая формула: πab (где a — наибольшее расстояние от центра эллипса до края, а b — самое короткое).
Пример: Какова площадь поперечного сечения трубы под вашим домом, описанной во введении?
Площадь поперечного сечения сферы
Любая теоретическая плоскость, проведенная через сферу, приведет к образованию круга (подумайте об этом на несколько минут). Если вам известен диаметр или длина окружности, образующей поперечное сечение, вы можете использовать соотношения C = 2πr и A = πr 2 для получения решения.
Пример : Плоскость грубо проходит через Землю очень близко к Северному полюсу, удаляя часть планеты в 10 м вокруг.Какова площадь поперечного сечения этого холодного кусочка Земли?
- Поскольку C = 2πr = 10 м, r = 10 / 2π = 1,59 м; A = πr 2 = π (1,59) 2 = 7,96 м 2 .
Расчет диаметра провода и площади поперечного сечения
В этом блоге мы рассмотрим концепцию сопротивления, удельного сопротивления и шаги для расчета минимальной площади поперечного сечения и диаметра любого желаемого проводника.
Что такое сопротивление?
Свойство устройства или цепи, препятствующее прохождению через нее тока.Сопротивление измеряется в Ом (Ом). Прочность любого материала с равномерной площадью поперечного сечения определяется следующими четырьмя факторами:
- Вид материала
- Длина
- Площадь поперечного сечения
- Температура
Что такое удельное сопротивление?
Удельное сопротивление — это мера того, насколько данный размер конкретного материала сопротивляется току. Хотя материалы сопротивляются прохождению электрического тока, некоторые из них проводят его лучше, чем другие.Удельное сопротивление используется для сравнения характеристик внутреннего сопротивления различных материалов. Материалы, которые легко проводят ток, называются проводниками. Проводники обладают низким удельным сопротивлением. В то время как материалы, которые с трудом проводят ток, называются изоляторами. Изоляторы обладают высоким сопротивлением. Удельное сопротивление материала играет важную роль при выборе материалов, используемых для электрического провода.
Теперь, когда мы ясно понимаем концепции сопротивления и удельного сопротивления, давайте рассмотрим общую взаимосвязь между основным сопротивлением проводника, которая предполагает, что сопротивление данного проводника равно удельному сопротивлению материала, умноженному на отношение его длины к площади его поперечного сечения. .Это может помочь нам рассчитать минимальную площадь поперечного сечения и диаметр любого желаемого проводника.
Давайте рассмотрим пример, чтобы понять, как вычислить минимальную площадь поперечного сечения и диаметр любого желаемого проводника.
Пример: Какова минимальная площадь поперечного сечения и диаметр жилы для медного провода длиной 750 метров с максимальным сопротивлением 0,2 Ом?
Минимальная площадь поперечного сечения:
Чтобы решить эту проблему, мы будем использовать общее соотношение для расчета сопротивления проводника по следующей формуле:
Сопротивление = Удельное сопротивление * (Длина / Площадь)
R =
R = Сопротивление материала, Ом
Ρ = Удельное сопротивление материала, Ом на метр
L = Длина проводника, в метрах
A = Площадь поперечного сечения, в квадратных метрах
Чтобы использовать это общее соотношение для решения нашей примерной проблемы, нам требуется удельное сопротивление или удельное сопротивление меди.Обратите внимание, что мы получаем удельное сопротивление материалов проводников из таблицы удельных сопротивлений проводников, и теперь мы знаем, что удельное сопротивление меди составляет 1,72 x 10e-8 Ом на метр.
При вычислении сопротивления проводника не забудьте выразить сопротивление в омах, удельное сопротивление материала в омах на метр, длину проводника в метрах и площадь поперечного сечения в квадратных метрах, чтобы это соотношение было действительным. Затем мы можем перейти к вычислению площади поперечного сечения провода, подставив известные величины в примере.
A = Ур. (1)
Диаметр жилы:
Площадь круга может быть представлена с помощью формулы ниже. Чтобы найти диаметр, нам придется изменить формулу.
А =
4 * А =
=
г =
Теперь мы можем заменить наше полученное значение площади поперечного сечения из уравнения. (1) в это соотношение и рассчитайте диаметр медной проволоки, чтобы получить диаметр 0.2 и диаметром не менее 9,062 мм.
Площадь поперечного сечения к диаметру пересечение круга пересечения диаметр поперечного сечения электрического кабеля формула проводника диаметр провода и расчетное сечение провода AGW American Wire Gauge Толстая площадь сплошного провода формула удельное сопротивление многожильный провод литц длина ток
Площадь поперечного сечения к диаметру преобразование круг пересечение поперечное сечение диаметр электрического кабеля формула проводника диаметр провода и сечение проводки и расчетное сечение AGW American Wire Gauge толстая площадь сплошного провода формула удельное сопротивление многожильный провод длина литца ток — sengpielaudio Sengpiel Berlin
Преобразование и расчет — сечение <> диаметр
● Диаметр кабеля по кругу площадь сечения и наоборот ●
электрический кабель , провод , провод , шнур ,
строка ,
проводка и веревка
| Поперечное сечение — это просто двухмерный вид среза через объект. Часто задаваемый вопрос: как преобразовать диаметр круглого провода d = 2 × r в площадь поперечного сечения круга или площадь поперечного сечения A (плоскость среза) в кабель диаметр d ? Почему значение диаметра больше, чем значение площади? Потому что это не то же самое. Сопротивление обратно пропорционально площади поперечного сечения провода. Требуемое поперечное сечение электрической линии зависит от следующих факторов: |
| Используемый браузер не поддерживает JavaScript. Вы увидите программу, но функция работать не будет. |
«Единицей» обычно являются миллиметры, но также могут быть дюймы, футы, ярды, метры (метры),
или сантиметры, если за площадь принять квадрат этой меры.
Литцовый провод (многожильный провод), состоящий из множества тонких проводов, требует на 14% большего диаметра по сравнению со сплошным проводом.
| Площадь поперечного сечения — это не диаметр. |
| Поперечное сечение — это площадь. Диаметр — это линейная мера. Это не может быть то же самое. Диаметр кабеля в миллиметрах |
| Поперечное сечение или площадь поперечного сечения — это площадь такого разреза. Это не обязательно должен быть круг. Имеющийся в продаже размер провода (кабеля) как площадь поперечного сечения: |
Расчет поперечного сечения A , ввод диаметра d = 2 r :
r = радиус провода или кабеля
d = 2 r = диаметр провод или кабель
Расчет диаметра d = 2 r , вход в сечение A :
Жила (электрокабель)
| На сопротивление проводника влияют четыре фактора: 1) площадь поперечного сечения проводника A , рассчитанная по диаметру d 2) длина проводника 3) температура в проводнике 4) материал, составляющий проводник |
| Нет точной формулы для минимального сечения провода из максимальной силы тока . Это зависит от многих обстоятельств, таких как, например, если расчет выполняется для постоянного, переменного тока или даже для трехфазного тока, свободно ли отпускается кабель или находится ли он под землей . Кроме того, это зависит от температуры окружающей среды, допустимой плотности тока и допустимого падения напряжения , а также от того, присутствует ли одножильный или многопроволочный провод. И всегда есть хороший, но неудовлетворительный совет использовать из соображений безопасности более толстый и, следовательно, более дорогой кабель .Часто задаваемые вопросы касаются падения напряжения на проводах. |
Падение напряжения Δ В
Формула падения напряжения с удельным сопротивлением (удельным сопротивлением) ρ (rho):
I = ток в амперах |
|
Производная единица удельного электрического сопротивления в системе СИ ρ — Ом × м, сокращенная от
прозрачный Ω × мм / м.
Электропроводность равна удельному электрическому сопротивлению.
Электропроводность и удельное электрическое сопротивление κ или σ = 1/ ρ
Электропроводность и электрическое сопротивление ρ = 1/ κ = 1/
Разница между удельным электрическим сопротивлением и электропроводностью
| Проводимость в сименсах обратно пропорциональна сопротивлению в омах. |
| Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обоих направлениях знака ↔ . |
| Величина электропроводности (проводимости) и удельного электрического сопротивления (удельное сопротивление) зависит от температуры материала постоянной. Чаще всего его дают при 20 или 25 ° C. |
Сопротивление = удельное сопротивление x длина / площадь
| Удельное сопротивление проводников изменяется с температурой. В ограниченном диапазоне температур он примерно линейен: , где α — температурный коэффициент, T — температура и T 0 — любая температура, |
Преобразование сопротивления в электрическую проводимость
Преобразование обратного сименса в ом
1 Ом [Ом] = 1 / сименс [1 / S]
1 сименс [S] = 1 / Ом [1 / Ом]
| Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обоих направлениях знака ↔ . |
1 миллисименс = 0,001 МОНО = 1000 Ом
| Математически проводимость обратно пропорциональна сопротивлению: Символом проводимости является заглавная буква «G», а единицей измерения является |
Калькулятор: закон Ома
Таблица типовых кабелей для громкоговорителей
| Диаметр кабеля d | 0.798 мм | 0,977 мм | 1,128 мм | 1,382 мм | 1.784 мм | 2,257 мм | 2.764 мм | 3,568 мм |
| Номинальное сечение кабеля A | 0,5 мм 2 | 0,75 мм 2 | 1,0 мм 2 | 1,5 мм 2 | 2,5 мм 2 | 4,0 мм 2 | 6,0 мм 2 | 10.0 мм 2 |
| Максимальный электрический ток | 3 А | 7,6 А | 10,4 А | 13,5 А | 18,3 А | 25 А | 32 А | – |
Всегда учитывайте, что поперечное сечение должно быть больше при большей мощности и большей длине
кабеля, но также и с меньшим сопротивлением. Вот таблица, в которой указаны возможные потери мощности.
| Длина кабеля в м | Сечение в мм 2 | Сопротивление Ом | Потери мощности при | Коэффициент демпфирования при | ||
| Импеданс 8 Ом | Импеданс 4 Ом | Импеданс 8 Ом | Импеданс 4 Ом | |||
| 1 | 0.75 | 0,042 | 0,53% | 1,05% | 98 | 49 |
| 1,50 | 0,021 | 0,31% | 0,63% | 123 | 62 | |
| 2,50 | 0,013 | 0,16% | 0,33% | 151 | 75 | |
| 4,00 | 0,008 | 0,10% | 0,20% | 167 | 83 | |
| 2 | 0.75 | 0,084 | 1,06% | 2,10% | 65 | 33 |
| 1,50 | 0,042 | 0,62% | 1,26% | 85 | 43 | |
| 2,50 | 0,026 | 0,32% | 0,66% | 113 | 56 | |
| 4,00 | 0,016 | 0,20% | 0,40% | 133 | 66 | |
| 5 | 0.75 | 0,210 | 2,63% | 5,25% | 32 | 16 |
| 1,50 | 0,125 | 1,56% | 3,13% | 48 | 24 | |
| 2,50 | 0,065 | 0,81% | 1,63% | 76 | 38 | |
| 4,00 | 0,040 | 0,50% | 1,00% | 100 | 50 | |
| 10 | 0.75 | 0,420 | 5,25% | 10,50% | 17 | 9 |
| 1,50 | 0,250 | 3,13% | 6,25% | 28 | 14 | |
| 2,50 | 0,130 | 1,63% | 3,25% | 47 | 24 | |
| 4,00 | 0,080 | 1,00% | 2,00% | 67 | 33 | |
| 20 | 0.75 | 0,840 | 10,50% | 21,00% | 9 | 5 |
| 1,50 | 0,500 | 6,25% | 12,50% | 15 | 7 | |
| 2,50 | 0,260 | 3,25% | 6,50% | 27 | 13 | |
| 4,00 | 0,160 | 2,00% | 4,00% | 40 | 20 | |
Значения коэффициента демпфирования показывают, что осталось от принятого коэффициента демпфирования 200
в зависимости от длины кабеля, поперечного сечения и импеданса громкоговорителя.
Преобразование и расчет диаметра кабеля в AWG
и AWG в диаметр кабеля в мм — American Wire Gauge
| Чаще всего мы используем четные числа, например 18, 16, 14 и т. Д. Если вы получили нечетный ответ, например 17, 19 и т. Д., Используйте следующее меньшее четное число. AWG обозначает американский калибр проводов и указывает на прочность проводов. |
Американский калибр проволоки — Таблица AWG
| AWG номер | 46 | 45 | 44 | 43 | 42 | 41 | 40 | 39 | 38 | 37 | 36 | 35 | 34 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Диаметр дюйм | 0.0016 | 0,0018 | 0,0020 | 0,0022 | 0,0024 | 0,0027 | 0,0031 | 0,0035 | 0,0040 | 0,0045 | 0,0050 | 0,0056 | 0,0063 |
| Диаметр (Ø) в мм | 0,04 | 0,05 | 0,05 | 0,06 | 0,06 | 0,07 | 0,08 | 0,09 | 0,10 | 0,11 | 0.13 | 0,14 | 0,16 |
| Поперечное сечение в мм 2 | 0,0013 | 0,0016 | 0,0020 | 0,0025 | 0,0029 | 0,0037 | 0,0049 | 0,0062 | 0,0081 | 0,010 | 0,013 | 0,016 | 0,020 |
| AWG номер | 33 | 32 | 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 |
| Диаметр дюйм | 0.0071 | 0,0079 | 0,0089 | 0,0100 | 0,0113 | 0,0126 | 0,0142 | 0,0159 | 0,0179 | 0,0201 | 0,0226 | 0,0253 | 0,0285 |
| Диаметр (Ø) в мм | 0,18 | 0,20 | 0,23 | 0,25 | 0,29 | 0,32 | 0,36 | 0,40 | 0,45 | 0,51 | 0.57 | 0,64 | 0,72 |
| Поперечное сечение в мм 2 | 0,026 | 0,032 | 0,040 | 0,051 | 0,065 | 0,080 | 0,10 | 0,13 | 0,16 | 0,20 | 0,26 | 0,32 | 0,41 |
| AWG номер | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 |
| Диаметр дюйм | 0.0319 | 0,0359 | 0,0403 | 0,0453 | 0,0508 | 0,0571 | 0,0641 | 0,0719 | 0,0808 | 0,0907 | 0,1019 | 0,1144 | 0,1285 |
| Диаметр (Ø) в мм | 0,81 | 0,91 | 1,02 | 1,15 | 1,29 | 1,45 | 1,63 | 1,83 | 2,05 | 2,30 | 2.59 | 2,91 | 3,26 |
| Поперечное сечение в мм 2 | 0,52 | 0,65 | 0,82 | 1,0 | 1,3 | 1,7 | 2,1 | 2,6 | 3,3 | 4,2 | 5,3 | 6,6 | 8,4 |
| AWG номер | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 (1/0) (0) | 00 (2/0) (-1) | 000 (3/0) (-2) | 0000 (4/0) (-3) | 00000 (5/0) (-4) | 000000 (6/0) (-5) |
| Диаметр дюйм | 0.1443 | 0,1620 | 0,1819 | 0,2043 | 0,2294 | 0,2576 | 0,2893 | 0,3249 | 0,3648 | 0,4096 | 0,4600 | 0,5165 | 0,5800 |
| Диаметр (Ø) в мм | 3,67 | 4,11 | 4,62 | 5,19 | 5,83 | 6,54 | 7,35 | 8,25 | 9,27 | 10,40 | 11.68 | 13,13 | 14,73 |
| Поперечное сечение в мм 2 | 10,6 | 13,3 | 16,8 | 21,1 | 26,7 | 33,6 | 42,4 | 53,5 | 67,4 | 85,0 | 107,2 | 135,2 | 170,5 |
Как высокие частоты демпфируются длиной кабеля?
Обучение расчету сечения
С технической точки зрения, поперечное сечение — это когда плоскость встречается с твердой формой.Вычисление очень похоже на вычисление площади фигуры; единственная разница в том, что поперечное сечение является частью трехмерной формы. Различные формы имеют разные формулы, и ниже приведены некоторые примеры того, как проводить вычисления.
Прямоугольники
Вы можете увидеть прямоугольное поперечное сечение прямоугольного здания, коробки с хлопьями или чего-то еще, что представляет собой прямоугольную призму. Это может быть проще всего вычислить площадь поперечного сечения, так как это просто ширина x длина.Например, предположим, что одна сторона здания восьми футов в длину, а другая — шести футов в длину. Восемь, умноженная на шесть, дает 48, и вот вам поперечное сечение.
Квадраты
Вы можете увидеть квадратное поперечное сечение в кости или в пирамиде с квадратным основанием, как в Египте. Поскольку все стороны квадрата имеют одинаковую длину, поперечное сечение — это просто длина, умноженная на себя. Например, если длина кости составляет два дюйма, площадь поперечного сечения составляет четыре дюйма в квадрате.Легкий способ запомнить это: поперечное сечение квадрата — это квадрат длины.
Треугольники
Треугольное поперечное сечение может быть не таким распространенным, как другие формы, поскольку вы, вероятно, видели бы его только в пирамиде с треугольным основанием или треугольной призме. Самый простой способ найти эту площадь поперечного сечения — это умножить базовую длину на высоту и затем разделить на два. Однако эти длины может быть сложно найти, если они не указаны, и вам нужно будет полагаться на тригонометрию, чтобы найти любые недостающие цифры.
Круги
Площадь поперечного сечения круга довольно сложна, так как обычно требуется калькулятор для получения точного числа, поскольку оно включает число Пи. Формы с круглым поперечным сечением включают конусы, сферы и цилиндры. Площадь круга равна двум x пи x квадрату радиуса. Радиус равен половине диаметра, который равен длине реза по окружности. Если вам не нужно точное число, вы можете просто оставить результат с пи. Например, если радиус составляет пять дюймов, площадь поперечного сечения будет равна двум x пи x 25, что в конечном итоге будет равно 50 x pi без калькулятора.
Дополнительные шаги
Хотя основное внимание здесь уделяется площади поперечного сечения формы, вы можете легко найти объем формы с помощью этой информации. Для большинства форм вы просто умножаете площадь поперечного сечения на длину объекта. Определенные формы, такие как сферы и конусы, имеют разные формулы, а это означает, что это не универсальное правило.
Это всего лишь простое руководство по расчету основных площадей поперечного сечения. Большинство форм можно разбить на эти четыре более простые формы.Самая сложная часть поперечных сечений — это возможность визуализировать, как выглядит форма, когда она разрезана. Зная форму поперечного сечения, вы можете легко применить одну из этих формул и провести математические вычисления.
жидкостей в движении | Безграничная физика
Расход и уравнение непрерывности
Расход жидкости — это то, сколько жидкости проходит через область за заданное время.
Цели обучения
Определение расхода на основе скорости и площади или прошедшего времени и обоснование использования непрерывности при выражении свойств жидкости и ее движения
Основные выводы
Ключевые моменты
- Расход можно выразить либо через площадь поперечного сечения и скорость, либо через объем и время.
- Поскольку жидкости несжимаемы, скорость потока в область должна равняться скорости потока из области. Это известно как уравнение неразрывности.
- Уравнение неразрывности может показать, насколько увеличивается скорость жидкости, если она вынуждена течь через меньшую площадь. Например, если площадь трубы уменьшится вдвое, скорость жидкости увеличится вдвое.
- Хотя газы часто ведут себя как жидкости, они не несжимаемы, как жидкости, и поэтому уравнение неразрывности не применяется.
Ключевые термины
- несжимаемый : Невозможно сжимать или конденсировать.
- непрерывность : Отсутствие прерывания или отключения; качество непрерывности в пространстве или времени.
Расход жидкости — это объем жидкости, который проходит через поверхность в заданную единицу времени. Обычно обозначается символом Q.
.
Уравнение непрерывности для жидкостей : Краткое введение в уравнение непрерывности для жидкостей.
Расход
Объемный расход определяется как
[латекс] \ text {Q} = \ text {v} * \ text {a} [/ latex],
, где Q — скорость потока, v — скорость жидкости, а a — площадь поперечного сечения пространства, через которое движется жидкость. Объемный расход также можно найти с помощью
.
[латекс] \ text {Q} = \ frac {\ text {V}} {\ text {t}} [/ latex]
где Q — расход, V — объем жидкости, а t — прошедшее время.
Непрерывность
Уравнение неразрывности работает в предположении, что входящий поток равен выходному.Это может быть полезно для решения многих свойств жидкости и ее движения:
Входящий поток = Выходящий : Используя известные свойства жидкости при одном условии, мы можем использовать уравнение неразрывности для определения свойств той же жидкости при других условиях.
[латекс] \ text {Q} _1 = \ text {Q} _2 [/ латекс]
Это может быть выражено разными способами, например: [латекс] \ text {A} _1 * \ text {v} _1 = \ text {A} _2 * \ text {v} _2 [/ latex]. Уравнение неразрывности применимо к любой несжимаемой жидкости.Поскольку жидкость не может сжиматься, количество жидкости, которая втекает на поверхность, должно равняться количеству, вытекающему с поверхности.
Применение уравнения непрерывности
Вы можете наблюдать действие уравнения неразрывности в садовом шланге. Вода течет по шлангу, и когда она достигает более узкого сопла, скорость воды увеличивается. Скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда увеличивается площадь поперечного сечения. Это следствие уравнения неразрывности.Если поток Q остается постоянным, когда площадь A уменьшается, скорость v должна увеличиваться пропорционально. Например, если сопло шланга составляет половину площади шланга, скорость должна удвоиться, чтобы поддерживать непрерывный поток.
Размер проводника
| Физика проводников и изоляторов
Это должно быть здравым смыслом, что жидкость течет по трубам большого диаметра легче, чем по трубам малого диаметра (если вам нужна практическая иллюстрация, попробуйте пить жидкость через соломинку разного диаметра).Тот же общий принцип действует для потока электронов через проводники: чем шире площадь поперечного сечения (толщина) проводника, тем больше места для протекания электронов и, следовательно, тем легче возникает поток (меньшее сопротивление). .
Два основных вида электрического провода: одножильный и многожильный
Электрический провод обычно имеет круглое сечение (хотя есть некоторые уникальные исключения из этого правила) и бывает двух основных разновидностей: , , одножильный, и многожильный, , . Сплошной медный провод — это так, как звучит: одна сплошная медная жила по всей длине провода. Многожильный провод состоит из более мелких жил сплошного медного провода, скрученных вместе в один провод большего размера. Самым большим преимуществом многожильного провода является его механическая гибкость, способность выдерживать многократные изгибы и скручивания намного лучше, чем сплошная медь (которая со временем склонна к усталости и ломается).
Размер провода можно измерить несколькими способами.Мы могли бы говорить о диаметре провода, но поскольку на самом деле площадь поперечного сечения имеет наибольшее значение для потока электронов, нам лучше определять размер провода в терминах площади.
Изображение сечения провода, показанное выше, конечно, не в масштабе. Диаметр показан как 0,1019 дюйма. Вычисляя площадь поперечного сечения по формуле Area = πr 2 , получаем площадь 0,008155 квадратных дюймов:
Это довольно маленькие числа для работы, поэтому размеры проводов часто выражаются в единицах измерения тысячных долей дюйма, или мил .Для проиллюстрированного примера мы бы сказали, что диаметр проволоки составляет 101,9 мил (0,1019 дюйма на 1000). Мы также могли бы, если бы захотели, выразить площадь провода в квадратных милях, вычислив это значение с помощью той же формулы площади круга: Площадь = πr 2 :
Расчет круговой миловой площади провода
Однако электрики и другие лица, часто озабоченные размером провода, используют другую единицу измерения площади, специально разработанную для круглого сечения провода.Эта специальная единица называется круговых мил (иногда сокращенно см ). Единственная цель наличия этой специальной единицы измерения состоит в том, чтобы исключить необходимость использования коэффициента π (3,1415927 …) в формуле для вычисления площади, а также необходимости вычислить радиус провода , когда вам дали диаметр . . Формула для расчета площади в миле круглого провода очень проста:
Поскольку это единица измерения площади , математическая степень 2 все еще действует (удвоение ширины круга всегда увеличивает его площадь в четыре раза, независимо от того, какие единицы используются, или если ширина этого круга выражается в единицах радиуса или диаметра).Чтобы проиллюстрировать разницу между измерениями в квадратных милях и измерениями в круглых милах, я сравню круг с квадратом, показывая площадь каждой формы в обеих единицах измерения:
А для провода другого размера:
Очевидно, круг данного диаметра имеет меньшую площадь поперечного сечения, чем квадрат ширины и высоты, равный диаметру круга: обе единицы измерения площади отражают это. Однако должно быть ясно, что единица «квадратный мил» действительно предназначена для удобного определения площади квадрата, в то время как «круговой мил» адаптирован для удобного определения площади круга: соответствующую формулу для каждого проще работать с.Следует понимать, что обе единицы действительны для измерения площади формы, независимо от того, какой формы она может быть. Преобразование между круглыми милами и квадратными милами представляет собой простое соотношение: на каждые 4 круглых мила приходится π (3,1415927 …) квадратных милов.
Измерение площади поперечного сечения провода с помощью калибра
Еще одним средством измерения площади поперечного сечения провода является калибр . Шкала датчика основана на целых числах, а не на дробных или десятичных дюймах. Чем больше номер калибра, тем тоньше провод; чем меньше номер калибра, тем толще проволока.Для тех, кто знаком с ружьем, эта обратно пропорциональная шкала измерения должна показаться знакомой.
Таблица в конце этого раздела приравнивает калибр к диаметру в дюймах, круглые милы и квадратные дюймы для сплошной проволоки. Провода большего диаметра достигают конца общей шкалы калибра (которая, естественно, достигает максимума, равного 1), и представлены серией нулей. «3/0» — это еще один способ представления «000», который произносится как «тройной дол». Опять же, тем, кто знаком с ружьями, следует признать терминологию, как бы странно это ни звучало.Что еще больше усложняет ситуацию, в мире существует более одного «стандарта» калибра. Для определения размеров электрических проводов предпочтительной измерительной системой является калибр American Wire Gauge (AWG), также известный как калибр Brown и Sharpe (B&S). В Канаде и Великобритании Британский стандартный калибр проводов (SWG) является официальной системой измерения электрических проводов. В мире существуют другие системы калибровки проволоки для классификации диаметра проволоки, такие как Stubs калибр для стальной проволоки и Steel Music Wire Gauge (MWG), но эти системы измерения применимы к неэлектрическим проводам.
Система измерения American Wire Gauge (AWG), несмотря на ее странности, была разработана с целью: на каждые три шага на шкале калибра площадь провода (и вес на единицу длины) примерно удваивается. Это удобное правило, которое следует помнить при приблизительной оценке диаметра проволоки!
Для очень проводов большого диаметра (толще 4/0) от системы калибров обычно отказываются для измерения площади поперечного сечения в тысячах круглых мил (MCM), заимствуя старую римскую цифру «M» для обозначения кратного от «тысячи» перед «CM» для «круговых мил.В следующей таблице размеров проводов не указаны размеры, превышающие калибр 4/0, потому что сплошной медный провод становится непрактичным для обращения с такими размерами. Вместо этого предпочтение отдается многопроволочной конструкции.
Таблица проводов для сплошных круглых медных проводников
| Размер | Диаметр | Площадь поперечного сечения | Вес | |
|---|---|---|---|---|
| AWG | дюймов | cir. мил | кв. Дюймов | фунтов / 1000 футов |
| 4/0 | 0.4600 | 211 600 | 0,1662 | 640,5 |
| 3/0 | 0,4096 | 167 800 | 0,1318 | 507,9 |
| 2/0 | 0,3648 | 133,100 | 0,1045 | 402,8 |
| 1/0 | 0,3249 | 105 500 | 0,08289 | 319,5 |
| 1 | 0,2893 | 83 690 | 0.06573 | 253,5 |
| 2 | 0,2576 | 66,370 | 0,05213 | 200,9 |
| 3 | 0,2294 | 52 630 | 0,04134 | 159,3 |
| 4 | 0,2043 | 41740 | 0,03278 | 126,4 |
| 5 | 0,1819 | 33,100 | 0,02600 | 100,2 |
| 6 | 0.1620 | 26 250 | 0,02062 | 79,46 |
| 7 | 0,1443 | 20 820 | 0,01635 | 63,02 |
| 8 | 0,1285 | 16 510 | 0,01297 | 49,97 |
| 9 | 0,1144 | 13 090 | 0,01028 | 39,63 |
| 10 | 0,1019 | 10,380 | 0,008155 | 31.43 |
| 11 | 0,09074 | 8 234 | 0,006467 | 24,92 |
| 12 | 0,08081 | 6 530 | 0,005129 | 19,77 |
| 13 | 0,07196 | 5 178 | 0,004067 | 15,68 |
| 14 | 0,06408 | 4,107 | 0,003225 | 12,43 |
| 15 | 0.05707 | 3 257 90 253 | 0,002558 | 9,858 |
| 16 | 0,05082 | 2,583 | 0,002028 | 7,818 |
| 17 | 0,04526 | 2,048 | 0,001609 | 6.200 |
| 18 | 0,04030 | 1,624 | 0,001276 | 4,917 |
| 19 | 0,03589 | 1,288 | 0.001012 | 3,899 |
| 20 | 0,03196 | 1 022 90 253 | 0,0008023 | 3,092 |
| 21 | 0,02846 | 810,1 | 0,0006363 | 2.452 |
| 22 | 0,02535 | 642,5 | 0,0005046 | 1,945 |
| 23 | 0,02257 | 509,5 | 0,0004001 | 1,542 |
| 24 | 0.02010 | 404,0 | 0,0003173 | 1,233 |
| 25 | 0,01790 | 320,4 | 0,0002517 | 0,9699 |
| 26 | 0,01594 | 254,1 | 0,0001996 | 0,7692 |
| 27 | 0,01420 | 201,5 | 0,0001583 | 0,6100 |
| 28 | 0,01264 | 159,8 | 0.0001255 | 0,4837 |
| 29 | 0,01126 | 126,7 | 0,00009954 | 0,3836 |
| 30 | 0,01003 | 100,5 | 0,00007894 | 0,3042 |
| 31 | 0,008928 | 79,70 | 0,00006260 | 0,2413 |
| 32 | 0,007950 | 63,21 | 0,00004964 | 0.1913 |
| 33 | 0,007080 | 50,13 | 0,00003937 | 0,1517 |
| 34 | 0,006305 | 39,75 | 0,00003122 | 0,1203 |
| 35 | 0,005615 | 31,52 | 0,00002476 | 0,09542 |
| 36 | 0,005000 | 25,00 | 0,00001963 | 0,07567 |
| 37 | 0.004453 | 19,83 | 0,00001557 | 0,06001 |
| 38 | 0,003965 | 15,72 | 0,00001235 | 0,04759 |
| 39 | 0,003531 | 12,47 | 0,000009793 | 0,03774 |
| 40 | 0,003145 | 9,888 | 0,000007766 | 0,02993 |
| 41 | 0,002800 | 7.842 | 0,000006159 | 0,02374 |
| 42 | 0,002494 | 6,219 | 0,000004884 | 0,01882 |
| 43 | 0,002221 | 4,932 | 0,000003873 | 0,01493 |
Для некоторых сильноточных приложений требуются провода сечением, превышающим практический предел размера круглого провода. В этих случаях в качестве проводников используются толстые шины из цельного металла, называемые сборными шинами .Шины обычно изготавливаются из меди или алюминия и чаще всего неизолированы. Они физически поддерживаются вдали от каркаса или конструкции, удерживающей их, с помощью опорных изоляторов. Хотя квадратное или прямоугольное поперечное сечение очень распространено для формы шин, используются также и другие формы. Площадь поперечного сечения шин обычно измеряется в круглых милах (даже для квадратных и прямоугольных шин!), Скорее всего, для удобства возможности напрямую приравнять размер шины к круглому проводу.
ОБЗОР:
- Ток протекает по проводам большого диаметра легче, чем по проводам малого диаметра, из-за большей площади поперечного сечения, по которой они могут двигаться.
- Вместо того, чтобы измерять небольшие размеры проволоки в дюймах, часто используется единица измерения «мил» (1/1000 дюйма).
- Площадь поперечного сечения провода может быть выражена в квадратных единицах (квадратные дюймы или квадратные милы), круговые милы или «калибровочная» шкала.
- При вычислении площади квадратной единицы для круглого провода используется формула площади круга:
- A = πr 2 (квадратные единицы)
- Расчет площади круглой проволоки в миле для круглой проволоки намного проще из-за того, что единица измерения «круговой мил» была выбрана именно для этой цели: чтобы исключить факторы «пи» и d / 2 (радиус) в формула.
- A = d 2 (круглые)
- На каждые 4 круговых мил приходится π (3,1416) квадратных милов.
- Система калибровки проводов калибра основана на целых числах, большие числа представляют провода меньшего сечения и наоборот. Провода толще 1 калибра обозначаются нулями: 0, 00, 000 и 0000 (произносятся «одинарная», «двойная», «тройная» и «четверная».
- Очень большие сечения проводов измеряются в тысячах круглых милов (MCM), что типично для шин и проводов сечением выше 4/0.
- Шины — это сплошные шины из меди или алюминия, используемые в конструкции сильноточных цепей. Соединения, выполняемые с шинами, обычно являются сварными или болтовыми, а шины часто голые (неизолированные) и поддерживаются вдали от металлических каркасов за счет использования изолирующих стоек.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ :
Объем твердого тела с известным поперечным сечением
В этом разделе мы узнаем, как найти объем твердого объекта, имеющего известные поперечные сечения.
Мы рассматриваем твердые тела, поперечные сечения которых имеют обычную форму, такую как треугольники, квадраты, прямоугольники, трапеции и полукруги. 2}}}} \ normalsize \) и плоскость \ (z = 1.2} = 1, \) и каждое перпендикулярное поперечное сечение представляет собой квадрат.
Пример 6
Найдите объем усеченного конуса, если его основания представляют собой эллипсы с полуосями \ (A, B, \) и \ (a, b \), а альтитур равен \ (H. \)
Пример 7
Вычислите объем клина с учетом нижних сторон \ (a, b, \), верхней стороны \ (c, \) и высоты \ (H. \).
Пример 8
Найдите объем правильного тетраэдра с ребром \ (a. \)
Пример 9
Клин вырезается из кругового цилиндра радиуса \ (R \) и высоты \ (H \) плоскостью, проходящей через диаметр основания (рисунок \ (10 \)).Найдите объем цилиндрического клина.
Пример 10
Оси двух круговых цилиндров одинакового радиуса \ (R \) пересекаются под прямым углом. Найдите объем твердого тела, общего для обоих этих цилиндров.
Пример 1.
Твердое тело имеет основание, лежащее в первом квадранте плоскости \ (xy — \) и ограниченное прямыми \ (y = x, \) \ (x = 1, \) \ (y = 0. 2}}}.H {A \ left (x \ right) dx}, \]
, где \ ({A \ left (x \ right)} \) — площадь поперечного сечения в точке \ (x. \)
Длины большой и малой осей линейно изменяются от \ (a, b \) до \ (A, B, \) и в точке \ (x \) определяются следующими выражениями:
\ [{\ text {большая ось:} \; \; a + \ left ({A — a} \ right) \ frac {x} {H} \; \;} \ kern0pt {\ text {малая ось: } \; \; b + \ left ({B — b} \ right) \ frac {x} {H}}. \]
Теперь посчитаем площадь поперечного сечения:
\ [{A \ left (x \ right) \ text {=}} \ kern0pt {\ pi \ left ({a + \ left ({A — a} \ right) \ frac {x} {H}} \ справа) \ left ({b + \ left ({B — b} \ right) \ frac {x} {H}} \ right)} = {\ pi \ left [{ab + b \ left ({A — a } \ right) \ frac {x} {H}} \ right.H {A \ left (x \ right) dx}} = {\ pi \ left [{abH + \ left ({bA + ab — 2ab} \ right) \ frac {H} {2}} \ right.} + {\ left. {\ left ({AB — aB — bA + ab} \ right) \ frac {H} {3}} \ right]} = {\ pi \ left [{\ cancel {abH} + \ frac { {bAH}} {2}} \ right.} + {\ left. {\ frac {{aBH}} {2} — \ cancel {abH}} \ right.} + {\ left. {\ frac {{ABH }} {3} — \ frac {{aBH}} {3}} \ right.} — {\ left. {\ Frac {{bAH}} {3} + \ frac {{abH}} {3}} \ right]} = {\ pi \ left [{\ frac {{bAH}} {6} + \ frac {{aBH}} {6}} \ right.} + {\ left. {\ frac {{ABH}}} {3} + \ frac {{abH}} {3}} \ right]} = {\ frac {{\ pi H}} {6} \ left [{bA + aB + 2AB + 2ab} \ right]} = {\ frac {{\ pi H}} {6} \ left [{\ left ({2A + a} \ right) B + \ left ({A + 2a} \ right) b} \ right].} \]
Пример 7.
Вычислите объем клина с учетом нижних сторон \ (a, b, \), верхней стороны \ (c, \) и высоты \ (H. \).
Решение.
Рис. 8.
Рассмотрим произвольное поперечное сечение на высоте \ (x. \). Это поперечное сечение представляет собой прямоугольник со сторонами \ (m \) и \ (n. \). Легко видеть, что
\ [{m = c + \ left ({a — c} \ right) \ frac {x} {h}, \; \;} \ kern0pt {n = \ frac {{bx}} {h}.} \]
Тогда площадь поперечного сечения \ (A \ left (x \ right) \) записывается как
\ [{A \ left (x \ right) = mn} = {\ left ({c + \ left ({a — c} \ right) \ frac {x} {h}} \ right) \ frac {{ bx}} {h}} = {\ frac {{bcx}} {h} + \ frac {{ab {x ^ 2}}} {{{h ^ 2}}} — \ frac {{bc {x ^ 2}}} {{{h ^ 2}}}} = {\ frac {{bcx}} {h} + \ frac {{b \ left ({a — c} \ right) {x ^ 2}}} {{{h ^ 2}}}.2} H}} = \ frac {2} {{3 \ pi}} \ приблизительно 0,212 \]
от общего объема цилиндра. Результат не зависит от \ (R \) и \ (H! \)
Пример 10.
Оси двух круговых цилиндров одинакового радиуса \ (R \) пересекаются под прямым углом. Найдите объем твердого тела, общего для обоих этих цилиндров.
Решение.
На рисунке ниже показано \ (\ large {\ frac {1} {8}} \ normalsize \) тела пересечения.
Рис. 11.
Рассмотрим поперечное сечение \ (ABCD \), перпендикулярное оси \ (x — \) в произвольной точке \ (x \).3}}} {3}} \]
.
 Такие приборы называют планиметрами.
Такие приборы называют планиметрами.
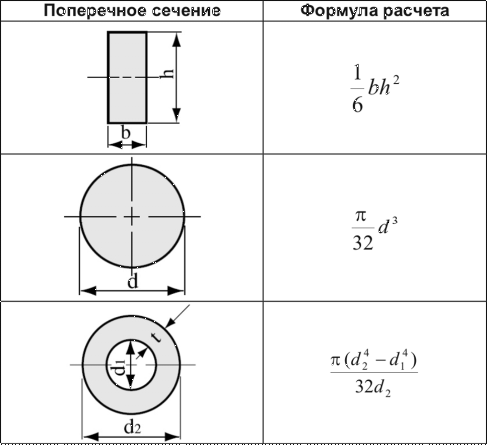
 Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C;
Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C; Температурный эксплуатационный режим составляет от минус 40 °C до плюс 80 °C.
Температурный эксплуатационный режим составляет от минус 40 °C до плюс 80 °C. Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C;
Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C; Температурный эксплуатационный режим составляет от минус 40 °C до плюс 80 °C.
Температурный эксплуатационный режим составляет от минус 40 °C до плюс 80 °C.