Как посчитать площадь комнаты, стены, пола, потолка
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.
Часто требуется посчитать кубатуру комнаты, ее объем
Содержание статьи
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Как высчитать площадь комнаты
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Площадь комнаты сложной формы
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
- Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже).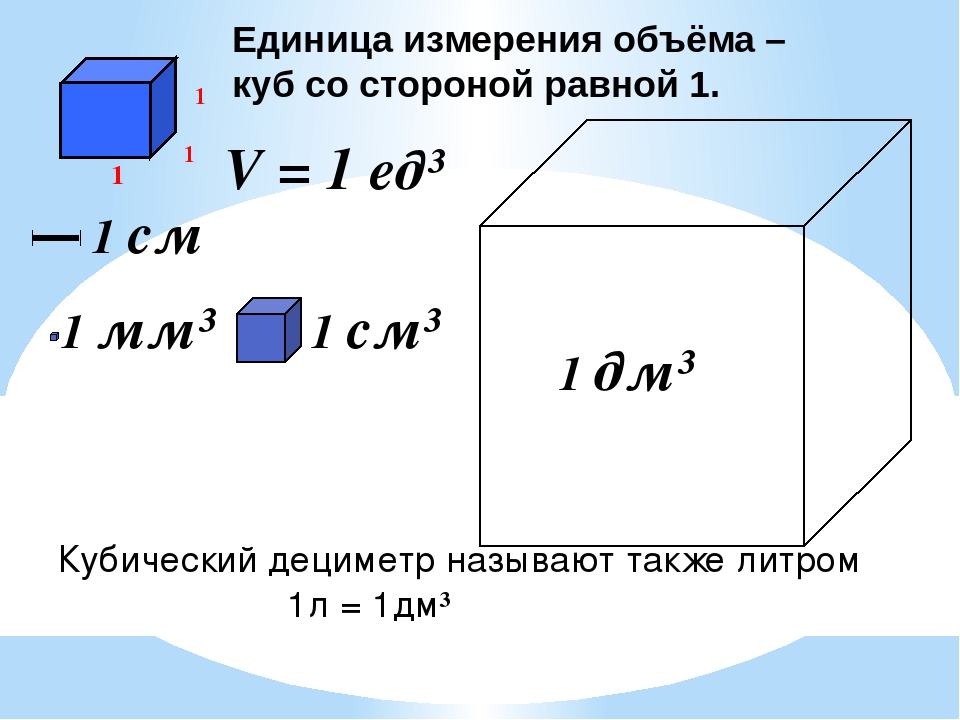 Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
Как посчитать площадь комнаты неправильной формы
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
- Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Формулы расчета площади и периметра простых геометрических фигур
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.
Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
Удобнее всего размеры наносить на план
Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем.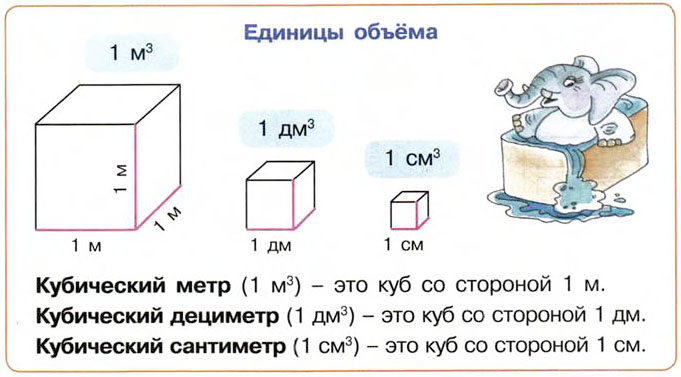 Для примера рассчитаем площадь стен, изображенных на схеме выше.
Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты
Формула расчета объема комнаты
Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.

Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м3. Итак, объем помещения 44,8 куба.
Периметр, площадь и объем
Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей).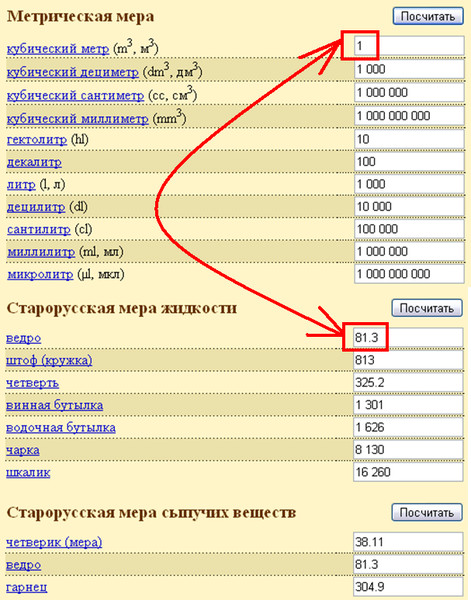 Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:
Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру.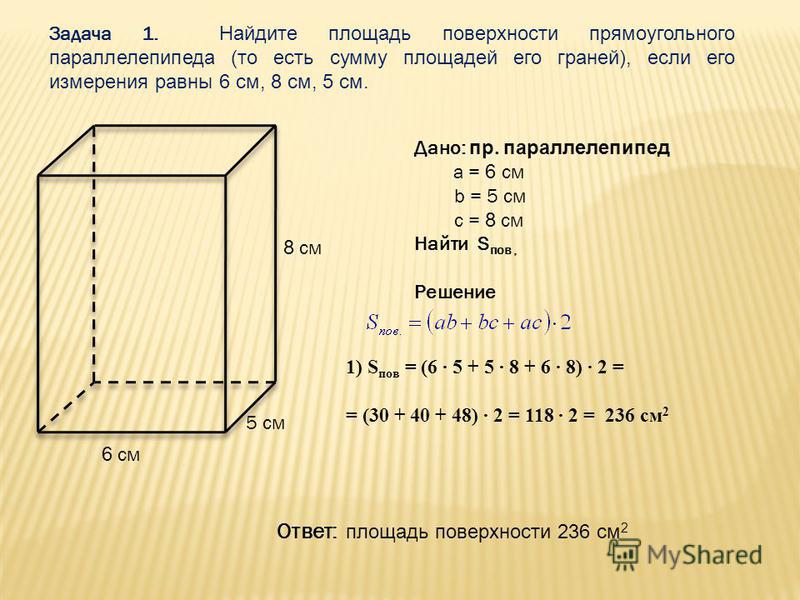 Площадь составила 12 квадратных метров.
Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
Тогда все четыре стороны тоже имеют длину, равную 100 см
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.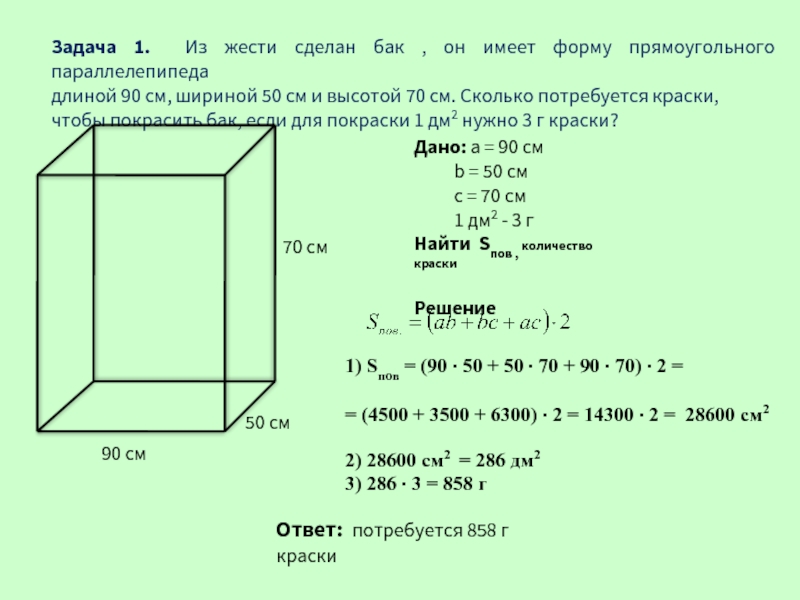
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .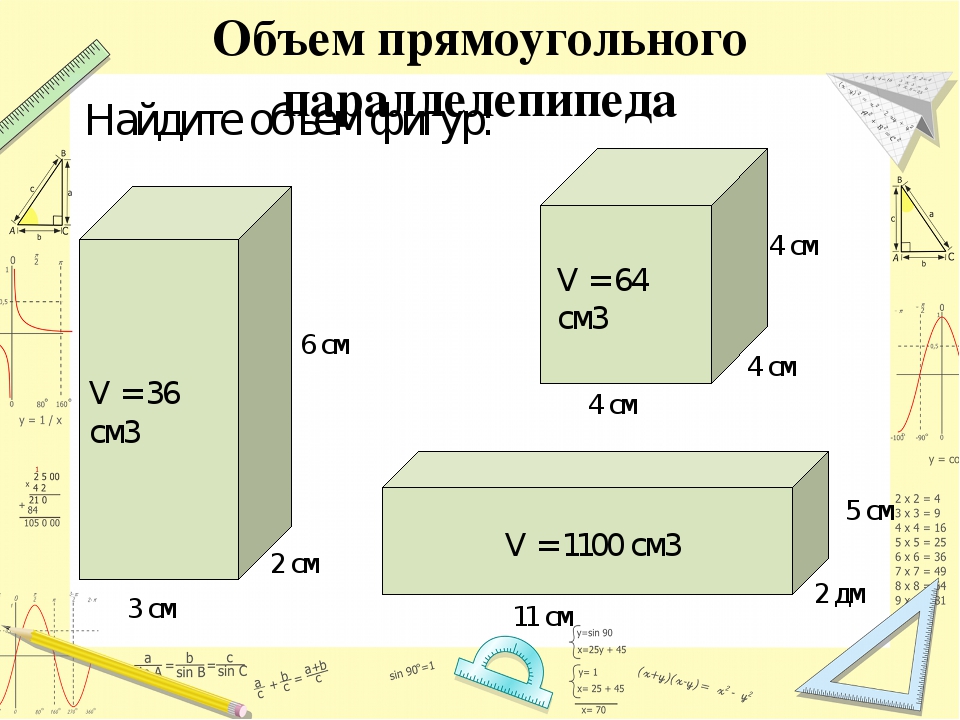
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).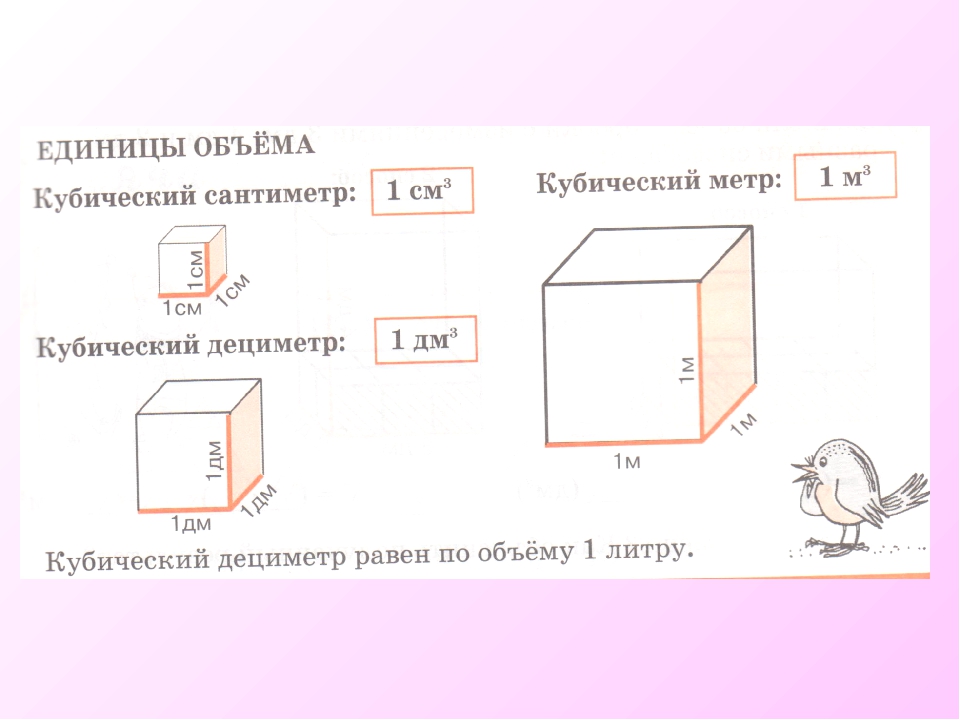
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.
Длина, ширина и высота одного кубического метра равны 10 дм
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.
Решение
a — длина
b — ширина
c — высота
a = 42 м
b = м
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
» Калькулятор
Мы смело можем заявить, что наш калькулятор является самым удобным и точным.
Мы разработали для Вас калькулятор, который быстро Вам поможет перевести необходимое вам количество кубических метров, квадратных метров или упаковок в другие единицы измерения. Возможно перевести как метры квадратные в метры кубические или упаковки, так и наоборот: метры квадратные в метры кубические и упаковки.
Возможно перевести как метры квадратные в метры кубические или упаковки, так и наоборот: метры квадратные в метры кубические и упаковки.
С помощью калькулятора можно рассчитать, сколько досок евровагонки понадобится вам для отделки конкретного количества квадратных метров поверхности.
При заказе не стоит забывать об отходах при монтаже пиломатериалов, величина которых может составлять до 10% и стоит заранее взять материалы с запасом хотя бы на 5-10%.
Если вам необходимо рассчитать кубические или квадратные метры для изделий отличных от пиломатериалов, вы можете воспользоваться нашими универсальными калькуляторами, представленными ниже.
Первый, синий калькулятор переводит из квадратных метров в кубические, вы только указываете толщину.
Второй, зеленый калькулятор переводит из кубических метров в квадратные, так же вы должны указать толщину.
Пример
Задача: Понять сколько в кубах будет доска пола толщиной 30 мм на площадь помещения 25 м2?
Решение: Вы хотите купить доску для пола толщиной 30 мм на площадь 25 м2, то есть надо перевести из квадратных метров в кубические, для этого вы в синем калькуляторе всего лишь вводите необходимую Вам площадь 25 квадратных метром и толщину половой доски 30 мм или любого предполагаемого пиломатериала, далее нажимаете кнопку рассчитать. В итоге вы получаете необходимое количество кубических метров для Вашей площади при заданной толщине.
В итоге вы получаете необходимое количество кубических метров для Вашей площади при заданной толщине.
Если Вам требуется наоборот понять сколько квадратных метров в кубе при заданной толщине, то всего лишь используйте второй, зеленый калькулятор, который делает перевод из кубических метров в квадратные.
Пользоваться калькулятором очень просто, для перевода вам необходимо всего лишь знать толщину изделия.
Можно выбрать единицы измерения толщины: миллиметры, сантиметры, дюймы и метры.
Как правильно и быстро посчитать квадратные метры стен, пола и потолка? Объём помещения по формуле, сложные фигуры
Проверить работу строителей, определить объёмы работ и материалов легко, зная как посчитать квадратные метры пола или стен помещения с помощью простых геометрических формул, несложных вычислений и нехитрых приёмов.
В строительстве и отделочных работах почти все расценки на работы сведены к стоимости за квадратный метр. Квадратура поверхностей нужна и для подсчёта расхода материала (смотрите еще: советы для дома).
Квадратура поверхностей нужна и для подсчёта расхода материала (смотрите еще: советы для дома).
Метр квадратный это сколько?
Квадратным метром называется единица измерения площади, принятая в международной системе единиц, СИ. 1м² равен площади квадрата со стороной 1 м.
Знание простых правил и нескольких геометрических формул для подсчёта количества квадратных метров стен, полов, потолка позволит избежать ошибок в вычислениях и правильно определить нужные величины.
Инструменты для подсчёта
Для замера и расчёта понадобятся следующие предметы и инструменты:
- измерительная рулетка, необходимая длина рулетки 3-5 м;
- карандаш;
- лист бумаги для записей;
- калькулятор;
- строительный угольник.
Угольником размечают перпендикуляры – линии, пересекающиеся под прямым углом.
Площадь комнаты
Знание метража комнаты пригодится для определения стоимости полового покрытия, отделки потолка, количества и мощности осветительных приборов.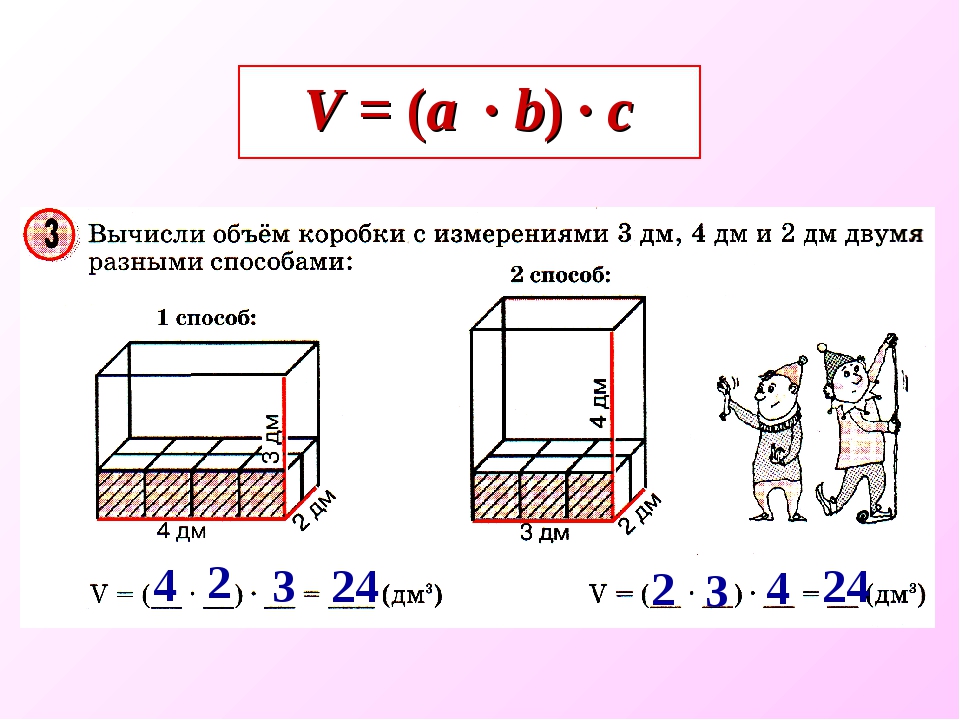 Замеряя квадратуру помещения, проверяют соответствие площади, заявленной по проекту.
Замеряя квадратуру помещения, проверяют соответствие площади, заявленной по проекту.
Измерения стен удобнее производить снизу, на уровне плинтуса. Сомнения в правильной форме помещения устраняют при помощи измерения диагоналей. Если диагонали комнаты равны, то углы – прямые, а помещение – прямоугольное.
Квадрат или прямоугольник
Самая распространенная форма комнаты в плане – квадратная или прямоугольная. Подсчёт квадратуры по полу при этом не составит особого труда:
- измеряют с помощью рулетки длину и ширину комнаты;
- перемножают цифры между собой, записывая результат на бумагу;
- выступы, колонны обмеряют, площадь элементов считают по тем же принципам, перемножая два размера;
- получившиеся цифры вычитают из площади комнаты.
При этом площадь потолка считают по тому же принципу, то есть умножают длину на ширину за вычетом технологических проемов, если таковые имеются.
[stextbox id=’warning’]Посчитав квадратные метры помещений и сложив их, можно узнать площадь всего дома. [/stextbox]
[/stextbox]
Помещение неправильной формы
Эркеры, мансарды и комнаты домов со сложной архитектурой в плане часто имеют неправильную форму. Метраж нестандартной комнаты с полукругами, выступами, множеством углов подсчитать сложнее. Облегчают задачу, используя принцип деления сложных фигур на простые.
Пол, представляя как составную фигуру мысленно или отображая на бумаге, разделяют на стандартные геометрические элементы. Затем вычисляют площадь элементов по одному и складывают полученные величины.
Г-образные, Т-образные формы помещения в плане разбивают на прямоугольники и квадраты. Полукруглые поверхности принимают как часть круга.
Количество квадратных метров пола комнаты, в основе которой лежит трапеция, можно высчитать двумя способами:
- представив трапецию, как сочетание квадрата с двумя треугольниками. Получив значение фигур, цифры складывают;
- по формуле площади трапеции.

Для подсчёта по формуле измеряют две противоположные длинные стены, эти размеры дадут значения оснований. Значение высоты определяют путём замера перпендикуляра, проведённого от одного из углов меньшего основания к большему.
Формула площади трапеции S=1/2(А+В)*Н, где:
- S – искомая величина, площадь трапеции;
- А – основание трапеции;
- В – основание трапеции;
- Н – высота трапеции.
Площадь трапециевидной комнаты – половина суммы числовых значений оснований, умноженных на высоту.
[stextbox id=’warning’]Смотрите: Как вырезать правильный угол на потолочном плинтусе?[/stextbox]
Объем комнаты
Кубатура помещения, или объём в строительстве используется при подсчёте необходимой мощности отопления, вентиляции, кондиционирования комнаты.
Объём измеряется в кубических метрах. Единица записывается как 1 м³.
С точки зрения геометрии, помещение как фигура представляет собой шестигранник.
Измерив длину, ширину и высоту комнаты прямоугольной формы, перемножив полученные измерения, получают объём простого помещения.
Объём помещения сложной формы вычисляют следующим путём:
- пол комнаты разбивают на простые геометрические фигуры;
- вычисляют квадратуру каждой фигуры;
- полученные значения складывают и умножают на высоту до потолка.
Как посчитать квадратуру стен?
Размер стены в квадратных метрах нужен для подсчёта количества отделочных материалов, размещения полок, зеркал или навесных шкафов.
Сплошная стена
Квадратура стены рассчитывается аналогично площади пола – длина, высота стены после обмера перемножаются между собой. Учитывают все впадины и выступы, если такие есть. Стены мансардных помещений под крышей часто ломаной формы, сегменты находятся в разных плоскостях.
В этом случае участки стены измеряют по отдельности, переносят на бумагу. Подсчитывают площадь каждой отдельной геометрической фигуры и суммируют числа.
С окном
Определяя количество квадратных метров стены, оконные проёмы, как правило, исключают.
Торцевые грани стен возле окна называют откосами, их размеры также не входят в метраж стены и считаются отдельно, например при подсчёте штукатурных работ или шпаклёвки.
С дверью
Квадратуру дверного проёма из площади стены при расчёте вычитают. Откосы при необходимости измеряют отдельно.
Измеряем площадь неправильной фигуры
Высчитывая метраж декоративных арочных проёмов или стрельчатых окон, поступают по тому же принципу, разбивая сложную фигуру на несколько простых элементов.
С квадратами и прямоугольниками совмещают части круга и треугольники.
Окружность
Целый круг в интерьере встречается достаточно редко. Полностью круглым может быть окно, колонны, центральная часть многоуровневого потолка. В основном дело приходится иметь с частями круга: половиной или сегментами.
Рулеткой снимают размер между двумя противоположными точками круга. Этот отрезок будет называться диаметром. Радиус круга равен половине диаметра.
Подсчёт площади круга производят по формуле S = π*R², где:
- R – радиус;
- S – площадь круга;
- π – постоянная математическая величина, округлённая до значения 3,14.
Числовое значение площади полукруга получают делением полученного результата на 2.
Квадратура сектора круга равна произведению половины длины дуги сектора на радиус круга, вычисляется по формуле S = 1/2 L*R.
Треугольник
Формула площади треугольника S=1/2*Н*А, где:
- S – площадь треугольника;
- Н – высота;
- А – сторона треугольника.
Высоту треугольника получают, измеряя рулеткой перпендикуляр от угла, противоположного к стороне.
Посмотрите на видео ниже полезные советы для быстрого и правильного подсчета квадратуры стен и пола:
[yvideo number=»9ulNrvMoO30″]
Используя простые формулы из школьного курса геометрии, можно подсчитать любую нужную величину для строительства или ремонта.
[stextbox id=’warning’]Советуем почитать: Как платить меньше за коммуналку?[/stextbox]
Статья полезна? Сохраните закладку или отметьте для друзей!
Точный расчет количества радиаторов (секций) отопления
Можно провести расчет радиаторов отопления по площади, с помощью калькулятора, размещенного на каком-либо сайте. Но данные не будут точными. Калькуляторов (программ) расчета секций радиаторов отопления много, но точную информацию можно получить только в том случае, если провести расчет вручную индивидуально для каждого помещения.
Упрощенные варианты расчета радиаторов отопления в доме
Первый способ: Расчет по объему комнат
Он прописан в положениях СНиП и применим для панельных домов, Правила предлагают в качестве нормы взять 41 Вт мощности отопления на один кубический метр отапливаемого помещения. Чтобы рассчитать количество необходимых секций достаточно объем комнаты разделить на мощность одной секции устанавливаемых радиаторов (этот параметр указывается производителем в сопроводительной технической документации).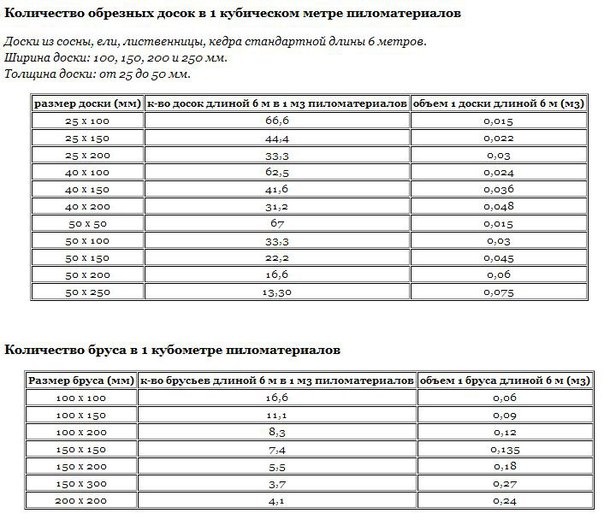
Второй способ: Расчет по площади помещений
Данный способ расчета ориентирован на помещения с потолками до 2500 мм, и за норму берется 100 Вт мощности на один квадрат площади. Для расчёта количества секций необходимо разделить площадь помещения на мощность одной секции (указывается в технической документации радиаторов).
Примерный расчет количества секций радиатора для типового помещения
N=S/P*100, где:
- N — Количество секций (дробная часть округляется по правилам математического округления))
- S — Площадь комнаты в м2
- P — Теплоотдача 1 секции, Ватт
Для этих вариантов расчета применим ряд поправок. Например, если в помещении имеется балкон, или более двух окон, или оно находится на углу здания, то к полученному количеству секций рекомендуется приплюсовать еще 20%. Если при расчете получается конечный результат (количество секций) дробное число, то его следует округлять до целого в большую сторону.
Обратите внимание: полученное значение рассчитано для идеальных условий. То есть, в доме нет дополнительных теплопотерь, сама система отопления работает эффективно, окна и двери герметично закрываются, а соседние помещения также отапливаются. В реальных условиях секций может потребоваться больше.
Точный расчет необходимого количества секций радиаторов
Выше приведены упрощенные способы расчета радиаторов, которые актуальны для типовых квартир со стандартными параметрами. С их помощью получить адекватный результат для частных жилых домов и квартир в современных новостройках нереально. Для этого следует использовать специальную формулу:
КТ = 100Вт/м2 * S * К1 * К2 * К3 * К4 * К5 * К6 * К7,
Где за основу также берется норма в 100 Вт на квадратный метр, общая площадь помещения и дополняется коэффициентами, значения которых приведены ниже:
K1 — коэффициент, учитывающий остекление оконных проемов:
- для окон с обычным двойным остеклением: 1.
 27;
27; - для окон с двойным стеклопакетом: 1.0;
- для окон с тройным стеклопакетом: 0.85;
K2 — коэффициент теплоизоляции стен:
- низкая степень теплоизоляции: 1.27;
- хорошая теплоизоляция (кладка в два крипича или слой утеплителя): 1.0;
- высокая степень теплоизоляции: 0.85;
K3 — соотношение площади окон и пола в помещении:
- 50%: 1.2;
- 40%: 1.1;
- 30%: 1.0;
- 20%: 0.9;
- 10%: 0.8;
K4 — коэффициент, позволяющий учесть среднюю температуру воздуха в самую холодную неделю года:
- для -35°C: 1.5;
- для -25°C: 1.3;
- для -20°C: 1.1;
- для -15°C: 0.9;
- для -10°C: 0.7;
K5 — корректирует потребность в тепле с учетом количества наружных стен:
- одна стена: 1.
 1;
1; - две стены: 1.2;
- три стены: 1.3;
- четыре стены: 1.4;
K6 — учет типа помещения, которое расположено выше:
- холодный чердак: 1.0;
- отапливаемый чердак: 1.0;
- отапливаемое жилое помещение: 1.0;
K7 — коэффициент, учитывающий высоту потолков:
- при 2.5 м: 1.0;
- при 3.0 м: 1.05;
- при 3.5 м: 1.1;
- при 4.0 м: 1.15;
- при 4.5 м: 1.2;
По этой формуле вы сможете рассчитать общее количества тепла, необходимого для того или иного помещения. Для определения количества секций радиаторов, вам необходимо полученный результат разделить на мощность одной секции.
Объем комнаты. Как рассчитать объем комнаты
В качестве вступления предлагаем разобраться с причинами, по которым нам может потребоваться рассчитать объем комнаты. Чаще всего сведения о количественном параметре пространства могут понадобиться:
Чаще всего сведения о количественном параметре пространства могут понадобиться:
а) при выборе и покупке домашнего кондиционера, так как эта техника подбирается исключительно на основании объема комнаты или помещения в целом;
б) при выборе и покупке домашнего отопительного радиатора, обогревающего конкретный объем комнаты;
в) при установке стационарного секционного радиатора, так как в этом случае объем комнаты будет влиять на количество необходимых секций.
При измерении объема помещения или комнаты, не помешает учитывать то, что объем измеряется кубометрами (кубическими метрами, метрами в кубе, м3), кубическими сантиметрами (сантиметр кубический, сантиметр в кубе, см3) или же литрами (в случае с жидкостями). Дополнительно можно сказать, что объем нередко ассоциируется с понятием вместимости, количеством внутреннего пространства.
Примечание: объем комнаты (м3) нередко путают с площадью комнаты (м2), что в корне неверно. Объем, в отличие от площади, величина трехмерная, учитывающая все 3 измерения:
- длину
- ширину
- высоту
Как рассчитать объем комнаты
Для выполнения необходимых вычислений нам нужно площадь комнаты помножить на высоту комнаты.
О том, как измерить площадь комнаты, мы уже говорили в статье сайта «Что Делать» под названием «Площадь комнаты. Как рассчитать площадь комнаты». Перейдя по ссылке, читатель может ознакомиться с материалом этой статьи. Тем не менее, чтобы не утруждать читателя, повторим еще раз, как рассчитывается площадь комнаты, и далее посчитаем объем комнаты:
СПОСОБ №1
1. Рассчитываем площадь:
- измеряем рулеткой длину большой стены (для простоты мерить можно по полу)
- измеряем рулеткой длину короткой стены
- умножаем первую цифру на вторую и получаем площадь (квадратуру, метры квадратные, м2)
2. Рассчитываем объем комнаты:
- измеряем высоту (расстояние от пола до потолка)
- умножаем высоту на площадь комнаты, которую мы вычислили на предыдущем этапе, получаем объем, измеряемый в кубометрах (метрах кубических, м3).
СПОСОБ №2
1. Рассчитываем объем как произведение 3-х измерений:
- измеряем по полу или стене (как будет удобней) длину большой стены
- измеряем рулеткой длину малой стены
- измеряем высоту потолков
- перемножаем 3 полученные величины и получаем тот же самый объем комнаты.

И первый, и второй способ вычисления объема комнаты дают идентичные (одинаковые) численные значения. Разница лишь в этапах выполнения расчетов.
Обязательно нужно подчеркнуть, что такие измерения годятся лишь в том случае, если комната имеет форму прямоугольного параллелепипеда. Выражаясь проще, если стены, пол и потолок комнаты представляют собою прямоугольники или же квадраты. В случае, когда нужно измерить объем комнаты, в которой есть выступы и перегородки, двухуровневый навесной потолок, альков и другие геометрические элементы, воспользуйтесь одним из советов, рассмотренных ниже.
Примечание: при выполнении измерений и расчетов, о которых будет сказано ниже, придется подключить свое воображение, мысленно разбив комнату на несколько геометрических фигур, измеряя их объемы по отдельности и суммируя полученные кубометры. Для простоты визуализации используйте распространенные формы вроде квадрата, параллелепипеда, цилиндра.
1. Измерить объем комнаты неправильной формы можно, если рассчитать площадь каждого ее элемента, сложить результаты и умножить общую площадь на высоту потолков. Аналогичная процедура описана в СПОСОБЕ №1.
Аналогичная процедура описана в СПОСОБЕ №1.
2. При измерении объема помещения, в котором имеются потолки разной высоты, нужно:
- рассчитать по отдельности объем каждой из комнат
- сложить полученные расчетные данные, получив общий объем помещения.
3. Если потолок в комнате имеет арочную форму (альков), стоит воспользоваться формулой для расчета объема цилиндра: V= Pi * R2 * H. Где:
- Н – это высота цилиндра
- R – радиус цилиндра (R2 – радиус в квадрате)
- Pi – число «Пи», равное 3,14.
Определив объем всего цилиндра (коим, конечно, альков не является), остается отнять от него примерную часть лишнего (усеченного полом) объема.
4. Зная объемы всех отдельных элементов комнаты и помещения в целом, можно посчитать общий внутренний объем, сложив вместе все полученные кубометры.
Как посчитать квадратные метры пола | Самоделки на все случаи жизни
Приведу пример расчета пола или потолка комнаты (кухни) в квадратных метрах.
Формула расчета простая, S = a*b, где S – площадь, а и b – соответственно, длина и ширина комнаты.
В нашем примере (рисунка с обмерами) вместо маленьких букв длина – А и ширина – Б., и противоположенных стен – Г и В.
Чтобы рассчитать площадь комнаты по полу:
– если у нас длина комнаты 5 метра, а ширина 3 метров, тогда нам надо ( 5*3 = 15 кв.м.), в итоге получаем 15 кв.м. по полу
Воспользуйтесь нашим Калькулятором, чтобы расчитать площадь пола или потолка
Если вы не хотите в ручную рассчитывать площадь пола или вы, что то не поняли при описание расчетов, то вы можете воспользоваться нашим калькулятором и рассчитать площадь пола или потолка автоматически.
Для расчёта необходимо измерить в метрах длину, ширину комнаты и внести данные по порядку заполнив форму и вы автоматически получите расчет площади пола или потолка в квадратных метрах.
Калькулятор расчёта площади пола
Примечание:
Обращаем ваше внимание, что измерения необходимо проводить в метрах. Т.е. если вы получили длину комнаты 964 сантиметров, то в поля формы необходимо ввести значение 9.64. Обратите внимание, что дробные числа нужно вводить с точкой, а не с запятой!
Т.е. 2,6 — неправильно , 2.6 — правильно
Калькулятор рассчитывает не только площадь пола или потолка, данный калькулятор можно также использовать для расчёта площади любых других прямоугольных объектов у которых есть длина и ширина. В этом случае вместо ширины и длины комнаты вам необходимо подставить значения ширины и длины этих самых объектов (окна, двери и т.д.,) к примеру таких как площадь окон и дверей.
К примеру как можно проверить и расчитать в ручную площадь окон и дверей.:
– если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров.
– а двери ширина 0,8 метров, а высота 2,05 метров.
Окно: (1,6*1,5)= 2,4 кв.м., в итоге окно получаем 2,4 кв.м.,
Двери: (0,8*2,05)= 1,64 кв.м, в итоге двери получаем 1,64 кв.м.,
Чтобы рассчитать площадь комнаты по стенам: воспользуйтесь нашим Калькулятором, чтобы расчитать площадь стен
Как посчитать квадратуру комнаты, стен, потолка, пола
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.
Часто требуется посчитать кубатуру комнаты, ее объем
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения.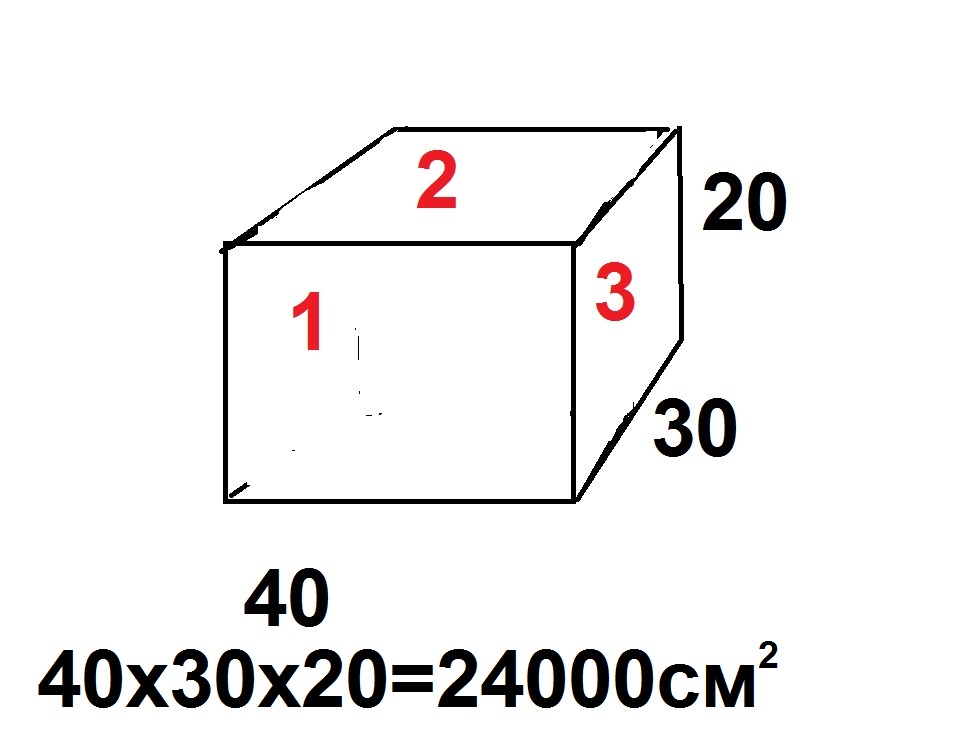 Для этого нужны будут:
Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Как высчитать площадь комнаты
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Площадь комнаты сложной формы
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв.
 м.
м. - Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
Как посчитать площадь комнаты неправильной формы
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв.
 м. После округления получаем 1,2 кв. м.
м. После округления получаем 1,2 кв. м. - Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Формулы расчета площади и периметра простых геометрических фигур
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
Удобнее всего размеры наносить на план
Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,75 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв. м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты
Формула расчета объема комнаты
Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м 3 . Итак, объем помещения 44,8 куба.
Как рассчитать квадратный метр пола и зачем это нужно
Каждая из частей, из которых состоит любое здание, имеет свои поверхности, большинство из них имеют названия, например, стена, пол, потолок.
При выполнении строительных работ, будь то строительство нового дома или ремонт старого, требуется количественная оценка размеров таких поверхностей.
Ее и принято называть – площадь. Чаще всего размеры этих площадей нужны для отделочных работ, так как изготовитель материалов указывает их норму расхода на этикетках, в виде надписей на упаковках, а также в отдельно прилагаемых инструкциях.
Норма расхода – количество материала, требуемое для отделки единичной площади, которая обычно принимается размером в квадратный метр. Потребителю нужно всего лишь перемножить норму расхода на величину отделываемой площади для того, чтобы узнать общее количество требуемого материала в килограммах, мешках, банках или штуках.
Основные понятия
Для того чтобы рассчитать площади таких поверхностей, как полы, потолки и стены, посмотрим на них и обнаружим, что они состоят из базовых геометрических фигур: четырехугольник, треугольник и окружность или из их сочетаний.
Рассчет площади полам
Обратимся к школьным урокам геометрии и вспомним, как рассчитываются эти геометрические фигуры.
Четырехугольники
К ним относятся такие фигуры, как:
- прямоугольник, все его четыре угла прямые, а противоположные стороны равны между собой, его частным случаем является квадрат, у которого равны все четыре стороны
- четырехугольник, со всеми сторонами разного размера
- параллелограммы, с попарно параллельными сторонами, две из которых сдвинуты относительно друг друга, его частным случаем является ромб, у которого все четыре стороны имеют одинаковый размер
- трапеции, четырехугольники с двумя противоположными параллельными сторонами, одна из которых меньше другой
Треугольники
Треугольники имеют три стороны и три вершины, они бывают:
- прямоугольными, то есть две стороны соединяются друг с другом под прямым углом
- со сторонами разного размера
Окружности
Это замкнутый криволинейный контур, который может быть в виде:
- правильного круга с постоянной величиной радиуса или диаметра
- в виде эллипса, сплюснутого с двух сторон круга
- сегменты, части кругов или эллипсов, имеющие одну сторону в виде прямой линии — хорды, а другую криволинейную
Объемные криволинейные фигуры
Криволинейная площадь пола
Эти фигуры очень редко используются целиком, но достаточно популярны их части в виде объемных сегментов:
Расчет геометрических фигур
Площадь четырехугольника
Вид четырехугольника обычно имеют стены, потолки, полы, дверные и оконные проемы.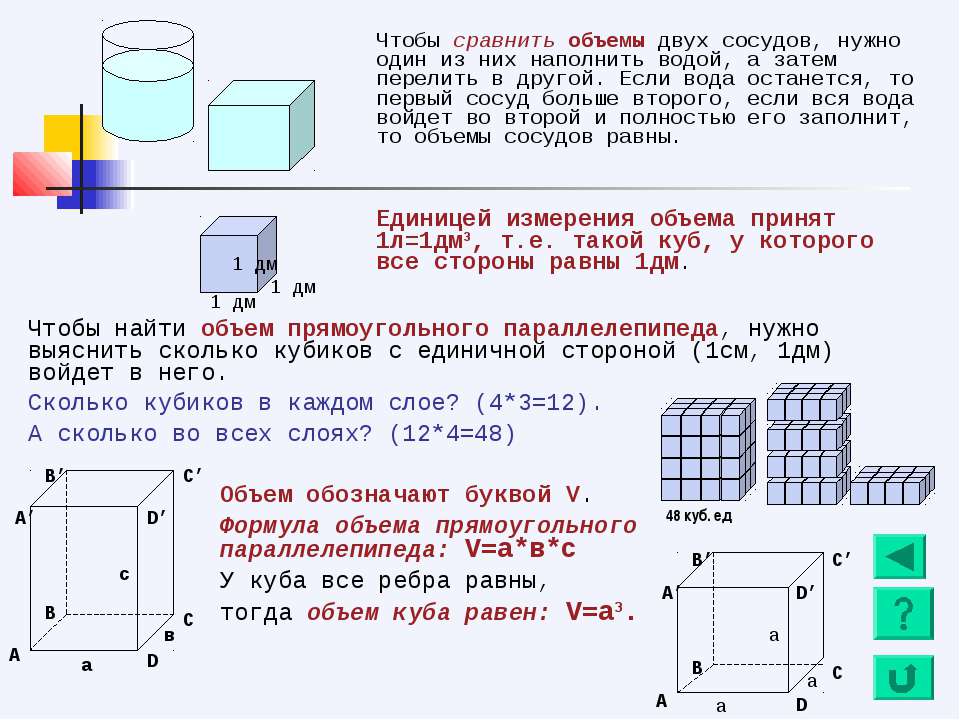
Проще всего вычислить площадь прямоугольника или квадрата. Для этого нужно всего лишь перемножить размеры двух его перпендикулярных сторон, их еще называют длина и ширина, если прямоугольник горизонтальный, или длина и высота, если он располагается вертикально.
По разным причинам, не всегда четырёхугольные поверхности в доме имеют прямые углы и одинаковые стороны. Для расчёта площади «S» такого четырехугольника имеется специальная формула:
S = √ ( p − a ) ( p − b ) ( p − c ) ( p − d ) , где:
- a, b, c, d — длины сторон прямоугольника
- p = (a + b + c + d) / 2 — полупериметр
Площадь параллелограмма или его частного случая ромба вычисляется перемножением длины одной из параллельных сторон с геометрической высотой, то есть длиной линии, проведенной из одной его вершины перпендикулярно противоположной параллельной стороне до пересечения с ней.
Если это трапеция, ее площадь вычисляется как половина суммы размеров параллельных сторон, умноженная на расстояние между ними (геометрическую высоту).
Иметь план в виде трапеции могут ниши в стенах или выступающие за границы фасада эркеры.
Площадь треугольника
Треугольными бывают фронтоны здания, поверхности скатов кровли, эркеры или ниши. С одним прямым углом – это половина произведения его катетов (меньших сторон). С произвольной длиной сторон равна половине величины, получаемой умножением размера одной из сторон на геометрическую высоту (перпендикуляра, опущенного на эту сторону из противолежащего угла).
Площадь окружности
Площадь круга вычисляется по формуле:
S = Пи * R * R, где:
- Пи – числовая константа, равная 3.1415
- R – радиус круга
Площадь эллипса
У эллипса линии, делящие эллипс на 4 равных части, называется не диаметром как у круга, а осями – большой (a) и малой (b). Формула для расчета его площади:
S = Пи * (a * b) / 4, где:
- Пи – числовая константа, равная 3.1415
- a – большая ось эллипса
- b – малая ось эллипса
Площадь сегмента круга или эллипса
S = [(R * R) / 2] * (a –sin a), где:
Если радиус неизвестен, он вычисляется по формуле:
R = (h / 2) + [(c * c) / (8 * h)], а угол a по формуле:
a = 2 * arcsin [c / (2 * R)], где:
- R – радиус
- h – геометрическая высота сегмента
- c – длина хорды
Окружность сегмента
Для ее вычисления возьмем формулу:
L =a * R, где:
- L – дуга сегмента
- R – радиус
- а – угол сегмента
Вычисление площадей стен, полов и потолков
Стены
Если поверхность стены однородна и не имеет никаких вырезанных частей в виде проемов, ее площадь вычисляется по одной из формул для четырехугольников, которому она больше всего соответствует. Когда в стене имеются выступающие части (например, печь, камин) или части, выходящие за ее пределы, но составляющие с ней одно целое (например, ниши или эркеры), площадь их вертикальных проекций вычитается или, наоборот, добавляется к ранее вычисленной.
Когда в стене имеются выступающие части (например, печь, камин) или части, выходящие за ее пределы, но составляющие с ней одно целое (например, ниши или эркеры), площадь их вертикальных проекций вычитается или, наоборот, добавляется к ранее вычисленной.
Площадь стены с камином
Допустим, что стена имеет два проема – прямоугольный оконный и арочный (состоит из прямоугольника и сегмента, приставленного к нему сверху). У этой же стены расположен прямоугольный камин, а также полукруглая ниша и эркер, который в плане имеет вид трапеции. Из площади стены, рассчитанной как четырехугольник нужно вычесть площади проемов прямоугольного и арочного, а также площадь прямоугольной проекции камина.
То есть нужно рассчитать площади трех прямоугольников и одного сегмента, а затем вычесть их из площади стены. Полукруглая ниша и эркер в плоскости стены тоже имеют вид прямоугольников и их площади также вычитаются из площади стены. Затем можно посчитать площади частей стены, образующих нишу и эркер.
Для ниши – вычисляется длина ее дуги и умножается на ее высоту. Для эркера с основанием в виде трапеции – измеряются длины ее сторон, за исключением самой большой, совпадающей с плоскостью стены и тоже умножаются на его высоту.
Полученные результаты нужно прибавить к площади стены и тогда с достаточно высокой точностью узнать ее вычисленную площадь.
Полы и потолки
Площади пола и потолка рассчитываются путем вычитания или сложения с их четырехугольной поверхностью площадей врезанных или выступающих частей. Для вышеприведенного примера это будут – прямоугольная горизонтальная проекция камина, основание эркера в виде трапеции и ниши в виде сегмента. Таким образом, из базовой площади пола или потолка нужно вырезать площадь одного прямоугольника, и прибавить площади трапеции и сегмента.
При оформлении потолка вторым уровнем на нем может быть закреплен элемент в виде круга или эллипса. Для определения его площади следует воспользоваться соответствующими формулами для их расчета.
Расчет всегда должен производиться в одних и тех же единицах – лучше, если это будут квадратные метры. Никогда не следует смешивать в одном и том же расчете метры, сантиметры и миллиметры.
Как рассчитать линолеум — на видео:
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.
Как рассчитать площадь пола в помещениях разной формы – примеры
Невозможно проводить ремонт напольной поверхности, не зная точную площадь пола в частном домовладении или квартире. Дело в том, что сегодня стоимость строительных материалов достаточно высокая, и каждый владелец недвижимости старается максимально сэкономить на их покупке. Поэтому информация, как рассчитать площадь пола, не будет лишней для того, кто предпочитает делать ремонт собственноручно.
Зачем нужно знать площадь пола
Прежде чем приступить к работе, следует определиться с объемом мероприятий, запланировать затраты и рассчитать количество стройматериалов. Для этого нужны будут исходные данные. По этой причине важно знать, как посчитать площадь пола безошибочно. Особенно это касается неровных поверхностей и помещений, имеющих нестандартную планировку.
Для этого нужны будут исходные данные. По этой причине важно знать, как посчитать площадь пола безошибочно. Особенно это касается неровных поверхностей и помещений, имеющих нестандартную планировку.
Встречаются и другие причины, когда имеется потребность точно определить размеры поверхности пола:
- проверка качества выполнения строительных работ;
- необходимость проведения перепланировки помещения.
В данной статье рассказывается, как посчитать площадь пола в квадратных метрах в комнатах, имеющих разную конфигурацию.
Определение площади прямоугольного помещения
До того, как высчитать площадь пола, следует запастись калькулятором и измерительной рулеткой. Чаще всего встречаются комнаты в форме прямоугольника. Для вычисления их площади пользуются формулой, известной всем со школы: S = a х b, где a и b – длина и ширина. Например, у помещения параметры 3 и 4 метра, тогда искомая величина составит 12 кв. м.
В том случае, когда в комнате имеется камин или встроенные предметы мебели, тогда нужно узнать их площадь и вычесть из общей площади. В случае проведения капитального ремонта пола, все лишнее в помещении придется демонтировать.
В случае проведения капитального ремонта пола, все лишнее в помещении придется демонтировать.
Расчет площади комнаты неправильной планировки
Намного труднее вычислить площадь комнаты, имеющей многоугольную форму. Часто в кирпичных домах в планировке присутствуют ниши, треугольные углубления и округлые элементы, как на фото.
В данном случае, прежде, как посчитать квадратуру пола, схему помещения надо разбить на отдельные зоны. Например, если комната имеет Г-образную планировку, ее следует поделить на 2 прямоугольника, после чего подсчитать площадь каждого из них и полученные результаты сложить.
Узнаём площадь треугольного помещения
Когда другая часть комнаты располагается не перпендикулярно относительно основной площади, это означает, что между двумя прямоугольниками присутствует еще и треугольник, имеющий прямой угол.
В данном случае площадь треугольника вычисляют по формуле: S = (a х b):2 и прибавляют к общему итогу. Например, а = 2, b = 3, тогда S = (2х3): 2 =3 м².
Можно иначе определить площадь:
- Прежде вычисляют квадрату прямоугольника.
- Определяют площадь скошенного треугольного угла.
- Из квадратуры прямоугольника вычитают площадь треугольника.
В том случае, когда треугольник не имеет прямого угла, тогда используют формулу Герона S = √p(p – a)(p – b)(p – c).
Например, стороны его равны 5, 6 и 7 метров, тогда вычисления производят следующим образом:
- Узнают полупериметр треугольника p = (5+6+7):2 = 9.
- В формулу Герона подставляют цифровые значения и получают результат: √(9 х(9-7) х(9-6)х(9-5) =14,7 м².
Квадратура помещений округлой формы
Нередко подобная форма присутствует у окон в домах старой постройки или на балконах, которые совмещены с комнатами. Сначала вычисляют 1/2 выступающей части окружности и добавляют к площади прямоугольника, применяя формулу S = πR²:2, в которой:
R² – радиус круга, возведенный в квадрат.
Например, в комнате имеется выступающий балкон полукруглой формы с радиусом 1,5 метра. Подставив данное число в формулу, получаем результат: S = 3,14х(1,5)²: 2 =3,5 м². Читайте также: “Как посчитать квадратные метры пола при разной форме комнат”.
Подставив данное число в формулу, получаем результат: S = 3,14х(1,5)²: 2 =3,5 м². Читайте также: “Как посчитать квадратные метры пола при разной форме комнат”.
Как рассчитать площадь стен комнаты
Порядок вычисления площади стенок и пола отличается. Дело в том, что до того, как рассчитать квадратуру пола, следует узнать длину и ширину помещения, а для расчета стен потребуется измерить его высоту. Поэтому сначала узнают периметр комнаты и умножают на высоту потолков.
Например, параметры пола 3 и 4 метра, а высота помещения равна 3 метрам. В этом случае периметр стен будет равен (3 + 4) х2 = 14 м., а их площадь S = 14х3 = 42 м².
При этом не следует забывать про квадратуру проемов окон и дверей. Их площадь вычитают после завершения расчетов стен. Но с другой стороны их можно не принимать во внимание и тем самым обеспечить некоторый запас материалов.
Пропорции между площадью пола и окон
Чтобы обеспечить качественное проведение ремонта нужно заранее выяснить, как вычислить площадь пола и другие необходимые размеры помещения. Подготовительный этап также предусматривает приобретение стройматериалов и тогда в процессе ремонта затраты будут сведены к минимуму, поскольку не получится больших остатков и стоимость доставки обойдется недорого.
Подготовительный этап также предусматривает приобретение стройматериалов и тогда в процессе ремонта затраты будут сведены к минимуму, поскольку не получится больших остатков и стоимость доставки обойдется недорого.
Ручной способ вычислений как узнать площадь пола займет больше времени, чем при проведении расчетов на уже имеющемся строительном калькуляторе, но он позволяет узнать более точные результаты.
Как правильно и быстро посчитать квадратные метры стен, пола и потолка? Объём помещения по формуле, сложные фигуры
Проверить работу строителей, определить объёмы работ и материалов легко, зная как посчитать квадратные метры пола или стен помещения с помощью простых геометрических формул, несложных вычислений и нехитрых приёмов.
В строительстве и отделочных работах почти все расценки на работы сведены к стоимости за квадратный метр.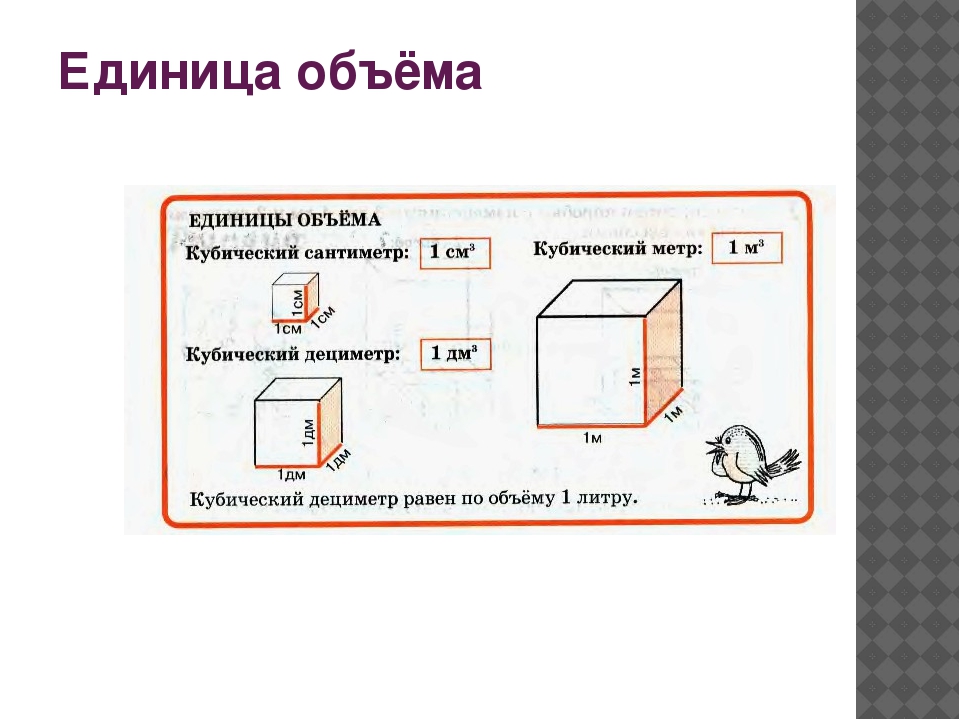 Квадратура поверхностей нужна и для подсчёта расхода материала.
Квадратура поверхностей нужна и для подсчёта расхода материала.
Метр квадратный это сколько?
Квадратным метром называется единица измерения площади, принятая в международной системе единиц, СИ. 1м² равен площади квадрата со стороной 1 м.
Знание простых правил и нескольких геометрических формул для подсчёта количества квадратных метров стен, полов, потолка позволит избежать ошибок в вычислениях и правильно определить нужные величины.
Инструменты для подсчёта
Для замера и расчёта понадобятся следующие предметы и инструменты:
- измерительная рулетка, необходимая длина рулетки 3-5 м;
- карандаш;
- лист бумаги для записей;
- калькулятор;
- строительный угольник.
Угольником размечают перпендикуляры – линии, пересекающиеся под прямым углом.
Площадь комнаты
Знание метража комнаты пригодится для определения стоимости полового покрытия, отделки потолка, количества и мощности осветительных приборов. Замеряя квадратуру помещения, проверяют соответствие площади, заявленной по проекту.
Замеряя квадратуру помещения, проверяют соответствие площади, заявленной по проекту.
Измерения стен удобнее производить снизу, на уровне плинтуса. Сомнения в правильной форме помещения устраняют при помощи измерения диагоналей. Если диагонали комнаты равны, то углы – прямые, а помещение – прямоугольное.
Квадрат или прямоугольник
Самая распространенная форма комнаты в плане – квадратная или прямоугольная. Подсчёт квадратуры по полу при этом не составит особого труда:
- измеряют с помощью рулетки длину и ширину комнаты;
- перемножают цифры между собой, записывая результат на бумагу;
- выступы, колонны обмеряют, площадь элементов считают по тем же принципам, перемножая два размера;
- получившиеся цифры вычитают из площади комнаты.
При этом площадь потолка считают по тому же принципу, то есть умножают длину на ширину за вычетом технологических проемов, если таковые имеются.
Помещение неправильной формы
Эркеры, мансарды и комнаты домов со сложной архитектурой в плане часто имеют неправильную форму. Метраж нестандартной комнаты с полукругами, выступами, множеством углов подсчитать сложнее. Облегчают задачу, используя принцип деления сложных фигур на простые.
Метраж нестандартной комнаты с полукругами, выступами, множеством углов подсчитать сложнее. Облегчают задачу, используя принцип деления сложных фигур на простые.
Пол, представляя как составную фигуру мысленно или отображая на бумаге, разделяют на стандартные геометрические элементы. Затем вычисляют площадь элементов по одному и складывают полученные величины.
Г-образные, Т-образные формы помещения в плане разбивают на прямоугольники и квадраты. Полукруглые поверхности принимают как часть круга.
Количество квадратных метров пола комнаты, в основе которой лежит трапеция, можно высчитать двумя способами:
- представив трапецию, как сочетание квадрата с двумя треугольниками. Получив значение фигур, цифры складывают;
- по формуле площади трапеции.
Для подсчёта по формуле измеряют две противоположные длинные стены, эти размеры дадут значения оснований. Значение высоты определяют путём замера перпендикуляра, проведённого от одного из углов меньшего основания к большему.
Формула площади трапеции S=1/2(А+В)*Н, где:
- S – искомая величина, площадь трапеции;
- А – основание трапеции;
- В – основание трапеции;
- Н – высота трапеции.
Площадь трапециевидной комнаты – половина суммы числовых значений оснований, умноженных на высоту.
Объем комнаты
Кубатура помещения, или объём в строительстве используется при подсчёте необходимой мощности отопления, вентиляции, кондиционирования комнаты.
Объём измеряется в кубических метрах. Единица записывается как 1 м³.
С точки зрения геометрии, помещение как фигура представляет собой шестигранник.
Измерив длину, ширину и высоту комнаты прямоугольной формы, перемножив полученные измерения, получают объём простого помещения.
Объём помещения сложной формы вычисляют следующим путём:
- пол комнаты разбивают на простые геометрические фигуры;
- вычисляют квадратуру каждой фигуры;
- полученные значения складывают и умножают на высоту до потолка.

Как посчитать квадратуру стен?
Размер стены в квадратных метрах нужен для подсчёта количества отделочных материалов, размещения полок, зеркал или навесных шкафов.
Сплошная стена
Квадратура стены рассчитывается аналогично площади пола – длина, высота стены после обмера перемножаются между собой. Учитывают все впадины и выступы, если такие есть. Стены мансардных помещений под крышей часто ломаной формы, сегменты находятся в разных плоскостях.
В этом случае участки стены измеряют по отдельности, переносят на бумагу. Подсчитывают площадь каждой отдельной геометрической фигуры и суммируют числа.
С окном
Определяя количество квадратных метров стены, оконные проёмы, как правило, исключают.
Торцевые грани стен возле окна называют откосами, их размеры также не входят в метраж стены и считаются отдельно, например при подсчёте штукатурных работ или шпаклёвки.
С дверью
Квадратуру дверного проёма из площади стены при расчёте вычитают.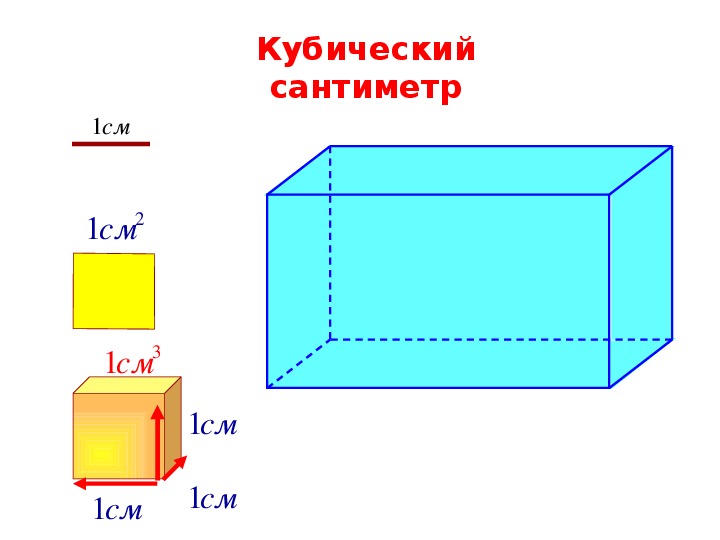 Откосы при необходимости измеряют отдельно.
Откосы при необходимости измеряют отдельно.
Измеряем площадь неправильной фигуры
Высчитывая метраж декоративных арочных проёмов или стрельчатых окон, поступают по тому же принципу, разбивая сложную фигуру на несколько простых элементов.
С квадратами и прямоугольниками совмещают части круга и треугольники.
Окружность
Целый круг в интерьере встречается достаточно редко. Полностью круглым может быть окно, колонны, центральная часть многоуровневого потолка. В основном дело приходится иметь с частями круга: половиной или сегментами.
Рулеткой снимают размер между двумя противоположными точками круга. Этот отрезок будет называться диаметром. Радиус круга равен половине диаметра.
Подсчёт площади круга производят по формуле S = π*R², где:
- R – радиус;
- S – площадь круга;
- π – постоянная математическая величина, округлённая до значения 3,14.
Числовое значение площади полукруга получают делением полученного результата на 2.
Квадратура сектора круга равна произведению половины длины дуги сектора на радиус круга, вычисляется по формуле S = 1/2 L*R.
Треугольник
Формула площади треугольника S=1/2*Н*А, где:
- S – площадь треугольника;
- Н – высота;
- А – сторона треугольника.
Высоту треугольника получают, измеряя рулеткой перпендикуляр от угла, противоположного к стороне.
Посмотрите на видео ниже полезные советы для быстрого и правильного подсчета квадратуры стен и пола:
Статья полезна? Сохраните закладку или отметьте для друзей!
”
Как измерить кубические футы в минуту и расход воздуха — ISC Sales
Когда вы смотрите на промышленные товары, как узнать, сколько CFM нужно переместить? Что такое кубических футов в минуту? Как вы измеряете размер своей комнаты? Правильная вентиляция важна в любой среде, но еще важнее в промышленных условиях. Правильное количество «свежего воздуха» может быть разницей между здоровой и нездоровой рабочей средой.
Правильное количество «свежего воздуха» может быть разницей между здоровой и нездоровой рабочей средой.
Измерить и понять CFM не так сложно, как вы думаете.
ЗНАЕТЕ ЛИ ВЫ:
Высококачественные воздушные фильтры класса MERV-13 и выше помогают фильтровать вредные вирусы, бактерии и аллергены из воздуха, которым вы дышите.
Что такое CFM?
CFM означает кубических футов в минуту и является наиболее распространенным способом измерения расхода воздуха. Площадь измеряется в квадратных единицах (например, квадратных футах). Объемы (например, комната, наполненная воздухом) измеряются в кубических единицах — CFM определяет, сколько кубических футов можно перемещать или обменивать каждую минуту.
Помещению размером 1000 футов³ потребуется система на 1000 кубических футов в минуту для замены всего воздуха каждую минуту.
Как измерить объем комнаты?
Многие комнаты представляют собой простые коробки или прямоугольные призмы . Объем определяется как длина × ширина × высота . Комната 100 футов в длину, 50 футов в ширину и 20 футов в высоту имеет размер 100 000 футов³ (100 × 50 × 20 = 100 000).
Объем определяется как длина × ширина × высота . Комната 100 футов в длину, 50 футов в ширину и 20 футов в высоту имеет размер 100 000 футов³ (100 × 50 × 20 = 100 000).
Некоторые помещения имеют неровные стены, наклонные потолки или другие особенности, которые затрудняют их измерение.Не волнуйтесь — сложные формы можно разделить на простые, которые нужно измерить, а затем снова объединить измерения для получения общей суммы.
В примере, показанном справа, площадь этой комнаты неправильной формы можно измерить, сначала измерив пространство A (50 × 50 = 2500 футов²), а затем прибавив это значение к пространству B (20 ′ × 30 ′ = 600 фут²). Номер общей площадью 3100 кв. М.
Чтобы получить объем любой формы, просто умножьте общую площадь на среднюю высоту (не показано на нашем простом чертеже).
Как часто мне нужно менять воздух?
Теперь, когда вы знаете объем воздуха в вашем помещении, вам нужно определить, как быстро он должен быть заменен.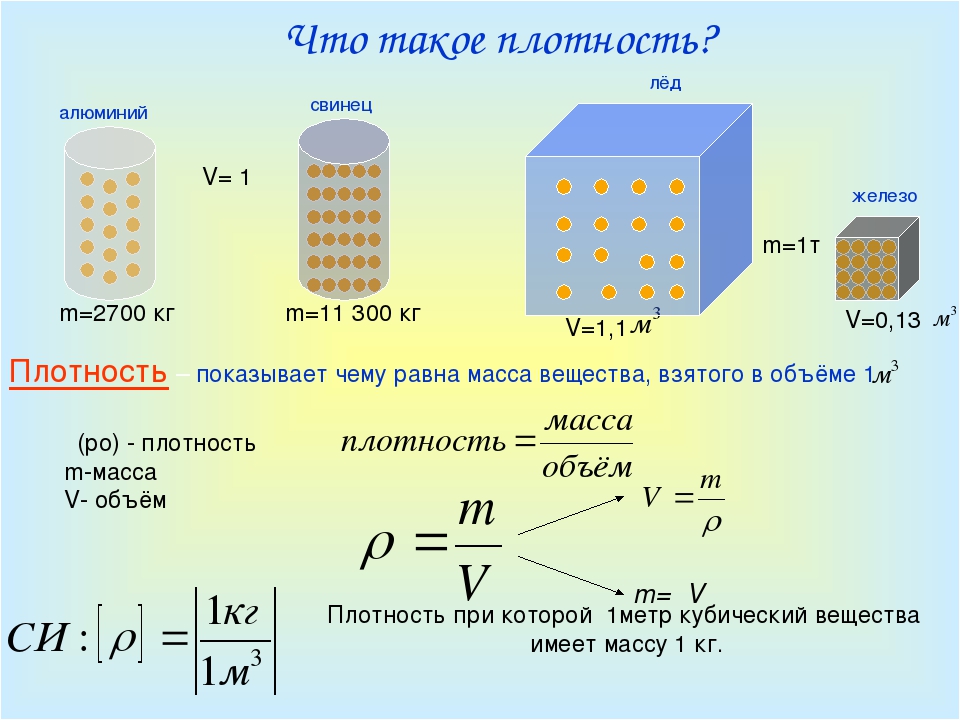 Конкретные требования к воздушному потоку зависят от вашей конкретной настройки, но вот несколько общих примеров рекомендуемых обменных курсов:
Конкретные требования к воздушному потоку зависят от вашей конкретной настройки, но вот несколько общих примеров рекомендуемых обменных курсов:
Машинное отделение, генераторное отделение, котельная — каждые 1-4 минуты
В этих помещениях есть потенциально опасные выхлопные газы, которые необходимо быстро удалить, поэтому весь воздух следует циклировать каждые 1-4 минуты.Если у вас есть машинное отделение объемом 2000 кубических футов, вам понадобится система, способная перемещать 500–2000 кубических футов в минуту.
Кухня, кафетерий, пекарня, бар, лаборатория — каждые 2-5 минут
В лабораториях и помещениях для приготовления или подачи пищи обычно требуется умеренная или сильная циркуляция воздуха (примерно каждые 2-5 минут). Для области или лаборатории, связанной с пищевыми продуктами, площадью 2000 футов³ вам может потребоваться система, способная обрабатывать приблизительно 400-1000 кубических футов в минуту.
Склад, производственный цех, механический цех, завод — каждые 3-7 минут
Хотя это не так интенсивно, как машинные отделения или пищевые помещения, в большинстве промышленных зон по-прежнему требуется постоянный поток воздуха для удаления паров, связанных с работой, и для поддержания чистоты воздуха.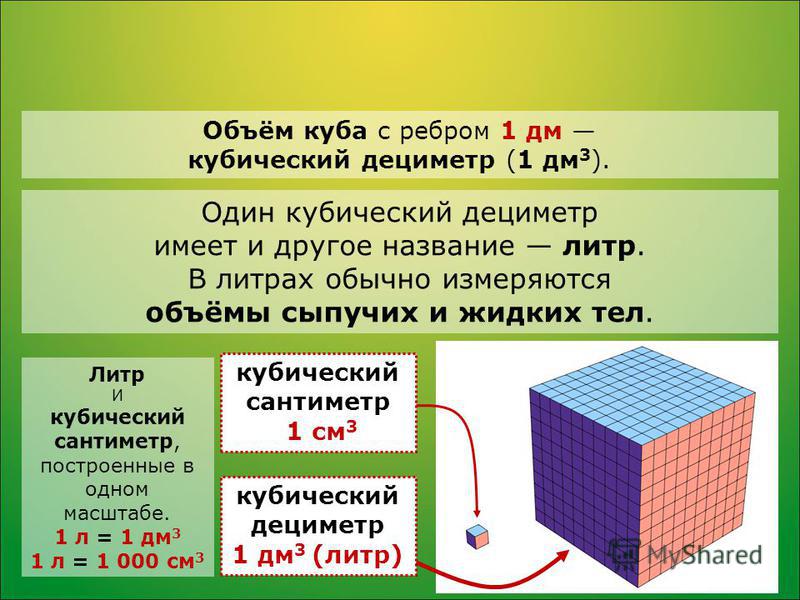 Например, для промышленной зоны площадью 2 000 футов3 обычно требуется система, способная выдавать 280-670 кубических футов в минуту.
Например, для промышленной зоны площадью 2 000 футов3 обычно требуется система, способная выдавать 280-670 кубических футов в минуту.
Класс, Дом, Офис, Магазин, Спортзал, Туалет, Аудитория — каждые 4-10 минут
Дома и общественные места, такие как конференц-залы, магазины розничной торговли и офисы, немного менее требовательны, чем другие типы помещений, упомянутые выше. Для этих помещений воздухообмен обычно не так критичен, и для помещения площадью 2000 футов3 потребуется система, способная перемещаться на 200-500 кубических футов в минуту.
Сколько мне нужно CFM?
После того, как вы определили объем вашего пространства и решили, как быстро вам нужно будет заменить воздух в комнате, вы можете рассчитать CFM, необходимый для вашей системы.
Начните с общего объема воздуха (в кубических футах), разделите на коэффициент обмена (как быстро вы хотите заменить воздух), и в результате получите общий CFM, необходимый для вашей системы.
Имейте в виду, что во многих приложениях (особенно на больших площадях) используется более одного вентилятора / нагнетателя.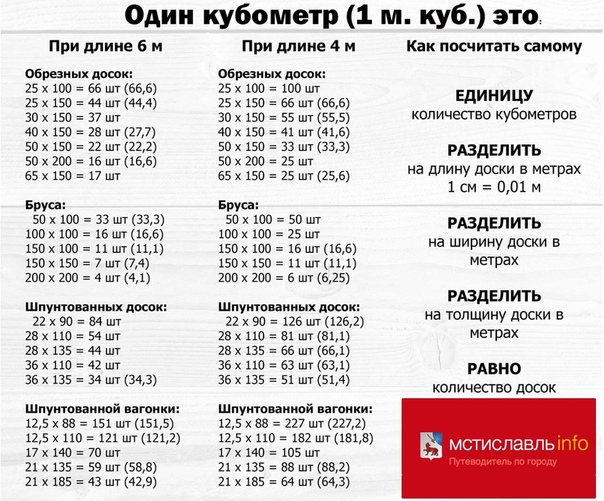 Часто имеет смысл использовать много меньших единиц, а не одну большую единицу для обработки всего CFM.
Часто имеет смысл использовать много меньших единиц, а не одну большую единицу для обработки всего CFM.
Заключение
Видите? Измерение кубических футов в минуту не так сложно, как вы думаете: просто измерьте объем комнаты и разделите на то, насколько быстро вы хотите заменить воздух, и все!
Теперь, когда у вас есть лучшее представление о том, какой CFM вам нужен, вы можете принимать более обоснованные решения при покупке таких предметов, как вентиляторы, испарительные охладители или переносные нагреватели.
Продолжить чтение: Вам также может понравиться наша статья о последнем руководстве по воздушным фильтрам, которые вам когда-либо понадобятся!
Позвоните в отдел продаж ISC сегодня по телефону 877.602.0010 , чтобы получить бесплатное предложение или узнать о нашей линейке промышленного оборудования. Вы также можете запросить коммерческое предложение онлайн, ЗДЕСЬ .
Как своевременно получать частицы на кубический метр
| в SmartScan | Теджиндер Сингх
Стандарты ISO 14644 для мониторинга чистых помещений требуют измерения частиц в воздухе в количестве частиц на кубический метр.Большинство счетчиков частиц, используемых для этих целей, имеют скорость потока пробы, которая внутренне регулируется до одного кубического фута в минуту (1 куб. Фут / мин). Поскольку образец размером в один кубический метр содержит 35,3 кубических фута, для накопления образца объемом в один кубический метр требуется немного больше 35,3 минут (2118 секунд). Между обновлениями проходит довольно много времени.
Все станции удаленного мониторинга SmartScan DA-07 имеют несколько массивов из 36 элементов для каждого удаленного устройства. Их можно использовать для накопления количества частиц на кубический метр для каждого размерного канала в удаленном счетчике частиц.На диаграмме ниже показана структура одного из массивов вместе с тремя другими переменными, которые будут использоваться для управления накоплением счетчика.
«Индекс» определяет, какой из 36 элементов массива получит следующую информацию отсчета от счетчика частиц. «Сумма» используется для накопления количества частиц на кубический метр, а «Счетчик» увеличивается для каждой пробы, пока не достигнет «36», указывающего, что массив заполнен. (Тридцать шесть (36) проб размером один кубический фут означает, что для каждого значения частиц на кубический метр будет отобрано чуть более одного метра.Это было выбрано из соображений консервативности и обеспечения выхода наихудшего случая.) Во время счета до 36 операция накопления продолжается, как показано на диаграмме ниже.
Значение «Индекса» говорит о том, что следующим будет обработан элемент массива номер 3. Когда следующее измерение в кубических футах получено от счетчика частиц, оно сохраняется в массиве в соответствии с «Индексом» и добавляется к значению «Сумма» (операции №1 и №2). «Счетчик» также увеличивается (# 3), если он меньше 36. Это продолжается до тех пор, пока «Счетчик» не достигнет 36, что указывает на то, что массив заполнен, а «Сумма» затем содержит действительное значение частиц на кубический метр.
Это продолжается до тех пор, пока «Счетчик» не достигнет 36, что указывает на то, что массив заполнен, а «Сумма» затем содержит действительное значение частиц на кубический метр.
Когда массив заполнится («Счетчик достигает 36»), начинается операция накопления, как показано на диаграмме ниже.
Как и раньше, «Индекс» указывает на элемент массива, который будет обрабатываться следующим. Когда новое измерение доступно со счетчика частиц, старое измерение из массива вычитается из «Суммы» (№1 на диаграмме) до того, как входящее значение сохраняется в массиве (№2) и добавляется к «Сумме. »(№3).Затем «Индекс» увеличивается до следующего элемента массива (# 4). (Обратите внимание, что когда «Индекс» достигает конца массива, он автоматически возвращается к началу для следующего измерения. Это называется «круговым буфер »)
После заполнения массива данные о количестве частиц на кубический метр отправляются на сервер один раз в минуту.
Получите уверенность в мониторинге критически важных приложений в любом месте и в любое время. Выберите систему мониторинга чистых помещений SmartScan сегодня.
Выберите систему мониторинга чистых помещений SmartScan сегодня.
Как посчитать кубические метры
Вам когда-нибудь приходилось знать объем ящика, лестницы или аквариума? Если вам нужно заполнить некоторые пространства или вы хотите окрасить всю новую студию в свой любимый цвет, вам нужно будет измерить кубические метры. Есть много способов рассчитать кубический размер трехмерного пространства. Вам нужно взять рулетку и рассчитать длину, ширину и высоту вашей комнаты. Если вы уже знаете квадратные метры вашей комнаты, вам просто нужно вычислить высоту и умножить их вместе.
Важно знать, что все измерения должны быть в одних и тех же единицах, чтобы это работало. Если длина и ширина указаны в метрах, а высота — в сантиметрах, необходимо преобразовать сантиметры в метры или наоборот. Метры, футы, дюймы, если они все одинаковы, вы рассчитаете правильные кубические метры.
Кубический материал — это обозначение объема. Он измеряет количество, которое что-то может удерживать. Знание кубических метража может помочь вам в принятии решения о покупке определенных объектов.Чтобы избежать возможных заблуждений, таких как покупка стиральной машины или холодильника, который смотрел в магазине, что он идеально впишется в ваш дом, вы должны знать перед покупкой кубические метры доступного пространства, которое у вас есть в вашем доме. Если случится так, что никто не спросит спецификации продукта, который вы собираетесь купить, вы всегда можете взять с собой мерную ленту, но вы можете легко забыть делать это каждый раз, когда делаете покупки.
Знание кубических метража может помочь вам в принятии решения о покупке определенных объектов.Чтобы избежать возможных заблуждений, таких как покупка стиральной машины или холодильника, который смотрел в магазине, что он идеально впишется в ваш дом, вы должны знать перед покупкой кубические метры доступного пространства, которое у вас есть в вашем доме. Если случится так, что никто не спросит спецификации продукта, который вы собираетесь купить, вы всегда можете взять с собой мерную ленту, но вы можете легко забыть делать это каждый раз, когда делаете покупки.
Калькулятор кубических футов
С помощью нашего онлайн-приложения CalcMonster вы можете в любое время проводить измерения в кубических футах в любом количестве.Поскольку мы живем в технологическую эпоху, и теперь у всех есть смартфоны или планшеты, гораздо проще использовать приложение, которое будет очень быстро измерять кубические метры любого трехмерного пространства. Вы можете почувствовать облегчение. Вам не нужно преобразовывать разные единицы измерения, чтобы рассчитать кубический размер чего-либо, или тратить свободное время на попытки разделить на части трехмерное пространство неправильной формы. Наш калькулятор кубометров поможет вам в любое время:
Вам не нужно преобразовывать разные единицы измерения, чтобы рассчитать кубический размер чего-либо, или тратить свободное время на попытки разделить на части трехмерное пространство неправильной формы. Наш калькулятор кубометров поможет вам в любое время:
Что это такое и как рассчитать — Smart Air
Воздухообмен в час (ACH) — важный показатель для обеспечения хорошего качества воздуха и надлежащей вентиляции в помещении.Но что такое воздухообмен в час и как его рассчитать?
Что такое изменение воздуха в час?
Воздухообмен в час — это просто количество раз, когда весь воздух в комнате заменяется совершенно новым воздухом за один час. Значение «5» воздухообменов в час означает, что весь объем воздуха в комнате заменяется новым воздухом 5 раз за один час.
Очистители воздуха Очистители не заменяют воздух в помещении «новым» воздухом. Вместо этого они очищают воздух уже в комнате. Вот почему термин «e-ACH» или «эквивалентный воздухообмен в час» иногда используется для очистителей воздуха. Для очистителя воздуха, чем больше воздуха он очищает, тем выше его показатель e-ACH. Например, очиститель воздуха с 3 ACH для данного помещения будет очищать объем воздуха в помещении 3 раза в час.
Для очистителя воздуха, чем больше воздуха он очищает, тем выше его показатель e-ACH. Например, очиститель воздуха с 3 ACH для данного помещения будет очищать объем воздуха в помещении 3 раза в час.
Подробнее: ASHRAE рекомендует менять воздух в час для офисов, школ, жилых домов и т. Д.
Как рассчитать изменения воздуха в час?
Чтобы рассчитать воздухообмен в час для данного очистителя воздуха в помещении, все, что вам нужно, это два числа: 1) CADR очистителя воздуха 2) общий объем помещения.
Шаг 1. Найдите CADR
для своего очистителя воздуха
CADR измеряет количество «чистого» воздуха, выходящего из вашего очистителя воздуха. Скорость указывается либо в кубических футах в минуту (CFM), либо в кубических метрах в час (м 3 / ч). Вот пример рейтинга CADR очистителя воздуха:
.
Шаг 2: Измерьте объем вашей комнаты
Затем измерьте площадь вашего пола в квадратных футах или квадратных метрах. Затем умножьте это число на высоту вашей комнаты (в футах или метрах), чтобы получить общий объем вашей комнаты.
Шаг 3: Рассчитайте количество воздуха, заменяемого очистителем за час с помощью CADR
Если значение CADR выражено в кубических футах в минуту, необходимо умножить рейтинг CADR очистителя воздуха на 60, чтобы получить его в часах. Например, если CADR составляет 300 кубических футов в минуту, очиститель воздуха изменяет 300 * 60 = 18000 кубических футов воздуха в час. Если значение CADR указано в кубических метрах в час (м 3 / ч), то ваше число не изменится.
Шаг 4: Расчет воздухообмена в час (ACH)
Последний шаг! Возьмите число из шага 3 (воздухообмен за час очистителем) и разделите его на объем вашей комнаты из шага 2.
Воздухообмен в час (ACH) и калькулятор CADR
Для вашего удобства Smart Air создал калькулятор, который поможет вам в расчетах ACH и CADR. Просто введите два поля, и калькулятор сделает всю работу за вас! Калькулятор принимает в качестве параметров ввода и футы, и метры.
Smart Air Air Changes Per Hour (ACH) и калькулятор CADR
Пример: расчет ACH для мини-очистителя воздуха Smart Air Blast
Давайте рассмотрим пример с Smart Air Blast Mini. Blast Mini имеет скорость CADR 585 м 3 / ч, что довольно много для очистителя воздуха. Давайте посчитаем, что воздухоочиститель меняет воздух в час для комнаты площадью 50 квадратных метров (538 квадратных футов) с потолками 9 футов.
Blast Mini имеет скорость CADR 585 м 3 / ч, что довольно много для очистителя воздуха. Давайте посчитаем, что воздухоочиститель меняет воздух в час для комнаты площадью 50 квадратных метров (538 квадратных футов) с потолками 9 футов.
Мини-очиститель воздуха Smart Air Blast
- CADR воздухоочистителя 585 м 3 / час. Поскольку дано в м 3 / ч, мы умножаем это на 0,588, чтобы получить 344 кубических футов в минуту.
- Объем нашей комнаты — это наша площадь (538 квадратных футов), умноженная на высоту потолка (9 футов) = 4842 кубических фута.
- Рассчитайте воздух, перемещаемый очистителем воздуха за час, умножив наши CADR в минуту (344 кубических футов в минуту) на 60, чтобы получить 20640 кубических футов в час.
- Разделите число на шаге 3 на объем помещения (20640/4842), чтобы получить 4,26 воздухообмена в час (ACH).
Как я защищаю себя
Smart Air — это сертифицированная корпорация B, которая борется с мифами, которые используют крупные компании для завышения цен на чистый воздух.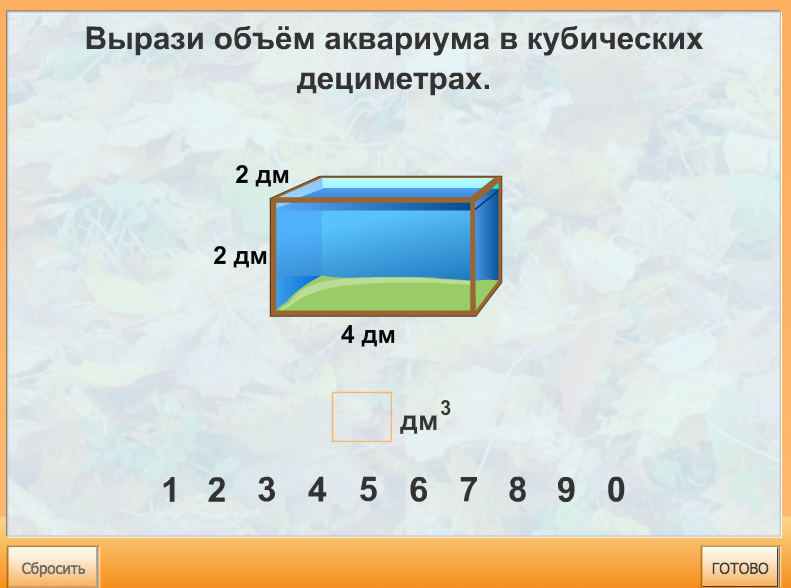
Smart Air предлагает надежные очистители и маски, подтвержденные эмпирическим путем, которые удаляют те же частицы, что и крупные компании, за небольшую часть стоимости.Только корпорации выигрывают, когда чистый воздух — роскошь.
Посмотрите на площадь!
Получите бесплатное руководство по безопасному дыханию
Присоединяйтесь к тысячам людей, чтобы быть в курсе последних исследований и знаний о том, как безопасно дышать. Зарегистрируйтесь сейчас и получите бесплатное руководство по безопасному дыханию!
Общие сведения о чистых помещениях и подсчете частиц
Общие сведения о чистых помещениях и подсчете частиц
На базовом уровне сущность чистого помещения легко понять, хотя для понимания официального определения требуется немного больше пояснений. Даже тот, кто не работает в этой сфере, может догадаться по названию, что это помещение, в котором соблюдены высокие стандарты контроля и чистоты. В качестве введения в подробности, связанные с чистым помещением, мы рассмотрим такие вещи, как контроль температуры, фильтрация, количество частиц, влажность и другие естественные переменные, а также уровни этих переменных, которые удовлетворяют нормативным требованиям.
Даже тот, кто не работает в этой сфере, может догадаться по названию, что это помещение, в котором соблюдены высокие стандарты контроля и чистоты. В качестве введения в подробности, связанные с чистым помещением, мы рассмотрим такие вещи, как контроль температуры, фильтрация, количество частиц, влажность и другие естественные переменные, а также уровни этих переменных, которые удовлетворяют нормативным требованиям.
Понимание природы чистого помещения
Загрязнение из внешней среды — одна из самых важных вещей, которую необходимо учитывать в чистом помещении, независимо от того, какие работы выполняются внутри помещения.При этом характер работы, выполняемой внутри, определяет степень важности контроля за частицами, а также классификацию, которая в конечном итоге присваивается объекту. В первую очередь следующие цифры характеризуют состояние чистого помещения при полном отсутствии каких-либо внешних загрязнений. Эти биологические элементы могут значительно изменить количество частиц; Фактически, именно эта чувствительность делает комбинезон и другое оборудование для чистых помещений важными аспектами рабочей среды — чтобы гарантировать, что внешние факторы не влияют (или вносят незначительный вклад) в подсчет частиц.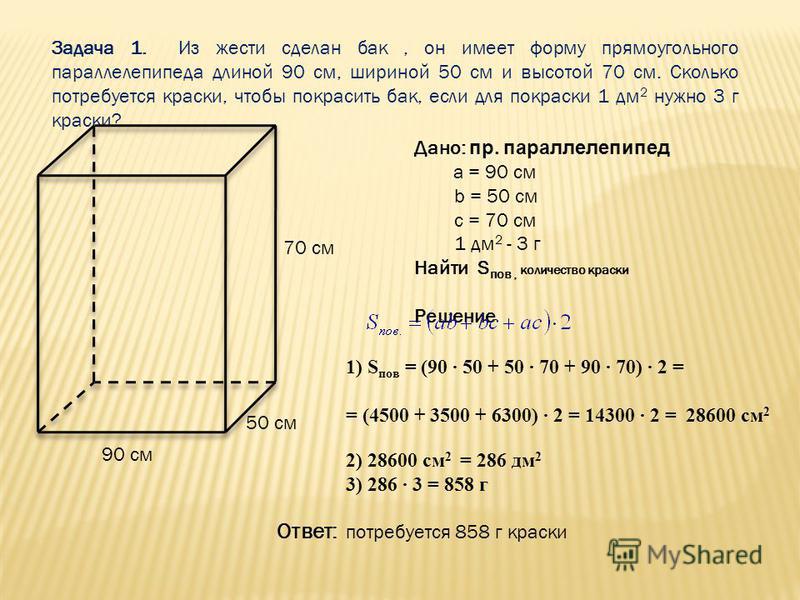
Очистка системы классификации чистых помещений
Система суждения началась как Федеральная классификация; во многих случаях с тех пор его заменила Международная организация по стандартизации. Документ, который охватывает это, называется «Чистые помещения и связанные с ними контролируемые среды — Часть 1: Сертификация чистоты воздуха » или ISO 14644-1 для содержания взвешенных в воздухе твердых частиц. Классы варьируются от 1 до 100 000, причем класс 1 является самым чистым объектом (наиболее лишенным частиц определенного размера; i.д, «лучшее» чистое помещение). Для справки, примите во внимание, что объект класса 1 ISO содержит 10 частиц размером 0,1 микрометра на кубический метр воздуха и также называется объектом класса 10 для определения этого количества частиц (это часто вызывает путаницу). Хотя в этом же объеме воздуха часто бывают частицы большего размера, они игнорируются при классификации, поскольку таких частиц значительно меньше. Эквивалент ISO находится в диапазоне от ISO класса 1 до ISO класса 9, где (класс) соответствует количеству частиц на кубический фут воздуха.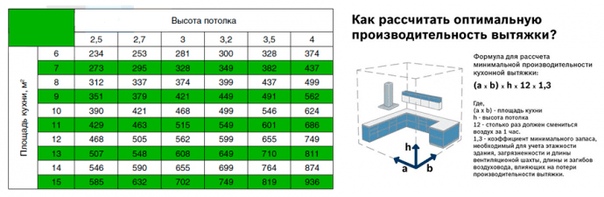 Их отношения следующие:
Их отношения следующие:
- ISO Class 1 (Class 10) — относится к чистому помещению, содержащему менее 10 частиц размером 0,1 микрометра на кубический метр воздуха. Этот же объем ограничен максимум 2 частицами размером 0,2 микрометра.
- ISO Class 2 (Class 100) — относится к чистым помещениям, которые содержат менее 100 частиц размером 0,1 микрометра на кубический метр воздуха и менее 24 частиц размером 0,2 микрометра в том же объеме.
- ISO Class 3 (Class 1000) — относится к объекту с менее чем 1000 0.Частицы размером 1 микрометр на кубический метр воздуха и максимум 237 частиц диаметром 0,2 микрометра.
- ISO Class 4 (Class 10,000) — относится к чистому помещению с менее чем 10 000 частиц размером 0,1 микрометра на кубический метр и 2 370 частицами размером 0,2 микрометра в том же объеме.
- ISO Class 5 (Class 100,000) — обозначает объект, содержащий не более 100 000 частиц размером 0,1 микрометра в каждом кубическом метре воздуха и 23 700 частиц размером 0,2 микрометра в том же объеме.

- ISO Class 6 (Class 1,000,000) — чистое помещение, содержащее до 1 миллиона частиц размером 0,1 микрометра в каждом кубическом метре воздуха и 237 тысяч частиц размером 0,2 микрометра в том же объеме.
Остальные классы ISO относятся к классу ISO 9 и основаны не на количестве частиц размером 0,1 микрометра в каждом кубическом миллиметре воздуха, а на более крупных частицах диаметром 0,5, 1 и 5 микрометров — чистые помещения обозначаются с гораздо менее строгий контроль.Как видите, есть перекрытия в измерениях. О чистом помещении судят не только по концентрации частиц, но и по размеру частиц; вы можете иметь более крупные частицы в объеме воздуха, но их должно быть меньше.
Методы контроля чистых помещений
Хотя в обозначениях чистых помещений фильтры уже установлены, они могут быть модернизированы в системе воздушного потока. Если это произойдет, обозначение класса ISO может измениться, чтобы отразить новый уровень содержания твердых частиц на кубический метр воздуха.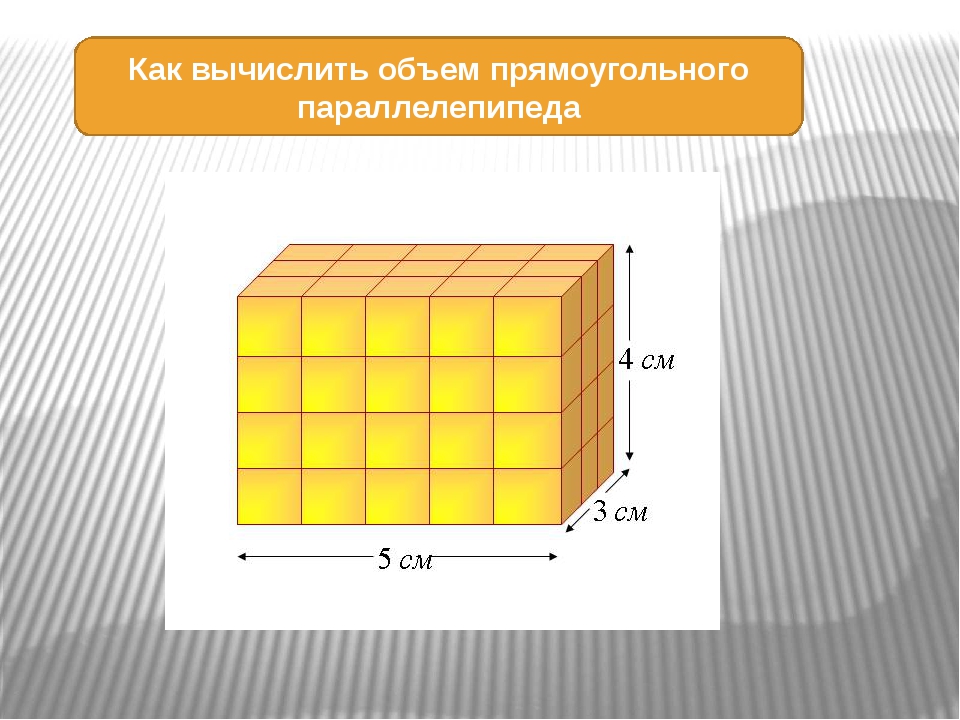 Эти высокоэффективные улавливатели твердых частиц называются HEPA-фильтрами и обладают различными конструкциями воздушного потока, которые могут продвинуть предприятие вверх по лестнице обозначений класса ISO. Еще более эффективные фильтры со сверхмалым улавливателем твердых частиц (ULPA) могут сделать чистое помещение еще чище. После того, как вы учли фильтры, следующим по важности делом в списке будет техническое обслуживание. Перчатки , лабораторные халаты , бахилы , вытяжки и другие материалы для чистых помещений составляют основную часть продаж в индустрии чистых помещений; и не зря.Их необходимо регулярно утилизировать, поскольку они собирают твердые частицы из веществ, с которыми работают внутри помещения, и увеличивают количество частиц внутри. Забота об этих вещах через определенные промежутки времени гарантирует, что ваше чистое помещение будет соответствовать обозначению ISO, а загрязнение сведено к минимуму в допустимых пределах.
Эти высокоэффективные улавливатели твердых частиц называются HEPA-фильтрами и обладают различными конструкциями воздушного потока, которые могут продвинуть предприятие вверх по лестнице обозначений класса ISO. Еще более эффективные фильтры со сверхмалым улавливателем твердых частиц (ULPA) могут сделать чистое помещение еще чище. После того, как вы учли фильтры, следующим по важности делом в списке будет техническое обслуживание. Перчатки , лабораторные халаты , бахилы , вытяжки и другие материалы для чистых помещений составляют основную часть продаж в индустрии чистых помещений; и не зря.Их необходимо регулярно утилизировать, поскольку они собирают твердые частицы из веществ, с которыми работают внутри помещения, и увеличивают количество частиц внутри. Забота об этих вещах через определенные промежутки времени гарантирует, что ваше чистое помещение будет соответствовать обозначению ISO, а загрязнение сведено к минимуму в допустимых пределах.
Как рассчитать требования к вентиляторам — гидропоника класса A
Часто задаваемые вопросы о вытяжном вентиляторе:
Обратите внимание:
Североамериканцы измеряют размер вытяжного вентилятора в CFM (кубических футах в минуту)
Европейцы измеряют размер вытяжного вентилятора в M 3 / час (кубических метров в час)
В: Как мне узнать, какой вытяжной вентилятор мне понадобится для моего помещения?
A: Чтобы узнать, какого размера вытяжной вентилятор вам понадобится, необходимо сначала рассчитать объем вашего пространства для выращивания (длина x ширина x высота), используя либо футы для измерений CFM (кубических футов в минуту), либо метры для M 3 / H (кубических метров в час) x 60 (x 60 для расчета в час только по счетчикам).
После того, как вы рассчитали объем пространства для выращивания, вы сможете увидеть точную емкость пространства для выращивания, которую необходимо обновлять в среднем один раз в минуту.
Например: Если у вас есть палатка для выращивания 1,2 м x 1,2 м x 2,0 м, вы вычислите следующее: (длина x ширина x высота) = кубические метры
1,2 x 1,2 x 2,0 = 2,88 кубических метров
2,88 x 60 = 172,8 M 3 / H (кубических метров в час)
Вентилятор с производительностью / расходом воздуха больше 172.Потребуется 8 M 3 / H .
Silenced Fan ISO-MAX 150/410 удовлетворяет потребности этого помещения для выращивания с дополнительным потоком воздуха сверх минимального требования 172,8 M 3 / H, позволяя производителю использовать этот вентилятор на более низкой скорости с 410 M 3 / H — максимальная мощность вентилятора.
Примечание: Существует множество дополнительных факторов, которые необходимо будет учитывать при расчете точной мощности вентилятора и помещения для вытяжки, например, тепло, падение эффективности фильтра, возраст оборудования и т.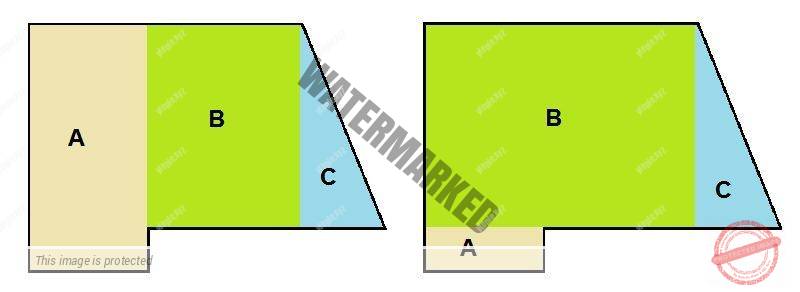 Д.Щелкните здесь, чтобы получить более подробную информацию о расчете размера вытяжного вентилятора на just4growers.com, отличном сайте для получения информации о выращивании в помещении.
Д.Щелкните здесь, чтобы получить более подробную информацию о расчете размера вытяжного вентилятора на just4growers.com, отличном сайте для получения информации о выращивании в помещении.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}} / 500
{{l10n_strings.TAGS}}
{{$ item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.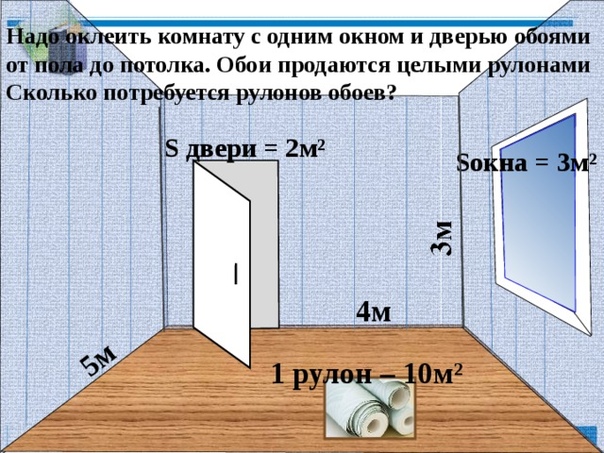 DRAG_TEXT_HELP}}
DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}}
{{$ select.selected.display}}
{{article.content_lang.display}}
{{l10n_strings.АВТОР}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}}
{{l10n_strings.
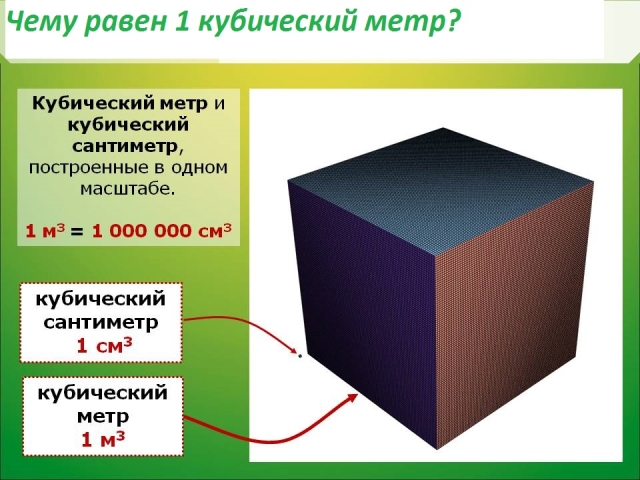

 27;
27; 1;
1;
 м.
м. м. После округления получаем 1,2 кв. м.
м. После округления получаем 1,2 кв. м.

