Передаточное число планетарного редуктора формула
Загрузить всю книгу
2.3. Передаточное отношение планетарных и дифференциальных механизмов
Звенья, вращающиеся вокруг неподвижной оси, называются основными или центральными.
Центральное колесо 1 называется солнечным, а неподвижное 3 – коронным или корончатым. Зубчатое колесо 2 имеющее подвижную ось называется сателлитом. Звено Н называется водилом или поводком. Механизмы, в состав которых входят зубчатые колеса с подвижными осями называются планетарными или дифференциальными.
Планетарными (рис. 14 а) называются механизмы, имеющие одну степень свободы. Дифференциальные (рис. 14 б) механизмы имеют две и более степени свободы.
Эти механизмы обязательно должны быть соосными, то есть оси солнечных колёс должны располагаться на одной и той же прямой линии.
Рассмотрим дифференциальный механизм (рис. 15).
где: n=4; ; .
, таким образом определённость в движении звеньев этого механизма будет в том случае, если будут известны законы движения двух его ведущих звеньев.
Так как сателлиты имеют подвижные оси, то использовать формулы для расчёта передаточного отношения механизмов с неподвижными осями не представляется возможным. В этом случае прибегают к методу инверсии (метод обращённого движения).
Будем рассматривать движение всех колёс относительно водила. Всем звеньям зададим вращательное движение с угловой скоростью водила, но в обратном направлении и найдём скорости всех звеньев механизма. Для этого вычтем угловую скорость водила из всех угловых скоростей колёс.
Скорость звена в действительном движении (до инверсии)
Скорость звена в обращённом движении (после инверсии)
Механизм, полученный в результате инверсии (остановки водила) называется обращённым (рис. 16). В результате получили обычную зубчатую передачу с неподвижными осями.
Эту зависимость (1) называют формулой Виллиса для дифференциальных механизмов.
Если бы было n – колёс, то:
где s – солнечное колесо.
Дифференциальный механизм никакого определённого передаточного отношения не имеет, если ведущим является одно из звеньев (колесо или водило), и приобретает определённость, если ведущих колёс будет два.
Передаточное отношение обращённого механизма можно рассчитать,
зная числа зубьев колёс.
У планетарных механизмов (рис. 2.29) одно из центральных (основных) колёс неподвижно, тогда формула Виллиса примет вид:
или в общем случае:
Передаточное отношение планетарного механизма от любого n-го колеса равно 1 минус передаточное отношение от этого же самого колеса к солнечному колесу, при неподвижном водиле.
Планетарными называют зубчатые передачи, содержащие зубчатые колеса с перемещающимися геометрическими осями (рис. 1, 2, 3, 4). Эти зубчатые колеса, называемые планетарными или сателлитами, движутся подобно планетам Солнечной системы, от чего и получили свое наименование. Зубчатые колеса, с которыми сцепляются сателлиты, называются центральными. Оси сателлитов закрепляются в звене передачи, называемом водилом, которое, так же как и центральное колесо, вращается вокруг центральной, или основной, геометрической оси передачи.
Рис. 1
Одно из центральных колес планетарной передачи установлено неподвижно. Ведущим (или ведомым) валом передачи служит вал подвижного центрального колеса, а ведомым (или ведущим) — вал водила. Если в планетарной передаче сделать подвижным все зубчатые колеса и водило, то такая передача называется дифференциальной или дифференциалом. В дифференциале два основных звена ведущие (или ведомые), а третье — ведомое (или ведущее).
На рис. 1 представлена схема наиболее распространенной простейшей планетарной передачи, в которой центральное колесо 1 — ведущее, водило H — ведомое, три сателлита 2 вращаются вместе с водилом вокруг центральной оси передачи, центральное колесо 3 закреплено неподвижно.
Передаточное отношение этой планетарной передачи определяют следующим образом. Допустим, что все звенья передачи (1, 2, 3 и H) жестко скреплены между собой. Сообщим этой жесткой системе переносное вращательное движение вокруг центральной оси с угловой скоростью wH, равной скорости водила wH, но обратной по знаку. При этом скорость относительного движения сцепляющихся зубчатых колес и соответственно передаточное отношение их не изменятся. При таком движении результирующая угловая скорость водила +wH+(—wH)=0, т. е. водило окажется остановленным; результирующие относительные угловые скорости зубчатых колес 1 и 3 ω1=ω1—ωH и ω′3=ω3-ωH. При ωH=0, т. е. при неподвижном водиле Я, планетарная передача превращается в простую зубчатую передачу, в которой геометрические оси всех зубчатых колес неподвижны. Для этой передачи в соответствии с формулой
передаточное отношение (сателлиты не учитываются, так как они являются паразитными колесами) i′=ω′1/ω′3=(ω1-ωH)/(ω3-ωH)
Рис. 2
Передаточное отношение i′ считается положительным при одинаковых направлениях вращения обоих зубчатых колес и отрицательным при противоположных направлениях вращения. Для рассматриваемой передачи i′ имеет отрицательное значение: i′=(ω1-ωH)/(ω3-ωH)=—(z3/z1), где z1 и z3 — соответственно числа зубьев зубчатых колес 1 и 3. Так как колесо 3 закреплено неподвижно, то ω3=0, а угловая скорость водила ωH=ω1/[1 +(z3/z1)]. Передаточное отношение данной; планетарной передачи i=ω1/ωH, или в окончательном виде
Передаточное отношение данной; планетарной передачи i=ω1/ωH, или в окончательном виде
Так же определяют передаточное отношение других видов планетарных передач.
Для двухступенчатой планетарной передачи (рис. 2), в которой каждая ступень представляет собой планетарную передачу по схеме (рис. 1) где центральное колесо 1 – ведущее, водило Н2 – ведомое, центральные колеса 3 а 4 закреплены в корпусе, передаточное отношение
Для двухступенчатой планетарной передачи (рис. 3), в которой центральное зубчатое колесо 1 – ведущее, водило H – ведомое, сателлиты 2 и 4 жестко соединены между собой и центральное колесо 3 закреплено неподвижно, передаточное отношение
Рис. 3
Для двухступенчатой планетарной передачи (рис. 4), в которой водило H – ведущее, центральное колесо 3 — ведомое, сателлиты 1 и 4 жестко соединены между собой и центральное колесо 2 закреплено неподвижно, передаточное отношение
Рис. 4
Если z1=100, z2=99, z3=100 и z4=101, то из формулы следует, что
некоторые виды планетарных передач по сравнению с простой зубчатой передачей обладают достоинством — возможностью получать большие передаточные отношения при небольшом числе зубчатых колес и небольших габаритах передачи.
Конструкции планетарных передач разнообразны. Наиболее распространены передачи, представленные на (рис. 1-3) для которых рациональные значения передаточных отношений и к. п. д. равны: по схеме (рис. 1) i=1,3. 8 и η=0,97. 0,99; по схеме (рис. 2) i=15. 60 и η=0,93..0,97; по схеме (рис. 3) i=1. 15 и η=0,97. 0,99.
3) i=1. 15 и η=0,97. 0,99.
Нагрузки со стороны каждого центрального колеса или водила воспринимаются одновременно несколькими (3. 6) сателлитами. Вследствие этого размеры зубчатых колес планетарной передачи по сравнению с простой передачей значительно меньше.
Следовательно, основные достоинства планетарных передач — большие передаточные отношения, компактность и малая масса. С помощью дифференциальных передач в машинах получается сложение или разложение движения, что используют, в частности, в автомобилях и металлорежущих станках. Однако планетарные передачи по сравнению с обыкновенными требуют повышенной точности изготовления и сложнее в сборке. Планетарные передачи благодаря своим достоинствам нашли довольно широкое применение в станкостроении, транспортном машиностроении, приборостроении.
Определение окружных сил в планетарных передачах рассмотрим на примере передачи, представленной на (рис. 1). Из рисунка следует, что
и
где T1 – крутящий момент, передаваемый шестерней 1;
dw1 — начальный диаметр этой шестерни;
а — число сателлитов;
kH=1,2. 2 — коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами. Радиальные и осевые силы определяются в зависимости от окружных сил, так же как и в простых передачах. Так как передача мощности от ведущего вала к ведомому осуществляется по нескольким потокам, число которых равно числу сателлитов, то нагрузки на зубья колес планетарных передач уменьшаются соответственно в несколько раз.
При симметричном расположении сателлитов входные и выходные валы планетарных передач нагружены только вращающим моментом и опоры этих валов разгружены от радиальных нагрузок.
Расчет на прочность зубьев колес планетарных передач производят так же, как и расчет зубьев обыкновенных зубчатых передач.
планетарная передача — планетарная шестерня — [http://slovarionline. ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы планетарная шестерня EN planetary gear … Справочник технического переводчика
ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы планетарная шестерня EN planetary gear … Справочник технического переводчика
ПЛАНЕТАРНАЯ ПЕРЕДАЧА — ПЛАНЕТАРНАЯ ПЕРЕДАЧА, зубчатая передача, имеющая колеса (сателлиты) с осями, перемещающимися вокруг центрального колеса, вращающегося вокруг неподвижной оси. Механизмы с планетарной передачей имеют малые габариты, используются в счетно решающих… … Современная энциклопедия
ПЛАНЕТАРНАЯ ПЕРЕДАЧА — зубчатая передача, имеющая колеса с перемещающимися геометрическими осями (сателлиты), которые обкатываются вокруг центрального колеса. Имеет малые габариты и массу. Используется в грузоподъемных машинах, станках, счетно решающих устройствах и т … Большой Энциклопедический словарь
Планетарная передача — ПЛАНЕТАРНАЯ ПЕРЕДАЧА, зубчатая передача, имеющая колеса (сателлиты) с осями, перемещающимися вокруг центрального колеса, вращающегося вокруг неподвижной оси. Механизмы с планетарной передачей имеют малые габариты, используются в счетно решающих… … Иллюстрированный энциклопедический словарь
Планетарная передача — Механизм для передачи вращательного движения цилиндрическими или коническими зубчатыми (реже фрикционными) колёсами, в состав которого входят т. н. Сателлиты (колёса, совершающие сложное движение и имеющие подвижную ось вращения).… … Большая советская энциклопедия
ПЛАНЕТАРНАЯ ПЕРЕДАЧА — зубчато рычажная передача, в к рой часть зубчатых колёс (сателлитов) перемещается со своими осями относительно центрального колеса вместе с водилом. П. п. применяется для передачи вращения между двумя параллельными или пересекающимися осями или… … Большой энциклопедический политехнический словарь
планетарная передача — зубчатая передача, имеющая колёса с перемещающимися геометрическими осями (сателлиты), которые обкатываются вокруг центрального колеса. Имеет малые габариты и массу. Используется в грузоподъёмных машинах, станках и т. д. * * * ПЛАНЕТАРНАЯ… … Энциклопедический словарь
Имеет малые габариты и массу. Используется в грузоподъёмных машинах, станках и т. д. * * * ПЛАНЕТАРНАЯ… … Энциклопедический словарь
Зубчатая передача — Цилиндрическая зубчатая передача Зýбчатая передача это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Назначение: передача вращательного движения между валами, которые могут иметь параллельные … Википедия
Зубчатая передача — механизм, состоящий из колёс с зубьями, которые сцепляются между собой и передают вращательное движение, обычно преобразуя угловые скорости и крутящие моменты. З. п, разделяют по взаимному расположению осей на передачи (рис. 1):… … Большая советская энциклопедия
зубчатая передача — шестерня. шестеренка. зубчатка. зубчатое зацепление. зубчатая пара. червяк. червячная передача. гипоидная передача. глобоидная передача. планетарная передача. косозубый (# шестерня). шевронный (# колесо). зуборезный (# станок). зубодолбежный.… … Идеографический словарь русского языка
Планетарные зубчатые передачи.
Планетарные зубчатые передачи
Общие сведения о планетарных передачах
Планетарными называют передачи, имеющие зубчатые колеса с подвижными осями. Отличительной особенностью механизмов, включающих планетарную передачу (или передачи), является наличие двух или более степеней свободы. При этом угловая скорость любого звена передачи определяется угловыми скоростями остальных звеньев.
Наибольшее распространение получила простая одинарная планетарная передача (рис. 1), которая состоит из центрального колеса 1 с наружными зубьями, неподвижного центрального колеса 3 с внутренними зубьями; сателлитов 2 – колес с наружными зубьями, зацепляющихся одновременно с колесами 1 и 3 (на рис. 1 число сателлитов с = 3), и водила Н, на котором закреплены оси сателлитов. Водило соединено с тихоходным валом.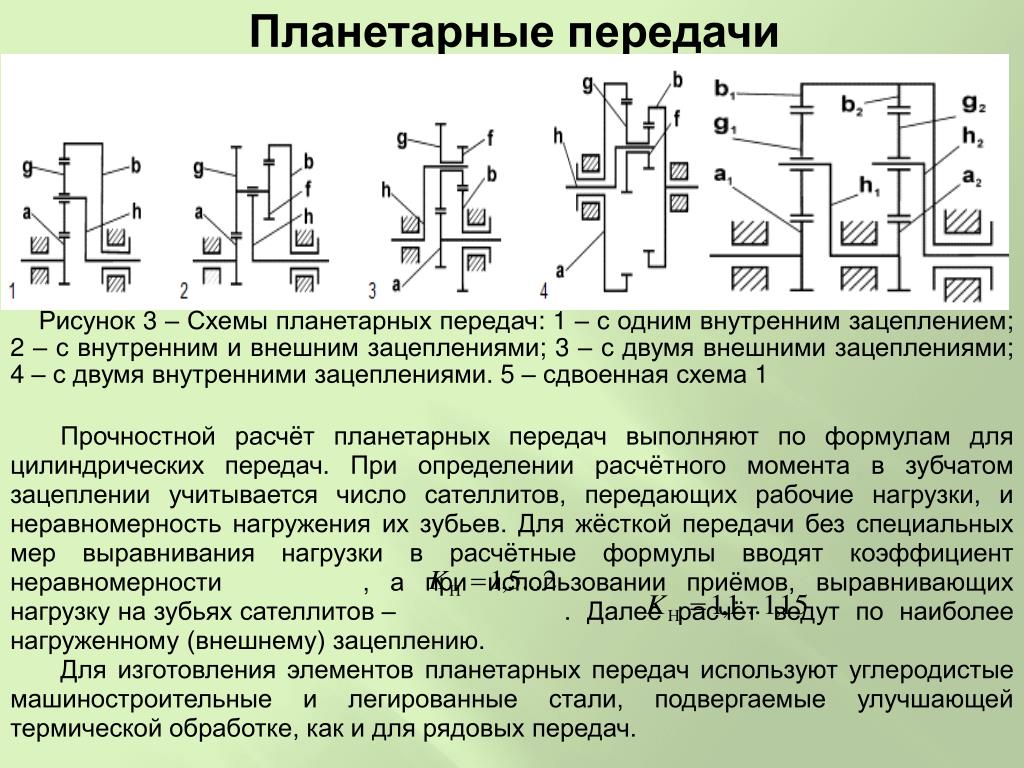 В планетарной передаче одно колесо неподвижно (соединено с корпусом). Обычно внешнее центральное колесо с внутренними зубьями называют коронным (коронная шестерня или эпицикл), а внутреннее колесо с внешними зубьями – солнечным колесом (солнечная шестерня или солнце).
В планетарной передаче одно колесо неподвижно (соединено с корпусом). Обычно внешнее центральное колесо с внутренними зубьями называют коронным (коронная шестерня или эпицикл), а внутреннее колесо с внешними зубьями – солнечным колесом (солнечная шестерня или солнце).
При неподвижном колесе 3 вращение колеса 1 вызывает вращение сателлитов 2 относительно собственных осей, а обкатывание сателлитов по колесу 3 перемещает их оси и вращает водило Н. Сателлиты таким образом совершают вращение относительно водила и вместе с водилом вокруг центральной оси, с. е. совершают движение, подобное движению планет. Поэтому такие передачи и называют планетарными.
При неподвижном колесе 3 движение передают чаще всего от колеса 1 к водилу Н, можно передавать движение от водила Н к колесу 1.
В планетарных передачах применяют не только цилиндрические, но и конические колеса с прямым или косым зубом.
Если в планетарной передаче сделать подвижными все звенья, т. е. оба колеса и водило, то такую передачу называют дифференциальной.
С помощью дифференциального механизма можно суммировать движение двух звеньев на одном или раскладывать движение одного звена на два других. Например, в дифференциале заднего моста автомобиля движение от водила Н передают одновременно колесам 1 и 3, что позволяет при повороте одному колесу вращаться быстрее другого.
***
Разновидности планетарных передач
Существует много различных типов и конструкций планетарных передач. Наиболее широко в машиностроении применяют однорядную планетарную передачу, схема которой показана на рисунке 1. Эта передача конструктивно проста, имеет малые габариты. Находит применение в силовых и вспомогательных приводах. КПД планетарной передачи η = 0,96…0,98 при передаточных числах u = 3…8.
Планетарные механизмы, в составе которых присутствуют одна или несколько планетарных передач подразделяются на однорядные, двухрядные и многорядные. Каждый набор из центральных зубчатых колёс и сателлитов, вращающихся в одной плоскости, образует так называемый планетарный ряд. Простой планетарный механизм с набором одновенцовых сателлитов является однорядным. Простые планетарные механизмы с двухвенцовыми сателлитами являются двухрядными. Сложные планетарные механизмы могут быть двух, трёх, четырёх и даже пятирядными.
Каждый набор из центральных зубчатых колёс и сателлитов, вращающихся в одной плоскости, образует так называемый планетарный ряд. Простой планетарный механизм с набором одновенцовых сателлитов является однорядным. Простые планетарные механизмы с двухвенцовыми сателлитами являются двухрядными. Сложные планетарные механизмы могут быть двух, трёх, четырёх и даже пятирядными.
Для получения больших передаточных чисел в силовых приводах применяют многоступенчатые планетарные передачи. На рис. 2,а планетарная передача составлена из двух последовательно соединенных однорядных планетарных передач. В этом случае суммарное передаточное число u = u1×u2 ≤ 64, а КПД равен η = η1×η2 = 0,92…0,96.
На рисунке 2, б показана схема планетарной передачи с двухрядным (двухвенцовым) сателлитом, для которой при передаче движения от колеса 1 к водилу Н при n4 = 0 передаточное число определяется из зависимостей:
u = n1/nН = 1 + z2z4/(z1z3).
В этой передаче u = 3…19 при КПД η = 0,95…0,97.
Как упоминалось выше, планетарные передачи, у которых все звенья подвижны, называют дифференциальными или просто дифференциалами.
Неизбежные погрешности изготовления приводят к неравномерному распределению нагрузки между сателлитами. Для выравнивания нагрузки в передачах с тремя сателлитами одно из центральных колес выполняют самоустанавливающимся в радиальном направлении (не имеющим радиальных опор). Для самоустановки сателлитов по неподвижному центральному колесу применяют сферические подшипники качения.
Высокие требования предъявляются к прочности и жесткости водила, при этом его масса должна быть минимальной. Обычно водила выполняют литыми или сварными.
***
Достоинства и недостатки планетарных передач
Основными достоинствами планетарных передач являются:
- малые габариты и масса вследствие передачи мощности по нескольким потокам, численно равным количеству сателлитов.
 При этом нагрузка в каждом зацеплении уменьшается в несколько раз;
При этом нагрузка в каждом зацеплении уменьшается в несколько раз; - удобство компоновки в машинах благодаря соосности ведущего и ведомого валов;
- работа с меньшим шумом, чем в обычных зубчатых передачах, что обусловлено меньшими размерами колес и замыканием сил в механизме. При симметричном расположении сателлитов силы в передаче взаимно уравновешиваются;
- малые нагрузки на валы и опоры, что упрощает конструкцию опор и снижает потери в них;
- возможность получения больших передаточных чисел при небольшом числе зубчатых колес и малых габаритах передачи.
Не лишены планетарные передачи и недостатков:
- повышенные требования к точности изготовления и монтажа передачи;
- большее количество деталей, в т. ч. подшипников, и более сложная сборка.
***
Область применения планетарных передач
Планетарные передачи применяют как редукторы в силовых передачах и приборах, в коробках передач автомобилей и другой самоходной техники, при этом передаточное число такой КПП может изменяться путем поочередного торможения различных звеньев (например, водила или одного из колес), в дифференциалах автомобилей, тракторов и т. п.
Широкое применение планетарные передачи нашли в автоматических коробках передач автомобилей благодаря удобству управления передаточными числами (переключением передач) и компактности. Можно встретить планетарные передачи и в механизмах привода ведущих колес современных велосипедов.
Часто применяют планетарную передачу, совмещенную с электродвигателем (мотор-редуктор, мотор-колесо).
***
Передаточное число планетарных передач
При определение передаточного числа планетарной передачи используют метод остановки водила (метод Виллиса).
По этому методу всей планетарной передаче мысленно сообщается дополнительное вращение с частотой вращения водила nН, но в обратном направлении. При этом водило как бы останавливается, а закрепленное колесо освобождается. Получается так называемый обращенный механизм, представляющий собой обычную непланетарную передачу, в которой геометрические оси всех колес неподвижны. Сателлиты при этом становятся промежуточными (паразитными) колесами, т. е. колесами, не влияющими на передаточное число всего механизма.
При этом водило как бы останавливается, а закрепленное колесо освобождается. Получается так называемый обращенный механизм, представляющий собой обычную непланетарную передачу, в которой геометрические оси всех колес неподвижны. Сателлиты при этом становятся промежуточными (паразитными) колесами, т. е. колесами, не влияющими на передаточное число всего механизма.
Передаточное число в обращенном механизме определяется как в духступенчатой передаче с одним внешним и вторым внутренним зацеплением.
Здесь существенное значение имеет знак передаточного числа. Передаточное число считают положительным, если в обращенном механизме ведущее и ведомое звенья вращаются в одну сторону, и отрицательным, если в разные стороны. Так, для обращенного механизма передачи по рис. 1 имеем:
u = u1×u2 = (-n1/n2)×(-n2/-n3) = (-z2/z1)×(z3/z2) = — z3/z1,
где z – числа зубьев колес.
В рассматриваемом обращенном механизме знак минус показывает, что колеса 2 и 3 вращаются в обратную сторону по отношению к колесу 1.
В качестве примера определим передаточное число для планетарной передачи, изображенной на рис. 1, при передаче движения от колеса 1 к водилу Н. Мысленная остановка водила в этой передаче равноценна вычитанию его частоты nН из частоты вращения колес.
Тогда для обращенного механизма этой передачи имеем:
u’ = (n1 – n2)/(n3 – nН) = — z3/z1,
где (n1 – nН) и (n3 – nН) – частоты вращения колес 1 и 3 относительно водила Н;
z1 и z3 – числа зубьев колес 1 и 3.
Для планетарной передачи, у которой колесо 3 закреплено в корпусе неподвижно (n3 = 0), колесо 1 является ведущим, а водило Н – ведомым.
Тогда получим передаточное число такой передачи:
(n1 – nН)/(- nН) = — z3/z1;
— n1/nН+ 1 = -z3/z1
или
u = n1/nН= 1 + z3/z1.
***
Подбор чисел зубьев планетарных передач
В отличие от обычных зубчатых передач расчет планетарных начинают с подбора чисел зубьев на колесах и сателлитах.
Рассмотрим последовательность подбора чисел зубьев на примере планетарной передачи, изображенной на рис. 1.
Число зубьев z1 центральной шестерни 1 задают из условия неподрезания ножки зуба: z1 ≥ 17. Принимают z1 = 24 при Н ≤ 350 НВ; z1 = 21 при Н ≤ 52 HRC и z1 = 17 при Н > 52 HRC.
Число зубьев неподвижного центрального колеса 3 определяют по заданному передаточному числу u:
z3 = z1(u – 1).
Число зубьев z2 сателлита 2 вычисляют из условия соосности, в соответствии которым межосевые расстояния aw зубчатых пар с внешним и внутренним зацеплением должны быть равны.
Из рис. 1 для немодифицированной прямозубой передачи:
aw = 0,5(d1 + d2) = 0,5(d3 – d2), (1)
где d = mz — делительные диаметры колес.
Так как модули зацеплений планетарной передачи одинаковые, то формула (1) принимает вид:
z2 = 0,5(z3 – z1).
Полученные числа зубьев z1, z2, и z3 проверяют по условиям сборки и соседства.
Условие сборки требует, чтобы во всех зацеплениях центральных колес с сателлитами имело место совпадение зубьев со впадинами, в противном случае собрать передачу будет невозможно. Установлено, что при симметричном расположении сателлитов условие сборки удовлетворяется, когда сумма зубьев центральных колес (z1 + z3) кратна числу сателлитов с = 2…6 (обычно с = 3), т. е. должно соблюдаться условие:
Установлено, что при симметричном расположении сателлитов условие сборки удовлетворяется, когда сумма зубьев центральных колес (z1 + z3) кратна числу сателлитов с = 2…6 (обычно с = 3), т. е. должно соблюдаться условие:
(z1 + z3)/c = целое число.
Условие соседства требует, чтобы сателлиты не задевали зубьями друг друга. Для этого необходимо, чтобы сумма радиусов вершин зубьев соседних сателлитов, равная da2 = m(z2 + 2) , была меньше расстояния l между их осями (рис. 1), т. е.:
da2 < l = 2aw sin (180˚/c), (2)
где aw = 0,5m(z1 + z2) – межосевое расстояние.
Из формулы (2) следует, что условие соседства удовлетворяется, когда
z2 + 2 (z1 + z2) sin (180˚/c). (3)
***
Расчет на прочность планетарных передач
Расчет на прочность зубчатых передач планетарного типа ведут по методике, применяемой для обычных зубчатых передач. Основными критериями работоспособности для большинства планетарных передач (как и для всех зубчатых передач), является усталостная контактная прочность рабочих поверхностей зубьев и прочность зубьев при изгибе. При этом под контактной прочностью понимают способность контактирующих поверхностей зубьев обеспечить требуемую безопасность против прогрессирующего усталостного выкрашивания, а прочностью при изгибе – способность зубьев обеспечить требуемую безопасность против усталостного излома зуба.
Расчет выполняют для каждого зацепления. Например, в передаче, изображенной на рис. 1, необходимо рассчитать внешнее зацепление колес 1 и 2 и внутреннее – колес 2 и 3. Так как модули и силы в этих зацеплениях одинаковы, а внутреннее зацепление по своим свойствам прочнее внешнего, то при одинаковых материалах колес достаточно рассчитать только внешнее зацепление.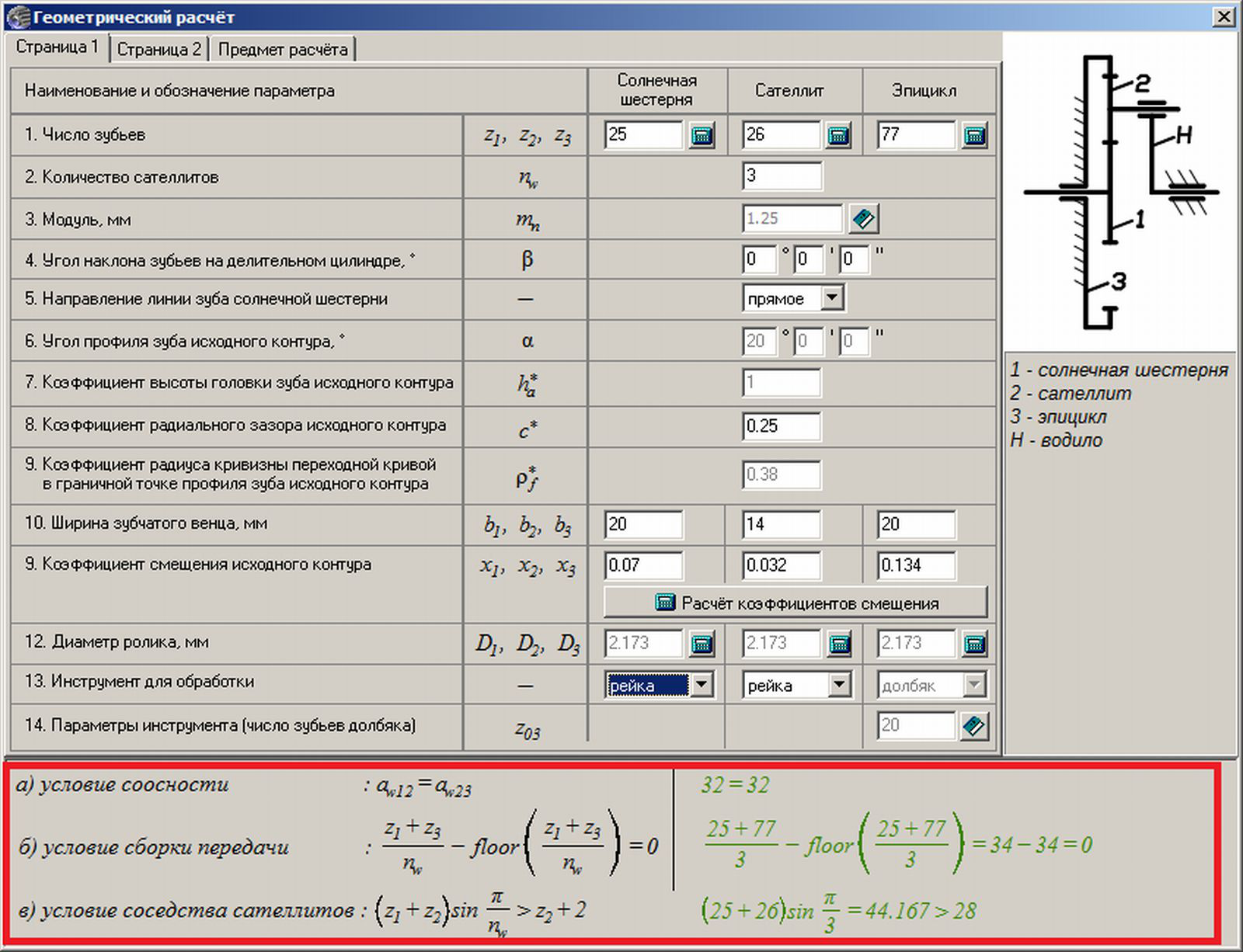
Расчет начинают с подбора чисел зубьев колес, как было показано выше.
При определении допускаемых напряжений коэффициенты долговечности находят по эквивалентных числам циклов нагружения. При этом число циклов перемены напряжений зубьев за весь срок службы вычисляют при вращении колес только относительно друг друга.
При определении допускаемых напряжений изгиба для зубьев сателлита вводят коэффициент YA, учитывающий двустороннее приложение нагрузки (симметричный цикл нагружения).
Межосевое расстояние планетарной прямозубой передачи для пары колес внешнего зацепления (центральной шестерни с сателлитом) определяют по формуле:
aw = 450(u’ + 1)× 3√{(КНТ1Кc)/(ψbau'[σ]Н2с)},
где u’ = z2/z1 – передаточное число рассчитываемой пары колес;
Кc = 1,05…1,15 – коэффициент неравномерности распределения нагрузки между сателлитами;
Т1 – вращающий момент на валу центральной шестерни, Нм;
с – число сателлитов;
ψba — коэффициент ширины венца колеса:
ψba = 0,4 для Н ≤ 350 НВ;
ψba = 0,315 при 350 НВ < Н ≤ 50 HRC,
ψba = 0,25 для Н > 50 HRC.
Ширина b3 центрального колеса 3 определяется по формуле b3 = ψbaaw.
Ширину b2 венца сателлита принимают на 2…4 мм больше значения b3; ширина центральной шестерни b1 = 1,1b2.
Модуль зацепления определяют по формуле:
m = 2aw/(z2 + z1).
Получнный расчетом модуль округляют до ближайшего стандартного значения, а затем уточняют межосевое расстояние:
aw = m(z2 + z1)/2.
Окружную силу Ft в зацеплении вычисляют по формуле:
Ft = 2×103КcТ1/сd1.
Радиальную силу Fr определяют по формуле:
Fr = Ft tg αw,
где αw = 20˚ – угол зацепления.
***
Волновые передачи
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
Передаточное число: расчет, формула, определение
Любое подвижное соединение, передающее усилие и меняющее направление движения, имеет свои технические характеристики. Основным критерием, определяющим изменение угловой скорости и направления движения, является передаточное число. С ним неразрывно связано изменение силы – передаточное отношение. Оно вычисляется для каждой передачи: ременной, цепной, зубчатой при проектировании механизмов и машин.
Перед тем как узнать передаточное число, надо посчитать количество зубьев на шестернях. Затем разделить их количество на ведомом колесе на аналогичный показатель ведущей шестерни. Число больше 1 означает повышающую передачу, увеличивающую количество оборотов, скорость. Если меньше 1, то передача понижающая, увеличивающая мощность, силу воздействия.
Общее определение
Наглядный пример изменения числа оборотов проще всего наблюдать на простом велосипеде. Человек медленно крутит педали. Колесо вращается значительно быстрее. Изменение количества оборотов происходит за счет 2 звездочек, соединенных в цепь. Когда большая, вращающаяся вместе с педалями, делает один оборот, маленькая, стоящая на задней ступице, прокручивается несколько раз.
Передачи с крутящим моментом
В механизмах используют несколько видов передач, изменяющих крутящий момент. Они имеют свои особенности, положительные качества и недостатки.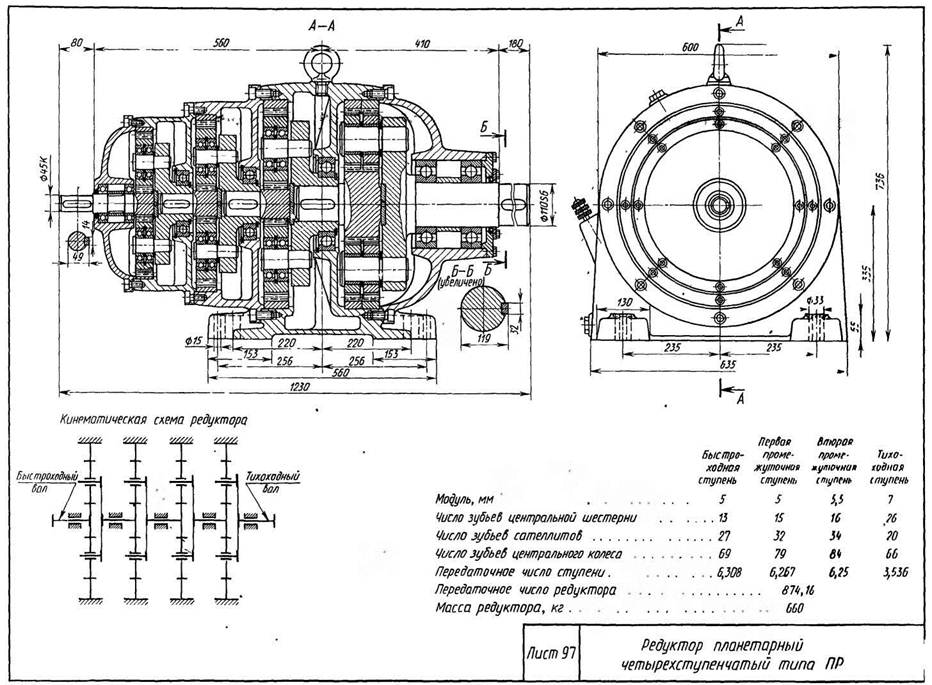 Наиболее распространенные передачи:
Наиболее распространенные передачи:
- ременная;
- цепная;
- зубчатая.
Ременная передача самая простая в исполнении. Используется при создании самодельных станков, в станочном оборудование для изменения скорости вращения рабочего узла, в автомобилях.
Ремень натягивается между 2 шкивами и передает вращение от ведущего в ведомому. Производительность низкая, поскольку ремень скользит по гладкой поверхности. Благодаря этому, ременной узел является самым безопасным способом передавать вращение. При перегрузке происходит проскальзывание ремня, и остановка ведомого вала.
Передаваемое количество оборотов зависит от диаметра шкивов и коэффициента сцепления. Направление вращения не меняется.
Переходной конструкцией является ременная зубчатая передача.
На ремне имеются выступы, на шестерне зубчики. Такой тип ремня расположен под капотом автомобиля и связывает звездочки на осях коленвала и карбюратора. При перегрузе ремень рвется, так как это самая дешевая деталь узла.
Цепная состоит из звездочек и цепи с роликами. Передающееся число оборотов, усилие и направление вращения не меняются. Цепные передачи широко применяются в транспортных механизмах, на конвейерах.
Характеристика зубчатой передачи
В зубчатой передаче ведущая и ведомая детали взаимодействуют непосредственно, за счет зацепления зубьев. Основное правило работы такого узла – модули должны быть одинаковыми. В противном случае механизм заклинит. Отсюда следует, что диаметры увеличиваются в прямой зависимости от количества зубьев. Одни значения можно в расчетах заменить другими.
Модуль – размер между одинаковыми точками двух соседних зубьев.
Например, между осями или точками на эвольвенте по средней линии Размер модуля состоит из ширины зуба и промежутка между ними. Измерять модуль лучше в точке пересечения линии основания и оси зубца. Чем меньше радиус, тем сильнее искажается промежуток между зубьями по наружному диаметру, он увеличивается к вершине от номинального размера. Идеальные формы эвольвенты практически могут быть только на рейке. Теоретически на колесе с максимально бесконечным радиусом.
Идеальные формы эвольвенты практически могут быть только на рейке. Теоретически на колесе с максимально бесконечным радиусом.
Деталь с меньшим количеством зубьев называют шестерней. Обычно она ведущая, передает крутящий момент от двигателя.
Зубчатое колесо имеет больший диаметр и в паре ведомое. Оно соединено с рабочим узлом. Например, передает вращение с необходимой скоростью на колеса автомобиля, шпиндель станка.
Обычно посредством зубчатой передачи уменьшается количество оборотов и увеличивается мощность. Если в паре деталь, имеющая больший диаметр, ведущая, на выходе шестерня имеет большее количество оборотов, вращается быстрее, но мощность механизма падает. Такие передачи называют понижающими.
Зачем нужна паразитка
При взаимодействии шестерни и колеса происходит изменение сразу нескольких величин:
- количества оборотов;
- мощности;
- направление вращения.
Только в планетарных узлах с нарезкой зубьев по внутреннему диаметру венца сохраняется направление вращения. При наружном зацеплении ставится две одинаковые шестерни подряд. Их взаимодействие не меняет ничего, кроме направления движения. В этом случае обе зубчатые детали называются шестернями, колеса нет. Вторая, промежуточная, получила название «паразитка», поскольку в вычислениях не участвует, меняет только знак.
Виды зубчатых соединений
Зубчатое зацепление может иметь различную форму зуба на деталях. Это зависит от исходной нагрузки и расположения осей сопрягаемых деталей. Различают виды зубчатых подвижных соединений:
- прямозубая;
- косозубая;
- шевронная;
- коническая;
- винтовая;
- червячная.
Самое распространенное и простое в исполнении прямозубое зацепление. Наружная поверхность зуба цилиндрическая. Расположение осей шестерни и колеса параллельное. Зуб расположен под прямым углом к торцу детали.
Когда нет возможности увеличить ширину колеса, а надо передать большое усилие, зуб нарезают под углом и за счет этого увеличивают площадь соприкосновения. Расчет передаточного числа при этом не изменяется. Узел становится более компактным и мощным.
Расчет передаточного числа при этом не изменяется. Узел становится более компактным и мощным.
Недостаток косозубых зацеплений в дополнительной нагрузки на подшипники. Сила от давления ведущей детали действует перпендикулярно плоскости контакта. Кроме радиального, появляется осевое усилие.
Компенсировать напряжение вдоль оси и еще больше увеличить мощность позволяет шевронное соединение. Колесо и шестерня имеют 2 ряда косых зубьев, направленных в разные стороны. Передающее число рассчитывается аналогично прямозубому зацеплению по соотношению количества зубьев и диаметров. Шевронное зацепление сложное в исполнении. Оно ставится только на механизмах с очень большой нагрузкой.
В конической зубчатой передачи оси расположены под углом. Рабочий элемент нарезается по конической плоскости. Передаточное число таких пар может равняться 1, когда надо только изменить плоскость действия силы. Для увеличения мощности нарезается полукруглый зуб. Передающееся количество оборотов считается только по зубу, диаметр в основном используется при расчетах габаритов узла.
Винтовая передача имеет зуб, нарезанный под углом 45⁰. Это позволяет располагать оси рабочих элементов перпендикулярно в разных плоскостях.
У червячной передачи нет шестерни, ее заменяет червяк. Оси деталей не пересекаются. Они расположены перпендикулярно в пространстве, но разных плоскостях. Передаточное число пары определяется количеством заходов резьбы на червяке.
Кроме перечисленных производят и другие виды передач, но они встречаются крайне редко и к стандартным не относятся.
Многоступенчатые редукторы
Как подобрать нужное передаточное число. Двигатель обычно выдает несколько тысяч оборотов в минуту. На выходе – колесах автомобиля и шпинделе станка, такая скорость вращения приведет к аварии. Мощности исполняющего механизма не хватит, чтобы рабочий инструмент мог резать металл, а колеса сдвинули автомобиль. Одна пара зубчатого зацепления не сможет обеспечить требуемое понижение или ведомая деталь должна иметь огромные размеры.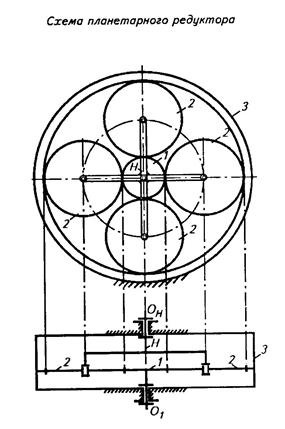
Создается многоступенчатый узел с несколькими парами зацеплений. Передаточное число редуктора считается как произведение чисел каждой пары.
Uр = U1×U2 × … ×Un;
Где:
Uр – передаточное число редуктора;
U1,2,n – каждой из пар.
Перед тем как подобрать передаточное число редуктора, надо определиться с количеством пар, направлением вращения выходного вала, и делать расчет в обратном порядке, исходя из максимально допустимых габаритов колес.
В многоступенчатом редукторе все зубчатые детали, находящиеся между ведущей шестерней на входе в редуктор и ведомым зубчатым венцом на выходном валу, называются промежуточными. Каждая отдельная пара имеет свое передающееся число, шестерню и колесо.
Редуктор и коробка скоростей
Любая коробка скоростей с зубчатым зацеплением является редуктором, но обратное утверждение неверно.
Коробка скоростей представляет собой редуктор с подвижным валом, на котором расположены шестерни разного размера. Смещаясь вдоль оси, он включает в работу то одну, то другую пару деталей. Изменение происходит за счет поочередного соединения различных шестерен и колес. Они отличаются диаметром и передающимся количеством оборотов. Это дает возможность изменять не только скорость, но и мощность.
Трансмиссия автомобиля
В машине поступательное движение поршня преобразуется во вращательное коленвала. Трансмиссия представляет собой сложный механизм с большим количеством различных узлов, взаимодействующих между собой. Ее назначение — передать вращение от двигателя на колеса и регулировка количества оборотов – скорости и мощности автомобиля.
В состав трансмиссии входит несколько редукторов. Это, прежде всего:
- коробка передач – скоростей;
- дифференциал.
Коробка передач в кинематической схеме стоит сразу за коленвалом, изменяет скорость и направление вращения.
Посредством переключения – перемещения вала, шестерни на валу соединяются поочередно с разными колесами. При включении задней скорости, через паразитку меняется направление вращения, автомобиль в результате движется назад.
При включении задней скорости, через паразитку меняется направление вращения, автомобиль в результате движется назад.
Дифференциал представляет собой конический редуктор с двумя выходными валами, расположенными в одной оси напротив друг друга. Они смотрят в разные стороны. Передаточное число редуктора – дифференциала небольшое, в пределах 2 единиц. Он меняет положение оси вращения и направление. Благодаря расположению конических зубчатых колес напротив друг друга, при зацеплении с одной шестерней они крутятся в одном направлении относительно положения оси автомобиля, и передают вращательный момент непосредственно на колеса. Дифференциал изменяет скорость и направление вращения ведомых коничек, а за ними и колес.
Как рассчитать передаточное число
Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.
Расчет без учета сопротивления
В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.
u12 = ± Z2/Z1 и u21 = ± Z1/Z2,
Где u12 – передаточное число шестерни и колеса;
Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.
Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».
В этих случаях в формуле ставится «–».
При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.
Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.
Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:
u16 = u12×u23×u45×u56 = z2/z1×z3/z2×z5/z4×z6/z5 = z3/z1×z6/z4
Способ расчета передаточного числа позволяет спроектировать редуктор с заранее заданными выходными значениями количества оборотов и теоретически найти передаточное отношение.
Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.
КПД зубчатой передачи
Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:
- трение соприкасаемых поверхностей;
- изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
- потери на шпонках и шлицах;
- трение в подшипниках.
Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.
Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.
При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.
Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.
Передаточное отношение зубчатой передачи
Значение передаточного числа зубчатой передачи совпадает передаточным отношением. Величина угловой скорости и момента силы изменяется пропорционально диаметру, и соответственно количеству зубьев, но имеет обратное значение.
Чем больше количество зубьев, тем меньше угловая скорость и сила воздействия – мощность.
При схематическом изображении величины силы и перемещения шестерню и колесо можно представить в виде рычага с опорой в точке контакта зубьев и сторонами, равными диаметрам сопрягаемых деталей. При смещении на 1 зубец их крайние точки проходят одинаковое расстояние. Но угол поворота и крутящий момент на каждой детали разный.
Например, шестерня с 10 зубьями проворачивается на 36°. Одновременно с ней деталь с 30 зубцами смещается на 12°. Угловая скорость детали с меньшим диаметром значительно больше, в 3 раза. Одновременно и путь, который проходит точка на наружном диаметре имеет обратно пропорциональное отношение. На шестерне перемещение наружного диаметра меньше. Момент силы увеличивается обратно пропорционально соотношению перемещения.
Крутящий момент увеличивается вместе с радиусом детали. Он прямо пропорционален размеру плеча воздействия – длине воображаемого рычага.
Передаточное отношение показывает, насколько изменился момент силы при передаче его через зубчатое зацепление. Цифровое значение совпадает с переданным числом оборотов.
Передаточное отношение редуктора вычисляется по формуле:
U12 = ±ω1/ω2=±n1/n2
где U12 – передаточное отношение шестерни относительно колеса;
ω1 и ω2 – угловые скорости ведущего и ведомого элемента соединения;
n1 и n2 – частота вращения.
Отношение угловых скоростей можно считать через число зубьев. При этом направление вращения не учитывается и все цифры с положительным знаком.
Зубчатая передача имеет самый высокий КПД и наименьшую защиту от перегруза – ломается элемент приложения силы, приходится делать новую дорогостоящую деталь со сложной технологией изготовления.
cccp3d.ru | Помогите с расчетом планетарно-цевочного редуктора — Page 4
Да , и еше не нравился довольно мерзкий КПД уже пр комнатной температуре, а мне надо было рассчитывать на -54 град. У меня были и есть большие сомнения, что он вообще может при такой температуре стронутся с места, ибо по-сути является редуктором скольжения.
Вы вообще о чём? Посмотрели хотя бы интернет если сами не знаете-«
Сейчас, в полной мере используя возможности современного технологического оборудования, можно реализовать ключевые преимущества которые отличают циклоидальный редуктор. А именно:
• Высокий, до 90%, коэффициент полезного действия. А, значит, малые потери на трение и нагрев;
• Возможность реализации как очень низких, так и очень высоких передаточных отношений в одной ступени; • Минимально возможное число ступеней, что влечет за собой рекордную компактность и минимальную массу;
• Малый уровень шума и малый момент инерции;
• Распределение нагрузки внутри редуктора позволяет добиться высокой износоустойчивости и способности выдерживать пятикратные перегрузки по сравнению с номинальным крутящим моментом.»
«
Основные характеристики циклоидальных редукторов
Редукторы с циклоидальным цевочным зацеплением широко распространенны по всему миру.
Использование циклоидального зацепления обеспечивает редукторам целый ряд преимуществ по сравнению с передачами с эвольвентным зацеплением:
Эффективная передача мощности.
Отсутствие в зацеплении трения скольжения обеспечивает коэффициент полезного действия одноступенчатого редуктора до 92,5% и до 85% — для двухступенчатого редуктора.
Широкий диапазон преобразования частоты вращения и компактность.
Передаточное отношение зацепления равно количеству зубьев сателлита и составляет:
— для одноступенчатого редуктора МР — от 9 до 119,
— для двухступенчатого редуктора — от 99 до 12019.
Удельная материалоёмкость редуктора 0,03-0,08 кг/Нм.
Высокая нагрузочная способность.
В планетарном редукторе с циклоидальным цевочным зацеплением в контакте с втулками цевок находятся 2/3 числа зубьев сателлита, что позволяет без поломок длительное время выдерживать большие ударные и пиковые нагрузки. Выдерживает 5-кратные пиковые перегрузки!!!
Надёжность.
Принцип работы зацепления и отработанная технология изготовления гарантируют 20000 часов непрерывной работы редуктора при постоянной нагрузке с вероятностью безотказной работы 90%. При односменной работе с постоянной нагрузкой расчетная долговечность — 15 лет.
Малая инерционность.
Все детали редуктора — тела вращения и расположены симметрично относительно общей оси редуктора. Два сателлита расположены оппозитно, что полностью уравновешивает инерционные нагрузки. Высокое передаточное число редуктора обеспечивает низкий приведенный момент инерции всего привода.
Низкий уровень шума.
Многопарность зацепления обеспечивает плавность хода, отсутствие вибраций и уровень шума в пределах 65…70 дБ.»
Кстати можно применять и эвольвентное зацепление , просто оно в этих передачах менее стойкое окажется и шестерни придётся сильно коррегировать или просто подрезать вехушки, поэтому и выбрали цевочное, но это не значит, что трение скольжения (достаточно посмотреть на КПД).
Передаточное число редуктора
Передаточное отношение: общее определение
Передаточное отношение — это соотношение угловых скоростей или крутящих моментов валов (в зависимости от строения механизма).
Передачи применяются для того, чтобы передать вращающий момент от электродвигателя к исполнительному устройству. Почему это необходимо? Дело в том, что сам мотор обычно не может передать требуемый вращающий момент, кроме того, частота вращения вала электродвигателя оказывается слишком велика, поэтому её надо понизить. Для этого и сконструированы понижающие передачи, редукторы. Таким образом удаётся изменить сразу и частоту вращения вала, и крутящий момент.
Передачи с крутящим моментом
Механизм передачи крутящего момента — редуктор — имеет входной и выходной валы.
Существует два способа передачи вращающего момента: жёсткий (момент передается жесткими звеньями, например, шестернями) и фрикционный (момент передается силами трения, работающих на поверхностях вала, например, ременная передача). Также есть возможность совмещать эти способы передачи.
Характеристика зубчатой передачи редуктора
Зубчатая передача редуктора – это механизм, состоящих из отдельных звеньев для передачи мощности через вращение зубчатых колёс. Такую зубчатую передачу используют в механических редукторах для преобразования движения.
Зубчатые редукторы очень часто задействуют в машиностроении. Именно их выбирают благодаря большому количеству преимуществ: высокому КПД, долгому сроку службы механизма, маленьким габаритам, постоянству передаточного отношения, простой и надёжной конструкции.
Также у этих редукторов есть и недостатки. К ним относят шум при больших скоростях и большие размеры редукторов, если передаточные отношения велики. Тем не менее, плюсов их использования гораздо больше, чем минусов, что и определяет итоговую востребованность.
Многоступенчатые редукторы
Как известно, современные электродвигатели выдают частоту ведущего вала примерно в районе полутора тысячи (1500) оборотов в минуту. А конечным потребителям в цепочке передачи движения обычно требуется куда меньшая частота. Стоит рассмотреть для лучшего понимания на конкретном примере. Возьмём, скажем, ленту транспортёра. Она движется медленно. Как же сделать так, чтобы надежно передать вращающий момент от электродвигателя к конечному устройству?
Здесь на помощь как раз и придут многоступенчатые редукторы. Наличие нескольких ступеней позволяет сделать компактное устройство, значительно снижающее частоту вращения вала.
Как правильно рассчитать передаточное число
Передаточное число многоступенчатого редуктора вычисляется как произведение передаточных чисел каждой ступени. Пример. В редукторе четыре зубчатые пары, передаточные отношения каждой из которых тоже равны 4. Общее передаточное число тогда будет равно 4х4х4х4 = 256.
В общем случае общее передаточное отношение редуктора равно отношению частоты вращения входного (ведущего) вала и частоты вращения ведомого (выходного) вала. Отсюда следует, что если выходной вал вращается медленнее входного, то передаточное отношение будет больше единицы. Такие передачи называют понижающими. Если же скорость выходного вала будет выше скорости входного вала, то передаточное число будет меньше единицы. В этом случае говорят о повышающей передаче или мультипликаторе.
При передаче движения всегда соответственно меняется и крутящий момент: если передача понижающая, то момент увеличивается, если повышающая, то уменьшается. Поэтому передаточное число можно представить как отношение крутящего момента на выходе к крутящему моменту на входе в редуктор.
Расчёт без учета сопротивления
Любой редуктор состоит из зубчатых пар. Чтобы рассчитать передаточное число каждой пары, надо разделить количество зубьев ведущего колеса на количество зубьев ведомого колеса.
Важно! При этом надо смотреть, меняется ли направление вращения шестеренки. Если меняется, то передаточное отношение принимается со знаком минус, если не меняется, то плюс. Направление вращения не меняется, если у колеса нарезка зубьев сделана внутри колеса.
Если в передаче участвует так называемая паразитка, то она в расчете передаточного отношения не участвует, так как ее задача лишь менять направление движения.
Также при расчете передаточных отношений можно использовать наружный диаметр шестерни. Иногда это удобно, если посчитать число зубьев затруднительно. Важно: зубчатая передача жесткая, здесь нет проскальзывания, как в ременной передаче, поэтому передаточное число всегда можно рассчитать с абсолютной точностью.
Если в редукторе применен червячный редуктор, то его передаточное отношение определяется как отношение числа зубьев ведущего колеса к числу заходов (витков) червяка. Чаще всего у червяка один заход, поэтому ясно: передаточное отношение червячной пары огромно, а вращающий момент может повышаться в десятки раз.
КПД зубчатой передачи
Преимуществами данной передачи считаются:
- Большая и неограниченная мощность.
- Небольшая масса и габариты.
- Большой коэффициент полезного действия (приблизительно 0,95-0,99).
- Надёжны, но нуждаются в большой точности изготовления.
КПД определяется как отношение реально полученной энергии к потребленной. Чем выше КПД механизма, тем больше энергии преобразовывается на полезные цели, тем меньше потери, тем эффективнее механизм.
Учёные всего мира постоянно ведут борьбу именно за сокращение непроизводительных потерь. Чтобы обеспечить хорошую работу машины с большим КПД, можно использовать масла с различными свойствами при больших изменениях температуры среды. При экспериментах с различными видами масла совместно с допустимой нагрузочной способности зубчатых передач на рабочих поверхностях зубьев не обнаружили развитие процесса разрушения, что обеспечивает отличные технико-экономические показатели машины.
Важно! КПД зубчатой передачи сильно зависит от точности изготовления зубчатых колес. В случае грубых нарушений геометрии в редукторе будут большие расходы энергии, он будет нагреваться, его КПД значительно упадёт. Поэтому редукторы следует приобретать только у проверенных производителей.
Постоянное и переменное передаточное отношение редуктора
Передаточное отношение может быть как постоянным, так и переменным. При переменном случае оно может меняться бесступенчато или ступенчато. В промышленности нашли применение обе эти схемы. Если передаточное число меняется плавно, то такое устройство называют вариатором. Эти устройства дороги и требуют точной сборки и квалифицированного обслуживания. Но всё это оправдывается конечным результатом — их полезность уже проверена временем.
Передаточное число (отношение) редуктора
Прежде всего, необходимо разобраться, что такое передаточное число редуктора. Рассмотрим на примере червячного одноступенчатого универсального редуктора Ч-100-40. В данном случае цифра 40 обозначает передаточное число (отношение) редуктора. Что это значит: при вращении быстроходного вала (входного) тихоходный вал (выходной) должен сделать один оборот вокруг своей оси за 40 оборотов входного вала.
Далее необходимо понимать различие между двумя понятиями: передаточное число фактическое и передаточное число номинальное. Номинальное передаточное число – это округленное фактическое передаточное число, это необходимо для удобства и стандартизации обозначения. Пример: редуктор Ч-100 может иметь передаточное отношение фактическое 7,75, а номинальное будет равно 8 и так далее: 10=10; 12=12,5; 15,5=16; 20=20; 24=25; 31=31,5; 40=40; 48=50; 64=63; 84=80.
Теперь рассмотрим способы определения передаточного числа редуктора, в случае если не читается бирка и отсутствует, какая либо документация на оборудование.
- Первый способ универсален для практически любого типа редуктора или редукторной части оборудования, будь то червячный, цилиндрический, конический, планетарный и так далее редуктор. Для этого необходимо покрутить быстроходный вал и количество его оборотов за один оборот тихоходного вала и будет означать фактическое передаточное число.
- Второй способ применяется в случае первого варианта и отсутствием возможности прокрутить и посчитать обороты выходного вала. Здесь существуют различия между методами определения передаточного числа червячного редуктора и, например цилиндрического:
А. Рассмотрим на примере червячного одноступенчатого универсального редуктора 1Ч-160.
Прежде всего, необходимо посчитать количество зубов червячного колеса фото № 1.
У нас получилось 32 зуба.
Затем количество заходов витка на червячном валу фото № 2.
Количество заходов 1.
Теперь 32 делим на 1 получается фактическое передаточное число редуктора 1Ч-160 равное 32.
Теперь рассмотрим способ подсчета передаточного числа червячного редуктора на примере Ч-125.
Считаем количество зубов на червячном колесе фото № 3.
У нас получается 52 зуба.
И считает количество заходов витка на червячном валу фото № 4 и № 5.
У нас получилось число равное 4.
Теперь 52 делим на 4 получается фактическое передаточное число редуктора Ч-125 равное 13.
Б.
Редукторы и способы определения их передаточного числа
В настоящее время лишь немногие современные двигатели функционируют без редуктора. Именно редукторы 5ч 100 и прочие подобные модели способствуют улучшению целого ряда характеристик при работе автомобильного двигателя.
Существует немалый список качеств, которыми характеризуются современные редукторы ч2 80 и другие распространенные модели.
Одной из наиболее весомых характеристик данных систем является их передаточное число. Определить его можно путем выявления соотношения между количеством зубцов на ведомой и ведущей шестернях.
Показатель передаточного числа, которым отличаются редукторы ч2 100, считается одним из важнейших в системе данного механизма.
Так, несколько практически идентичных согласно строению и типу конструкции редукторов могут отличаться различной степенью передаточных чисел, в результате чего становятся практически незаменяемыми друг для друга.
Решив заменить неисправный редуктор 1ц2у 100, особенно в автомобилях, которые обладают приводом на несколько мостов, желательно, для начала, определить оптимальное передаточное число устанавливаемого механизма.
Совершенно очевидно, что не стоит приобретать новый редуктор 1ц2у 125 в замену изжившей себя модели, если владелец или продавец не может подтвердить его передаточное число. Ведь в противном случае, негативные последствия применения неподходящей модели могут привести к еще большим материальным растратам.
Основные типы редукторов
Существует целый ряд параметров, которые позволят отличить редуктор 1ц2у 125 от остальных моделей и определиться с необходимыми передаточными числами.
Для этого, вначале, стоит разобраться в основных типах редукторов, которые активно применяются для обеспечения работы широкого ряда механизмов:
1) Редукторы цилиндрические двухступенчатые – отличаются одним из наиболее выгодных соотношений компактности и продуктивности функционирования. Сегодня цилиндрический двухступенчатый редуктор, нередко, можно увидеть задействованными в процессе обеспечения работы высокомощных крановых конструкций.
Благодаря своим многочисленным преимуществам цилиндрический редуктор двухступенчатый купить предпочитают специалисты в самых различных сферах деятельности.
Данные механизмы, традиционно, входят в комплектацию металлорежущих станков, сельскохозяйственных измельчителей корма для животных, приводов мешалок, прочего. Благодаря двухступенчатым редукторам способна демонстрировать продуктивную работу битумная станция дс 125 и прочие устройства.
2) Редукторы с червячным типом передачи – предназначены для обеспечения вращательных движений между перекрестными валами. Функционируют на основе червячного типа передачи и соединительного червячного колеса.
Применяются редукторы 5ч 125 и другие модели червячного типа при обеспечении работы промышленных станков, подъемных и транспортных механизмов, установок по резке металлов и общественного транспорта.
Основным достоинством, которым отличаются редукторы 1ц2у 315н и остальные распространенные модели червячного типа, является плавность хода, а также отсутствие шумов во время работы.
Среди недостатков червячных редукторов, стоит выделить повышенный уровень износоустойчивости и достаточно низкие показатели коэффициента полезного действия.
Впрочем, редукторы ч2 160 червячного типа отличаются не таким уж и высоким передаточным числом. Возможно, именно по этой причине червячные системы довольно редко отвечают современным запросам.
3) Редукторы планетарного типа – обладают сравнительно низкой удельной металлоемкостью. В то же время редукторы ч2 40 с планетарным типом строения отличаются большей способностью работы в условиях повышенных нагрузок.
4) Волновые редукторы – применяются, в основном, для обеспечения функционирования механизмов в оборонной, а также ракетно-космической промышленностях.
5) Отдельным типом редукторов являются комбинированные системы. Здесь представлены редукторы 1ц2у 400, в которых несколько типов передач соединены в едином корпусе.
Определение передаточного числа современных редукторов
Возвращаясь к теме передаточного числа редукторов, стоит отметить, что данный параметр может быть определен несколькими способами:
– По гравировке или специальной наклейке на корпусе устройства. Данный способ является наиболее простым среди всех возможных вариантов для быстрого вычисления передаточного числа, которым обладают, редукторы 1ц2у и другие подобные механизмы. В данном случае всего лишь требуется отыскать соответствующий «щиток» на корпусе устройства с информацией о необходимом параметре.
– Поиск по каталогам. Вычислить передаточное число, которым отличается редуктор 1ц2у 160 или любая другая имеющаяся модель, можно не покидая дома. Достаточно просмотреть специальный VIN номер из регистрационного свидетельства на автомобиль. Далее необходимо ввести полученные данные в поиск онлайн-каталога одного из автомобильных магазинов, после чего выбрать соответствующую трансмиссию и выяснить реальное передаточное число.
– Самостоятельный расчет. Данный способ, благодаря которому можно определить передаточное число редуктора 1ц2у 250, считается одним из самых надежных, однако неприменим в случае с автомобильными редукторами, если не планируется осуществлять разборку целого моста транспортного средства.
Как рассчитать передаточное число планетарной передачи
Обновлено 8 ноября 2020 г.
Блейк Флорной
Системы планетарных шестерен, также известные как планетарные шестерни, являются важными компонентами в современной технике. Они полезны для изменения скорости и могут быть найдены во всем: от автоматических трансмиссий автомобилей и промышленных миксеров для пищевых продуктов до операционных столов и солнечных батарей. С четырьмя основными компонентами — коронной шестерней, солнечной шестерней и планетарными шестернями, соединенными с водилом, — идея расчета передаточного числа планетарной системы может показаться устрашающей.Однако одноосный характер системы упрощает эту задачу. Только не забудьте отметить состояние водила в системе передач.
TL; DR (слишком длинный; не читал)
При расчете передаточного числа планетарной или планетарной шестерни сначала отметьте количество зубьев на солнечной и кольцевой шестернях. Сложите их вместе, чтобы вычислить количество зубьев планетарной шестерни. После этого шага передаточное число рассчитывается путем деления количества ведомых зубьев на количество ведущих зубьев — возможны три комбинации, в зависимости от того, движется ли водило, перемещается или стоит на месте.Вам может потребоваться калькулятор для определения окончательного соотношения.
Первые шаги
Чтобы максимально упростить расчет передаточного числа планетарной шестерни, запишите количество зубьев на солнечной и кольцевой шестернях. Затем сложите два числа: сумма зубьев двух шестерен равна количеству зубьев планетарных шестерен, соединенных с водилом. Например, если солнечная шестерня имеет 20 зубьев, а коронная шестерня — 60, планетарная шестерня имеет 80 зубцов. Следующие шаги зависят от состояния планетарных шестерен, подключенных к водилу, хотя все они используют одну и ту же формулу.Рассчитайте передаточное число, разделив количество зубьев ведомой шестерни на количество зубьев ведущей шестерни.
Водило как вход
Если водило действует как вход в системе планетарной шестерни, вращая коронную шестерню, пока солнечная шестерня неподвижна, разделите количество зубьев на кольцевой шестерне (ведомой шестерне) на количество зубьев планетарных шестерен (ведущих шестерен). Согласно первому примеру:
\ frac {60} {80} = 0,75
Carrier as Output
Если водило действует как выход в планетарной системе, будучи вращаемым солнечной шестерней, в то время как кольцо шестерня остается неподвижной, разделите количество зубьев планетарной шестерни (ведомой шестерни) на количество зубьев солнечной шестерни (ведущей шестерни).Согласно первому примеру:
\ frac {80} {20} = 4
Carrier Standing Still
Если водило неподвижно в планетарной системе, в то время как коронная шестерня вращает солнечную шестерню, разделите число зубьев солнечной шестерни (ведомой шестерни) на количество зубьев коронной шестерни (ведущей шестерни). Согласно первому примеру:
\ frac {20} {60} = \ frac {1} {3}
Редукторные системы | KHK Шестерни
Ссылки по теме:
Free Gear Calculator
В этом разделе представлены планетарные зубчатые передачи, гипоциклоидные механизмы и ограниченные зубчатые передачи, которые представляют собой специальные зубчатые передачи, обладающие такими характеристиками, как компактный размер и высокое передаточное число.
17.1 Планетарная зубчатая передача
Базовая форма планетарной передачи показана на рисунке 17.1. Он состоит из солнечной шестерни A, планетарной шестерни B, внутренней шестерни C и водила D.
Рис.17.1 Пример планетарной системы
Входная и выходная оси планетарной передачи находятся на одной линии. Обычно для равномерного распределения нагрузки используются две или более планетарных шестерни. Он компактен в пространстве, но сложен по конструкции. Планетарные редукторы нуждаются в высококачественном производственном процессе.Разделение нагрузки между планетарными шестернями, интерференция внутренней шестерни, баланс и вибрация вращающегося водила, опасность заклинивания и т. Д. Являются неотъемлемыми проблемами, которые необходимо решить.
Рисунок 17.1 представляет собой так называемую планетарную зубчатую передачу типа 2K-H. Солнечная шестерня, внутренняя шестерня и водило имеют общую ось.
(1) Взаимосвязь шестерен планетарной системы
Чтобы определить соотношение между количеством зубьев солнечной шестерни (za), планетарной шестерни B (zb) и внутренней шестерни C (zc) и количеством планетарных шестерен N в системе, эти параметры должны удовлетворять следующие три условия:
Условие No.1
zc = za + 2 zb (17.1)
Это условие, необходимое для совпадения межосевых расстояний шестерен. Поскольку уравнение справедливо только для стандартной зубчатой передачи, можно изменять количество зубьев, используя конструкции зубчатых колес с профильным смещением.
Для использования шестерен с профильным переключением необходимо согласовать межосевое расстояние между солнечной шестерней A и планетарной шестерней B, a1, и межосевое расстояние между планетарной шестерней B и внутренними шестернями C, α2.
α1 = α2 (17,2)
Условие No.2
Это условие необходимо для равномерной установки планетарных шестерен вокруг солнечной шестерни. Если желательно неравномерное размещение планетарных шестерен, тогда должно выполняться уравнение (17.4).
Где θ : половина угла между соседними планетарными шестернями (°)
Рис.17.2 Условия выбора передач
Условие № 3
Выполнение этого условия гарантирует, что соседние планетарные шестерни могут работать, не мешая друг другу.Это условие, которое должно быть выполнено для стандартной конструкции шестерни с одинаковым размещением планетарных шестерен. Для других условий система должна удовлетворять соотношению:
Где:
dab : Диаметр кончика планетарной шестерни
α1 : Межосевое расстояние между солнечной и планетарной шестернями
Помимо трех вышеуказанных основных условий, может существовать проблема взаимного взаимодействия между внутреннюю шестерню C и планетарную шестерню B. См. раздел 4.2 Внутренние шестерни (стр. 611–613).
(2) Передаточное число планетарной зубчатой передачи
В системе планетарной передачи передаточное число и направление вращения должны изменяться в зависимости от того, какой элемент закреплен.На рисунке 17.3 показаны три типичных типа планетарных зубчатых передач:
Рис. 17.3 Планетарный редуктор.
(а) Планетарный тип
В этом типе фиксируется внутренняя шестерня. На входе используется солнечная шестерня, а на выходе — водило D. Передаточное число рассчитывается согласно таблице 17.1.
Таблица 17.1 Уравнения передаточного числа для планетарного типа
Обратите внимание, что направление вращения входной и выходной осей одинаковое.Пример: za = 16, zb = 16, zc = 48, тогда передаточное число = 4.
(б) Тип солнечной энергии
В этом типе солнечная шестерня закреплена. Внутренняя шестерня C является входом, а ось водила D — выходом. Передаточное число рассчитывается согласно таблице 17.2.
Таблица 17.2 Уравнения передаточного числа для солнечного типа
Обратите внимание, что направления вращения входной и выходной осей одинаковы. Пример: za = 16, zb = 16, zc = 48, тогда передаточное число = 1.33333
(c) Тип звезды
Это тип, в котором фиксируется Carrier D. Планетарные шестерни B вращаются только на фиксированных осях. В строгом понимании этот поезд теряет черты планетарной системы и становится обыкновенной зубчатой передачей. Солнечная шестерня является входной осью, а внутренняя шестерня — выходной. Передаточное число:
На Рисунке 2.3 (c) планетарные шестерни являются просто холостыми.
Входная и выходная оси имеют противоположное вращение.
Пример: za = 16, zb = 16, zc = 48,
, тогда передаточное число = -3.
17.2 Гипоциклоидный механизм
При зацеплении внутренней шестерни и внешней шестерни, если разница в количестве зубьев двух шестерен довольно мала, шестерня с профильным смещением может предотвратить столкновение. Таблица 17.3 представляет собой пример того, как предотвратить столкновение в условиях z2 = 50 и разности чисел зубьев двух шестерен от 1 до 8.
Таблица 17.3 Зацепление внутренних и наружных шестерен малой разности чисел зубьев
Все вышеперечисленные комбинации не вызовут эвольвентной интерференции или трохоидной интерференции, но интерференция обрезки все же присутствует.
Для успешной сборки наружное зубчатое колесо следует собрать, вставив его в осевом направлении. Внутренняя шестерня с профильным смещением и внешняя шестерня, в которой разница в количестве зубьев мала, относятся к области гипоциклических механизмов, которые могут создавать большое передаточное число за один шаг, например 1/100.
На рисунке 17.4 зубчатая передача имеет различие в количестве зубьев всего в 1; z1 = 30 и z2 = 31. Это дает передаточное число 30.
Рис. 17.4 Зацепление внутреннего зубчатого колеса и внешнего зубчатого колеса, в котором разность чисел зубьев равна 1
17.3 Система зубчатых передач с фиксированной передачей
Планетарная зубчатая передача, имеющая четыре зубчатых колеса, является примером системы передач с ограничениями. Это замкнутая система, в которой мощность передается от ведущей шестерни через другие шестерни и, в конечном итоге, на ведомую шестерню. Система передач с замкнутым контуром не будет работать, если шестерни не соответствуют определенным условиям.
Пусть z1, z2 и z3 будут числами зубьев шестерни, как на рисунке 17.5 Создание сетки не может работать, если длина жирной лески (ремня) не делится равномерно на шаг. Уравнение (17.11) определяет это условие.
Рис. 17.5 Система с промежуточной шестерней
На рисунке 17.6 показана система передач с ограничениями, в которой зубчатая рейка находится в зацеплении. Жирная линия на рисунке 17.6 соответствует поясу на рисунке 17.5. Если длина ремня не может быть равномерно разделена по шагу, система не работает. Он описывается уравнением (17.12).
Фиг.17.6 Зубчатая передача с зубчатой рейкой
Ссылки по теме:
Прямозубые цилиндрические шестерни
Планетарный редуктор
Планетарный редуктор | KHK Шестерни
Трансмиссия и планетарный механизм
Многие «шестерни» используются для автомобилей, но они также используются для многих других машин. Наиболее типичным из них является «трансмиссия», которая передает мощность двигателя на шины. В общих чертах, трансмиссия автомобиля играет две роли: первая — замедлять высокую скорость вращения, создаваемую двигателем для передачи на шины; другой — изменить передаточное число в соответствии с ускорением / замедлением или скоростью движения автомобиля.
Скорость вращения автомобильного двигателя в общем состоянии движения составляет 1 000 — 4 000 оборотов в минуту (17 — 67 в секунду). Поскольку невозможно вращать шины с одинаковой скоростью вращения для движения, необходимо снизить скорость вращения, используя соотношение числа зубьев шестерни. Такая роль называется замедлением; соотношение скорости вращения двигателя и шин называется передаточным числом.
Тогда почему необходимо изменять передаточное число в соответствии с ускорением / замедлением или скоростью движения? Это связано с тем, что веществам требуется большая сила, чтобы начать движение, однако им не требуется такая большая сила, чтобы продолжать движение после того, как они начали движение.Автомобиль можно назвать хорошим примером. Однако двигатель по своей природе не может так точно изменять свою мощность. Следовательно, один регулирует его выход, изменяя передаточное число, используя трансмиссию.
Передача движущей силы через шестерни очень похожа на принцип рычага (рычага). Отношение числа зубьев шестерен, входящих в зацепление, можно рассматривать как отношение длины плеч рычагов. То есть, если передаточное число велико, а скорость вращения на выходе мала по сравнению с входной, выходная мощность при передаче (крутящий момент) будет большой; с другой стороны, если скорость вращения на выходе не так низка по сравнению со скоростью на входе, выходная мощность (крутящий момент) будет небольшой.Таким образом, изменение передаточного числа с использованием трансмиссии во многом похоже на принцип перемещения вещей.
Тогда как трансмиссия изменяет передаточное число? Ответ кроется в механизме, называемом планетарной зубчатой передачей.
Планетарный механизм — это зубчатый механизм, состоящий из 4 компонентов, а именно солнечной шестерни A, нескольких планетарных шестерен B, внутренней шестерни C и водила D, соединяющего планетарные шестерни, как показано на графике ниже. Он имеет очень сложную структуру, что затрудняет его проектирование или производство; он может реализовать высокое передаточное число с помощью шестерен, однако это механизм, подходящий для редукционного механизма, который требует как малых размеров, так и высоких характеристик, например, трансмиссии для автомобилей.
График 17.1: Конструкция планетарного редуктора.
Механизмы планетарной передачи обладают способностью изменять передаточное число, выбирая, какой из компонентов должен быть зафиксирован.
Например, предположим, что внутренняя шестерня C зафиксирована, входная ось соединена с солнечной шестерней A, а водило выходной оси D. Когда солнечная шестерня A вращается один раз,
планетарная шестерня B будет вращаться несколько раз.
Если внутренняя шестерня C не зафиксирована, а вместо нее фиксировано водило D, когда планетарная шестерня B вращается один раз, внутренняя шестерня C будет вращаться несколько раз.Это означает, что когда солнечная шестерня A вращается один раз, внутренняя шестерня C будет вращаться один раз.
Но поскольку на самом деле внутренняя шестерня C зафиксирована, а водило D будет находиться в движении, весь механизм планетарной шестерни следует рассматривать только во времени вращения.
Затем солнечная шестерня A повернется раз, а водило D —
раз, что приведет к уменьшению передаточного числа.
Затем предположим, что водило D зафиксировано, входная ось соединена с солнечной шестерней A, а внутренняя шестерня C выходной сателлита. В этом случае планетарная шестерня B будет вращаться только для передачи движущей силы в качестве второстепенной шестерни.Кроме того, поскольку внутренняя шестерня C будет вращаться в направлении, обратном солнечной шестерне A, передаточное число будет равным.
Таким образом, фиксируя и вращая компоненты зубчатого механизма, трансмиссия изменяет передаточное число, не требуя большого механизма.
Приложение — планетарная передача
Эта статья воспроизводится с разрешения автора.
Masao Kubota, Haguruma Nyumon, Tokyo: Ohmsha, Ltd., 1963.
Планетарная передача — это зубчатая передача, состоящая из шестерни (солнечной шестерни), которая закреплена или вращается вокруг фиксированного центра, а шестерня (планетарная шестерня) вращается вокруг центра, который вращается вокруг солнечной шестерни.На рис. 12.9 показана простейшая планетарная передача. Когда шестерня A (число зубьев α) зафиксирована (неподвижная солнечная шестерня) и рычаг C вращается в направлении ωc, а шестерня B (планетарная шестерня, число зубцов b) вращается во время вращения.
Рис 12.9 Очень простая планетарная передача
Считая угловую скорость пространства, в котором он вращается, равной ωb, получим соотношение между ωb и ωc. Во-первых, скорость v2 в центре O2 планетарной шестерни B равна ωc на O1O2.С другой стороны, точка P зафиксирована, потому что шестерня A не вращается. Поскольку шестерня B вращается вокруг точки B с угловой скоростью со скоростью ωb, v2 = ωb на PO2. Следовательно,
ωb / ωc = O1O2 / PO2 = a + b / b
(12,3)
В качестве альтернативы вы можете рассмотреть следующее: рассматривать вращение, когда шестерня A и B находится в зацеплении, в то время как рычаг C фиксируется, как нормальное зацепление, затем дать A обратное вращение, в то время как A, B и C взаимно фиксированы. Затем вращение A становится равным 0 (фиксировано), а вращение B и C показано в таблице 12.1.
Таблица 12.1
| А | B | C | ||
| Против C | 1 | — а / б | 0 | |
| С C | -1 | -1 | -1 | (+ |
| 0 | — (1 + а / б) | -1 |
Когда C вращает -1 оборот, B вращает — (a + b) / b, и это соответствует результату формулы 12.3.
Рис. 12.10 Обратно-планетарная шестерня с внешней шестерней
Рис. 12.10 показывает типичную обратную планетарную передачу, которая поворачивается назад и передает вращение от неподвижной солнечной шестерни на концентрическую вращающуюся солнечную шестерню через планетарную шестерню. Вы можете получить большое передаточное число, используя небольшую машину. Этот механизм используется для понижающей / ускоряющей передачи. На картинке выше зацепление представляет собой солнечную шестерню A -> планетарную шестерню B -> планетарную шестерню C (соединенную с шестерней B) -> солнечную шестерню D (концентрическую, но не соединенную с шестерней B) и шестерню. A фиксируется, а рычаг E вращается.
Чтобы получить передаточное число, сначала зафиксируйте рычаг E и получите вращение каждой шестерни за один оборот шестерни A, затем вычислите количество оборотов каждой шестерни, задав шестерне A -1 оборот, как в таблице 12.2.
Таблица 12.2
| А | B | C | D | E | ||
| Против E | +1 | — а / б | — а / б | ac / bd | 0 | |
| С E | -1 | –1 | -1 | –1 | -1 | (+ |
| 0 | — (1 + а / б) | — (1 + а / б) | — (1-ac / bd) | -1 |
Следовательно, если угловая скорость плеча равна ωe, угловая скорость ωd солнечной шестерни D выражается с помощью следующей формулы:
ωd = — (ac / bd — 1) ωe
(12.4)
В этом случае D обратно пропорционально E, когда ac> bd, D и E синхронно вращаются, когда ac Существуют различные формы планетарной передачи в дополнение к вышеперечисленным, например, с внутренним зацеплением, как на рис. 12.11 и в таблице 12.3, или с коническим зубчатым колесом, как на рис. 12.12. Когда какая-либо внешняя шестерня заменяется внутренней шестерней, используйте знак минус для радиуса делительной окружности в формуле для передаточного числа. Рис. 12.11 Планетарная передача с обратным ходом и внутренним зацеплением Рис. 12.12 Планетарная передача с конической шестерней Таблица 12.3 Ссылки по теме: Уравнения и калькуляторы планетарных эпициклических передаточных чисел Связанные ресурсы: шестерни Конструкция и проектирование зубчатых передач Уравнения и калькуляторы для определения передаточных чисел планетарных или планетарных шестерен в сборе Где: D = Вращение привода на оборот ведомого, ведомой шестерни или шкива.Обороты / Обороты … или множитель отношения скорости привода к ведомому. Для всех калькуляторов требуется Премиум-членство Примечание: Во всех случаях, если D известен, F = 1 / D, или, если F известен, D = 1 / F. Направление вращения. Если расчетный результат отрицательный, привод и ведомый будут вращаться в противоположных направлениях; в противном случае неотрицательный ответ означает, что оба будут вращаться в одном направлении. Рисунки 19–22 используются для получения передаточных чисел, когда два приводных элемента вращаются с разными скоростями. Это типы составных дисков. Планетарная коническая шестерня . — Две формы планетарной шестерни конического типа показаны на рисунках 23 и 24. Планетарная шестерня на рисунке 23 вращается вокруг неподвижной конической шестерни, в центре которой находится ведомый вал. На рисунке 24 показан редуктор Humpage. Это иногда называют обратным зацеплением конического шкива из-за его использования в конических шкивах некоторых типов станков. © Copyright 2000-2021, Engineers Edge, LLC www.engineersedge.com | Обратная связь | Реклама Дата / Время: Уравнение Уиллиса описывает движение отдельных шестерен планетарной коробки передач (планетарной передачи). Изменение скорости планетарных коробок передач уже не так легко понять, как изменение скорости стационарных трансмиссий.Это связано с тем, что движение вращающихся планетарных шестерен в конечном итоге представляет собой суперпозицию трех различных движений. Движение больше не состоит из простого вращения вокруг своей оси, но сама ось выполняет дополнительное круговое движение вокруг оси солнечной шестерни, в то время как планетарная шестерня также выполняет дополнительное круговое движение из-за вращения солнечной шестерни. Анимация: движение планетарной передачи Таким образом, движение вращающейся планетарной передачи можно проследить до наложения трех отдельно наблюдаемых движений: Однако движения не являются независимыми друг от друга, поскольку планетарная шестерня вращается на солнечной шестерне.Таким образом, соотношение диаметров солнечной шестерни и планетарной шестерни определяет, как часто планетарная шестерня вращается вокруг своей оси, когда она совершает один оборот вокруг солнечной шестерни. Чтобы определить соотношение скоростей вращения между солнечной шестерней, планетарной шестерней и водилом, вышеупомянутые движения сначала описываются отдельно, а затем накладываются друг на друга. Для ясности предполагается, что шестерни представляют собой (шаговые) цилиндры. Рис.: Принципиальная конструкция планетарной шестерни Если солнечная шестерня стоит на месте и планетарная шестерня надежно зафиксирована на водиле, то угол стреловидности водила φ c соответствует угловому положению планетарной шестерни φ p1 . \ begin {align} Рис.: Вращение оси планетарной шестерни вокруг солнечной шестерни Фактически, планетарная шестерня будет катиться по солнечной шестерне, когда она установлена с возможностью вращения на водило, и, таким образом, вращается вокруг своего собственного центра тяжести. Таким образом, планетарная шестерня повернется на дополнительный угол φ p2 . Если рассматривать простое движение качения, то длина дуги b c , которую водило покрыло на солнечной шестерне, точно соответствует длине дуги b p2 , на которую планетарная шестерня переместилась по своей окружности.Дополнительный угол φ p2 может быть определен в радианах следующим образом: \ begin {align} Рис.: Вращение планетарной шестерни вокруг собственного центра тяжести Теперь водило удерживается на месте, и солнечная шестерня вращается по часовой стрелке на угол φ s .В этом случае планетарная шестерня повернется против часовой стрелки на угол φ p3 . Аналогично предыдущему случаю, применяется следующее утверждение: длина дуги b s на окружности солнечной шестерни соответствует длине дуги b p3 , на которую планетарная шестерня переместилась по окружности: \ begin {align} Рис.: Вращение планетарной шестерни из-за вращения солнечной шестерни Знак «минус» означает, что планетарная шестерня движется в направлении, противоположном движению солнечной шестерни. Движения планетарной передачи в соответствии с уравнениями (\ ref {P1}), (\ ref {P2}) и (\ ref {P3}), которые до сих пор рассматривались отдельно, теперь могут быть наложены на общую движение: \ begin {align} Рисунок: Суперпозиция движений Угловые положения φ, содержащиеся в этом уравнении, являются результатом соответствующей угловой скорости ω и прошедшего времени t (φ = ω⋅t), при этом угловая скорость напрямую связана со скоростью вращения n соотношением ω = 2π Номер телефона: \ begin {align} Если уравнение (\ ref {varp}) используется в уравнении (\ ref {P}), в конечном итоге получается следующая зависимость между скоростью вращения планетарной шестерни n P и скоростью вращения солнечной шестерни n с и носитель n c : \ begin {align} Поскольку диаметр делительной окружности d шестерни прямо пропорционален количеству зубьев z, приведенное выше уравнение также может быть выражено соответствующим количеством зубьев: \ begin {align} Это уравнение называется фундаментальной формулой планетарных шестерен (также называется уравнением Уиллиса ).Уравнение Уиллиса используется для определения различных передаточных чисел в зависимости от режима работы, что будет более подробно объяснено в статье Уравнение Уиллиса для планетарных шестерен. Планетарные передачи Планетарные редукторы представляют собой высокоточные устройства управления движением, которые создают значительный крутящий момент для своего размера, обладают высокой жесткостью на кручение и низким люфтом, что делает их подходящими для широкого круга задач. — постановка задач. Планетарные редукторы Micron AquaTrue обеспечивают защиту IP67 от агрессивных чистящих химикатов и промывки под высоким давлением. Например, отдельные типы планетарных редукторов: • Работайте круглосуточно, семь дней в неделю, более 30 000 часов в картонных упаковках. Редукторы с пожизненной смазкой не требуют технического обслуживания, а высокое отношение крутящего момента к размеру обеспечивает компактные размеры корпуса и небольшую занимаемую площадь на машине. • Помогает достичь точности в пределах нескольких десятитысячных дюйма на машинах плазменной резки благодаря исключительно низкому люфту.Винтовая зубчатая передача обеспечивает быстрое позиционирование и плавное движение, а герметичные редукторы не пропускают абразивную пыль, образующуюся во время резки. • Ограничьте шум и вибрацию и соблюдайте строгие требования к люфту в столах для сканирования сердечно-сосудистых пациентов. • Позвольте пищевому оборудованию нарезать мясо, хлеб и замороженные продукты со скоростью до четырех ломтиков в секунду. Также доступны тонкие прямоугольные конструкции, которые вписываются в габариты машины и обеспечивают бесшумную и плавную работу. Планетарные основы — передаточные числа, углы винтовой линии, осевые нагрузки, коронация Планетарный редуктор принимает высокоскоростной вход с низким крутящим моментом, скажем, от электродвигателя, затем увеличивает крутящий момент и снижает скорость на выходе за счет передаточного числа редуктора. Это позволяет двигателям работать на более высоких и более эффективных оборотах в минуту в оборудовании, которое работает на низких скоростях. Это также снижает инерцию, отраженную обратно в двигатель, повышая стабильность. А использование планетарного редуктора часто позволяет машиностроителям уменьшить размер и стоимость оборудования для управления перемещением. Планетарные агрегаты с косозубыми шестернями, а не прямозубые, имеют большее передаточное отношение. Коэффициент контакта — это количество зубьев в сетке в любой момент времени. В то время как обычная прямозубая зубчатая передача имеет коэффициент контакта 1,5, косозубая зубчатая передача увеличивает его более чем вдвое до 3,3. Преимущества более высокого отношения контактов: Редуктор Micron EverTrue предназначен для непрерывного режима работы. Он может работать без остановок, не превышая 140 ° F, и работать более 30 000 часов. • На 30–50% больше крутящего момента, чем у эквивалентной цилиндрической планетарной передачи. Угол наклона винтовой линии редуктора также оказывает значительное влияние на производительность, поскольку чем больше угол, тем больше зубьев в зацеплении одновременно. Таким образом, увеличение угла наклона спирали с типичных 12 ° до 15 ° увеличивает крутящий момент на 17–20%; и на 40% по сравнению с прямозубыми цилиндрическими зубчатыми колесами. Шестерни с углом наклона спирали 15 ° также издают меньше шума. Зубья косозубой шестерни создают осевые нагрузки на вал двигателя. Подшипники редуктора должны компенсировать эти нагрузки. В цилиндрических редукторах, использующих шарикоподшипники с небольшой осевой нагрузкой или без нее, может возникнуть преждевременный выход из строя подшипников двигателя или редуктора. Лучше использовать конические роликоподшипники, например, в редукторах Micron Helical, чтобы полностью компенсировать осевые нагрузки. Диапазон передаточных чисел одноступенчатого планетарного редуктора от 3: 1 до 10: 1. Передаточное число не может превышать 10: 1, потому что ведущие шестерни могут быть очень маленькими.Передаточное число более 10: 1 возможно с дополнительной планетарной ступенью, хотя обычно это увеличивает длину и стоимость. Планетарные конструкции также не могут иметь передаточное число меньше 3: 1, потому что тогда шестерня и внешнее зубчатое колесо должны быть почти одинакового размера, не оставляя места для планетарных шестерен. Передаточные числа от 4: 1 до 8: 1 обеспечивают наилучшее сочетание размера шестерни и планетарной передачи, производительности и срока службы. Коронация включает в себя небольшое изменение профиля зубьев шестерни для улучшения соосности зубчатого зацепления, увеличения крутящего момента и снижения шума.Он также улучшает распределение нагрузки на боковую поверхность зуба, тем самым сводя к минимуму области высокого напряжения, которые могут вызвать точечную коррозию. Планетарные передачи преобразуют входные сигналы с высокой скоростью и низким крутящим моментом в выходы с низким крутящим моментом и высоким крутящим моментом. Для эффективной работы планетарного редуктора необходим некоторый зазор. Зазор предотвращает чрезмерный нагрев и износ шестерен и обеспечивает хорошую смазку. Но небольшой зазор между зубьями шестерни приводит к потере хода. Реальные редукторы также не могут иметь бесконечную жесткость на скручивание, поэтому накат (изгиб) в редукторе приводит к дополнительному потерянному движению. Понимание того, как разные производители измеряют люфт, важно при выборе редуктора. Нет строгих стандартов, регулирующих, как измерять люфт. Это может привести к путанице и неправильным представлениям. Некоторые производители измеряют и усредняют четыре или более точек на выходном валу, чтобы получить характеристику люфта. Используя этот метод, блок с измерениями люфта 4, 6, 10 и 12 угловых минут будет иметь номинальное значение 8 угловых минут. Инженеры Thomson считают, что зазор должен основываться на самом большом измерении на выходном валу, поэтому в приведенном выше примере будет получено номинальное значение 12 угловых минут. Кроме того, некоторые производители применяют 2% номинального крутящего момента для создания номинального люфта, в то время как другие применяют меньше. Последний дает более низкие измерения люфта и не дает истинных оценок люфта в течение срока службы продукта. Люфт со временем будет увеличиваться. Планетарный редуктор может иметь зазор из коробки 8 угловых минут, но, например, 15 угловых минут после шести месяцев использования. Поэтому то, насколько хорошо планетарный редуктор сохраняет точность в течение всего срока службы, является важным фактором для большинства пользователей. Размер и выбор планетарного редуктора Планетарный редуктор с цилиндрической коронкой обеспечивает плавное движение с низким люфтом, позволяя станкам плазменной резки сохранять точность в пределах нескольких десятков тысячных долей дюйма. Правильный выбор редуктора и точный размер имеют решающее значение для долгого и надежного срока службы. В качестве отправной точки разработчики могут приблизительно определить требуемый размер редуктора от: T r = T м × r × e , где T r = крутящий момент приложения, T м = постоянный крутящий момент, r = передаточное отношение и e = эффективность. Однако, чтобы точно определить размер редуктора, инженеры должны учитывать полный профиль движения, включая скорость, крутящий момент, ускорение, замедление и частоту цикла. И они должны применять понижающий коэффициент для условий с высокой циклической нагрузкой. (Типичные значения приведены в таблице.) Непрерывная работа в непрерывном режиме не требует факторов снижения номинальных характеристик. В таких случаях наиболее распространенной проблемой является перегрев, который разрушает смазку и приводит к выходу из строя шестерен. Высокопроизводительные редукторы, такие как Micron EverTrue, рассчитаны на круглосуточную работу без выходных, при температуре ниже 140 ° F и срок службы более 30 000 часов. Онлайн-инструменты для выбора и определения размеров позволяют сэкономить время, позволяя инженерам находить и сравнивать планетарные редукторы, подходящие для конкретного применения. (См. Дополнительную информацию на боковой панели.) Устранение неисправностей Планетарный редуктор Некоторые проблемы могут возникнуть в редукторах, размер и установка которых не соответствуют требованиям. Несоответствующая входная частота вращения, передаточное отношение редуктора, выходной крутящий момент, радиальные и осевые нагрузки, а также ошибки монтажа могут способствовать возникновению шума редуктора.Но правильный монтаж имеет решающее значение для минимизации шума и повышения производительности. Многие редукторы необходимо устанавливать на серводвигатель в вертикальном положении. Это позволяет валу двигателя центрировать редуктор. После установки на двигатель редуктор можно использовать в любом положении. Слишком много смазки, компоненты с недопустимыми допусками и плохое качество зубчатых колес или подшипников могут вызвать чрезмерное трение и сопротивление. Ищите производителей редукторов, которые проверяют каждый редуктор на входное сопротивление перед отгрузкой.Каждый размер и соотношение имеют допустимый диапазон сопротивления, и пиковые уровни следует измерять в обоих направлениях. Для приложений, требующих защиты от пыли, грязи и воды, имейте в виду, что сочетание двигателя со степенью защиты IP65 и редуктора со степенью защиты IP65 не всегда обеспечивает защиту IP65. Посмотрите внимательно, как герметизируется стык между двигателем и редуктором. Лучшим подходом является использование уплотнительных колец между всеми корпусами для защиты IP65 на всей сборке. Планетарный редуктор нового типа Micron AquaTrue соответствует требованиям IP67 для обработки, упаковки и раздачи продуктов питания и напитков благодаря круглому корпусу из нержавеющей стали без внешних швов. Такие редукторы могут выдерживать щелочные химические чистящие средства и промывки под высоким давлением, что дает инженерам возможность устанавливать их без дополнительных затрат и сложности компонентов, таких как кожухи, экранирование и механические передачи. Масло или консистентная смазка могут эффективно смазывать планетарные редукторы.Смазка имеет то преимущество, что она обеспечивает смазку на весь срок службы редуктора, что исключает необходимость в частом техническом обслуживании. Смазка допускает установку в любом положении и устраняет опасения по поводу утечки. Масло требует обслуживания и повторной смазки, обычно каждые несколько тысяч часов. А утечки всегда являются проблемой при смазке маслом. Ориентация при масляной смазке обычно ограничена, должна указываться при заказе и обычно не может быть изменена. Распространенное заблуждение состоит в том, что маслонаполненные агрегаты всегда работают холоднее, чем редукторы, смазываемые консистентной смазкой.На самом деле уплотнение, необходимое для маслонаполненной коробки передач, часто выделяет больше тепла, чем экономит масло. Онлайн-выбор и определение размеров — попробуйте один вариант Онлайн-инструменты для определения размеров и выбора редуктора упрощают процесс поиска редуктора, подходящего для конкретной области применения. Одним из универсальных инструментов для определения размеров является Micron Motioneering. Его Размер и выбор Режим позволяет пользователям вводить параметры приложения, такие как скорость, выходной крутящий момент, а также радиальные и осевые нагрузки, и инструмент рекомендует редукторы, которые подходят для конкретного применения.Вот как это работает. На первом экране определения размеров и выбора инженеры должны ввести четыре важных элемента информации: 1. Тип или ориентация редуктора (рядный или прямой угол). Угловые редукторы предлагают три отдельных варианта: стандартный вал, сдвоенный вал и полый вал. 2. Тип приложения. Пользователи выбирают между «циклическим режимом» и «непрерывным режимом». Любая операция, которая выполняется в одном направлении в течение 4 часов или более без остановки или изменения скорости, считается непрерывной работой.Все другие приложения, включая машины, которые работают более 4 часов, но меняют направление, считаются циклическими. 3. Требования к люфту делятся на три класса: 4. Коэффициент. На этом этапе инструмент показывает пользователям доступные коэффициенты для указанных комбинаций. Например, если выбрать линейную ориентацию, соотношения 1: 1 и 2: 1 будут «затенены», потому что они доступны только в прямоугольных версиях. Далее у пользователей есть два способа ввести требования к крутящему моменту и скорости. Первый вариант — ввести их как максимальный крутящий момент и число оборотов в минуту. Можно ввести либо входную, либо выходную частоту вращения, и инструмент рассчитает другую. Для более сложных приложений пользователи могут создать полный профиль движения. Для каждого сегмента профиля движения требуются: скорость в начале и конце сегмента, продолжительность и крутящий момент во время сегмента. После указания этих параметров пользователи могут ввести радиальные или осевые нагрузки, которые могут присутствовать. Выбор крепления двигателя — последний шаг. Крепления доступны от более 300 производителей. Пользователи просто выбирают двигатель из раскрывающегося меню, и инструмент генерирует номер детали для монтажа двигателя.Размеры двигателя также будут указаны на экране для справки. Если нужный двигатель отсутствует в списке, инструмент имеет возможность вручную ввести размеры двигателя. Критические размеры, такие как диаметр и длина вала, окружность болта и диаметр пилота, используются для определения номера комплекта для монтажа двигателя, необходимого для редуктора. Пользователи могут вводить размеры в английских или метрических единицах. После ввода всех параметров приложения инструмент суммирует доступные редукторы, соответствующие критериям применения, отсортированные по цене от самых экономичных до самых дорогих.В нем также указан коэффициент безопасности между требуемым крутящим моментом и номинальным крутящим моментом каждого редуктора. После выбора продукта пользователи могут загрузить 2D- или 3D-модель, запросить ценовое предложение или сохранить выбор. Режим «Выбрать редуктор по номеру модели» можно использовать, когда требуемый редуктор уже известен. Он позволяет пользователям просматривать цены, спецификации каталога и сроки выполнения заказа, а также загружать модели САПР. Дизайнеры нажимают на семейство редукторов и выбирают тип продукта, размер рамы, передаточное число и комплект для монтажа двигателя.Если комплект для монтажа двигателя неизвестен, пользователи могут ввести размеры, как описано выше. © 2012 Penton Media, Inc. Введение — планетарные шестерни также называют планетарными шестернями, состоящими из трех элементов солнечной шестерни, планетарной шестерни и коронной шестерни. Солнечная шестерня расположена в центре, которая передает крутящий момент на планетарные шестерни, вращающиеся вокруг солнечной шестерни. Обе системы расположены внутри зубчатого венца. В зубчатой формации солнечная и планетарная шестерни зацеплены снаружи, а коронная шестерня — внутри.(См. Рис.01) Рис. 01 Диаметр шага коронной шестерни с 96 зубьями и 1 модулем. фиксированная шестерня ведущая шестерня ведомая шестерня число оборотов s1 число оборотов s2 число вращения число оборотов оси p1, p2 с2 а s1 p2s1 + p1s2 / p2s1 0 1 с2 / p2 с1 а с2 0 п2с1 + п1с2 / п1с2 1 с1 / п1 с2 s1 а 1 0 п2с1 / п2с1 + п1с2 p2s1 / p2s1 + p1s2 * s2 / p2 с1 с2 а 0 1 п1с2 / п2с1 + п1с2 п1с2 / п2с1 + п1с2 * с1 / п1
Gear Systems | Инженеры Edge
Уравнения и калькуляторы планетарных эпициклических передаточных чисел
F = Вращение ведомого, ведомой шестерни или шкива за один оборот привода. Обратите внимание на (F = вращение толкателя планетарного типа вокруг своей оси.) Или множитель отношения скорости толкателя к приводу.
A = Размер ведущей шестерни с использованием либо числа зубьев, либо делительного диаметра. Примечание. Когда ведомый элемент получает свое движение как от A, так и от вторичного ведущего элемента, A = размер начальной ведущей шестерни, а формула дает соотношение скоростей между A и ведомым элементом.
B = размер ведомой шестерни или ведомого колеса (используйте либо делительный диаметр (дюймы или мм), либо общее количество зубьев)
C = размер фиксированной шестерни (используйте либо делительный диаметр, либо количество зубьев)
E = Угол в градусах
x = размер планетарной шестерни, как показано на диаграмме (используйте либо делительный диаметр, либо количество зубьев)
y = размер планетарной шестерни, как показано на схеме (используйте либо делительный диаметр, либо количество зубьев)
z = размер вторичной или вспомогательной ведущей шестерни, когда ведомый движется от двух приводных элементов
S = Вращение вторичного привода на один оборот первичного привода.S отрицательно, когда вторичный и начальный драйверы вращаются в противоположных направлениях. (Формулы, в которых используется S, дают соотношение скоростей между ведомым и начальным водителем.)
RPM = число оборотов в минуту.
Все права защищены
Отказ от ответственности
| Контакты Вывод уравнения Уиллиса (основное уравнение планетарных шестерен)
Наложение движений
1 2 3 Движение водило Движение планетарной шестерни Полное движение Вращение водила вокруг солнечной шестерни
\ label {P1}
& \ underline {\ varphi_ {p1} = \ varphi_c} \\ [5px]
\ end {align} Вращение планетарной шестерни вокруг собственного центра тяжести
& b_ {p2} = b_c \\ [5px]
& \ tfrac {d_p} {2} \ cdot \ varphi_ {p2} = \ tfrac {d_s} {2} \ cdot \ varphi_c \\ [5px]
\ label {P2}
& \ underline {\ varphi_ {p2} = \ frac {d_s} {d_p} \ cdot \ varphi_c} \\ [5px]
\ end {align} Вращение солнечной шестерни
& b_ {p3} = — b_s \\ [5px]
& \ tfrac {d_p} {2} \ cdot \ varphi_ {p3} = — \ tfrac {d_s} {2} \ cdot \ varphi_s \\ [5px]
\ label {P3}
& \ underline {\ varphi_ {p3} = — \ frac {d_s} {d_p} \ cdot \ varphi_s} \\ [5px]
\ end {align} Наложение различных движений
& \ varphi_p = \ varphi_ {p1} + \ varphi_ {p2} + \ varphi_ {p3} \\ [5px]
\ label {P}
& \ underline {\ varphi_ {p} = \ cdot \ varphi_c + \ frac {d_s} {d_p} \ cdot \ varphi_c — \ frac {d_s} {d_p} \ cdot \ varphi_s} \\ [5px]
\ end {align}
& \ varphi = \ omega \ cdot t ~~~ \ text {with} ~~~ \ omega = 2 \ pi \ cdot n ~~~ \ text {применяется:} \\ [5px]
\ label {varp}
& \ underline {\ varphi = 2 \ pi \ cdot n \ cdot t} \\ [5px]
\ end {align}
& 2 \ pi \ cdot n_p \ cdot t = 2 \ pi \ cdot n_c \ cdot t + \ frac {d_s} {d_p} \ cdot 2 \ pi \ cdot n_c \ cdot t — \ frac { d_s} {d_p} \ cdot 2 \ pi \ cdot n_s \ cdot t \\ [5px]
& n_p = n_c + \ frac {d_s} {d_p} \ cdot n_c — \ frac {d_s} {d_p} \ cdot n_s ~ ~~~~~~~ \ text {|} \ cdot d_p \\ [5px]
& n_p \ cdot d_p = n_c \ cdot d_p + d_s \ cdot n_c — d_s \ cdot n_s \\ [5px]
\ label {g }
& \ в коробке {n_p \ cdot d_p = n_c \ cdot \ left (d_p + d_s \ right) — n_s \ cdot d_s} \\ [5px]
\ end {align}
\ label {pln}
& \ boxed {n_p \ cdot z_p = n_c \ cdot \ left (z_p + z_s \ right) — n_s \ cdot z_s} \\ [5px]
\ end {align } — Обзор основных критериев проектирования и новые варианты выбора размеров
• Лучшее распределение нагрузки, что увеличивает срок службы.
• Более плавная и тихая работа.
• Люфт снижен на 2 угл. Мин. Шум редуктора
Редуктор трения
Уплотнение редуктора
Смазка редуктора
• Максимальный люфт Ultraprecision составляет 4 мин. Дуги для одноступенчатых устройств и 5 мин. Дуги для двухступенчатых.
• Высокая точность имеет максимальный люфт 8 угловых минут (одноступенчатый) и 9 угловых минут (двухступенчатый).
• Класс точности имеет максимальный люфт 13 и 15 угловых минут для одно- и двухступенчатых устройств соответственно. Планетарная передача: 8 ступеней
Планетарная передача встречается во многих вариантах и конфигурациях, чтобы соответствовать широкому диапазону передаточных чисел в соответствии с требованиями конструкции. Планетарная зубчатая передача используется в различных приложениях, таких как часы, лунный календарь, автомобильное зеркало, игрушки, мотор-редуктор, газотурбинный двигатель и многое другое.
Для подробного понимания планетарной шестерни: http://en.wikipedia.org/wiki/Epicyclic_gearing Planetary Gear Design.
Планетарная шестерня не будет собрана, если количество зубьев в каждой шестерне не будет выбрано должным образом.
Передаточное отношение планетарного цилиндрического цилиндрического зубчатого колеса 5: 1 означает, что солнечная шестерня должна совершать 5 оборотов за каждый оборот выходного водила.
Желаемое количество зубьев солнечной шестерни — 24.
Требования к конструкции:
Передаточное отношение = 5: 1
Солнечная шестерня = 24
Модуль = 1
Так как я работаю в метрических единицах, все размеры будут в мм. При выборе шестерен в метрических единицах профиль зуба прямозубой шестерни будет в модуле.
M = модуль
N = количество зубьев
Nr = количество зубьев коронной шестерни
Pd = диаметр шага
R = передаточное отношение
PDs = N / M = 24/1 = 24 мм Ур.01
Диаметр шага солнечной шестерни составляет 24.
Рассчитайте количество зубьев, необходимых в коронной шестерне для передаточного числа 5: 1.
R = 1 + Nr / Pd Ур. 02
Решите для Nr
Nr = Pd (R-1) = 24 (5-1) = 24 (4) = 96 зубьев
Pd = Nr / M Ур. 03 Pd = 96/1 = 96 мм
Диаметр шага планетарных шестерен должен быть определен от.
PDp = (Nr-PDs) / 2 = (96-24) / 2 = 72/2 = 36 мм
Количество зубьев планетарной шестерни теперь можно узнать из.
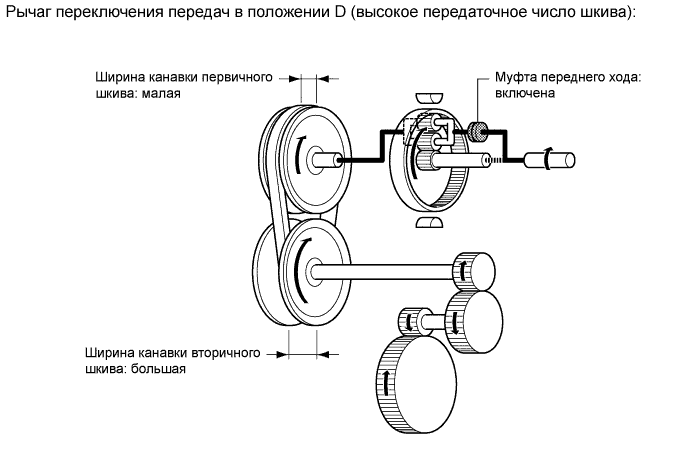 При этом нагрузка в каждом зацеплении уменьшается в несколько раз;
При этом нагрузка в каждом зацеплении уменьшается в несколько раз;