Модуль сдвига (упругости II рода)
Модулем сдвига (модуль упругости II рода, модуль упругости при сдвиге) – называется физическая величина, характеризующая упругие свойства материалов и их способность сопротивляться сдвигающим деформациям.
Обозначается латинской буквой G,
единица измерения – Паскаль [Па] (гигапаскаль [ГПа])
В сопромате данный модуль используется в расчетах на сдвиг, срез и кручение.
Рис. 1 Деформация сдвига
Теоретически определяется отношением касательных напряжений τ к углу сдвига γ (рис. 1)
где
τ=F/A — касательные напряжения;
γ — угол сдвига;
F — сдвигающая сила;
A — площадь приложения силы F;
ΔS — величина сдвига;
a — размер элемента.
Опытное значение определяется по результатам эксперимента по определению модуля упругости II рода.
Таблица 1. Сравнительные значения модуля для некоторых материалов
Материал | Модуль сдвига |
Сталь | 80 |
Чугун | 45 |
Медь | 40 |
Титан | 40 |
Алюминий | 27 |
Стекло | 26,2 |
Модуль упругости II рода можно определить с помощью известных модуля Юнга E и коэффициента Пуассона ν:
Модуль сдвига является коэффициентом пропорциональности в законе Гука при сдвиге:
τ=Gγ
При расчетах на кручение, GIp – жесткость поперечного сечения вала, где Ip — полярный момент инерции поперечного сечения.
Механические характеристики материалов >
Примеры решения задач >
Определение модуля сдвига при испытании на кручение
Цель
работы. Экспериментальное
определение модуля сдвига стали
и
алюминиевого сплава Д16-Т.
1. Краткие теоретические сведения.
Расчеты
на сдвиг (срез) выполняются для таких
элементов конструкций, как сварные швы,
заклепки, болты и др. При деформации
сдвига возникают касательные напряжения
τ,
которые
по закону Гука пропорциональны углу
сдвига γ:
,
где
– модуль сдвига (модуль упругости
второго рода).
Модуль
сдвига
связан с модулем продольной упругости
(модулем упругости первого рода)
соотношением:
где
– коэффициент поперечной деформации
(коэффициент
Пуассона),
для сталей
=0,25
… 0,30.
Частным
случаем чистого сдвига являются
деформации кручения валов и стержней
круглого поперечного сечения. Однако
в случае кручения удобнее фиксировать
не угол сдвига материала, а угол
закручивания стержня φ.
Закон
Гука при кручении стержней круглого
поперечного сечения выражается формулой
,
где
—
угол закручивания или угол поворота
одного сечения
стержня
относительно другого (рад),
0
— расстояние между этими сечениями,
—
крутящий момент, передаваемый на
стержень,
—
полярный момент инерции поперечного
сечения стержня.
Зная
величину
0
и вычислив полярный момент инерции
сечения стержня
,
можно по замеренному углу закручивания
,
соответствующему заданной моментной
нагрузке, вычислить значение величины
по формуле
2.
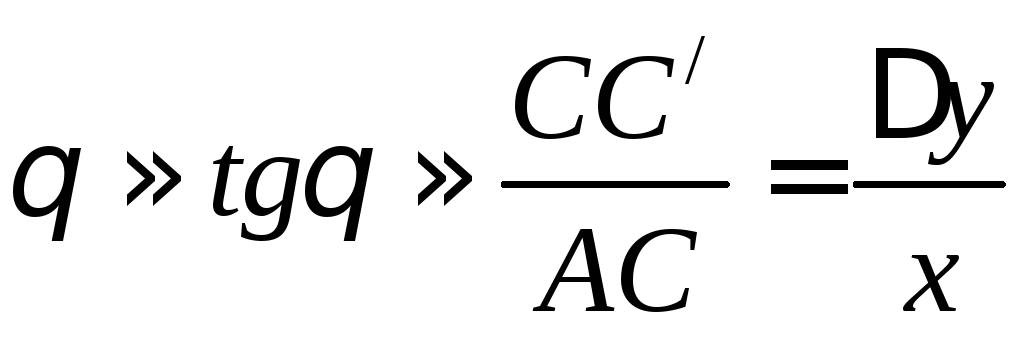 Применяемая установка и приборы
Применяемая установка и приборы
Для
проведения работы используется наладка
универсального лабораторного стенда
по сопротивлению материалов СМ-2 (рис.
1).
Исследуемый
образец 1 в виде ступенчатого трубчатого
стержня, узкая часть которого выполнена
из стали, а широкая из алюминиевого
сплава Д16-Т (рис. 2), жестко соединяется
со стойкой, выполненной в виде опоры
типа «заделка». Противоположный конец
образца имеет шарнирную опору, которая
создается шарикоподшипником, опирающимся
на другую стойку (на схеме не показаны).
Нагружение осуществляется грузами,
подвешиваемыми к концу рычага 2. Рычаг
служит для нагружения образца крутящим
моментом, величина которого:
где
– вес грузов, Н;
– длина
рычага, м.
Измерение
угла закручивания
одного
сечения относительно другого производится
на рабочей части образца длиной
,
где при помощи неподвижных захватов
закреплен измеритель. Один из захватов
имеет неподвижный кронштейн 6, на котором
установлен индикатор часового типа 4.
Другой захват имеет жесткую скобу 3, в
которую упирается ножка индикатора 4.
При
повороте сечения В относительно сечения
С индикатор фиксирует изменение величины
.
ЗнаяиН,
можно вычислить искомый угол закручивания
образца между этими сечениями:
Основные
размеры установки:
Длина
рычага a
= 100 мм; длина образца L
= 240 мм;
длина
рабочей части образца l0
=
100 мм;
расстояние
от оси образца до ножки индикатора H
= 80 мм, наружный диаметр трубы из сплава
Д16-Т D
= 42 мм;
внутренний
диаметр трубы из сплава Д16-Т D1=
40 мм;
наружный
диаметр стальной трубы d
= 20 мм,
внутренний
диаметр стальной трубы d1
= 16 мм.
Рис.
1. Схема экспериментальной установки:
1
— ступенчатый стержень трубчатого
сечения (участок ВС
выполнен
из стали, ДК – из алюминиевого сплава
Д16-Т) , 2-грузовой
рычаг, 3—
скоба, 4—
индикатор часового типа, 5—
розетка тензорезисторов, 6
– кронштейн.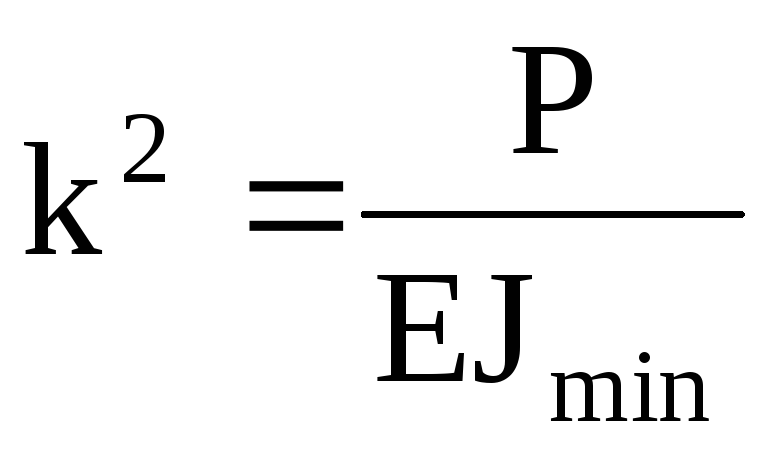
стальная
труба Вид
К
Алюминивая
труба
Рис.
2. Сечениястержня Рис. 3. Схема
наклейки тензорезисторов
Рассмотрим
элемент на поверхности бруса, который
находится в напряженном состоянии
«чистый сдвиг». Расчетное касательное
напряжение
(где-
крутящий момент, передаваемый на образец,- полярный момент сопротивления кручению).
Для
определения модуля сдвига участка
стержня сплава Д16-Т в выбранной точке
на поверхности образца (вид по стрелке
К) наклеиваются три проволочных датчика
сопротивления, составляющих розетку
по схеме, приведенной на рис. 3.
Поскольку
при кручении в сечениях, перпендикулярных
оси стержня возникают касательные
напряжения τ,
а
по сечениям, наклоненным к оси на угол
45º, действуют главные напряжения
и
,
то
деформации в направлении осей u
и
v
на
рис. 3
и
будут
главными. Используя тензометрический
метод, главные напряжения на поверхности
трубы из сплава Д16-Т найдем через главные
деформации.
Определим
продольную деформацию в диагональном
направлении (под углом 450
к оси бруса), как отношение удлинения
диагонали
∆ℓ =
к ее первоначальной
длине ℓ0
=(рис.
4). В результате получим:
В
направлении другой диагонали деформация
будет отличаться только знаком, т.е.
или.
Рис.
4. Схема деформации стержня в точке
наклейки
тензорезисторов
В
результате модуль сдвига сплава Д16-Т
может быть определен по формуле:
где
и– продольные деформации, определяемые
электротензометрическим методом.
Модуль сдвига (модуль упругости II рода)
Здесь т — касательное напряжение rfs — элемен контура, ограничивающего профиль О—модуль сдвига (модуль упругости второго рода) F—площадь, ограниченная контуром средней линии стенки Gj—угол закручивания на единицу длины (погонный угол кручения).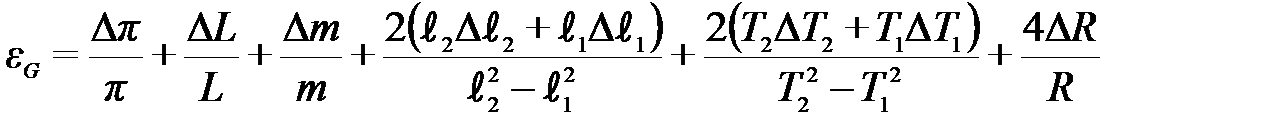 [c.154]
[c.154]
Модуль упругости второго рода имеет размерность напряжения, так как относительный сдвиг является величиной безразмерной. Величины модулей упругости первого и второго рода связаны следующей формулой, вывод которой здесь не приводится [c.186]
Отсюда найдем зависимость между модулем сдвига G и модулем упругости первого рода
[c.86]
Коэ( Я )ициент пропорциональности О характеризует жесткость материала при сдвиге, т. е. его способность сопротивляться упругой деформации сдвига он называется модулем сдвига, или модулем упругости второго рода. Из формулы (2. 19) следует, что О измеряется в тех же единицах, что и напряжение, так как у — величина отвлеченная. [c.243]
Коэффициент пропорциональности G носит название модуля сдвига, или модуля упругости второго рода. Если представить [c.228]
Коэффициент пропорциональности О характеризует жесткость материала (т. е. способность сопротивляться упругим деформациям) при сдвиге и называется модулем сдвига или модулем упругости второго рода. [c.210]
Е, О—модули упругости первого рода (модуль Юнга) и второго рода (модуль сдвига) х — коэффициент Пуассона [c.12]
По аналогии с законом Гука для линейной деформации дается закон Гука, аля угловой деформации (при сдвиге). Разъясняется физический смысл модуля сдвига О как физической постоянной материала, характеризующей его жесткость при сдвиге. В учебной литературе и в практике преподавания для величины О применяют различные наименования модуль сдвига, модуль упругости при сдвиге, модуль упругости второго рода. Не отрицая возможности применения любого из этих терминов, будем пользоваться первым из них как рекомендованным Комитетом технической терминологии АН СССР. [c.103]
ЧИСТЫЙ сдвиг. ЗАВИСИМОСТЬ МЕЖДУ МОДУЛЯМИ УПРУГОСТИ ПЕРВОГО Е И ВТОРОГО О РОДА
[c. 82]
82]
Формула (6.6.1) носит название закона Гука при сдвиге. Величина О, имеющая размерность напряжения, называется модулем сдвига, или модулем упругости второго рода. [c.82]
Величина О носит название модуля сдвига или модуля упругости второго рода. Ввиду того, что относительный сдвиг — величина безразмерная, модуль сдвига имеет размерность напряжения, т. е. измеряется в МПа. [c.104]
О — модуль упругости 2-го рода материала тела, р — угол сдвига, который является мерой деформации сдвига. [c.110]
Е, G —модуля упругости первого рода (модуль Юнга) и второго рода (модуль сдвига)
[c.10]
Коэффициент пропорциональности G в формулах (4.3) и (4.4) называется модулем сдвига (или модулем упругости второго рода). [c.125]
Коэффициент пропорциональности в уравнении (1П.5) обозначается через С и называется модулем поперечной упругости (модулем упругости при сдвиге, модулем упругости второго рода) [c.86]
Между модулем сдвига G, модулем упругости первого рода Е и коэффициентом Пуассона существует следующая зависимость [c.108]
Величина G, входящая в формулы (78) и (79), называется модулем упругости при сдвиге или модулем упругости второго рода. Так как у—величина отвлеченная, то из (79) легко заключить, что размерность G будет такая же, как и напряжения, т.е. /сГ/сл Между величинами Е и G для одного и того же материала имеется следующее соотношение [c.113]
Если пластина относительно толстая или модуль сдвига по толщине очень мал по сравнению с модулем упругости в плоскости пластины (типичный случай для — композиционных материалов), то могут нарушаться гипотезы Кирхгоффа, используемые для тонких пластин. Тогда вместо классической теории пластин можно использовать уточненную теорию, учитывающую сдвиг по толщине, или непосредственно трехмерную теорию упругости.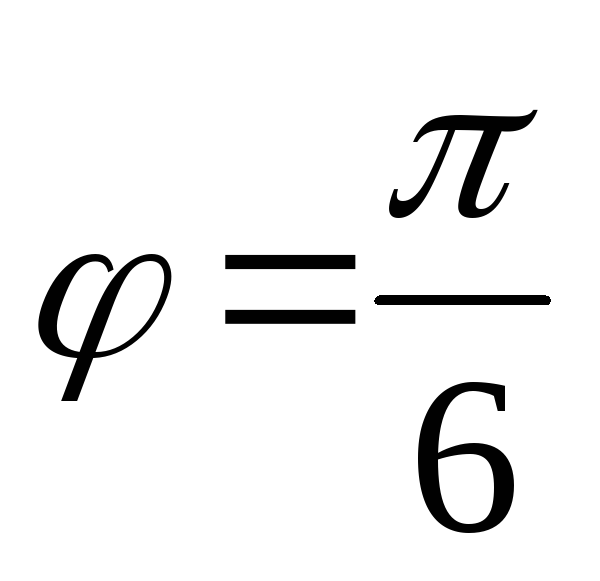 Теории такого рода, а также теория трехслойных пластин описаны в разделах VI и VII.
[c.158]
Теории такого рода, а также теория трехслойных пластин описаны в разделах VI и VII.
[c.158]
V — коэффициент Пуассона G — модуль упругости второго рода Ki, Ki — коэффициенты интенсивности напряжений соответственно для растяжения и сдвига, которые можно представить как [c.102]
Здесь Е — модуль упругости первого рода (модуль продольной упругости) G — модуль упругости второго рода (модуль сдвига) /-1 — безразмерный коэффициент поперечной деформации, или коэффициент Пуассона. Эти три величины связаны зависимостью [c.267]
Также, если в формуле, выведенной на основе теории упругости, имеется модуль упругости второго рода G (модуль сдвига), то его следует заменить через модули Е w К. [c.119]
G — модуль упругости второго рода (модуль сдвига). [c.9]
Закон Гука для сдвига у=т/0, где т — касательное напряжение у—относительный сдвиг (угол сдвига) (3 — модуль упругости второго рода (рис. 10.3, в). [c.186]
Сила Р, растягивающая пружину, считается положительной. Сила, сжимающая пружину, считается отрицательной. В формулах (4.286), (4.306) и (4.316) ja — коэффициент Пуассона, вошедший в формулы при замене модуля сдвига G модулем упругости первого рода Е [то же. в формулах (4.28г), (4.30г) и (4.31г) — табл. 4.4 ]. [c.83]
В пределах упругости (до точки УИпц кривой кручения) определяется модуль сдвига (модуль П рода, модуль касательной упругости) О как [c.42]
При определении главных угловых дефсфмации используем закон Гука в форме соотношения у = т / С, для чего необходимо вычислить модуль сдвига (модуль упругости второго рода) [c.29]
Величина G, входящая в формулу (3.18), называется модулем упругости при сдвиге или модулем упругости второго рода. Размерность G выражается в кгс1см . [c.103]
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Упругие свойства тел
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) — (α)
μ = (E / 2G) — 1 — (b)
K = E / 3(1 — 2μ) — (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
Материал при 18°С | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
Алюминий | 7,05 | 2,62 | 0,345 | 7,58 |
Висмут | 3,19 | 1,20 | 0,330 | 3,13 |
Железо | 21,2 | 8,2 | 0,29 | 16,9 |
Золото | 7,8 | 2,7 | 0,44 | 21,7 |
Кадмий | 4,99 | 1,92 | 0,300 | 4,16 |
Медь | 12,98 | 4,833 | 0,343 | 13,76 |
Никель | 20,4 | 7,9 | 0,280 | 16,1 |
Платина | 16,8 | 6,1 | 0,377 | 22,8 |
Свинец | 1,62 | 0,562 | 0,441 | 4,6 |
Серебро | 8,27 | 3,03 | 0,367 | 10,4 |
Титан | 11,6 | 4,38 | 0,32 | 10,7 |
Цинк | 9,0 | 3,6 | 0,25 | 6,0 |
Сталь (1% С) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
(мягкая) | 21,0 | 8,12 | 0,291 | 16,78 |
Константан 2) | 16,3 | 6,11 | 0,327 | 15,7 |
Манганин | 12,4 | 4,65 | 0,334 | 12,4 |
1) Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке. 2) 60% Cu, 40% Ni. | ||||
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
Вещество | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
Бронза (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
Медь | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
Нейзильбер1) | 11,6 | 4,3-4,7 | 0,37 | — |
Стекло | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
Стекло иенское крон | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
Стекло иенское флинт | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
Железо сварочное | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
Чугун | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
Магний | 4,25 | 1,63 | 0,30 | — |
Бронза фосфористая2) | 12,0 | 4,36 | 0,38 | — |
Платиноид3) | 13,6 | 3,6 | 0,37 | — |
Кварцевые нити (плав. | 7,3 | 3,1 | 0,17 | 3,7 |
Резина мягкая вулканизированная | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | — |
Сталь | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
Цинк | 8,7 | 3,8 | 0,21 | — |
1) 60% Cu, 15% Ni, 25% Zn 2) 92,5% Cu, 7% Sn, 0,5% P 3) Нейзильбер с небольшим количеством вольфрама. | ||||
Вещество | Модуль Юнга E, 1011 дин/см2. | Вещество | Модуль Юнга E, 1011 дин/см2. |
Цинк (чистый) | 9,0 | Дуб | 1,3 |
Иридий | 52,0 | Сосна | 0,9 |
Родий | 29,0 | Красное дерево | 0,88 |
Тантал | 18,6 | Цирконий | 7,4 |
Инвар | 17,6 | Титан | 10,5-11,0 |
Сплав 90% Pt, 10% Ir | 21,0 | Кальций | 2,0-2,5 |
Дюралюминий | 7,1 | Свинец | 0,7-1,6 |
Шелковые нити1 | 0,65 | Тиковое дерево | 1,66 |
Паутина2 | 0,3 | Серебро | 7,1-8,3 |
Кетгут | 0,32 | Пластмассы: |
|
Лед (-20С) | 0,28 | Термопластичные | 0,14-0,28 |
Кварц | 7,3 | Термореактивные | 0,35-1,1 |
Мрамор | 3,0-4,0 | Вольфрам | 41,1 |
1) Быстро уменьшается с увеличением нагрузки 2) Обнаруживает заметную упругую усталость | |||
Температурный коэффициент (при 150С) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Сжимаемость k, бар-1 | |||
| ɑ, для Е | ɑ, для G |
|
|
Алюминий | 4,8*10-4 | 5,2*10-4 | Алюминий | 1,36*10-6 |
Латунь | 3,7*10-4 | 4,6*10-4 | Медь | 0,73*10-6 |
Золото | 4,8*10-4 | 3,3*10-4 | Золото | 0,61*10-6 |
Железо | 2,3*10-4 | 2,8*10-4 | Свинец | 2,1*10-6 |
Сталь | 2,4*10-4 | 2,6*10-4 | Магний | 2,8*10-6 |
Платина | 0,98*10-4 | 1,0*10-4 | Платина | 0,36*10-6 |
Серебро | 7,5*10-4 | 4,5*10-4 | Стекло флинт | 3,0*10-6 |
Олово | — | 5,9*10-4 | Стекло немецкое | 2,57*10-6 |
Медь | 3,0*10-4 | 3,1*10-4 | Сталь | 0,59*10-6 |
Нейзильбер | — | 6,5*10-4 |
|
|
Фосфористая бронза | — | 3,0*10-4 |
|
|
Кварцевые нити | -1,5*10-4 | -1,1*10-4 |
|
|
Лабораторная работа 104
Цель работы: Экспериментальное
определение модуля кручения и модуля сдвига стальной проволоки методом
крутильных колебаний.
Приборы и принадлежности:
крутильный маятник, секундомер, штангенциркуль, измерительная линейка,
технические весы.
Теоретическое введение
Как показывает опыт, при воздействии на тело внешних сил оно меняет
форму и размеры, т.е. наблюдается механическая деформация. В физике рассматриваются
наиболее простые виды деформации: растяжение, сжатие, изгиб, сдвиг, кручение.
Пусть имеем тело в
форме прямоугольного параллелепипеда, закрепленного в своей нижней части, и
мысленно разделим его на ряд слоев, параллельных основанию (рис.1). Если к
верхней плоскости параллелепипеда приложить силу , касательную к этой плоскости, то тело деформируется –
одни слои будут двигаться относительно других, оставаясь параллельными друг
другу, причем, боковые грани параллелепипеда останутся плоскостями,
параллельными друг другу. Такая деформация является чистым сдвигом и
характеризуется углом сдвига j
,
где
d – толщина тела, а bb/– абсолютная
величина сдвига верхнего слоя относительно нижнего.
Касательная
сила dFt, приходящаяся на единицу
площади поверхности, на которую действует эта сила, называется касательным
механическим напряжением t :
,
где
dFt— касательная к
поверхности dS сила.
Если
угол j мал, то tgj=j =, угол сдвига, j называют относительным сдвигом, выражаемым в
радианах. По закону Гука относительный сдвиг j пропорционален
касательному напряжению τ:
где
G – модуль сдвига, [Н/м2]. Модуль сдвига равен касательному напряжению,
Модуль сдвига равен касательному напряжению,
необходимому для изменения угла сдвига на единицу (j=1).Модуль сдвига зависит от
рода, температуры и кристаллической структуры вещества.
Перейдем далее к деформации
кручения. Рассмотрим образец в виде цилиндрического стержня длиной L и радиусом r (рис.2). Пусть нижнее
основание образца закреплено неподвижно, а к верхнему
приложен момент пары сил , закручивающий верхний конец образца против часовой
стрелки.
Момент пары
сил, вызывающий кручение стержня, называется крутящим моментом. Для небольших
деформаций любого типа справедлив закон Гука, поэтому применительно к
кручению можно записать:
где модуль кручения D равен моменту сил,
вызывающему закручивание стержня на единичный угол. [D]=Н×м.
Поскольку
деформация кручения представляет собой одновременные действия сдвига и сжатия
(или растяжения), то между модулем кручения D и сдвига G
существует количественная связь, которую можно определить следующим образом.
Пусть
однородный стержень радиусом R
и длиной l0 сделан из материала, модуль сдвига которого
равен G и закручен моментом сил M0 на угол a0 (рис.3а). Вырежем из
стержня длиной l0 диск достаточно малой высоты dl на расстоянии l от неподвижного
основания. Положим, что нижнее основание этого диска неподвижно, а верхнее –
повернулось на бесконечно малый угол da. Тогда бесконечно малый
угол сдвига dj
можно определить из геометрии
и
Тогда
Вырежем
кольцо радиусом r
и толщиной dr (рис. 3,б) из диска толщиной dl. Определим касательное напряжение t, действующее на
3,б) из диска толщиной dl. Определим касательное напряжение t, действующее на
поверхность кольца, из закона Гука.
Тогда касательная сила, действующая на поверхность кольца, равна
где
dS=2πrdr – площадь поверхности
кольца. С учетом (4) и (5) можно записать в виде:
Момент
этой силы относительно оси равен:
Тогда момент сил по всей поверхности диска равен:
Поскольку
стержень однородный, то деформация кручения однородная и для нее справедливо
соотношение:
С учетом (8) уравнение (7) можно записать в виде:
Сравнивая (9) с формулой (2), получим:
Если
осуществлять крутящий момент поворотом вокруг оси цилиндра ОО/ какой-либо
значительной массы, прикрепленной к свободному концу стержня, то согласно
основному уравнению динамики вращательного движения можно записать:
(11)
где J – момент инерции
вращающейся массы, d2a/dt2 – ее угловое ускорение.
Из формул (2) и (11)
имеем:
Обозначив получим
Соотношение
(12) является дифференциальным уравнением гармонических колебаний с частотой w. Период колебаний
Период колебаний
системы:
Из (13) находим модуль
кручения:
Описание рабочей установки и метода
измерений
Для
определения модуля кручения и модуля сдвига используется крутильный маятник.
К нижнему концу вертикально висящей проволоки 1 крепится горизонтально
висящий стержень 2 со средним грузом 3 и двумя равными грузами 4, массой m каждый, которые можно
перемещать вдоль стержня 2 (рис.4). Если сообщить этой системе небольшой
импульс в плоскости, перпендикулярной оси проволоки, то система начнет
совершать крутильные колебания, при которых проволока закручивается то в
одну, то в другую сторону. Такое устройство и является крутильным маятником.
Для
того чтобы избежать определения момента инерции системы J, входящего в формулу
(14), поступают следующим образом.
Устанавливают
каждый из грузов 4 сначала на расстоянии l1 от оси вращения, а потом на расстоянии l2 и определяют периоды
колебаний системы Т1 и Т2. Тогда
согласно формуле (13) для этих величин можно записать:
где
J1 и J2 – моменты инерции
системы относительно оси, совпадающей с осью проволоки, при удалении от нее
каждого подвижного груза соответственно на l1 и l2 . Согласно теореме Штейнера:
и ,
где
J1 и J2
– моменты инерции всех тел системы относительно осей, проходящих через центр
масс каждого тела.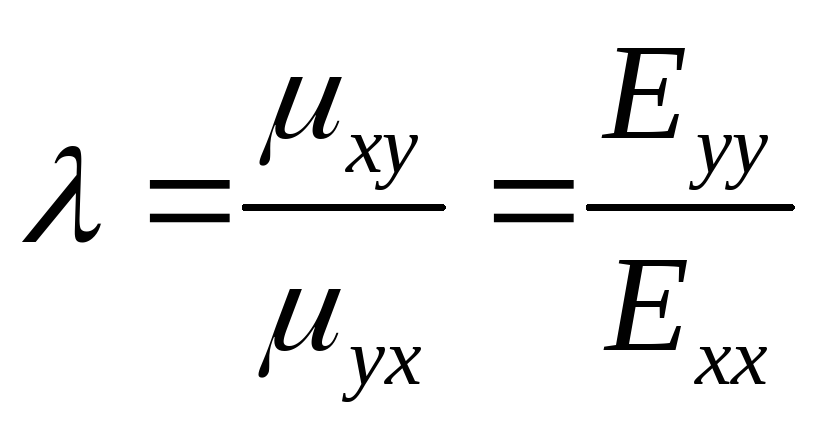
Найдя
разность и составив пропорцию с учетом
(15):
,
получим:
Подставляя (16) в (14), получим:
Выражение (17) является расчетной формулой при определении модуля кручения
проволоки 1. Зная модуль кручения D,
можно найти модуль сдвига G
проволоки из (10):
где L – длина проволоки, R – ее радиус.
Ход работы
1.
Расположить подвижные грузы на минимальном расстоянии от оси вращения
крутильного маятника. Измерить расстояние l1 от оси маятника до центра подвижного груза.
2.
Закручивают маятник на малый угол (не более 60)
относительно оси проволоки, после чего предоставляют его самому себе. Маятник
начинает совершать колебания в горизонтальной плоскости. Секундомером измерить
время t1 30-50 полных колебаний.
Опыт повторяют не менее 5 раз с одним и тем же выбранным числом колебаний. Находят
среднее значение < >. Определить период колебаний:
3.
где n
– число колебаний маятника.
4.
Раздвинуть подвижные грузы на максимальное расстояние от оси маятника.
Измерить расстояние l2
от оси маятника до центра подвижного груза.
5.
Определить период колебаний маятника T2 при раздвинутых грузах, измеряя время t2 не менее 5 раз для того
же числа колебаний n,
что и при измерении Т1.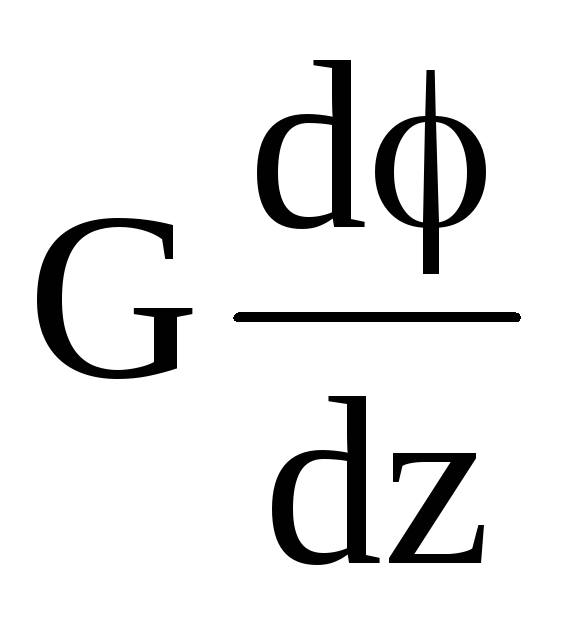
6.
По формуле (17) найти среднее значение модуля кручения <D>.
7.
Штангенциркулем измерить радиус проволоки r.
8.
По формуле (18) определить модуль сдвига материала проволоки. Длина
проволоки L = 1,82 м.
9.
Методом расчета погрешностей косвенных измерений найти абсолютные
погрешности результатов DD и DG.
10. Данные результатов
измерений и вычислений занести в таблицу.
Таблица результатов
|
n
|
m
|
l1
|
t1
|
T1
|
l2
|
t2
|
T2
|
<D>
|
r
|
G
|
DD
|
DG
|
|
|
кг
|
м
|
с
|
с
|
м
|
с
|
с
|
Н×м
|
м
|
Н×м2
|
Н×м
|
Н/м2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вопросы для допуска к
работе
1.
Какова цель работы?
2.
Опишите рабочую установку и ход эксперимента.
3.
Запишите рабочую формулу для определения модуля кручения. При каких
условиях справедлива эта формула?
4.
Оцените погрешность метода измерений модуля кручения и сдвига.
Вопросы для защиты работы
1.
Каков физический смысл модуля сдвига и модуля кручения?
2.
Сформулируйте теорему Гюйгенса – Штейнера и покажите, как она применяется
в проделанной работе.
3.
Выведите рабочие формулы для определения модуля кручения и модуля сдвига.
4.
Пользуясь дифференциальным методом, получите формулы относительных погрешностей
DD/D и DG/G.
5.
Как повысить точность результата эксперимента на данной установке?
6.
Какие виды деформации существуют?
7.
Что называется абсолютной и относительной деформацией?
8.
Запишите закон Гука для деформации сдвига и кручения.
9.
Выведите формулу (10).
10. Получите формулы (17) и
(18).
Измерение модуля упругости
Приложение:
Измерение модуля продольной упругости, модуля сдвига и коэффициента Пуассона (поперечной деформации) в недисперсионных изотропных конструкционных материалах.
Общие сведения:
Модуль Юнга (модуль продольной упругости) определяется как отношение напряжения (сила на единицу площади) к деформации сжатия.
Модуль сдвига определяется как отношение напряжения сдвига к деформации сдвига.
Коэффициент Пуассона отношение относительного поперечного сжатия к относительному продольному растяжению.
Эти основные свойства материалов обязательно учитываются в производстве и в различных научных исследованиях, и определяются с помощью измеренных значений скорости звука и плотности материала. Скорость распространения звука легко вычисляется путем ультразвукового контроля в режиме импульс-эхо с использованием соответствующего оборудования. Представленная ниже процедура действительна для любого однородного, изотропного, недисперсионного материала (скорость звука не изменяется с частотой). Сюда включены наиболее распространенные металлы, промышленная керамика и стекло, при условии, что размеры поперечного сечения не близки длине волны частоты контроля. Жесткие пластики, такие как полистирол и акрил, также могут быть измерены, несмотря на то, что они имеют высокий коэффициент затухания ультразвука.
Каучук не может быть измерен ультразвуковым методом по причине высокой степени дисперсии и нелинейно упругих свойств. Мягкие пластики точно так же показывают высокую степень затухания в режиме сдвиговых волн, и обычно не могут быть измерены. В случае анизотропных материалов, упругость варьируется в зависимости от направления, так же как и скорость распространения продольных волн и/или сдвиговых волн. Для генерации полной матрицы модуля упругости в анизотропных образцах обычно требуется шесть серий ультразвуковых измерений. Пористость или зернистость материала может влиять на точность измерения модуля упругости, поскольку вызывает колебания скорости звука исходя из размера и ориентации зерен или размера и распределения пор, вне зависимости от упругости материала.
Оборудование:
Для измерения скорости звука при расчете упругости обычно используются прецизионные толщиномеры 38DL PLUS или 45MG с ПО для одноэлементных ПЭП, или дефектоскопы с функцией измерения скорости звука (например, серии EPOCH). Генераторы/приемники модели 5072PR или 5077PR в комбинации с осциллографом или дискретизатором сигналов также могут использоваться для измерения времени распространения волн. Для данного теста потребуется два преобразователя, подходящих для эхо-импульсного измерения скорости звука в материале продольными и поперечными волнами. Среди наиболее используемых ПЭП: широкополосный преобразователь продольных волн M112 или V112 (10 МГц) и преобразователь поперечных волн с нормальным углом падения V156 (5 МГц). Они подходят для измерения наиболее распространенных металлов и обожженных керамических образцов. Для измерения очень толстых и очень тонких материалов или образцов с высоким затуханием ультразвука требуются специальные преобразователи. В некоторых случаях применяется теневой метод контроля (метод сквозного прозвучивания) с использованием двух преобразователей, расположенных на одной оси, по разные стороны проверяемого изделия. При выборе преобразователя или настройке прибора необходимо проконсультироваться со специалистом Olympus.
Для данного теста потребуется два преобразователя, подходящих для эхо-импульсного измерения скорости звука в материале продольными и поперечными волнами. Среди наиболее используемых ПЭП: широкополосный преобразователь продольных волн M112 или V112 (10 МГц) и преобразователь поперечных волн с нормальным углом падения V156 (5 МГц). Они подходят для измерения наиболее распространенных металлов и обожженных керамических образцов. Для измерения очень толстых и очень тонких материалов или образцов с высоким затуханием ультразвука требуются специальные преобразователи. В некоторых случаях применяется теневой метод контроля (метод сквозного прозвучивания) с использованием двух преобразователей, расположенных на одной оси, по разные стороны проверяемого изделия. При выборе преобразователя или настройке прибора необходимо проконсультироваться со специалистом Olympus.
Тестовый образец может быть любой формы, позволяющей выполнять эхо-импульсное измерение времени прохождения ультразвука через материал. Обычно, это образец толщиной 12,5 мм с ровными параллельными поверхностями, ширина или диаметр которого больше диаметра используемого преобразователя. Необходимо проявлять крайнюю осторожность при измерении узких образцов по причине возможных пограничных эффектов, которые могут повлиять на измеренное время прохождения импульса. При использовании сильно тонких образцов, разрешение будет ограничено из-за небольших колебаний во времени прохождения импульса через короткий УЗ-путь. Мы рекомендуем брать образцы толщиной минимум 5 мм, но желательно толще. Во всех случаях толщина тестового образца должна быть точно известна.
Процедура:
Измерьте скорость распространения продольных и сдвиговых волн тестового образца с использованием подходящих ПЭП и настроек прибора. Для измерения скорости сдвиговых волн потребуется специальная контактная жидкость высокой вязкости, как например SWC. Толщиномеры 38DL PLUS и 45MG могут напрямую измерять скорость звука в материале на основе введенной толщины образца, а дефектоскопы серии EPOCH измеряют скорость звука в ходе калибровки скорости звука. В обоих случаях, следуйте рекомендуемой процедуре измерения скорости звука, представленной в руководстве по эксплуатации прибора. При использовании генератора/приемника, зафиксируйте время прохождения сигнала туда и обратно через участок известной толщины с помощью преобразователей продольных и поперечных волн, и рассчитайте:
В обоих случаях, следуйте рекомендуемой процедуре измерения скорости звука, представленной в руководстве по эксплуатации прибора. При использовании генератора/приемника, зафиксируйте время прохождения сигнала туда и обратно через участок известной толщины с помощью преобразователей продольных и поперечных волн, и рассчитайте:
При необходимости, переведите единицы измерения скорости звука в дюйм/с или см/с. (Время обычно измеряется в микросекундах; для получения измерений в дюйм/с или см/с умножьте дюйм/мкс или см/мкс на 106.) Полученные значения скорости звука могут использоваться в следующих формулах.
Примечание: Если скорость звука выражена в см/с, а плотность – в г/см3, модуль упругости будет выражен в дин/см2. Если вы используете английскую систему мер (дюйм/с и фунт/дюйм3) для расчета модуля упругости в фунтах на кв. дюйм (PSI), не путайте фунт (единицу измерения силы) с фунтом (единицей измерения массы). Поскольку модуль упругости выражен как сила на единицу площади, при расчете в английской системе мер необходимо умножить результат вышеуказанной формулы на коэффициент пересчета масса/сила (1 / ускорение свободного падения) для получения значения упругости в фунтах на кв. дюйм. Если исходные расчеты выполнены в метрических единицах, используйте коэффициент конверсии 1 psi = 6,89 x 104 дин/см 2. Вы также можете ввести скорость звука в дюймах/с, а плотность – в г/см 3, а затем разделить на коэффициент пересчета 1,07 x 104 для получения упругости в PSI.
Для определения модуля сдвига умножьте квадрат скорости распространения поперечной волны на плотность.
Опять же, используйте единицы измерения см/с и г/см 3 для получения модуля упругости в дин/см2 или английскую систему мер (дюйм/с и фунт/дюйм3) и умножьте результат на коэффициент пересчета масса/сила.
Библиография
Подробнее об измерении модулей упругости ультразвуковым методом см.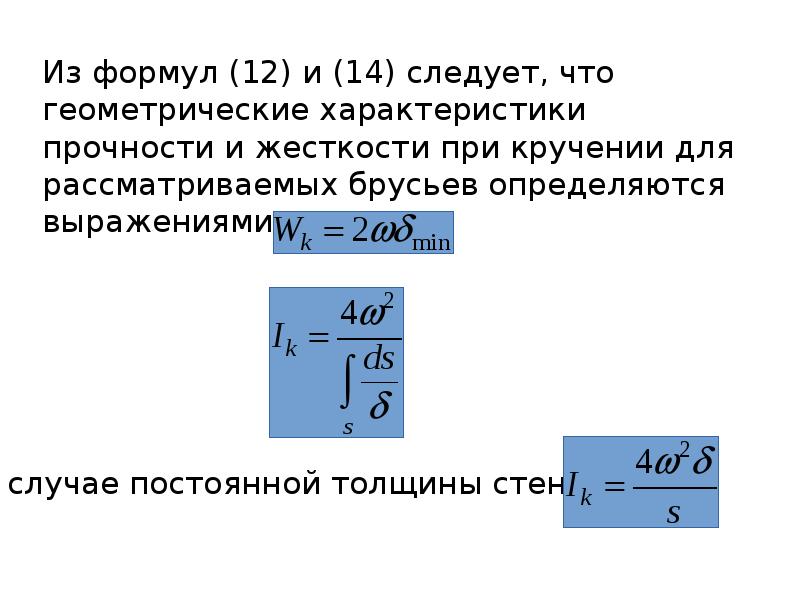 в представленных ниже источниках:
в представленных ниже источниках:
1. Moore, P. (ed.), Nondestructive Testing Handbook, Volume 7, American Society for Nondestructive Testing, 2007, pp. 319-321.
2. Krautkramer, J., H. Krautkramer, Ultrasonic Testing of Materials, Berlin, Heidelberg, New York 1990 (Fourth Edition), pp. 13-14, 533-534.
ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА С ПОМОЩЬЮ
ПРУЖИННОГО МАЯТНИКА
Стерлитамак
Цель работы – определение модуля сдвига материала пружины.
Приборы и принадлежности:установка лабораторная «Модуль Юнга и модуль сдвига ФМ 19», набор разновесов, набор пружин, штангенциркуль, линейка.
СОДЕРЖАНИЕ РАБОТЫ
Сдвигом называется деформация, при которой все плоские слои твердого тела, параллельные некоторой плоскости (плоскости сдвига), смещаются параллельно друг другу (рис. 1). Сдвиг происходит под действием силы F, приложенной параллельно плоскости сдвига ВС. Мерой деформации при этом является угол сдвига (относительный сдвиг). По закону Гука относительный сдвиг пропорционален касательному напряжению:
| , | (1) |
где S – площадь грани ВС, G – модуль сдвига, численно равный касательному напряжению, вызывающему относительный сдвиг, равный единице.
|
Рис. 1. Деформация сдвига |
Рис. 2. Геометрия пружины |
В данной работе определяется модуль сдвига материала, из которого изготовлена винтовая пружина (рис. 2). Основными геометрическими параметрами пружины являются диаметр проволоки d, диаметр витка пружины D и число витков N. Под действием растягивающей силы F длина пружины L увеличивается согласно закону Гука на величину
| , | (2) |
где k – жесткость пружины.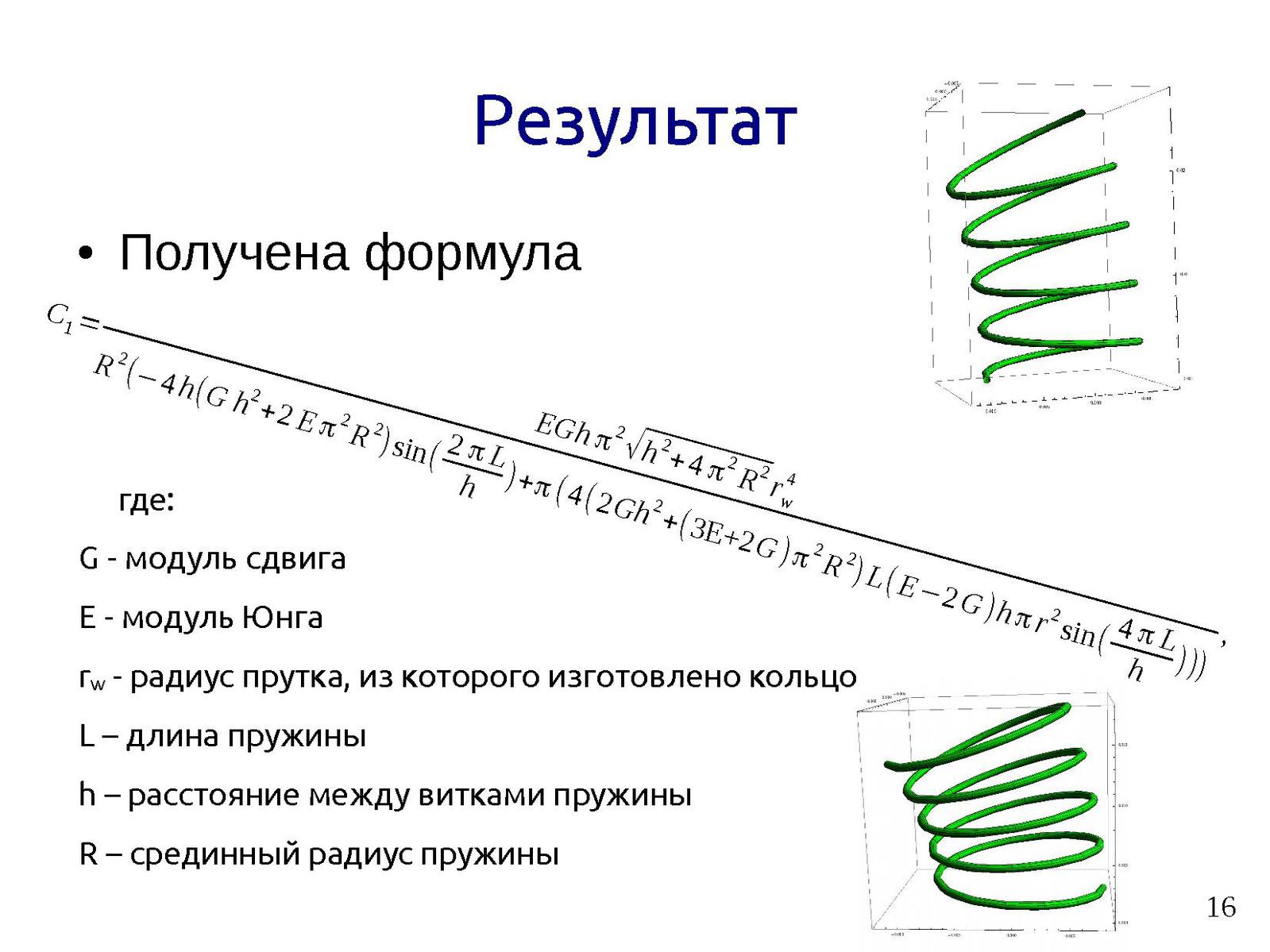 Направление действия силы при этом перпендикулярно виткам, поэтому удлинение пружины определяется модулем сдвига и дается соотношением
Направление действия силы при этом перпендикулярно виткам, поэтому удлинение пружины определяется модулем сдвига и дается соотношением
| . | (3) |
Рис. 3. Схема установки
Для определения модуля сдвига в работе используется пружинный маятник, показанный на рис. 3. На штативе 1 установлен кронштейн 2 с узлом крепления вертикально подвешенных сменных пружин 3. К пружине подвешивается наборный груз 4,. Измерение периодов колебаний груза производится с помощью фотодатчика 5.
Под действием сил тяжести и упругости пружины выведенный из положения равновесия груз массой m совершает гармонические колебания с частотой , периодом , откуда для жесткости пружины получаем:
| . | (4) |
Таким образом, измерив период колебаний и воспользовавшись формулами (2), (3), (4) с F=mg, можно найти модуль сдвига:
| . | (5) |
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1. Определение модуля сдвига с помощью пружинного маятника.
1. Кронштейн 2 с вертикально подвешенной пружиной 3 закрепить на вертикальной стойке 1 таким образом, чтобы наборный груз 4, подвешенный к пружине, своей нижней плоскостью совпадал с оптической осью фотодатчика 5 (оптическая ось совпадает с рисками на фотодатчике).
2. Оттянуть груз вниз и отпустить. При этом груз начинает совершать колебательные движения на пружине. Измерить время t для n=10…15 полных колебаний маятника. Запуск и остановка секундомера осуществляется фотоэлектрическим датчиком. При нажатии на клавишу «ПУСК» начинается отсчет времени от момента прохождения маятником положения равновесия. При нажатии клавиши «СТОП» секундомер фиксирует длительность t целого числа колебаний на момент ближайшего во времени прохождения маятником положения равновесия. Число колебаний фиксируется специальным индикатором. Найти период колебаний . Повторить опыт 4-5 раз.
Число колебаний фиксируется специальным индикатором. Найти период колебаний . Повторить опыт 4-5 раз.
3. Повторить задание п. 2, увеличивая массу груза. Всего провести измерения для 3-4 значений m.
4. Измерить параметры пружины D, d, N.
5. Для каждого значения m вычислить модуль сдвига G(т) по формуле (5). Найти усредненное значение G.
6. Данные измерений и вычислений внесите в таблицу.
Таблица 1.
| № | ,
кг | , м | , м | , c | , c | , c | , c | , c | ,
кг/(м·с2) | ,
кг/(м·с2) | ||
7. Вычислите абсолютную и относительную погрешности измерений. Результаты эксперимента сравните с табличным значением.
Задание 2. Определение модуля сдвига методом растяжения пружины.
1. Снять кронштейн с фотодатчиком. Повесить на пружину груз массой . При помощи линейки заметить расположение нижней плоскости груза .
2. Повесить на пружину груз массой . При помощи линейки заметить расположение нижней плоскости груза .
3. Определить удлинение пружины по формуле .
4. Определить модуль сдвига по формуле , где — сила растягивающая пружину, , — средний радиус пружины.
5. Результаты измерений и вычислений внести в таблицу 2.
Таблица 2.
| № | , м | , м | , кг | , кг | , кг | ,
м | , м | , м | ,
кг/(м·с2) | ,
кг/(м·с2) |
6. Проведите измерения для других масс грузов и .
7. Вычислите абсолютную и относительную погрешности измерений. Результаты эксперимента сравните с табличным значением.
Контрольные вопросы
1. Расскажите о явлении деформации. Приведите примеры.
2. Какие бывают деформации? Чем они отличаются друг от друга?
3. Что называется абсолютной величиной деформации и относительной деформацией для различных видов деформаций?
4. Что называется коэффициентом Пуассона? Его физический смысл?
5. Сформулируйте закон Гука. Связь между какими физическими величинами он дает? Физический смысл коэффициента упругости и модуля упругости?
6. Какие деформации называются упругими? Что называется пределом пропорциональности и пределом прочности? Нарисуйте диаграмму напряжений для какого-нибудь вещества и на нем покажите области, соответствующие пределу пропорциональности, пределу упругости, пределу текучести и пределу прочности.
7. Что называется стрелой прогиба? Почему важно знать эту характеристику материала помимо модуля Юнга?
8. Выведите формулу для расчета потенциальной энергии упругодеформированных тел.
9. Нарисуйте петлю упругого гистерезиса и объясните его.
10. Объясните явление деформации с точки зрения строения молекул.
11. Приведите примеры технического применения явления деформации.
12. Какова связь между коэффициентами поперечного и продольного удлинений.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1) Трофимова Т.И. Курс физики: учебное пособие для инженерно-технических специальностей вузов — М.: Academia, 2006.
2) Александров И.В. и др. Современная физика [Электронный ресурс]: учебное пособие для студентов всех форм обучения, обучающихся по техническим и технологическим направлениям и специальностям — Уфа: УГАТУ, 2008.
3) Гринкруг М.С., Вакулюк А.А. Лабораторный практикум по физике [Электронный ресурс] — СПб: Лань, 2012.
4) Калашников Н. П. Основы физики: учебник для вузов: в 2-х т / Н. П. Калашников, М. А. Смондырев — М.: Дрофа, 2007.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФИЛИАЛ ФГБОУ ВПО «УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
В ГОРОДЕ СТЕРЛИТАМАКЕ
Методические указания
к лабораторной работе по курсу общей физики
раздел: раздел: «Механика. Механические колебания. Статистическая физика и термодинамика»
ЛАБОРАТОРНАЯ РАБОТА № 8
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Что такое модуль сдвига? Определение и примеры
Модуль сдвига определяется как отношение напряжения сдвига к деформации сдвига. Он также известен как модуль жесткости и может обозначаться G или, реже, S или μ . Единицей измерения модуля сдвига в системе СИ является паскаль (Па), но значения обычно выражаются в гигапаскалях (ГПа). В английских единицах измерения модуль сдвига выражается в фунтах на квадратный дюйм (PSI) или в килограммах (тысячах) фунтов на квадратный дюйм (ksi).
- Большое значение модуля сдвига указывает на высокую жесткость твердого тела. Другими словами, для создания деформации требуется большая сила.
- Небольшое значение модуля сдвига указывает на то, что твердое тело является мягким или гибким. Чтобы его деформировать, требуется небольшое усилие.
- Одно определение жидкости — это вещество с нулевым модулем сдвига. Любая сила деформирует его поверхность.
Уравнение модуля сдвига
Модуль сдвига определяется путем измерения деформации твердого тела от приложения силы, параллельной одной поверхности твердого тела, в то время как противоположная сила действует на ее противоположную поверхность и удерживает твердое тело на месте.Думайте о сдвиге как о толкании одной стороны блока с трением как противодействующей силе. Другой пример — попытка отрезать проволоку или волосы тупыми ножницами.
Уравнение для модуля сдвига:
G = τ xy / γ xy = F / A / Δx / l = Fl / AΔx
Где:
- G — модуль сдвига или модуль жесткости
- τ xy — напряжение сдвига
- γ xy — деформация сдвига
- A — площадь, на которую действует сила
- Δx — поперечное смещение
- л — начальная длина
Деформация сдвига равна Δx / l = tan θ или иногда = θ, где θ — угол, образованный деформацией, вызванной приложенной силой.
Пример расчета
Например, найдите модуль сдвига образца при напряжении 4×10 4 Н / м 2 , испытывающем деформацию 5×10 -2 .
G = τ / γ = (4×10 4 Н / м 2 ) / (5×10 -2 ) = 8×10 5 Н / м 2 или 8×10 5 Па = 800 кПа
Изотропные и анизотропные материалы
Некоторые материалы изотропны по отношению к сдвигу, что означает, что деформация в ответ на силу одинакова независимо от ориентации.Другие материалы анизотропны и по-разному реагируют на напряжение или деформацию в зависимости от ориентации. Анизотропные материалы гораздо более восприимчивы к сдвигу по одной оси, чем по другой. Например, рассмотрим поведение деревянного блока и то, как он может реагировать на силу, приложенную параллельно волокну древесины, по сравнению с его реакцией на силу, приложенную перпендикулярно волокну. Рассмотрим, как алмаз реагирует на приложенную силу. Насколько легко кристалл сдвигается, зависит от ориентации силы по отношению к кристаллической решетке.
Влияние температуры и давления
Как и следовало ожидать, реакция материала на приложенную силу изменяется в зависимости от температуры и давления. В металлах модуль сдвига обычно уменьшается с повышением температуры. Жесткость уменьшается с увеличением давления. Для прогнозирования влияния температуры и давления на модуль сдвига используются три модели: модель напряжения пластического течения при механическом пороговом напряжении (MTS), модель модуля сдвига Надаля и Лепоака (NP) и модуль сдвига Стейнберга-Кохрана-Гинана (SCG). модель.Для металлов обычно существует область температуры и давления, в которой изменение модуля сдвига является линейным. Вне этого диапазона моделировать поведение сложнее.
Таблица значений модуля сдвига
Это таблица значений модуля сдвига образца при комнатной температуре. Мягкие, гибкие материалы обычно имеют низкие значения модуля сдвига. Щелочноземельные и основные металлы имеют промежуточные значения. Переходные металлы и сплавы имеют высокие значения. Алмаз, твердое и жесткое вещество, имеет чрезвычайно высокий модуль сдвига.
| Материал | Модуль сдвига (ГПа) |
| Резина | 0,0006 |
| Полиэтилен | 0,117 |
| Фанера | 0,62 |
| Нейлон | 4,1 |
| Свинец (Pb) | 13,1 |
| Магний (Mg) | 16,5 |
| Кадмий (Cd) | 19 |
| Кевлар | 19 |
| Бетон | 21 |
| Алюминий (Al) | 25.5 |
| Стекло | 26,2 |
| Латунь | 40 |
| Титан (Ti) | 41,1 |
| Медь (Cu) | 44,7 |
| Железо (Fe) | 52,5 |
| Сталь | 79,3 |
| Алмаз (C) | 478,0 |
Обратите внимание, что значения модуля Юнга следуют аналогичной тенденции. Модуль Юнга — это мера жесткости твердого тела или линейного сопротивления деформации.Модуль сдвига, модуль Юнга и объемный модуль — это модули упругости, все они основаны на законе Гука и связаны друг с другом уравнениями.
Источники
- Crandall, Dahl, Lardner (1959). Введение в механику твердого тела . Бостон: Макгроу-Хилл. ISBN 0-07-013441-3.
- Guinan, M; Стейнберг, Д. (1974). «Производные по давлению и температуре модуля изотропного поликристаллического сдвига для 65 элементов». Журнал физики и химии твердого тела .35 (11): 1501. doi: 10.1016 / S0022-3697 (74) 80278-7
- Ландау Л.Д., Питаевский Л.П., Косевич А.М., Лифшиц Е.М. (1970). Теория упругости , т. 7. (Теоретическая физика). 3-е изд. Пергамон: Оксфорд. ISBN: 978-0750626330
- Варшни Ю. (1981). «Температурная зависимость упругих постоянных». Физический обзор B . 2 (10): 3952.
Модуль сдвига — обзор
Как обсуждалось ранее, под действием процесса добычи или увеличения нефтеотдачи / нефтеотдачи насыщенность пластового флюида изменяется со временем.Влияние изменения насыщенности на сейсмические свойства можно смоделировать в технико-экономическом обосновании. Уравнение Гассмана (Gassmann, 1951) является хорошим приближением для расчета влияния замещения жидкости на сейсмические свойства с использованием свойств каркаса. Он вычисляет объемный модуль упругости насыщенной флюидом пористой среды с использованием известных объемных модулей твердой матрицы, каркаса и поровой жидкости. Для породы твердая матрица состоит из породообразующих минералов. Рамка относится к образцу скелетной породы, а поровая жидкость может быть газом, нефтью, водой или смесью всех трех.Уравнение Гассмана можно записать как:
(4.1) Ku = Kd + (1 − Kd / Km) 2ϕKf + 1 − ϕKm − KdKm
, где K u — недренированный модуль объемной упругости породы, насыщенной жидкость с модулем объемного сжатия K f , K d — это модуль объемного сжатия каркаса, K м — модуль объемного сжатия матрицы (зерна), а ϕ — пористость (Wang, 2001). Моделирование замещения жидкости с использованием уравнения Гассмана (4.1) включает определение следующих четырех компонентов (Smith et al., 2003): (1) пористость породы, (2) свойства флюидов (нефти, воды и газа), которые занимают поровое пространство, а именно, модули упругости и плотности, (3) модуль объемной упругости твердых зерен, и (4) модуль объемной упругости сухого каркаса из пористой породы. Как правило, при моделировании замещения жидкости изучается изменение K и с насыщением, которое, в свою очередь, может быть использовано для изучения изменения скоростей продольных и поперечных волн. Если модуль объемной упругости в сухом состоянии / каркасе неизвестен, его можно вычислить, используя обратное уравнение Гассмана, которое обсуждается позже в уравнении (4.5), для чего нужна информация из первых рук (исходная) K u . Первое значение модуля объемной упругости без дренажа можно рассчитать как:
(4.2) Ku = ρbVP2−4 / 3VS2
, где V p , V s и ρ b являются P — скорость волны, скорость поперечной волны и объемная плотность соответственно. Объемная плотность определяется как:
(4.2a) ρb = ϕρf + (1 − ϕ) ρm
, где ρ f и ρ м — смесь флюидов и минеральная плотность твердой породы, соответственно.
Для базового случая значения модельной скорости продольной волны, скорости поперечной волны и плотности извлекаются из данного каротажа скважины. В отсутствие каротажа S-волн значение V с рассчитывается с использованием соотношения для обломочных пород, предложенного Castagna et al. (1985). Эта так называемая линия глинистой породы для скоростей в км / с задается как:
(4.3) Vp = 1,16Vs + 1,36
Когда известен недренированный объемный модуль K u , модуль объемной упругости в сухом состоянии рассчитывается с использованием обратное уравнение Гассмана (Wang, 2001).
(4.5) Kd = KuϕKm / Kf + 1 − ϕ − KmϕKmKf + KuKm − 1 − ϕ
Модуль объемной упругости в сухом состоянии K d и модуль сдвига остаются постоянными во время замены жидкости, а новые значения Модуль недренированной объемной упругости для различных значений насыщенности, представляющих мониторы, вычисляется с использованием уравнения Гассмана (4.1). Это уравнение является наиболее популярным уравнением, используемым для моделирования замещения жидкости; однако основные допущения этого уравнения следующие:
- 1.
Порода (как матрица, так и каркас) макроскопически однородна.
- 2.
Поры связаны между собой или сообщаются.
- 3.
Поры заполнены жидкостью без трения.
- 4.
Исследуемая система порода-флюид закрытая (недренированная).
- 5.
Поровая жидкость не взаимодействует с твердым телом таким образом, чтобы смягчить или упрочнить каркас.
Уравнение Гассмана не дает надежных результатов, когда нарушаются основные допущения относительно частоты или связности пор, как в случае сланцевых песков или карбонатных пород.
Чтобы выполнить моделирование замещения флюидов с использованием уравнения Гассмана (4.1), мы должны сначала определить: (1) пористость породы, (2) свойства флюидов, которые занимают поровое пространство, и (3) и объем модуль минеральной матрицы ( К м ). Все три компонента могут быть определены или выведены путем лабораторных измерений или анализа данных каротажа на кабеле.
Формула модуля сдвига | Пример и практический вопрос
Пусть при приложении силы F по касательной к верхней поверхности коробки, закрепленной снизу, верхняя поверхность смещается на x, а плоскость, перпендикулярная силе, поворачивается на угол \ [ \ theta \], как показано.
Затем напряжение сдвига: \ [\ sigma = \ frac {F} {A} \]
Деформация сдвига: \ [\ theta = \ frac {x} {L} \] (Как \ [\ theta \] очень и очень мало, \ [\ tan \ theta = \ theta \])
L — перпендикулярное расстояние (в плоскости, перпендикулярной силе) до слоя, который смещается на величину x от фиксированного слой.
Тогда модуль сдвига: \ [G = \ frac {{shear \, \, \, stress}} {{shear \, \, \, stretch}} = \ frac {{F / A}} {{x / L}} = \ frac {{FL}} {{Ax}} \]
Единица модуля сдвига — Нм –2 или паскаль (Па).
Пример 1
Тонкая квадратная пластина размерами 80 см × 80 см × 0,5 см закреплена вертикально на одной из ее меньших поверхностей. Сверху на него действует сила сдвига 2,8 × 104 Н. Верхняя грань куба смещена на 0,16 мм относительно нижней поверхности. Найдите модуль упругости материала пластины при сдвиге.
Решение:
Ситуация показана на рисунке.
F = 2.{10}} Па \]
Практический вопрос
О приложении усилия сдвига 8 кН к кубу с ребром 4 см, изготовленному из материала с модулем сдвига 2 × 10 9 Па, верхняя грань куба смещается на:
(a) 0,1 мм (b) 0,1 см (c) 0,4 мм (d) 0,2 см
Ans (a)
| Формулы преобразования — редактировать | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Упругие свойства однородных изотропных линейных упругих материалов однозначно определяются любыми двумя модулями.{2}}}} | |||||||||||
| (VP, VS) {\ displaystyle (V _ {\ mathrm {P}}, \, V _ {\ mathrm {S}})} | (μ, λ) {\ Displaystyle (\ му, \, \ лямбда)} | (E, λ) † {\ displaystyle (E, \, \ lambda) \, \ dagger} | (Е, μ) {\ Displaystyle (Е, \, \ му)} | (К, λ) {\ Displaystyle (К, \, \ лямбда)} | (К, μ) {\ Displaystyle (К, \, \ му)} | (К, Е) {\ Displaystyle (К, \, E)} | (ν, λ) {\ Displaystyle (\ ню, \, \ лямбда)} | (ν, μ) {\ Displaystyle (\ ню, \, \ му)} | (ν, E) {\ Displaystyle (\ Nu, \, E)} | (ν, К) {\ Displaystyle (\ ню, \, К)} | |
| Скорость P-волны VP = {\ displaystyle V _ {\ mathrm {P}} = \,} | VP {\ displaystyle V _ {\ mathrm {P}}} | λ + 2μρ {\ displaystyle {\ sqrt {\ tfrac {\ lambda +2 \ mu} {\ rho}}}} | E − λ + X2ρ {\ displaystyle {\ sqrt {\ tfrac {E- \ lambda + X} {2 \ rho}}}}} | μ (E − 4μ) ρ (E − 3μ) {\ Displaystyle {\ sqrt {\ tfrac {\ mu \, (E-4 \ mu)} {\ rho \, (E-3 \ mu)}}} } | 3K − 2λρ {\ displaystyle {\ sqrt {\ tfrac {3K-2 \ lambda} {\ rho}}}} | K + 43μρ {\ displaystyle {\ sqrt {\ tfrac {K + {\ frac {4} {3}} \ mu} {\ rho}}}} | 3K (3K + E) ρ (9K − E) {\ displaystyle {\ sqrt {\ tfrac {3K \ left (3K + E \ right)} {\ rho \ left (9K-E \ right)}}}} | λ (1 − ν) ρν {\ Displaystyle {\ sqrt {\ tfrac {\ lambda (1- \ nu)} {\ rho \ nu}}}} | 2μ (1 − ν) ρ (1-2ν) {\ Displaystyle {\ sqrt {\ tfrac {2 \ mu (1- \ nu)} {\ rho (1-2 \ nu)}}}} | E (1 − ν) ρ (1 + ν) (1-2ν) {\ displaystyle {\ sqrt {\ tfrac {E (1- \ nu)} {\ rho (1+ \ nu) (1-2 \ ню)}}}} | 3K (1 − ν) ρ (1 + ν) {\ Displaystyle {\ sqrt {\ tfrac {3K (1- \ nu)} {\ rho (1+ \ nu)}}}} |
| Скорость S-волны VS = {\ displaystyle V _ {\ mathrm {S}} = \,} | VS {\ displaystyle V _ {\ mathrm {S}}} | мкр {\ displaystyle {\ sqrt {\ tfrac {\ mu} {\ rho}}}} | E − 3λ + X4ρ {\ displaystyle {\ sqrt {\ tfrac {E-3 \ lambda + X} {4 \ rho}}}} | мкр {\ displaystyle {\ sqrt {\ tfrac {\ mu} {\ rho}}}} | 3 (K − λ) 2ρ {\ Displaystyle {\ sqrt {\ tfrac {3 (K- \ lambda)} {2 \ rho}}}} | мкр {\ displaystyle {\ sqrt {\ tfrac {\ mu} {\ rho}}}} | −3EKρ (E − 9K) {\ displaystyle {\ sqrt {- {\ tfrac {3EK} {\ rho \ left (E-9K \ right)}}}}} | λ2νρ − λρ {\ displaystyle {\ sqrt {{\ tfrac {\ lambda} {2 \ nu \ rho}} — {\ tfrac {\ lambda} {\ rho}}}}} | мкр {\ displaystyle {\ sqrt {\ tfrac {\ mu} {\ rho}}}} | E2ρ (1 + ν) {\ displaystyle {\ sqrt {\ tfrac {E} {2 \ rho (1+ \ nu)}}}} | −3K (2ν − 1) 2ρ (ν + 1) {\ displaystyle {\ sqrt {- {\ tfrac {3K (2 \ nu -1)} {2 \ rho (\ nu +1)}}}}} |
| Соотношение скоростей Γ = {\ displaystyle \ Gamma = \,} | VPVS {\ displaystyle {\ frac {V _ {\ mathrm {P}}} {V _ {\ mathrm {S}}}}} | λ + 2μμ {\ displaystyle {\ sqrt {\ tfrac {\ lambda +2 \ mu} {\ mu}}}} | 3E + 3λ + X2E {\ displaystyle {\ sqrt {\ tfrac {3E + 3 \ lambda + X} {2E}}}} | E − 4μE − 3μ {\ displaystyle {\ sqrt {\ tfrac {E-4 \ mu} {E-3 \ mu}}}} | 43λ − 2Kλ − K {\ displaystyle {\ sqrt {\ tfrac {{\ tfrac {4} {3}} \ lambda -2K} {\ lambda -K}}}} | K + 43μμ {\ displaystyle {\ sqrt {\ tfrac {K + {\ frac {4} {3}} \ mu} {\ mu}}}} | E + 3KE {\ displaystyle {\ sqrt {\ tfrac {E + 3K} {E}}}} | 2ν − 22ν − 1 {\ Displaystyle {\ sqrt {\ tfrac {2 \ nu -2} {2 \ nu -1}}}} | 2ν − 22ν − 1 {\ Displaystyle {\ sqrt {\ tfrac {2 \ nu -2} {2 \ nu -1}}}} | 2ν − 22ν − 1 {\ Displaystyle {\ sqrt {\ tfrac {2 \ nu -2} {2 \ nu -1}}}} | 2ν − 22ν − 1 {\ Displaystyle {\ sqrt {\ tfrac {2 \ nu -2} {2 \ nu -1}}}} |
| 1-й параметр Ламе λ = {\ displaystyle \ lambda = \,} | ρ (VP2−2VS2) {\ Displaystyle \ rho (V _ {\ mathrm {P}} ^ {2} -2V _ {\ mathrm {S}} ^ {2})} | λ {\ Displaystyle \ лямбда} | λ {\ Displaystyle \ лямбда} | μ (E − 2μ) 3μ − E {\ displaystyle {\ tfrac {\ mu (E-2 \ mu)} {3 \ mu -E}}} | λ {\ Displaystyle \ лямбда} | К − 2μ3 {\ Displaystyle К — {\ tfrac {2 \ mu} {3}}} | 3K (3K-E) 9K-E {\ displaystyle {\ tfrac {3K (3K-E)} {9K-E}}} | λ {\ Displaystyle \ лямбда} | 2μν1−2ν {\ displaystyle {\ tfrac {2 \ mu \ nu} {1-2 \ nu}}} | Eν (1 + ν) (1-2ν) {\ displaystyle {\ tfrac {E \ nu} {(1+ \ nu) (1-2 \ nu)}}} | 3Kν1 + ν {\ Displaystyle {\ tfrac {3K \ nu} {1+ \ nu}}} |
| Модуль сдвига μ = {\ displaystyle \ mu = \,} | ρVS2 {\ Displaystyle \ rho V _ {\ mathrm {S}} ^ {2}} | мк {\ displaystyle \ mu} | E − 3λ + X4 {\ displaystyle {\ tfrac {E-3 \ lambda + X} {4}}} | мк {\ displaystyle \ mu} | 3 (К − λ) 2 {\ Displaystyle {\ tfrac {3 (K- \ lambda)} {2}}} | мк {\ displaystyle \ mu} | 3KE9K-E {\ displaystyle {\ tfrac {3KE} {9K-E}}} | λ (1-2ν) 2ν {\ Displaystyle {\ tfrac {\ lambda (1-2 \ nu)} {2 \ nu}}} | мк {\ displaystyle \ mu} | E2 (1 + ν) {\ displaystyle {\ tfrac {E} {2 (1+ \ nu)}}} | 3K (1−2ν) 2 (1 + ν) {\ displaystyle {\ tfrac {3K (1-2 \ nu)} {2 (1+ \ nu)}}} |
| Модуль Юнга E = {\ displaystyle E = \,} | ρVS2 (3VP2−4VS2) VP2 − VS2 {\ displaystyle {\ tfrac {\ rho V _ {\ mathrm {S}} ^ {2} (3V _ {\ mathrm {P}} ^ {2} -4V _ {\ mathrm { S}} ^ {2})} {V _ {\ mathrm {P}} ^ {2} -V _ {\ mathrm {S}} ^ {2}}}} | μ (3λ + 2μ) λ + μ {\ displaystyle {\ tfrac {\ mu (3 \ lambda +2 \ mu)} {\ lambda + \ mu}}} | E {\ displaystyle E \} | E {\ displaystyle E} | 9K (K − λ) 3K − λ {\ displaystyle {\ tfrac {9K (K- \ lambda)} {3K- \ lambda}}} | 9Kμ3K + μ {\ displaystyle {\ tfrac {9K \ mu} {3K + \ mu}}} | E {\ displaystyle E \} | λ (1 + ν) (1-2ν) ν {\ Displaystyle {\ tfrac {\ lambda (1+ \ nu) (1-2 \ nu)} {\ nu}}} | 2μ (1 + ν) {\ Displaystyle 2 \ му (1+ \ ню) \,} | E {\ displaystyle E \} | 3K (1-2ν) {\ Displaystyle 3K (1-2 \ nu) \,} |
| Объемный модуль K = {\ displaystyle K = \,} | ρ (VP2−43VS2) {\ displaystyle \ rho (V _ {\ mathrm {P}} ^ {2} — {\ tfrac {4} {3}} V _ {\ mathrm {S}} ^ {2})} | λ + 2μ3 {\ displaystyle \ lambda + {\ tfrac {2 \ mu} {3}}} | E + 3λ + X6 {\ displaystyle {\ tfrac {E + 3 \ lambda + X} {6}}} | Eμ3 (3μ − E) {\ Displaystyle {\ tfrac {E \ mu} {3 (3 \ mu -E)}}} | К {\ displaystyle K} | К {\ displaystyle K} | К {\ displaystyle K} | λ (1 + ν) 3ν {\ displaystyle {\ tfrac {\ lambda (1+ \ nu)} {3 \ nu}}} | 2μ (1 + ν) 3 (1-2ν) {\ displaystyle {\ tfrac {2 \ mu (1+ \ nu)} {3 (1-2 \ nu)}}} | E3 (1-2ν) {\ displaystyle {\ tfrac {E} {3 (1-2 \ nu)}}} | К {\ displaystyle K} |
| Коэффициент Пуассона ν = {\ displaystyle \ nu = \,} | VP2−2VS22 (VP2 − VS2) {\ displaystyle {\ tfrac {V _ {\ mathrm {P}} ^ {2} -2V _ {\ mathrm {S}} ^ {2}} {2 (V _ {\ mathrm { P}} ^ {2} -V _ {\ mathrm {S}} ^ {2})}}} | λ2 (λ + μ) {\ Displaystyle {\ tfrac {\ lambda} {2 (\ lambda + \ mu)}}} | −E − λ + X4λ {\ Displaystyle {\ tfrac {-E- \ lambda + X} {4 \ lambda}}} | E2μ − 1 {\ Displaystyle {\ tfrac {E} {2 \ mu}} — 1} | λ3K − λ {\ Displaystyle {\ tfrac {\ lambda} {3K- \ lambda}}} | 3K − 2μ2 (3K + μ) {\ displaystyle {\ tfrac {3K-2 \ mu} {2 (3K + \ mu)}}} | 3K-E6K {\ displaystyle {\ tfrac {3K-E} {6K}}} | ν {\ Displaystyle \ Nu} | ν {\ Displaystyle \ Nu} | ν {\ Displaystyle \ Nu} | ν {\ Displaystyle \ Nu} |
| Модуль упругости P-волны M = {\ displaystyle M = \,} | ρVP2 {\ displaystyle \ rho V _ {\ mathrm {P}} ^ {2}} | λ + 2μ {\ Displaystyle \ лямбда +2 \ му \,} | E − λ + X2 {\ Displaystyle {\ tfrac {E- \ lambda + X} {2}}} | μ (4μ − E) 3μ − E {\ displaystyle {\ tfrac {\ mu (4 \ mu -E)} {3 \ mu -E}}} | 3K − 2λ {\ Displaystyle 3K-2 \ lambda \,} | К + 4μ3 {\ displaystyle K + {\ tfrac {4 \ mu} {3}}} | 3K (3K + E) 9K − E {\ displaystyle {\ tfrac {3K (3K + E)} {9K-E}}} | λ (1 − ν) ν {\ Displaystyle {\ tfrac {\ lambda (1- \ nu)} {\ nu}}} | 2μ (1 − ν) 1−2ν {\ displaystyle {\ tfrac {2 \ mu (1- \ nu)} {1-2 \ nu}}} | E (1 − ν) (1 + ν) (1−2ν) {\ displaystyle {\ tfrac {E (1- \ nu)} {(1+ \ nu) (1-2 \ nu)}}} | 3K (1 − ν) 1 + ν {\ displaystyle {\ tfrac {3K (1- \ nu)} {1+ \ nu}}} |
Напряжение, деформация и модуль Юнга
Напряжение
Напряжение — это отношение приложенной силы F к площади поперечного сечения — , определяемой как « силы на единицу площади ».
- растягивающее напряжение — напряжение, которое имеет тенденцию к растяжению или удлинению материала — действует нормально по отношению к напряженной области
- сжимающее напряжение — напряжение, которое имеет тенденцию к сжатию или укорачиванию материала — действует нормально по отношению к напряженной области
- напряжение сдвига — напряжение, которое имеет тенденцию к сдвигу материала — действует в плоскости напряженной области под прямым углом к напряжению сжатия или растяжения
Напряжение растяжения или сжатия — нормальное напряжение
Напряжение растяжения или сжатия перпендикулярно плоскости обычно обозначается как « нормальное напряжение » или « прямое напряжение » и может быть выражено как
σ = F n / A (1)
где
σ = нормальное напряжение (Па (Н / м 2 ), фунт / кв. дюйм (фунт f / дюйм 2 ))
F n = нормальная сила, действующая перпендикулярно площади (Н, фунт f )
A = площадь (м 2 , дюйм 2 )
- кип — британская система мер единица силы — равна 1000 фунтов f (фунт-сила)
- 1 кип = 4448.2216 Ньютонов (Н) = 4.4482216 килограммов Ньютонов (кН)
Нормальная сила действует перпендикулярно площади и возникает всякий раз, когда внешние нагрузки имеют тенденцию толкать или тянуть два сегмента тела.
Пример — Растягивающая сила, действующая на стержень
Сила 10 кН действует на круглый стержень диаметром 10 мм . Напряжение в стержне можно рассчитать как
σ = (10 10 3 Н) / (π ((10 10 -3 м) / 2) 2 )
= 127388535 (Н / м 2 )
= 127 (МПа)
Пример — Сила, действующая на квадратную стойку из пихты Дугласа
Сжимающая нагрузка 30000 фунтов действует на короткий квадрат 6 x 6 дюймов столб из пихты Дугласа.Размер стойки в оправе составляет 5,5 x 5,5 дюйма , а напряжение сжатия можно рассчитать как
σ = (30000 фунтов) / ((5,5 дюйма) (5,5 дюйма) )
= 991 (фунт / дюйм 2 , фунт / кв. дюйм)
Напряжение сдвига
Напряжение, параллельное плоскости, обычно обозначается как «напряжение сдвига » и может быть выражено как
τ = F p / A (2)
где
τ = напряжение сдвига (Па (Н / м 2 ), фунт / кв. Дюйм (фунт f / дюйм 2 ))
F p = поперечная сила в плоскости области (Н, фунт f )
A = площадь (м 2 , в 2 )
Поперечная сила лежит в плоскости области и возникает, когда внешние нагрузки имеют тенденцию вызывать два сегмента тела скользить друг по другу.
Деформация (деформация)
Деформация определяется как «деформация твердого тела под действием напряжения».
- Нормальная деформация — удлинение или сжатие отрезка линии
- Деформация сдвига — изменение угла между двумя отрезками прямой, первоначально перпендикулярными
Нормальная деформация и может быть выражена как
ε = дл / л o
= σ / E (3)
, где
dl = изменение длины (м, дюйм)
l o = начальная длина (м, дюйм)
ε = деформация — без единицы измерения
E = Модуль Юнга (модуль упругости) (Па, (Н / м 2 ), фунт / кв. дюйм (фунт f / дюйм 2 ))
- Модуль Юнга можно использовать для прогнозирования удлинения или сжатия объекта при воздействии силы.
Обратите внимание, что деформация является безразмерной единицей, поскольку это отношение двух длин.Но также общепринято указывать это как отношение двух единиц длины — например, м / м или дюйм / дюйм .
Пример — напряжение и изменение длины
Стержень в приведенном выше примере имеет длину 2 м и изготовлен из стали с модулем упругости 200 ГПа (200 10 9 Н / м 2 ) . Изменение длины можно рассчитать, преобразовав (3) в
dl = σ l o / E
= (127 10 6 Па) (2 м) / (200 10 9 Па)
= 0.00127 м
= 1,27 мм
Энергия деформации
Напряжение объекта сохраняет в нем энергию. Для осевой нагрузки запасенная энергия может быть выражена как
U = 1/2 F n dl
, где
U = энергия деформации (Дж (Н · м), фут-фунт)
Модуль Юнга — модуль упругости (или модуль упругости при растяжении) — закон Гука
Большинство металлов деформируются пропорционально приложенной нагрузке в диапазоне нагрузок.Напряжение пропорционально нагрузке, а деформация пропорциональна деформации в соответствии с законом Гука .
E = напряжение / деформация
= σ / ε
= (F n / A) / (дл / л o ) ( 4)
, где
E = модуль Юнга (Н / м 2 ) (фунт / дюйм 2 , psi)
Модуль упругости или модуль Юнга обычно используется для металлов и металлических сплавов и выражается в единицах 10 6 фунтов f / дюйм 2 , Н / м 2 или Па .Модуль упругости при растяжении часто используется для пластмасс и выражается в терминах 10 5 фунтов f / дюйм 2 или ГПа .
Модуль упругости при сдвиге — или модуль жесткости
G = напряжение / деформация
= τ / γ
= (F p / A) / (с / d) (5)
, где
G = модуль упругости при сдвиге — или модуль жесткости (Н / м 2 ) (фунт / дюйм 2 , psi)
τ = напряжение сдвига ((Па) Н / м 2 , psi)
γ = мера деформации сдвига без единицы измерения
7
7 p = сила, параллельная граням, на которые они действуют
A = площадь (м 2 , в 2 )
s = смещение граней (м, дюйм)
d = ди положение между смещенными гранями (м, дюйм)
Объемный модуль упругости
Объемный модуль упругости — или объемный модуль — является мерой сопротивления вещества равномерному сжатию.Объемный модуль упругости — это отношение напряжения к изменению объема материала, подвергающегося осевой нагрузке.
Модули упругости
Модули упругости для некоторых распространенных материалов:
| Материал | Модуль упругости — E — | Модуль упругости при сдвиге — G — | Модуль упругости — 9046 |
|---|---|---|---|
| (ГПа) (10 6 фунтов на кв. Дюйм) | (ГПа) (10 6 фунтов на кв. Дюйм) | (ГПа) 600058 9005 ) | |
| Алюминий | 70 | 24 | 70 |
| Латунь | 91 | 36 | 61 |
| Медь | 110 | 42 | 140 |
| 55 | 23 | 37 | |
| Железо | 91 | 70 | 100 | Свинец | 16 | 5.6 | 7,7 |
| Сталь | 200 | 84 | 160 |
12.3 Напряжение, деформация и модуль упругости — Университетская физика, Том 1
Цели обучения
К концу этого раздела вы сможет:
- Объяснить концепции напряжения и деформации при описании упругих деформаций материалов
- Описать виды упругого деформирования предметов и материалов
Модель твердого тела — идеализированный пример объекта, не деформирующегося под действием внешних сил.Это очень полезно при анализе механических систем, а многие физические объекты действительно в значительной степени жесткие. Степень, в которой объект может восприниматься как жесткий, зависит от физических свойств материала, из которого он сделан. Например, мяч для пинг-понга, сделанный из пластика, является хрупким, а теннисный мяч, сделанный из резины, эластичным, когда на него воздействуют сжимающие силы. Однако при других обстоятельствах и мяч для пинг-понга, и теннисный мяч могут хорошо отскакивать как твердые тела.Точно так же тот, кто проектирует протезы конечностей, может приблизиться к механике человеческих конечностей, моделируя их как твердые тела; однако фактическая комбинация костей и тканей представляет собой эластичную среду.
В оставшейся части этой главы мы переходим от рассмотрения сил, влияющих на движение объекта, к тем, которые влияют на форму объекта. Изменение формы из-за приложения силы называется деформацией. Известно, что даже очень небольшие силы вызывают некоторую деформацию.Деформация испытывается объектами или физическими средами под действием внешних сил — например, это может быть сжатие, сжатие, разрыв, скручивание, срезание или растяжение объектов. На языке физики два термина описывают силы, действующие на деформируемые объекты: напряжение и напряжение .
Напряжение — это величина, которая описывает величину сил, вызывающих деформацию. Напряжение обычно определяется как сила на единицу площади .Когда силы притягивают объект и вызывают его удлинение, например, при растяжении эластичной ленты, мы называем такое напряжение растягивающим напряжением. Когда силы вызывают сжатие объекта, мы называем это напряжением сжатия. Когда объект сдавливается со всех сторон, как подводная лодка в глубинах океана, мы называем этот вид напряжения объемным напряжением (или объемным напряжением). В других ситуациях действующие силы могут быть ни растягивающими, ни сжимающими, и все же вызывать заметную деформацию. Например, предположим, что вы крепко держите книгу ладонями, затем одной рукой вы нажимаете и тянете переднюю обложку от себя, а другой рукой вы нажимаете и тянете заднюю обложку в направлении ты.В таком случае, когда деформирующие силы действуют по касательной к поверхности объекта, мы называем их «поперечными» силами, а вызываемое ими напряжение — поперечным напряжением.
Единицей измерения напряжения в системе СИ является паскаль (Па). Когда сила в один ньютон воздействует на единицу площади квадратного метра, результирующее напряжение составляет один паскаль:
один паскаль = 1.0Па = 1.0N1.0м2. один паскаль = 1.0Па = 1.0N1.0м2.
В британской системе единиц единицей измерения напряжения является «фунт / кв. Дюйм», что означает «фунт на квадратный дюйм» (фунт / дюйм2).(фунт / дюйм2). Другой единицей измерения объемного напряжения является атм (атмосфера). Коэффициенты пересчета:
1 фунт / кв. Дюйм = 6895 Па и 1 Па = 1,450 × 10–4 фунт / кв. Дюйм · атм = 1,013 × 105 Па = 14,7 фунт / кв. Дюйм. 1 фунт / кв. Дюйм = 6895 Па и 1 Па = 1,450 × 10–4 фунт / кв.
Объект или среда под напряжением деформируются. Величина, описывающая эту деформацию, называется деформацией. Деформация задается как частичное изменение длины (при растягивающем напряжении), объема (при объемном напряжении) или геометрии (при напряжении сдвига). Следовательно, деформация — это безразмерное число.Деформация под действием растягивающего напряжения называется деформацией растяжения, деформация под действием объемного напряжения называется объемной деформацией (или объемной деформацией), а деформация, вызванная напряжением сдвига, называется деформацией сдвига.
Чем больше напряжение, тем больше напряжение; однако связь между деформацией и напряжением не обязательно должна быть линейной. Только когда напряжение достаточно низкое, деформация, которую оно вызывает, прямо пропорциональна величине напряжения. Константа пропорциональности в этом отношении называется модулем упругости.В линейном пределе низких значений напряжения общее соотношение между напряжением и деформацией составляет
напряжение = (модуль упругости) × деформация. напряжение = (модуль упругости) × деформация.
12,33
Как видно из анализа размеров этого соотношения, модуль упругости имеет ту же физическую единицу, что и напряжение, поскольку деформация безразмерна.
Из уравнения 12.33 также видно, что, когда объект характеризуется большим значением модуля упругости, влияние напряжения невелико. С другой стороны, небольшой модуль упругости означает, что напряжение вызывает большую деформацию и заметную деформацию.Например, напряжение на резиновой ленте вызывает большую деформацию (деформацию), чем такое же напряжение на стальной ленте тех же размеров, потому что модуль упругости резины на два порядка меньше модуля упругости стали.
Модуль упругости для растягивающего напряжения называется модулем Юнга; то, что для объемного напряжения называется объемным модулем упругости; а напряжение сдвига называется модулем сдвига. Обратите внимание, что соотношение между напряжением и деформацией — это наблюдаемое соотношение , измеренное в лаборатории.Модули упругости для различных материалов измеряются при различных физических условиях, таких как изменяющаяся температура, и собираются в таблицах технических данных для справки (таблица 12.1). Эти таблицы являются ценными справочными материалами для промышленности и для всех, кто занимается проектированием или строительством. В следующем разделе мы обсудим отношения между деформацией и напряжением за пределами линейного предела, представленного уравнением 12.33, в полном диапазоне значений напряжения до точки разрушения. В оставшейся части этого раздела мы изучаем линейный предел, выражаемый уравнением 12.33.
| Материал | Модуль Юнга × 1010 Па × 1010 Па | Объемный модуль × 1010 Па × 1010 Па | Модуль сдвига × 1010 Па × 1010 Па |
|---|---|---|---|
| Алюминий | 7,0 | 7,5 | 2,5 |
| Кость (напряжение) | 1,6 | 0,8 | 8,0 |
| Кость (компрессия) | 0,9 | ||
| Латунь | 9.0 | 6,0 | 3,5 |
| Кирпич | 1,5 | ||
| Бетон | 2,0 | ||
| Медь | 11,0 | 14,0 | 4,4 |
| Коронное стекло | 6,0 | 5,0 | 2,5 |
| Гранит | 4,5 | 4,5 | 2,0 |
| Волосы (человеческие) | 1.0 | ||
| Твердая древесина | 1,5 | 1,0 | |
| Утюг | 21,0 | 16,0 | 7,7 |
| Свинец | 1,6 | 4,1 | 0,6 |
| Мрамор | 6,0 | 7,0 | 2,0 |
| Никель | 21,0 | 17,0 | 7,8 |
| Полистирол | 3.0 | ||
| Шелк | 6,0 | ||
| Паутинка | 3,0 | ||
| Сталь | 20,0 | 16,0 | 7,5 |
| Ацетон | 0,07 | ||
| Этанол | 0,09 | ||
| Глицерин | 0.45 | ||
| Меркурий | 2,5 | ||
| Вода | 0,22 |
Таблица 12.1 Приблизительные модули упругости для выбранных материалов
Напряжение при растяжении или сжатии, деформация и модуль Юнга
Напряжение или сжатие возникает, когда две антипараллельные силы равной величины действуют на объект только вдоль одного из его измерений таким образом, что объект не перемещается.Один из способов представить себе такую ситуацию показан на рисунке 12.18. Сегмент стержня либо растягивается, либо сжимается парой сил, действующих по его длине и перпендикулярно его поперечному сечению. Чистый эффект таких сил состоит в том, что стержень изменяет свою длину от исходной длины L0L0, которая была у него до появления сил, на новую длину L , которую он имеет под действием сил. Это изменение длины ΔL = L-L0ΔL = L-L0 может быть либо удлинением (когда L больше исходной длины L0) L0), либо сокращением (когда L меньше исходной длины L0).L0). Напряжение растяжения и деформация возникают, когда силы растягивают объект, вызывая его удлинение, и изменение длины ΔLΔL является положительным. Напряжение сжатия и деформация возникают, когда силы сжимают объект, вызывая его сокращение, а изменение длины ΔLΔL отрицательно.
В любой из этих ситуаций мы определяем напряжение как отношение деформирующей силы F⊥F⊥ к площади A поперечного сечения деформируемого объекта. Символ F⊥F⊥, который мы оставляем для деформирующей силы, означает, что эта сила действует перпендикулярно поперечному сечению объекта.Силы, действующие параллельно поперечному сечению, не изменяют длину объекта. Определение растягивающего напряжения —
растягивающее напряжение = F⊥A. растягивающее напряжение = F⊥A.
12,34
Деформация растяжения — это мера деформации объекта при растягивающем напряжении и определяется как частичное изменение длины объекта, когда объект испытывает растягивающее напряжение
деформация растяжения = ΔLL0. деформация растяжения = ΔLL0.
12,35
Напряжение сжатия и деформация определяются по той же формуле, уравнение 12.34 и уравнение 12.35 соответственно. Единственное отличие от ситуации с растяжением состоит в том, что для напряжения и деформации сжатия мы берем абсолютные значения правых частей в уравнениях 12.34 и 12.35.
Рис. 12.18. Когда объект находится в состоянии растяжения или сжатия, результирующая сила, действующая на него, равна нулю, но объект деформируется, изменяя свою исходную длину L0.L0. (a) Натяжение: стержень удлинен на ΔL.ΔL. (b) Сжатие: стержень сжимается на ΔL.ΔL. В обоих случаях деформирующая сила действует по длине стержня и перпендикулярно его поперечному сечению.В линейном диапазоне малых напряжений площадь поперечного сечения стержня не изменяется.
Модуль Юнга Y — это модуль упругости, когда деформация вызвана либо растягивающим, либо сжимающим напряжением, и определяется уравнением 12.33. Разделив это уравнение на деформацию растяжения, мы получим выражение для модуля Юнга:
Y = растягивающая деформация растяжения = F⊥ / AΔL / L0 = F⊥AL0ΔL.Y = растягивающая деформация растяжения = F⊥ / AΔL / L0 = F⊥AL0ΔL.
12,36
Пример 12,7
Напряжение сжатия в опоре
Скульптура весом 10 000 Н стоит на горизонтальной поверхности на вершине 6.Вертикальный столб высотой 0 м Рис. 12.19. Площадь поперечного сечения столба 0,20 м 20,20 м 2, он выполнен из гранита с удельной массой 2700 кг / м3. 2700 кг / м3. Найдите сжимающее напряжение в поперечном сечении, расположенном на 3,0 м ниже вершины столба, и значение сжимающей деформации верхнего 3,0-метрового сегмента столба.
Рисунок 12.19 Колонна Нельсона на Трафальгарской площади, Лондон, Англия. (кредит: модификация работы Кристиана Бортеса)
Стратегия
Сначала мы находим вес 3.Верхняя часть столба длиной 0 м. Нормальная сила, действующая на поперечное сечение, расположенное на 3,0 м ниже вершины, складывается из веса столба и веса скульптуры. Когда у нас есть нормальная сила, мы используем уравнение 12.34, чтобы найти напряжение. Чтобы найти деформацию сжатия, мы находим значение модуля Юнга для гранита в таблице 12.1 и инвертируем уравнение 12.36.
Решение
Объем сегмента колонны высотой h = 3,0мh = 3,0м и площадью поперечного сечения A = 0,20м2A = 0,20м2 составляет
V = Ah = (0.20м2) (3,0м) = 0,60м3. V = Ah = (0,20м2) (3,0м) = 0,60м3.
При плотности гранита ρ = 2,7 × 103 кг / м3, ρ = 2,7 × 103 кг / м3 масса сегмента столба составляет
m = ρV = (2,7 × 103 кг / м3) (0,60 м3) = 1,60 × 103 кг. m = ρV = (2,7 × 103 кг / м3) (0,60 м3) = 1,60 × 103 кг.
Вес сегмента стойки
wp = mg = (1,60 × 103 кг) (9,80 м / с2) = 1,568 × 104 Н. wp = mg = (1,60 × 103 кг) (9,80 м / с2) = 1,568 × 104 Н.
Вес скульптуры ws = 1,0 × 104 Н, ws = 1,0 × 104 Н, поэтому нормальная сила на поверхности поперечного сечения, расположенной на 3,0 м ниже скульптуры, составляет
F⊥ = wp + ws = (1.568 + 1.0) × 104N = 2.568 × 104N. F⊥ = wp + ws = (1.568 + 1.0) × 104N = 2.568 × 104N.
Следовательно, напряжение
напряжение = F⊥A = 2,568 × 104N0,20м2 = 1,284 × 105Па = 128,4 кПа. напряжение = F⊥A = 2,568 × 104N0,20м2 = 1,284 × 105Па = 128,4 кПа.
Модуль Юнга для гранита Y = 4,5 × 1010 Па = 4,5 × 107 кПа. Y = 4,5 × 1010 Па = 4,5 × 107 кПа. Следовательно, деформация сжатия в этом положении составляет
деформация = напряжение Y = 128,4 кПа 4,5 × 107 кПа = 2,85 × 10-6. деформация = напряжение Y = 128,4 кПа 4,5 × 107 кПа = 2,85 × 10-6.
Значение
Обратите внимание, что нормальная сила, действующая на площадь поперечного сечения колонны, не является постоянной по всей ее длине, а изменяется от наименьшего значения наверху до наибольшего значения внизу колонны.Таким образом, если опора имеет равномерную площадь поперечного сечения по всей длине, наибольшее напряжение у ее основания.
Проверьте свое понимание 12.9
Найдите сжимающее напряжение и деформацию в основании колонны Нельсона.
Пример 12,8
Растяжка стержня
Стальной стержень длиной 2,0 м имеет площадь поперечного сечения 0,30 см2 0,30 см2. Штанга является частью вертикальной опоры, которая удерживает тяжелую платформу весом 550 кг, которая подвешена к нижнему концу штанги. Пренебрегая весом стержня, каково растягивающее напряжение стержня и удлинение стержня под действием напряжения?
Стратегия
Сначала мы вычисляем растягивающее напряжение в стержне под весом платформы в соответствии с уравнением 12.34. Затем мы инвертируем уравнение 12.36, чтобы найти удлинение стержня, используя L0 = 2,0 м. L0 = 2,0 м. Из таблицы 12.1 модуль Юнга для стали составляет Y = 2,0 × 1011 Па. Y = 2,0 × 1011 Па.
Решение
Подстановка числовых значений в уравнения дает нам
F⊥A = (550 кг) (9,8 м / с2) 3,0 × 10–5 м2 = 1,8 × 108 Па ΔL = F⊥AL0Y = (1,8 × 108 Па) 2,0 м2,0 × 1011 Па = 1,8 × 10–3 м = 1,8 мм.F⊥ A = (550 кг) (9,8 м / с2) 3,0 × 10–5 м2 = 1,8 × 108 Па ΔL = F⊥AL0Y = (1,8 × 108 Па) 2,0 м2,0 × 1011 Па = 1,8 × 10–3 м = 1,8 мм.
Значение
Как и в примере с колонной, растягивающее напряжение в этом примере неоднородно по длине стержня.Однако, в отличие от предыдущего примера, если принять во внимание вес штанги, напряжение в штанге будет наибольшим в верхней части и наименьшим в нижней части штанги, к которой прикреплено оборудование.
Проверьте свое понимание 12.10
Проволока длиной 2,0 м растягивается на 1,0 мм под действием нагрузки. Какова деформация растяжения в проволоке?
Объекты часто могут одновременно испытывать напряжение сжатия и растяжения. Рис. 12.20. Один из примеров — длинная полка, загруженная тяжелыми книгами, которая провисает между концевыми опорами под весом книг.Верхняя поверхность полки испытывает напряжение сжатия, а нижняя поверхность полки — растягивающее напряжение. Точно так же длинные и тяжелые балки провисают под собственным весом. В современном строительстве такие деформации изгиба можно практически исключить с помощью двутавровых балок. Рисунок 12.21.
Рис. 12.20 (a) Объект, изгибающийся вниз, испытывает растягивающее напряжение (растяжение) в верхней части и сжимающее напряжение (сжатие) в нижней части. (b) Элитные тяжелоатлеты часто временно сгибают железные прутья во время подъема, как на Олимпийских играх 2012 года.(кредит б: доработка работы Александра Кочерженко)
Рисунок 12.21 Стальные двутавровые балки используются в строительстве для уменьшения деформаций изгиба. (Источник: модификация работы «Инженерный корпус армии США в Европе» / Flickr)
Объемное напряжение, деформация и модуль
Когда вы ныряете в воду, вы чувствуете силу, давящую на каждую часть вашего тела со всех сторон. Тогда вы испытываете объемный стресс или, другими словами, давление. Объемное напряжение всегда имеет тенденцию к уменьшению объема, заключенного на поверхности погружаемого объекта.Силы этого «сжатия» всегда перпендикулярны погружаемой поверхности. Рис. 12.22. Эффект этих сил заключается в уменьшении объема погруженного объекта на величину ΔVΔV по сравнению с объемом V0V0 объекта при отсутствии объемного напряжения. Этот вид деформации называется объемной деформацией и описывается изменением объема относительно исходного объема:
объемная деформация = ΔVV0. объемная деформация = ΔVV0.
12,37
Рис. 12.22. Объект при увеличении объемного напряжения всегда испытывает уменьшение своего объема.Равные силы, перпендикулярные поверхности, действуют со всех сторон. Эффект этих сил заключается в уменьшении объема на величину ΔVΔV по сравнению с исходным объемом V0.V0.
Объемная деформация возникает в результате объемного напряжения, которое представляет собой силу F⊥F⊥, нормальную к поверхности, которая давит на единицу площади A погруженного объекта. Такая физическая величина, или давление p , определяется как
давление = p≡F⊥A. давление = p≡F⊥A.
12,38
Мы будем изучать давление в жидкостях более подробно в Гидромеханике.Важной характеристикой давления является то, что это скалярная величина, не имеющая определенного направления; то есть давление действует одинаково во всех возможных направлениях. Когда вы погружаете руку в воду, вы чувствуете такое же давление, действующее на верхнюю поверхность руки, как на нижнюю, или на боковую, так и на поверхность кожи между пальцами. В этом случае вы ощущаете увеличение давления ΔpΔp по сравнению с тем, что вы привыкли ощущать, когда ваша рука не погружена в воду.Когда ваша рука не погружена в воду, вы чувствуете нормальное давление p0p0 в одну атмосферу, которое служит точкой отсчета. Объемное напряжение — это увеличение давления, или Δp, Δp, по сравнению с нормальным уровнем, p0.p0.
Когда объемное напряжение увеличивается, объемная деформация увеличивается в соответствии с уравнением 12.33. Константа пропорциональности в этом соотношении называется модулем объемного сжатия, B или
.
B = объемное напряжение, объемная деформация = −ΔpΔV / V0 = −ΔpV0ΔV. B = объемное напряжение, объемная деформация = −ΔpΔV / V0 = −ΔpV0ΔV.
12,39
Знак минус, который появляется в уравнении 12.39, предназначен для согласованности, чтобы гарантировать, что B является положительной величиной. Обратите внимание, что знак минус (-) (-) необходим, потому что увеличение ΔpΔp давления (положительная величина) всегда вызывает уменьшение ΔVΔV в объеме, а уменьшение объема является отрицательной величиной. Величина, обратная модулю объемного сжатия, называется сжимаемостью k, k или
.
k = 1B = −ΔV / V0Δp.k = 1B = −ΔV / V0Δp.
12,40
Термин «сжимаемость» используется в отношении жидкостей (газов и жидкостей).Сжимаемость описывает изменение объема жидкости на единицу увеличения давления. Жидкости, характеризующиеся большой сжимаемостью, относительно легко сжимаются. Например, сжимаемость воды составляет 4,64 × 10–5 / атм. 4,64 × 10–5 / атм, а сжимаемость ацетона составляет 1,45 × 10–4 / атм. 1,45 × 10–4 / атм. Это означает, что при повышении давления на 1,0 атм относительное уменьшение объема для ацетона примерно в три раза больше, чем для воды.
Пример 12.9
Гидравлический пресс
В гидравлическом прессе Рисунок 12.23, 250-литровый объем масла подвергается повышению давления на 2300 фунтов на квадратный дюйм. Если сжимаемость масла составляет 2,0 × 10–5 / атм, 2,0 × 10–5 / атм, найдите объемную деформацию и абсолютное уменьшение объема масла при работе пресса.
Рис. 12.23 В гидравлическом прессе, когда маленький поршень смещается вниз, давление в масле передается через масло на большой поршень, заставляя большой поршень двигаться вверх. Небольшая сила, приложенная к маленькому поршню, вызывает большую силу сжатия, которую большой поршень оказывает на объект, который либо поднимается, либо сжимается.Устройство действует как механический рычаг.
Стратегия
Мы должны обратить уравнение 12.40, чтобы найти объемную деформацию. Во-первых, мы преобразуем увеличение давления из фунтов на квадратный дюйм в атм, Δp = 2300psi = 2300 / 14,7atm≈160atm, Δp = 2300psi = 2300 / 14.7atm≈160atm, и определяем V0 = 250L.V0 = 250L.
Решение
Подставляя значения в уравнение, имеем
объемная деформация = ΔVV0 = ΔpB = kΔp = (2,0 × 10-5 / атм) (160 атм) = 0,0032 ответ: ΔV = 0,0032V0 = 0,0032 (250L) = 0,78L. объемная деформация = ΔVV0 = ΔpB = kΔp = (2,0 × 10-5 / атм) (160атм) = 0,0032 ответ: ΔV = 0.0032V0 = 0,0032 (250 л) = 0,78 л.
Значение
Обратите внимание, что, поскольку сжимаемость воды в 2,32 раза больше, чем у масла, если бы рабочее вещество в гидравлическом прессе этой задачи было заменено на воду, объемная деформация, а также изменение объема были бы в 2,32 раза больше.
Проверьте свое понимание 12.11
Если нормальная сила, действующая на каждую грань кубической стальной детали размером 1,0 м31,0 м3, изменится на 1,0 × 107 Н, 1,0 × 107 Н, найдите результирующее изменение объема куска стали.
Напряжение сдвига, деформация и модуль
Понятия напряжения сдвига и деформации относятся только к твердым объектам или материалам. Здания и тектонические плиты являются примерами объектов, которые могут подвергаться сдвиговым напряжениям. В общем, эти концепции не применимы к жидкостям.
Деформация сдвига возникает, когда две антипараллельные силы равной величины прикладываются по касательной к противоположным поверхностям твердого объекта, не вызывая деформации в поперечном направлении к силовой линии, как в типичном примере напряжения сдвига, показанном на рисунке 12.24. Сдвиговая деформация характеризуется постепенным сдвигом ΔxΔx слоев в направлении, касательном к действующим силам. Эта градация ΔxΔx происходит в поперечном направлении на некотором расстоянии L0.L0. Деформация сдвига определяется отношением наибольшего смещения ΔxΔx к поперечному расстоянию L0L0
деформация сдвига = ΔxL0. деформация сдвига = ΔxL0.
12,41
Деформация сдвига вызвана напряжением сдвига. Напряжение сдвига возникает из-за сил, которые действуют параллельно к поверхности. Для таких сил мы используем символ F∥F forces.Величина F∥F∥ на площадь поверхности A , где применяется сила сдвига, является мерой напряжения сдвига
напряжение сдвига = F∥A. напряжение сдвига = F∥A.
12,42
Модуль сдвига является константой пропорциональности в уравнении 12.33 и определяется отношением напряжения к деформации. Модуль сдвига обычно обозначается S :
.
S = напряжение сдвига деформация сдвига = F∥ / AΔx / L0 = F∥AL0Δx.S = напряжение сдвига деформация сдвига = F∥ / AΔx / L0 = F∥AL0Δx.
12,43
Рис. 12.24. Объект, находящийся под напряжением сдвига: две антипараллельные силы равной величины действуют по касательной к противоположным параллельным поверхностям объекта.Контур пунктирной линией показывает результирующую деформацию. Направление, перпендикулярное действующим силам, не изменяется, и поперечная длина L0L0 не изменяется. Сдвиговая деформация характеризуется постепенным смещением ΔxΔx слоев в направлении, касательном к силам.
Пример 12.10
Старая книжная полка
Уборщик пытается переместить тяжелый старый книжный шкаф по ковровому покрытию, касаясь его поверхности самой верхней полки. Однако единственный заметный эффект от этих усилий аналогичен эффекту, показанному на рисунке 12.24, и он исчезает, когда человек перестает толкать. Книжный шкаф высотой 180 см и шириной 90 см с четырьмя полками глубиной 30 см, частично заполненными книгами. Общий вес книжного шкафа и книг составляет 600,0 Н. Если человек толкает верхнюю полку с силой 50,0 Н, которая смещает верхнюю полку по горизонтали на 15,0 см относительно неподвижной нижней полки, найдите модуль сдвига книжного шкафа.
Стратегия
Единственная важная информация — это физические размеры книжного шкафа, величина тангенциальной силы и смещение, вызываемое этой силой.Мы определяем F∥ = 50.0N, Δx = 15.0cm, F∥ = 50.0N, Δx = 15.0cm, L0 = 180.0cm, L0 = 180.0cm и A = (30.0 cm) (90.0 cm) = 2700.0 cm2, A = (30,0 см) (90,0 см) = 2700,0 см2, и мы используем уравнение 12.43 для вычисления модуля сдвига.
Решение
Подставляя числа в уравнения, получаем для модуля сдвига
S = F∥AL0Δx = 50.0N2700.0cm2180.0cm.15.0cm. = 29Ncm2 = 29 × 104Nm2 = 209 × 103Pa = 2.222 кПа S = F∥AL0Δx = 50.0N2700.0cm2180.0cm.15.0cm. = 29Ncm2 = 29 × 104Нм2 = 209 × 103Па = 2,222 кПа.
Мы также можем найти напряжение сдвига и деформацию соответственно:
F∥A = 50.0N2700,0 см2 = 527 кПа = 185,2 Па ΔxL0 = 15,0 см 180,0 см = 112 = 0,083.F∥A = 50,0N2700,0 см2 = 527 кПа = 185,2 Па ΔxL0 = 15,0 см 180,0 см = 112 = 0,083.
Значение
Если человек в этом примере толкнет полку здоровым движением, может случиться так, что индуцированный сдвиг превратит ее в груду мусора. Примерно тот же механизм сдвига ответственен за разрушения засыпанных землей дамб и дамб; и в целом по оползням.
Проверьте свое понимание 12.12
Объясните, почему концепции модуля Юнга и модуля сдвига неприменимы к жидкостям.
Elasticity — The Physics Hypertextbook
Обсуждение
основы
Эластичность — это свойство твердых материалов возвращаться к своей первоначальной форме и размеру после устранения деформирующих их сил. Вспомните закон Гука — впервые официально сформулированный Робертом Гуком в Истинная теория упругости или упругости (1676)…
uttensio, sic vis
, что буквально можно перевести как…
Как расширение, так и сила.
или официально переведен на…
Вытягивание прямо пропорционально силе.
Скорее всего, мы заменим слово «расширение» на символ (∆ x ), «сила» на символ ( F ), а «прямо пропорционально» на знак равенства (=) и константа пропорциональности ( k ), тогда, чтобы показать, что упругий объект пытается вернуться в исходное состояние, мы добавили бы знак минус (-). Другими словами, мы бы записали уравнение…
F = — k ∆ x
Это закон Гука для пружины — простого объекта, который по сути одномерный.Закон Гука можно обобщить до…
Напряжение пропорционально деформации.
, где деформация относится к изменению некоторого пространственного измерения (длины, угла или объема) по сравнению с его исходным значением, а напряжение относится к причине изменения (сила, приложенная к поверхности).
Коэффициент, который связывает конкретный тип напряжения с возникающей деформацией, называется модулем упругости (множественное число, модули). Модули упругости — это свойства материалов, а не объектов.Есть три основных типа напряжения и три связанных модуля.
| модуль (символы) | напряжение (символ) | штамм (символ) | конфигурация изменить |
|---|---|---|---|
| Янга ( E или Y ) | по нормали к противоположным граням (σ) | длина ε = ∆ℓ / ℓ 0 | длиннее и тоньше или короче и толще |
| ножницы ( G или S ) | по касательной к противоположным граням (τ) | касательная γ = ∆ x / y | прямоугольников превращаются в параллелограммов |
| навалом ( K или B ) | нормально ко всем сторонам, давление ( P ) | объем θ = ∆ V / V 0 | объем изменяется но форма не |
Международные стандартные символы для модулей являются производными от соответствующих неанглийских слов — E для élasticité (французское слово «эластичность»), G для glissement (французский язык для скольжения) и K для компрессии. (нем. Сжатие).Некоторые американские учебники решили порвать с традициями и использовать первую букву каждого модуля на английском языке — Y для Юнга, S для сдвига и B для пухлости.
Напряжения в твердых телах всегда описываются как сила, деленная на площадь. Направление сил может измениться, а единицы — нет. Единица измерения напряжения в системе СИ — ньютон на квадратный метр , которому присвоено особое название паскаль в честь Блеза Паскаля (1623–1662), французского математика (треугольник Паскаля), физика (принцип Паскаля), изобретателя (принцип Паскаля). калькулятор) и философ (пари Паскаля).
| ⎡ ⎢ ⎣ | Па = | N | ⎤ ⎥ |
| м 2 |
Штаммы всегда безразмерны.
| вид штамма | наименование символа | определение | шт. |
|---|---|---|---|
| линейный | эпсилон | ε = ∆ℓ / ℓ 0 | м / м = 1 |
| ножницы | гамма | γ = ∆ x / y | м / м = 1 |
| объем | тета | θ = ∆ V / V 0 | м 3 / м 3 = 1 |
Это означает, что паскаль также является единицей СИ для всех трех модулей.
| напряжение | = | модуль | × | штамм | ||
| [ | Па | = | Па | × | 1 | ] |
отказ — вариант
- Предел упругости, предел текучести
- предел прочности, предел прочности
- Прочность материала — это мера его способности выдерживать нагрузку без разрушения.
- Banerjee, et al. показывают, что когда иглы из монокристаллического алмаза в нанометровом масштабе упруго деформируются, они выходят из строя при максимальной локальной прочности на разрыв от ~ 89 до 98 ГПа.
- Экспериментальные результаты и расчеты ab initio показывают, что модуль упругости углеродных нанотрубок и графена приблизительно равен 1 ТПа.
- Напротив, заявленная прочность на разрыв объемного кубического алмаза составляет <10 ГПа
Модуль Юнга
Представьте себе кусок теста.Растяните это. Он становится длиннее и тоньше. Раздавите это. Он становится короче и толще. А теперь представьте кусок гранита. Проведите тот же мысленный эксперимент. Изменение формы обязательно должно произойти, но невооруженным глазом незаметно. Некоторые материалы довольно легко растягиваются и сжимаются. Некоторые этого не делают.
Величина, которая описывает реакцию материала на напряжения, приложенные перпендикулярно противоположным граням, называется модулем Юнга в честь английского ученого Томаса Янга (1773–1829). Янг был первым, кто определил работу как продукт замещения силы, первым использовал слово энергия в его современном смысле и первым показал, что свет — это волна.Он не был первым, кто количественно оценил сопротивление материалов растяжению и сжатию, но он стал самым известным ранним сторонником модуля, который теперь носит его имя. Янг не назвал модуль в честь себя. Он назвал его модулем упругости . Символ модуля Юнга обычно E от французского слова élasticité (эластичность), но некоторые предпочитают Y в честь ученого.
Модуль Юнга
определяется для всех форм и размеров по одному и тому же правилу, но для удобства представим, что стержень длиной 0 и площадью поперечного сечения A растягивается силой F до новой длины ℓ 0 + ∆ℓ.
Растягивающее напряжение — это внешняя нормальная сила на единицу площади (σ = F / A ), а деформация растяжения — частичное увеличение длины стержня (ε = ∆ℓ / ℓ 0 ). Константа пропорциональности, которая связывает эти две величины вместе, представляет собой отношение растягивающего напряжения к растягивающей деформации — модуль Юнга .
То же соотношение справедливо и для сил в противоположном направлении; то есть напряжение, которое пытается сократить объект.
Заменить прилагательное «растяжение» на «сжатие». Нормальная сила на площадь, направленная внутрь (σ = F / A ), называется напряжением сжатия , а частичное уменьшение длины (ε = ∆ℓ / ℓ 0 ) называется деформацией сжатия . Таким образом, модуль Юнга составляет как отношение напряжения сжатия к деформации сжатия. Прилагательное могло быть изменено, но математическое описание — нет.
Единицы измерения модуля Юнга в системе СИ: паскаль [Па]…
| ⎡ ⎢ ⎣ | N | = Па | м | ⎤ ⎥ |
| А | м |
, но для большинства материалов более подходящим является значение гигапаскаль [ГПа].
1 ГПа = 10 9 Па
Коэффициент Пуассона
Растяжение и сжатие — противоположные типы линейной деформации. Продлить — значит стать длиннее. Сокращение означает стать короче. Когда материал растягивается или сжимается под действием линейного напряжения в одном направлении (называемом осью x ), обратная деформация обычно имеет место в перпендикулярных направлениях (оси y и z ). Направление линейного напряжения называется осевым направлением .Все направления, перпендикулярные этому направлению, называются поперечными направлениями .
Осевое разгибание обычно сопровождается поперечным сокращением. Растягивание теста делает его тоньше и длиннее. Так делают китайскую лапшу, вытянутую вручную (拉面, la mian ). Точно так же осевое сокращение обычно сопровождается поперечным растяжением. Если кусок теста расплющить, он станет шире, длиннее и тоньше. Так делают итальянскую свежую пасту ( pasta fresca ).
Отношение поперечной деформации к осевой деформации известно как коэффициент Пуассона (ν) в честь его изобретателя, французского математика и физика Симеона Пуассона (1781–1840). Отрицательный знак необходим, чтобы показать, что изменения обычно противоположного типа (+ растяжение против — сужение). Если придерживаться традиции, согласно которой x — это осевое направление, а y и z — поперечные направления, то коэффициент Пуассона можно записать как…
| ν = — | ∆ y / y 0 | = — | ∆ z / z 0 |
| ∆ x / x 0 | ∆ x / x 0 |
Символ, который, к сожалению, похож на латинскую букву v (vee), на самом деле является греческой буквой ν (nu), которая связана с латинской буквой n (en).
| в | ν | n |
| Латинское «vee» скорость | Греческое «nu» Коэффициент Пуассона | Латинское «en» число |
Типичные значения коэффициента Пуассона находятся в диапазоне от 0,0 до 0,5. Пробка является примером материала с низким коэффициентом Пуассона (почти нулевым). Когда в винную бутылку вставляют пробку, она становится короче, но не толще.(Есть некоторая осевая деформация, но практически отсутствует поперечная.) С другой стороны, резина имеет высокий коэффициент Пуассона (почти 0,5). Когда резиновую пробку вставляют в колбу с химическим веществом, она становится короче на определенную величину и шире почти вдвое. (Осевая деформация сопровождается большой поперечной деформацией.) Пробки можно толкать в бутылки с помощью молотка. Забить резиновую пробку в стеклянную колбу молотком, скорее всего, закончится катастрофой.
Удивительно, но возможны и отрицательные коэффициенты Пуассона.Такие материалы называются ауксетическими . Они увеличиваются в поперечном направлении при растяжении и уменьшаются при сжатии. Большинство ауксетичных материалов представляют собой полимеры с мятой пенистой структурой. Вытягивание пены вызывает разворачивание складок и расширение всей сети в поперечном направлении.
| материал | модуль Юнга | на сжатие прочность | растяжение прочность |
|---|---|---|---|
| алюминий | 70 | 0.040 | |
| морковь, свежая | 0,00136 | 0,000504 | |
| морковь, хранится 1 неделя | 0,00103 | 0,000507 | |
| бетон | 17 | 0,021 | 0,0021 |
| бетон повышенной прочности | 30 | 0.040 | |
| медь | 130 | 0,22 | |
| кость компактная | 18 | 0,17 | 0,12 |
| кость губчатая | 76 | 0,0022 | |
| латунь | 110 | 0,25 | |
| алмаз | 1100 | ||
| стекло | 50–90 | 0.050 | |
| гранит | 52 | 0,145 | 0,0048 |
| золото | 74 | ||
| утюг | 210 | ||
| мрамор | 0,015 | ||
| зефир | 0.000029 | ||
| никель | 170 | ||
| нейлон | 2–4 | 0,075 | |
| дуб | 11 | 0,059 | 0,12 |
| пластик, ♳ ПЭТ | 2,0–2,7 | 0,055 | |
| пластик, ♴ HDPE | 0.80 | 0,015 | |
| пластик, ♵ ПВХ | |||
| пластик, ♶ LDPE | |||
| пластик, ♷ PP | 1,5–2,0 | 0,040 | |
| пластик, ♸ PS | 3,0–3,5 | 0,040 | |
| плутоний | 97 | ||
| фарфор | 0.55 | 0,0055 | |
| кремний | 110 | ||
| карбид кремния | 450 | ||
| сталь, нержавеющая | 0,86 | ||
| сталь конструкционная | 200 | 0,40 | 0,83 |
| сталь высокопрочная | 0.76 | ||
| резина | 0,01–0,10 | 0,0021 | |
| банка | 47 | ||
| титан | 120 | ||
| вольфрам | 410 | ||
| карбид вольфрама | 500 | ||
| уран | 170 |
модуль сдвига
Сила, прикладываемая по касательной (или поперек, или сбоку) к поверхности объекта, называется напряжением сдвига.Возникающая в результате деформация называется деформацией сдвига. Приложение напряжения сдвига к одной грани прямоугольной коробки сдвигает эту сторону в направлении, параллельном противоположной грани, и изменяет прилегающие грани с прямоугольников на параллелограммы.
Коэффициент, который связывает напряжения сдвига (τ = F / A ) к деформации сдвига (γ = ∆ x / y ), называется модулем сдвига , модулем жесткости , или Кулоновский модуль .Обычно он представлен символом G от французского слова glissement (скольжение), хотя некоторые предпочитают вместо этого использовать S от английского слова shear.
Жидкости (жидкости, газы и плазма) не могут сопротивляться напряжению сдвига. Они скорее текут, чем деформируются. Величина, которая описывает, как текучие среды текут в ответ на напряжения сдвига, называется вязкостью и рассматривается в других частях этой книги.
Невозможность сдвига также означает, что жидкости непрозрачны для поперечных волн, таких как вторичные волны землетрясения (также известные как сдвиговые волны или s волны ).Жидкое внешнее ядро Земли было обнаружено с помощью тени, отбрасываемой ею на сети сейсмометров. Типы волн обсуждаются в других разделах этой книги.
Жидкости могут противостоять нормальному стрессу. Это означает, что жидкости и газы прозрачны для первичных волн землетрясения (также известных как волн давления или p-волн ). Твердое внутреннее ядро Земли было обнаружено в сигналах p-волны, которые прошли весь путь от одной стороны Земли через жидкое внешнее ядро к другой стороне.Также слышны зубцы P. Вы можете услышать их, когда они передаются в воздух.
Сопротивление материала нормальному напряжению описывается модулем объемного сжатия, который является следующей темой в этом разделе.
| материал | сдвиг модуль | сдвиг прочность |
|---|---|---|
| алюминий | ||
| бетон | ||
| бетон повышенной прочности | ||
| медь | ||
| кость компактная | ||
| кость губчатая | ||
| латунь | ||
| алмаз | ||
| стекло | ||
| гранит | ||
| золото | ||
| утюг | ||
| мрамор | ||
| зефир | ||
| никель | ||
| нейлон | ||
| дуб | ||
| пластик, ♳ ПЭТ | ||
| пластик, ♴ HDPE | ||
| пластик, ♵ ПВХ | ||
| пластик, ♶ LDPE | ||
| пластик, ♷ PP | ||
| пластик, ♸ PS | ||
| плутоний | ||
| фарфор | ||
| кремний | ||
| карбид кремния | ||
| сталь, нержавеющая | ||
| сталь конструкционная | ||
| сталь высокопрочная | ||
| резина | ||
| банка | ||
| титан | ||
| вольфрам | ||
| карбид вольфрама | ||
| уран |
Модуль объемной упругости
Сила, приложенная равномерно к поверхности объекта, будет равномерно сжимать его.Это изменяет объем объекта без изменения его формы.
Напряжение в этом случае просто описывается как давление ( P = F / A ). Результирующая объемная деформация измеряется по частичному изменению объема (θ = ∆ V / V 0 ). Коэффициент, который связывает напряжение с деформацией при равномерном сжатии, известен как модуль объемного сжатия или модуль сжатия .Его традиционный символ — K от немецкого слова kompression (сжатие), но некоторым нравится использовать B от английского слова bulk, которое является другим словом для обозначения объема.
Модуль объемной упругости — это свойство материалов в любой фазе, но чаще обсуждают модуль объемной упругости для твердых тел, чем для других материалов. У газов есть объемный модуль, который изменяется в зависимости от начального давления, что делает его более важным для термодинамики, в частности, для газовых законов.
Обратный модуль объемного сжатия называется сжимаемостью .Его символ обычно β (бета), но некоторые люди предпочитают κ (каппа). Материал с высокой сжимаемостью испытывает большое изменение объема при приложении давления.
Единицей сжимаемости в системе СИ является обратный паскаль [Па -1 ].
| материал | объем модуль | материал | объем модуль |
|---|---|---|---|
| алюминий | пластик, ♳ ПЭТ | ||
| морковь, свежая | пластик, ♴ HDPE | ||
| морковь, хранится 1 неделя | пластик, ♵ ПВХ | ||
| бетон | пластик, ♶ ПВД | ||
| бетон повышенной прочности | пластик, ♷ PP | ||
| медь | пластик, ♸ PS | ||
| кость компактная | плутоний | ||
| кость губчатая | фарфор | ||
| латунь | кремний | ||
| алмаз | карбид кремния | ||
| стекло | сталь, нержавеющая | ||
| гранит | сталь, конструкционная | ||
| золото | , высокопрочная | ||
| утюг | каучук | ||
| мрамор | банка | ||
| зефир | титан | ||
| никель | вольфрам | ||
| нейлон | карбид вольфрама | ||
| дуб | уран |
масштабирование
- Без гигантских животных
- площадь пропорциональна длине 2
- масса и объем пропорциональны длине 3
- BMR пропорционален массе 3/4
- напряжение пропорционально длине (закон Гука)
- давление пропорционально длине 2 (растяжение желудка, мочевого пузыря)
поверхностное натяжение
| материал | поверхностное натяжение (мкН / м) |
|---|---|
| спирт этиловый (зерновой) | 223. |
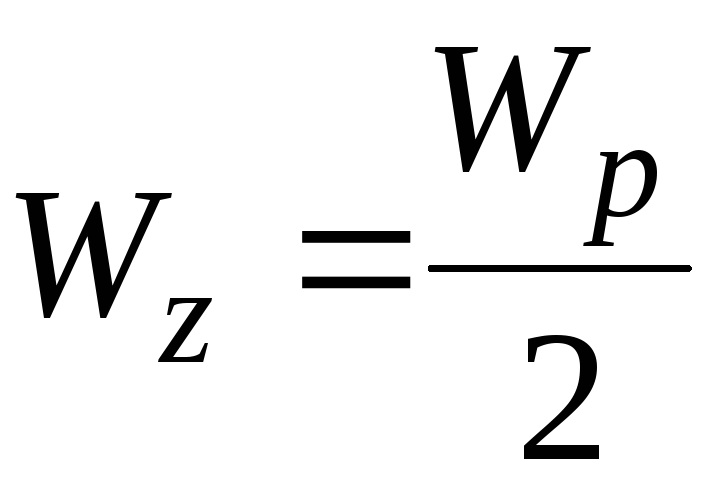
 )
)