Полный расчет балки на прочность и жесткость
Задача
Произвести полный расчет на прочность и проверить жесткость статически определимой двутавровой двухопорной балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [σ]=160 МПа и [τ]=100 МПа, допустимый прогиб балки [f]=l/400
Рис. 1
Решение
Подготовка расчетной схемы к решению задачи:
Определение опорных реакций
Подробно, пример определения опорных реакций для балки рассмотрен здесь
А также в нашем коротком видеоуроке:
Из Σmв=0
Из ΣmА=0
Построение эпюр Q и М
Подробный пример построения эпюр поперечных сил Q и изгибающих моментов M для балки
Видео про расчет значений Q и M для построения эпюр:
youtube.com/embed/cVHD3fHQf0o?rel=0″ frameborder=»0″ allowfullscreen=»»/>
В пролете балки 0 ≤ z2 ≤ l
QII= — RB+ qz2= -52+30∙z2
QII(z=0)= -52 кН
QII(z=l)= -52+30∙4=68 кН
MII=RB∙z2-qz22/2=52z2-30∙z22/2
MII (z=0)= 0
MII (z=l)= -32 кНм
На консоли l ≤ z1≤ (l+a)
QI= — RB+ ql — RA=-52+30∙4-108=-40 кН
MI=RB z1-ql(z1-l/2)+RA(z1-l)=52z1-30∙4(z1-4/2)+108(z1-4)
MI (z=l)= -32 кНм
MI (z=l+a)= 0
По этим данным построены эпюры Q и М.
Короткое видео о том, как надо строить эпюры:
Так как Мmах = 45 кНм, то
Wx≥Mmax / [σ] = 45∙103 / 160∙106= 0,281 м3= 281 см3.
О том, как подбирается сечение балки
По сортаменту выбираем двутавр № 24, для которого Wx = 289 см3, Ix= 3460 см4, Smax = 163 см3, h = 24 см, bп = 11,5 см, t = 0,95 см, d = bc = 0,56 см, h0 = h-2t = 22,1 см.
Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения.
σmax = Mmax / Wx = 45∙103 / 289∙10-6= 156∙106 Па = 156 МПа
Проверка сечения балки по касательным напряжениям
Так как Qmax = 68 кН, то
Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:
Построение эпюры нормальных напряжений
Построение эпюры касательных напряжений
В отношении главных напряжений неблагоприятным является сечение над левой опорой, в котором:
М = -32 кНм и Q = 68 кН.
Значение напряжений в различных точках по высоте двутавра сведены в таблицу 1
Таблица 1
Результаты расчета в примере
Проверка прочности балки по главным напряжениям
Наиболее опасной точкой в неблагоприятном сечении является точка 3. В этой точке σ1=118 МПа и σ3= -16 МПа. Проверяем прочность в этой точке по третьей гипотезе прочности согласно неравенству σ1 — σ3≤ [σ].
В этой точке σ1=118 МПа и σ3= -16 МПа. Проверяем прочность в этой точке по третьей гипотезе прочности согласно неравенству σ1 — σ3≤ [σ].
Так как 118 — ( -16) = 134 < 160, то выбранное сечение удовлетворяет условию прочности и по главным напряжениям.
Расчет перемещений сечений (прогибов балки)
Универсальные уравнения МНП для сечения z:
Опорные условия:
1) при z=0: y(z)=0, следовательно, y0=0
2) при z=l: y(z)=0 находим θ0
откуда θ0= -8,48∙10-3 радиан.
Прогиб в пролете при z=l/2=4/2=2 м.
Аналогично определяется прогиб на конце консоли при z = l + a =4+0,8 = 4,8 м.
Проверка жесткости балки
— пролетной части:
yc=0,98 см < 1/400 = 400/400 = 1 см
— консольной части:
yD=0,33 см < 2a/400 = 2∙80/400 = 0,4 см.
Следовательно, принятая двутавровая балка удовлетворяет требуемому условию жесткости.
Другие примеры решения задач >
| Однопролетные балки на двух шарнирных опорах | ||
| 1 | Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке | Смотреть расчет |
| 2 | Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках | Смотреть расчет |
| 3 | Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 4 | Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 5 | Расчет балки на двух шарнирных опорах при действии изгибающего момента | Смотреть расчет |
| Балки с жестким защемлением на двух опорах | ||
| 6 | Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке | Смотреть расчет |
| 7 | Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках | Смотреть расчет |
| 8 | Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 9 | Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 10 | Расчет балки с жестким защемлением на опорах при действии изгибающего момента | Смотреть расчет |
| Балки с жестким защемлением на одной опоре (консольные) | ||
| 11 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке | Смотреть расчет |
| 12 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 13 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 14 | Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента | Смотреть расчет |
| Балки двухпролетные | ||
| 15 | Расчет двухпролетной с шарнирными опорами при одной сосредоточенной нагрузке | Смотреть |
| 16 | Расчет двухпролетной с шарнирными опорами при двух сосредоточенных нагрузках | Смотреть |
| 17 | Расчет двухпролетной с шарнирными опорами при одной равномерно-распределенной нагрузке | Смотреть |
| 18 | Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке | Смотреть |
| 19 | Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке | Смотреть |
Расчет стальной балки на прогиб
При расчете стальных балок по II-й ГПС (по прогибам) необходимо создавать раскрепления для прогибов:
Информация из справки LIRA SAPR (Справка\Пояснения Сталь\Проверки прогибов):
Проверка прогиба осуществляется сопоставлением реально определенного относительного прогиба (L/f) с максимально возможным для данного конструктивного элемента прогибом.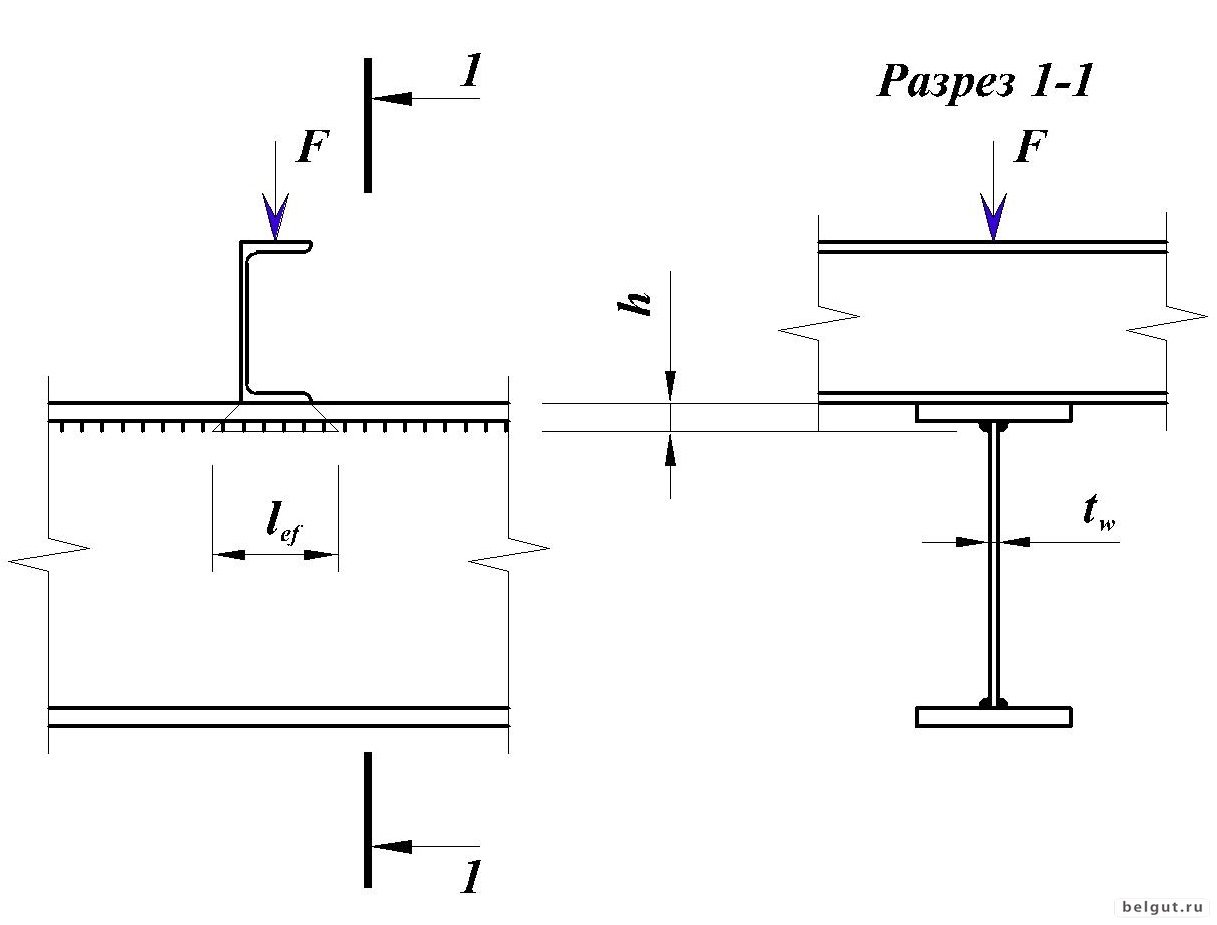
В данной версии проверка выполняется только для балок на основании состава загружений во всех сочетаниях. Учитываются коэффициенты надежности по нагрузке (заданные при формировании РСУ в среде ПК ЛИРА-САПР) и коэффициенты сочетания.
Перемещения, вызванные загружениями с долей длительности 0, в данном расчете не используются.
Прогибы находятся для каждого сечения на основании распределения MY1, MZ1, QY1, QZ1 по длине элемента. Соответственно, увеличение количества расчетных сечений способствует более точному определению прогибов (особенно, если воздействуют сосредоточенные силовые факторы).
В режиме локального расчета элемента (см. справочную систему СТК-САПР) имеется возможность расчета прогибов по огибающим эпюрам изгибающего момента в запас. Это может потребоваться, когда редактируются расчетные сочетания усилий (или нагрузок) и теряется связь с результатами расчета на ПК ЛИРА-САПР основной схемы.
Важно: Предусмотрена возможность определять не чистые перемещения (относительно локальных осей Y и Z в недеформированной схеме), а прогиб относительно двух выбранных условно неподвижных точек – точек раскрепления (в случае консоли, например, относительно одной точки).
Схема к определению прогибов балки с раскреплениями и без раскреплений
На приведенном фрагменте показан механизм определения прогибов (они обозначены как di и dk) в конструктивном элементе с наложенными раскреплениями на элементы.
Если раскрепления не наложены, то прогиб принимается равным полному расстоянию до оси X.
Важно: Если балка (ригель) разбита по длине промежуточными узлами, то для нее необходимо создать конструктивный элемент и раскрепления для проверки прогибов создавать как для конструктивного элемента (т.е. для балки как единого целого). В расчете стальных конструкций коэффициент расчетной длины (и для балок, и для колонн, и для ферм) применяется к длине конечного элемента (КЭ), если не задан конструктивный элемент (КоЭ). Если задан КоЭ, то коэффициент расчетной длины применяется к полной длине КоЭ.
Пример расчета однопролетной балки
Расчётная модель рамы с цельным ригелем и разбитым на отдельные элементы
Согласно нормативной документации прогиб определяется от действия нормативных нагрузок. Поскольку в LIRA SAPR все нагрузки прикладываются к узлам и элементам их расчётными значениями, при определении прогибов программа определяет нормативное значение нагрузок путём деления их на коэффициент надёжности.
Поскольку в LIRA SAPR все нагрузки прикладываются к узлам и элементам их расчётными значениями, при определении прогибов программа определяет нормативное значение нагрузок путём деления их на коэффициент надёжности.
Посмотреть какие приняты коэффициенты надёжности, а также ввести их вручную, если это необходимо, можно в окне параметров расчёта.
Окно параметров расчёта, вызываемое из окна задания параметров для стальных конструкций
Подробнее о корректировке коэффициентов надёжности для расчета прогибов вручную читайте в статье «Коэффициенты к временным нагрузкам при проверке прогиба»
Мозаика результатов проверки назначенных сечений по 2 предельному состоянию
Предельно допустимый L/200=6000/200=30мм
Без задания раскреплений (по абсолютному перемещению узлов балки):
((39,8мм/ к-т надежности по нагрузке)/ 30мм))*100%=((39,8/1,1)/30)*100%=120,6%
С заданием раскреплений (по относительному перемещению узлов балки за вычетом перемещений опорных узлов):
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%
Ручной ввод расчётной длины балки для расчёта прогибов
В диалоговом окне задания характеристик расчёта стальной балки присутствует группа параметров Расчёт по прогибу.
Информация из справки ЛИРА САПР:
Расчет по прогибу – данные для расчета прогиба. Длина пролета авто – вычисляется по положению раскреплений. Длина пролета точно – длина пролета при расчете приравнивается этому числу.
Рассмотрим раму из предыдущего примера, только теперь раскрепления для прогибов назначим для всех конструкций, а расчётные длины будем для первого случая задавать автоматическим способом, а для второго ручным.
Расчётная модель с информацией о назначенных расчётных длинах балок
Результаты расчётов прогибов балок
Предельно допустимый прогиб при длине 6 м L/200=6000/200=30мм
Предельно допустимый прогиб при длине 4 м L/200=4000/200=20мм
Проценты использования по предельному прогибу
Длина балки 6 м:
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%
Длина балки 4 м:
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/20)*100%=139,4%
Расчёт прогибов стрельчатой арки
Пример — рама переменного сечения (РПС) пролётом 18 м. Соединение полурам в коньке — шарнирное, опирание полурам на фундамент — шарнирное.
Соединение полурам в коньке — шарнирное, опирание полурам на фундамент — шарнирное.
Расчётная модель рамы
При этом в параметрах «Дополнительные характеристики» необходимо указать вручную пролет, с которым программа будет сравнивать прогиб (автоматическое определение пролета возможно только для линейных балок, где все конечные элементы (КЭ) конструктивного элемента (КоЭ) лежат на одной оси):
Эпюра перемещений fz ригеля одной полурамы (вдоль местной оси Z1 стержня)
Мозаика перемещений узлов по Z и «Раскрепления для прогибов» (раскреплён только ригель №4)
Результаты определения прогибов в СТК-САПР:
Результаты определения прогибов ригелей №2 и №4
Предельно допустимый L/200=17664/200=88.32 мм
Без задания раскреплений (по абсолютному значению на эпюре прогибов fz):
96.7/17644=1/182 — совпадает с результатом расчёта элемента №2
С заданием раскреплений (по относительному значению на эпюре прогибов fz):
(96. 7-(-6.46))/17644=1/171 — совпадает с результатом расчёта элемента №4
7-(-6.46))/17644=1/171 — совпадает с результатом расчёта элемента №4
Без задания раскреплений (по абсолютному значению перемещений узлов):
99.8/17644=1/177 — не совпадает ни с чем
Вывод: Расчёт на прогибы выполняется в местной системе координат стержня. Прогиб стрельчатых и цилиндрических арок, а также любых криволинейных конструкций, нужно определять по перемещениям узлов в глобальной системе координат и вручную сравнивать с предельно допустимыми значениями.
Расчёт прогибов цилиндрической арки
Пример – цилиндрическая арка пролётом 18 м, стрелой подъёма f = 9 м. Соединение всех элементов между собой — жёсткое, опирание на фундамент — шарнирное.
Нагрузки на арку приложены их расчётными значениями. Значения нагрузок для определения прогибов принимаются согласно СП 20.13330.2016 Нагрузки и воздействия, таблица Д.1 Приложения Д. В данном примере арка является конструкцией покрытия, прогиб которой должен определяться от постоянных и длительных нагрузок (п. 2 табл. Д.1). Для визуализации перемещений от нормативных значений нагрузок, необходимо создать особое РСН с нормативными длительными значениями нагрузок. Нагрузки в данном РСН нужно поделить на коэффициент надёжности, с учётом длительности. На конструкцию действуют два загружения:
2 табл. Д.1). Для визуализации перемещений от нормативных значений нагрузок, необходимо создать особое РСН с нормативными длительными значениями нагрузок. Нагрузки в данном РСН нужно поделить на коэффициент надёжности, с учётом длительности. На конструкцию действуют два загружения:
Загружение 1 — постоянное, коэффициент надёжности 1.1;
Загружение 2 — кратковременное, коэффициент надёжности 1.2, доля длительности 0.35;
Вычислим коэффициенты для перехода к нормативным значениям
Загружение 1 Kn=1/1.1=0.91;
Загружение 2 Kn=1/1.2*0.35=0.292
Таблица РСН с сочетаниями расчётных и нормативных значений нагрузок с учётом длительности.
Мозаика перемещений узлов цилиндрической арки от РСН2
Предельно допустимый прогиб L/200=18000/200=90 мм
Фактический прогиб (по абсолютному значению перемещений узлов): 32.2/18000=1/559 – меньше предельно допустимого значения.
Примечание: если подобная конструкция стоит на своих опорах, то перемещения опорных точек (для получения относительных перемещений) удобно получить через «Мозаику относительных перемещений», указав реперный узел.
Мозаика перемещений узлов в глобальной СК (абсолютных)
Мозаика перемещений узлов в глобальной СК относительно реперного узла
Расчет прогиба балки на двух опорах
Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2.09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.
Способы выполнить расчет и проверку на прогиб
Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.
Просчитать прогиб конструкции можно несколькими способами:
- Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
- Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
- Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.
Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.
Методика выполнения расчета на прогиб
Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.
Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.
В нашем случае балка:
- Имеет прямоугольное сечение S=b*h, длина опирающейся части составляет L;
- Линейка нагружена силой Q, проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ, с прогибом относительно начального горизонтального положения, равным f;
- Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.
Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ, где Е – справочная величина, R— усилие, Δ— величина деформации тела.
Вычисляем моменты инерции и сил
Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е). Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е).
Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.
Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е).
Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил Mmax = q*L*2/8, соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е). Величину b·h2/6 называют моментом инерции и обозначают W. В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.
Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L2/8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.
Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h3/12, где b и h – размеры сечения балки.
Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.
Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.
Формулы для практического использования
На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.
Совет! В вопросе расчета предельного состояния балки по величине прогиба неоценимую услугу оказывают требования СНиПа. Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.
Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.
Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:
- Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
- По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
- По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.
Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L2/(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.
Ответ прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.
Совет! Используйте в своих расчетах существующие ведомственные сборники различных проектных организаций, в которых в сжатом виде сведены все необходимые формулы для определения и расчета предельного нагруженного состояния.
Заключение
Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.
Что еще почитать по теме?
Автор статьи:
Сергей Новожилов — эксперт по кровельным материалам с 9-летним опытом практической работы в области инженерных решений в строительстве.
Понравилась статья? Поделись с друзьями в социальных сетях:
Вконтакте
Одноклассники
Google+
ЭТИ ПРИМЕРЫ ПОМОГУТ СДЕЛАТЬ РАСЧЕТ МЕТАЛЛИЧЕСКОЙ БАЛКИ БЕЗ НАПРЯГА
Металлические балки двутавровые
Кроме повсеместно ведущегося строительства многоэтажных зданий с большим числом квартир, широкое распространение получило сооружение частных домов, причем не только небольших одноэтажных, но и довольно крупных, с двумя и более этажами, иногда и с мансардой наверху или обитаемым чердаком. Для таких домов уже не подходит каркасный метод; материалом часто служит, вместо дерева, кирпич или железобетон. Возведение крупных частных домов должно вестись по всем правилам строительной науки, так как ошибки при проектировании или воплощении проекта могут привести к нежелательным последствиям.
Если строящийся дом представляет собой капитальное здание – из бетона, кирпича, шлакоблока, то для потолочных перекрытий, межэтажных и чердачных, целесообразно применить железобетонные плиты. Наиболее подходящий тип каркаса, способный выдержать вес таких перекрытий, – это каркас, элементом которого является металлическая балка двутаврового профиля.
Именно этот вид проката, установленный своей стенкой вертикально, обладает наибольшей несущей способностью. Естественно, фундамент и стены дома при этом должны быть достаточной прочности, чтобы выдерживать дополнительный вес от 0,5 до 1 тонны – столько металла, в зависимости от количества балок и номера профиля может понадобиться для потолочного перекрытия.
Чтобы избежать лишних затрат и лишнего веса каркаса потолка, а также не допустить обрушения или значительного прогиба балок, необходимо заранее рассчитать их параметры и по результатам расчета подобрать нужный прокат. Расчет сводится к вычислению следующих величин: требуемого момента сопротивления и минимального момента инерции сечения балки, а исходя из последнего – максимального относительного прогиба.
Примечание
РАСЧЕТ ВЕДЕТСЯ ПО ДВУМ ХАРАКТЕРИСТИКАМ – НА ПРОЧНОСТЬ И НА ЖЕСТКОСТЬ. ПО ПОЛУЧЕННЫМ ЗНАЧЕНИЯМ МОМЕНТА СОПРОТИВЛЕНИЯ И МОМЕНТА ИНЕРЦИИ В ТАБЛИЦАХ ГОСТ НАХОДЯТ ТРЕБУЕМЫЙ НОМЕР ПРОКАТА.
Исходные данные для расчетов
Для каркаса потолочных перекрытий малогабаритных частных домов обычно используется двутавр 10 – 20 номеров. Характеристики этих профилей приводятся в ГОСТ 8239-72 – их линейные размеры, площади сечения, максимальные моменты сопротивления по вертикали Wy и минимальные моменты инерции Jy.
Необходимо знать тип плит, которые будут опираться на балочный каркас, а также размеры несущего периметра дома. Можно применить пустотные железобетонные плиты ПК-12-10-8 (1180 х 990 мм, масса 380 кг), а размеры дома взять 4,5 х 6 м. Балки укладываются вдоль короткой стены; шаг укладки при таком размере плит равен 1000 мм (стыки плит совпадают с продольными осями балок, при минимальном зазоре 1 см). Это потребуется для расчета распределенной нагрузки, и исходя из нее – линейной нагрузки на балку, вес самой балки по сравнению с распределенной нагрузкой мал, и при вычислении линейной нагрузки им можно пренебречь.
Распределенная нагрузка при таком типе плит будет равна 325 кгс / м2. К этому надо добавить нагрузку возможных перегородок на верхней стороне перекрытия (75 кгс / м2) и возможную временную нагрузку (200 кгс / м2). В итоге нагрузка, распределенная по площади:
Q = 325 75 200 = 600 кгс / м2,
а линейная нагрузка
q = Q * p = 600 кгс / м = 6 кгс / см.
Эта величина используется в дальнейших расчетах.
Расчет на прогиб
Изгибающий момент для каждой балки вычисляется, исходя из величины линейной нагрузки q, шага укладки балок p и длины перекрываемого пролета L. Так как балки укладываются вдоль короткой стороны, то L = 4,5 м = 450 см (конечно, сами балки длиннее – около 5 м, так как опираются на стены, но шарнирными опорами для них служат именно внутренние края стен).
Искомая величина момента, в таком случае:
My = (q * L2) / 8 = 6 * 4502 / 8 = 151875 кгс * см.
Максимальный момент сопротивления сечения балки можно рассчитать, разделив изгибающий момент на расчетное сопротивление стали – например, марки С235, равное 2150 кгс / см2:
Wy = 151875 / 2150 = 70,6 см3.
Это полученное значение надо сравнить с величиной момента сопротивления сечения двутавровой балки. Из таблицы ГОСТ 8239-72 видно, что вычисленный показатель примерно соответствует (с запасом) моменту сопротивления для профиля 14 (81,7 см3). Следовательно, этот номер проката будет удовлетворять требованиям к прочности балок.
Расчет на жесткость
Жесткость балок характеризуется максимальной величиной прогиба при заданных исходных параметрах. В случае распределенной нагрузки прогиб вычисляется по формуле:
f = 5 * q * L4 / (384 * E * Jy), где
q – линейная нагрузка на балку;
L – длина пролета;
E – модуль упругости материала, для стали С235 равный 2,1 * 106 кгс / см2;
Jy – минимальный момент инерции для данного профиля.
Для принятых ранее исходных данных, с учетом того, что из расчета на прочность наиболее подходящим профилем оказался № 14, для которого Jy, по табличным значениям ГОСТ, равен 572 см4, можно получить:
f = 2,6 см,
а в относительной мере, с учетом того, что длина пролета 450 см – 1 / 172. Это превышает максимально допустимый прогиб, принятый равным 1 / 250.
Поэтому расчет приходится повторить и вычислить прогиб для другого номера проката. Для № 16, у которого момент инерции равен 873 см4, абсолютный прогиб получается 1,74 см, а относительный – 1 / 256, что является приемлемым.
Итоги расчета
Итак, для помещения размером 4,5 х 6 м каркас потолочного перекрытия из железобетонных плит ПК-12-10-8 с распределенной нагрузкой 600 кгс / м2 может быть устроен из двутавровых балок профиля № 16 стали марки С235, расположенных вдоль короткой стороны с шагом 1 м. Можно рассчитать, что для такого здания понадобится 7 таких балок длиной по 5 м, и, зная массу и цену погонного метра, вычислить общую массу балочного каркаса и его стоимость.
Так, для приведенного примера общее количество погонных метров – 35; масса балочного каркаса из профиля № 16 – 525 кг.
Расчет балки на изгиб — Favorit-TK.ru
Рассчитывать балку на изгиб можно несколькими вариантами:
1. Расчет максимальной нагрузки, которую она выдержит
2. Подбор сечения этой балки
3. Расчет по максимальным допустимым напряжениям (для проверки)
Давайте рассмотрим общий принцип подбора сечения балки на двух опорах загруженной равномерно распределенной нагрузкой или сосредоточенной силой.
Для начала, вам необходимо будет найти точку (сечение), в которой будет максимальный момент. Это зависит от опирания балки или же ее заделки. Снизу приведены эпюры изгибающих моментов для схем, которые встречаются чаще всего.
После нахождения изгибающего момента мы должны найти момент сопротивления Wx этого сечения по формуле приведенной в таблице:
Далее, при делении максимального изгибающего момента на момент сопротивления в данном сечении, мы получаем максимальное напряжение в балке и это напряжение мы должны сравнить с напряжением, которое вообще сможет выдержать наша балка из заданного материала.
Для пластичных материалов (сталь, алюминий и т.п.) максимальное напряжение будет равно пределу текучести материала, а для хрупких (чугун) – пределу прочности. Предел текучести и предел прочности мы можем найти по таблицам ниже.
Давайте рассмотрим пару примеров:
1. Вы хотите проверить, выдержит ли вас двутавр №10 (сталь Ст3сп5) длиной 2 метра жестко заделанного в стену, если вы на нем повисните. Ваша масса пусть будет 90 кг.
Для начала нам необходимо выбрать расчетную схему.
На данной схеме видно, что максимальный момент будет в заделке, а поскольку наш двутавр имеет одинаковое сечение по всей длине, то и максимальное напряжение будет в заделке.
Давайте найдем его:
P = m * g = 90 * 10 = 900 Н = 0.9 кН
М = P * l = 0.9 кН * 2 м = 1.8 кН*м
По таблице сортамента двутавров находим момент сопротивления двутавра №10.
Он будет равен 39.7 см3. Переведем в кубические метры и получим 0.0000397 м3.
Далее по формуле находим максимальные напряжения, которые у нас возникают в балке.
б = М / W = 1.8 кН/м / 0.0000397 м3 = 45340 кН/м2 = 45.34 МПа
После того, как мы нашли максимальное напряжение, которое возникает в балке, то мы его может сравнить с максимально допустимым напряжением равным пределу текучести стали Ст3сп5 – 245 МПа.
45.34 МПа < 245 МПа – верно, значит данный двутавр выдержит массу 90 кг.
2. Поскольку у нас получился довольно-таки большой запас, то решим вторую задачу, в которой найдем максимально возможную массу, которую выдержит все тот же двутавр №10 длиной 2 метра.
Если мы хотим найти максимальную массу, то значения предела текучести и напряжения, которое будет возникать в балке, мы должны приравнять (б=245 Мпа = 245 000 кН*м2).
Далее по формуле б = М / W, находим максимальный момент.
М = б * W = 245 000 * 0.0000397 = 9.73 кН * м
Тогда по формуле M = P * L найдем P:
P = 9,73 кН/м / 2м = 4,87 кН = 487 кг
Итак, максимальная масса, которую выдержит двутавр №10 – 487 кг. Число это грубое, поскольку для простоты расчета мы не учитывали различные коэффициенты запаса, поэтому, чтобы подстраховаться, возьмите некий двукратный запас по прочности.
Расчет металлической балки на прогиб: учимся составлять формулы
Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.
Что такое прогиб балки?
Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).
Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.
ν-прогиб сечения C; θ-угол поворота сечения C.
Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.
Метод начальных параметров
Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)
Под начальными параметрами понимаются уже известные перемещения:
- в опорах прогибы равны нулю;
- в жесткой заделке прогиб и угол поворота сечения равен нулю.
Учитывая эти хитрости, их называют еще граничными условиями, определяются перемещения в других частях балки.
Расчет прогибов балки
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:
Реакции опор
Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.
Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:
Система координат
Далее вводим систему координат, с началом в левой части балки (точка А):
Распределенная нагрузка
Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Если бы нагрузка была приложена вот таким способом:
То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:
Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.
Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:
Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
\[ { V }_{ A }=0\quad при\quad x=0 \]
\[ { V }_{ B }=0\quad при\quad x=8м \]
Записываем уравнение метода начальных параметров для сечения C:
\[ E{ I }_{ z }{ V }_{ C }=… \]
Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:
\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]
Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки.{ 4 } } =-2см \]
Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.
На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).
H Beam & I Beam Calculator & Chart (бесплатно)
Что такое двутавровая балка
Двутавровая балка Сталь
Двутавровая балка также называется стальной балкой (Universal Beam), которая представляет собой длинную стальную полосу с крестом -сечение двутавровое. Двутавровая балка делится на обыкновенную двутавровую и световую двутавровую.
Что такое двутавровая балка
Двутавровая балка разработана на основе оптимизации двутавровой стали. Название происходит от того факта, что его сечение совпадает с английской буквой H. Это экономичный высокоэффективный профиль с более разумным соотношением прочности к весу и более оптимизированным распределением площади поперечного сечения.
Каждая часть H-образной стали расположена под прямым углом, поэтому она обладает такими преимуществами, как сильное сопротивление изгибу, экономия затрат, простая конструкция и легкий вес во всех направлениях.
Часто используется в больших зданиях, где требуется большая перехватывающая способность и хорошая стабильность поперечного сечения, например, в высотных зданиях и мастерских. Кроме того, он также широко используется на судах, мостах, подъемно-транспортном оборудовании, кронштейнах, фундаментах оборудования, фундаментных сваях и т. Д.
Двутавровая балка и двутавровая балка
Что касается разницы между двутавровой балкой и двутавровой балкой, вы можете обратиться к статье ниже.
Двутавровая балка по сравнению со сталью (14 анализ различий)
Расчет двутавровой балки и расчет веса двутавровой балки
В этой статье мы в основном обсуждаем, как рассчитать вес двутавровой и двутавровой балок.
Для удобства расчетов мы создали два калькулятора: калькулятор веса двутавровой балки и калькулятор веса двутавровой балки.
С помощью этих двух калькуляторов вы можете легко рассчитать вес двутавровой и двутавровой балок.
Конечно, для более подробных расчетов различных металлических весов вы можете обратиться к следующей статье.
Теоретическая формула расчета веса металла (30 типов металлов)
Кроме того, мы также сделали калькулятор тоннажа листогибочного пресса и калькулятор усилия прессования. Если вам интересно, вы можете воспользоваться им, перейдя по ссылке.
Теперь начните использовать калькулятор для расчета веса профиля.
Если вы устали от использования калькулятора для расчета веса двутавровой балки и двутавровой балки, вы можете обратиться к следующей таблице веса двутавровой балки и таблице веса двутавровой балки.Это позволяет быстрее проверять вес двутавровых и двутавровых балок разных размеров.
Проверить это
Калькулятор свободного луча | ClearCalcs
Как использовать калькулятор свободного луча
Калькулятор луча ClearCalcs позволяет пользователю ввести геометрию и загрузку луча для анализа за несколько простых шагов. Затем он определяет изгибающий момент, диаграммы сдвига и прогиба, а также максимальные требования, используя мощный механизм анализа методом конечных элементов.
Регистрация учетной записи ClearCalcs откроет дополнительные расширенные функции для проектирования и анализа балок и множества других структурных элементов. ClearCalcs позволяет проектировать из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.
Лист разделен на три основных раздела:
- «Ключевые свойства», где пользователь вводит геометрию выбранного сечения и опор балки.
- «Нагрузки», где можно вводить распределенные, точечные и приложенные моментные нагрузки,
- «Сводка», где отображаются основные выходные данные и диаграммы.
Раздел «Комментарии» также включен для того, чтобы пользователь мог оставить какие-либо конкретные примечания по дизайну. Щелчок по любой из меток ввода / свойства дает описательное справочное объяснение.
1. Свойства входных клавиш
Свойства балки и сечения задаются путем ввода непосредственно в поля ввода.
Длина балки — это общая длина балки, включая все пролеты балки, в мм или футах.
Модуль Юнга установлен на значение по умолчанию 200000 МПа или 29000 тысяч фунтов на квадратный дюйм для конструкционной стали, но его можно изменить с помощью Пользователь.
Площадь поперечного сечения зависит от выбранного сечения балки и по умолчанию соответствует значениям для обычной стальной балки.
Второй момент площади (или момент инерции) также зависит от выбранного сечения балки и снова по умолчанию соответствует свойствам обычной стальной балки.
Свойства E, A и Ix для других секций балки можно получить из библиотеки свойств секций ClearCalcs. Кроме того, вы можете создать свой собственный раздел, используя наш бесплатный калькулятор момента инерции.
Положение опор слева позволяет пользователю вводить любое количество опор и указывать их положение по длине балки. Тип опоры может быть закрепленным (фиксированный в перемещении, свободный поворот) или фиксированным (фиксированный как при перемещении, так и при повороте) и выбирается из раскрывающегося меню. Требуется минимум одна фиксированная опора или две штифтовые опоры.
Вычислитель балки также учитывает пролет консолей на каждом конце, поскольку положение первой опоры не обязательно должно быть равно 0 мм, а положение последней опоры не должно быть равно длине балки.
Реакции на каждой из опор автоматически обновляются по мере добавления, изменения или удаления опор в зависимости от указанной нагрузки.
2. Входные нагрузки
Калькулятор поддерживает различные типы нагрузок, которые можно применять в комбинации. Каждой загрузке может быть присвоено имя пользователем.
Знаковое обозначение, используемое для нагружения (показаны положительные значения):
Распределенные нагрузки указываются в единицах силы на единицу длины, кН / м или plf, вдоль балки и могут применяться между любыми двумя точками.В калькуляторе можно использовать два разных типа:
Равномерная нагрузка имеет постоянную величину по всей длине приложения. Следовательно, начальная и конечная величины, указанные пользователем, должны быть одинаковыми.
Линейные нагрузки имеют переменную величину по длине приложения. Различные начальные и конечные величины должны быть указаны пользователем, и они могут использоваться для представления треугольных или трапециевидных нагрузок.
Точечные нагрузки указываются в единицах силы, кН или тысячах фунтов, и площади, приложенной в дискретных точках вдоль балки.Например, они могут представлять реакции других элементов, соединенных с балкой. Пользователь вводит имя, величину и местоположение слева от луча.
На приведенной ниже диаграмме из сводного раздела показана двухпролетная неразрезная балка с линейно распределенной нагрузкой участка и точечной нагрузкой.
3. Итоговые результаты вычислений
После задания нагрузки и геометрии калькулятор автоматически использует механизм конечно-элементного анализа ClearCalcs для определения моментов, поперечных сил и прогибов.Максимальные значения каждого из них выводятся как «Требование момента» , «Требование сдвига», и «Отклонение» вместе с диаграммами по длине балки.
Положительные значения означают отклонение вниз, а отрицательные значения — отклонение вверх. Знаковое соглашение, используемое на диаграммах поперечной силы и изгибающего момента, следующее (показаны положительные значения):
Использование курсора для наведения курсора на любую точку на диаграммах изгибающего момента, поперечной силы или прогиба дает конкретные значения в этом месте вдоль балки.В приведенном ниже примере показаны выходные параметры для двухпролетной неразрезной балки с линейно распределенной коммутационной нагрузкой и точечной нагрузкой.
Калькулятор стальной балки Руководство пользователя
Что нужно знать для использования этого калькулятора — пошаговое руководство
Наш калькулятор прост в использовании, но требует некоторого понимания стальных балок и конструкций. Чтобы облегчить вам жизнь, в этом руководстве пользователя подробно объясняется, какая информация требуется для каждого раздела калькулятора.
1
Детали стальной балки
1.1 Введите длину пролета стальной балки
Введите длину стальной балки.
1.2 Выберите размер стальной балки
Выберите размер стальной балки из раскрывающегося списка. У вас есть выбор «W Beams», «S Beams» или «Американские стандартные каналы».
W-лучи и S-образные лучи имеют характерную I-образную форму, тогда как ширина и глубина более схожи в W-образных лучах, глубина заметно больше, чем ширина в S-образных лучах.Напротив, американские стандартные каналы имеют С-образную форму. Если вы не уверены, какой размер балки использовать, просто позвольте калькулятору стальной балки выбрать размер балки за вас.
1.3 Минимальное напряжение текучести
Выберите 36 000 фунтов на квадратный дюйм или 50 000 фунтов на квадратный дюйм. (Новая сталь обычно составляет 50 000 фунтов на квадратный дюйм.)
2
Детали загрузки
В раскрывающемся меню выберите один из следующих типов нагрузки: «Равномерно распределенная нагрузка», «Частичная равномерно распределенная нагрузка» или «Точечная нагрузка».
- Для равномерно распределенных нагрузок и Частично равномерно распределенных нагрузок , выберите «Сведения о загрузке» в раскрывающемся меню и введите подчиненную ширину нагрузки.Если вы хотите использовать нагрузку, которой нет в раскрывающемся списке, выберите «Другое».
- Множественные нагрузки можно добавить, нажав «Добавить другую нагрузку».
- Для Точечная нагрузка введите размер в Точечную нагрузку по длине балки, имя Точечной нагрузки и Нагрузки.
Вам не нужно добавлять собственный вес стальной балки, поскольку пакет позволяет это автоматически.
Для других грузов вы можете вручную ввести название груза и его вес.
3
Боковые распорки
Если верхняя полка скреплена поперечно расположенными с регулярным интервалом элементами, как правило, по крайней мере, через каждые 2 фута, можно предположить, что она полностью скреплена, при условии, что элементы жесткости прикреплены к балке с помощью крепежных элементов, обеспечивающих надежное соединение. Если это не так, выберите «Нет».
Если ваша балка не будет полностью закреплена, вам необходимо знать длину между ее элементами распорки. Обычно это то же самое, что и длина пролета балки. Однако, если другая балка закреплена перпендикулярно балке по ее длине, это обеспечит фиксацию.В этом случае следует измерить наибольшее расстояние между элементами распорки и ввести эти данные.
4
Пределы прогиба
4.1 Предел прогиба при динамической нагрузке
Это степень прогиба балки под нагрузкой. Обычно это ограничивается диапазоном / 360; однако вы можете изменить это при необходимости.
4.2 Предел прогиба при общей динамической и статической нагрузке
Обычно мы рекомендуем интервал / 240; однако вы можете изменить это при необходимости.
Нажмите кнопку «Выполнить расчет» внизу страницы, чтобы создать отчет о расчетах балки. Если вы используете функцию автоматического выбора, вам будет показан список всех размеров стальных балок, которые подходят для ваших требований.
Калькулятор стальной балки
| Калькулятор стальных балок для проектирования стальных балок
1.2 Выбрать стальную балку
Рассчитайте стальные балки, способные выдерживать указанные ниже нагрузки (расчеты по расчету допустимого напряжения AISC, 9-е издание)
W балки
S балки
Американские стандартные каналы
Выберите конкретную стальную балку
W4X13W5X16W5X19W6X9W6X12W6X20W6X16W6X25W8X10W8X24W8X13W8X31W8X28W8X15W8X35W8X18W8X40W8X21W8X48W8X58W8X67W10X33W10X12W10X39W10X15W10X49W10X45W10X54W10X17W10X19W10X22W10X60W10X26W10X68W10X30W10X77W10X88W10X100W10X112W12X40W12X14W12X16W12X65W12X53W12X45W12X50W12X58W12X19W12X26W12X22W12X30W12X72W12X79W12X87W12X35W12X96W12X106W12X120W12X136W14X22W14X43W14X48W14X30W14X26W14X61W14X53W14X68W14X34W14X90W14X38W14X74W14X99W14X109W14X82W14X120W14X132W16X26W16X36W16X31W16X40W16X45W16X50W16X67W16X57W16X77W16X89W16X100W18X35W18X40W18X50W18X46W18X55W18X60W18X76W18X86W18X65W18X71W18X97W18X106W18X119W18X130W18X143W18X158W18X175W18X192W18X211W21X44W21X50W21X62W21X68W21X57W18X234W21X73W21X83W21X101W21X111W18X258W21X93W21X122W21X132W18X283W21X147W18X311W21X166W21X182W21X201W24X55W24X68W24X62W24X76W24X84W24X104W24X117W24X94W24X103W24X131W24X146W24X162W24X176W24X192W24X207W24X229W24X250W24X279W27X84W27X94W24X306W27X102W27X114W27X146W24X335W27X129W27X161W27X178W24X370W27X194W27X217W27X235W27X258W27X281W30X90W 27X307W30X99W30X108W30X116W27X336W30X124W30X132W30X173W27X368W30X148W30X191W30X211W30X235W30X261W30X292W30X326W27X539W30X357W33X118W33X130W30X391W33X141W33X152W33X201W33X169W33X221W33X241W33X263W33X291W33X318W33X354W36X135W36X150W33X387W36X160W36X170W36X182W36X194W36X210W36X232W36X256W40X149W40X167W40X199W40X183W40X215W40X249W40X277W40X297W40X324W40X362W40X397W40X593S3X7.5S3X5.7S4X9.5S4X7.7S5X10S6X17.25S6X12.5S8X23S8X18.4S10X35S10X25.4S12X50S12X40.8S12X35S12X31.8S15X50S15X42.9S18X70S18X54.7S20X75S20X66S20X96S20X86S24X100S24X90S24X80S24X121S24X106C3X6C3X5C3X4.1C4X7.25C4X5.4C5X9C5X6.7C6X13C6X10.5C6X8.2C7X14.75C7X12.25C7X9.8C8X18.75C8X13.75C8X11.5C9X20C9X15C9X13.4C10X30C10X25C10X20C10X15. 3C12X30C12X25C12X20.7C15X50C15X40C15X33.9 Глубина (дюйм) x вес (фунт / фут)
Beam нагрузки — Поддержка калькулятор Force
Online Force Support Beam Calculator
Калькулятор ниже может быть использована для расчета сил поддержки — R 1 и R 2 — для балок до 6 несимметрично нагружает.
Длина балки (м, футы)
Усилие F1 (Н, фунт f ) расстояние от R 1 (м, фут)
Усилие F2 (Н, фунт f ) расстояние от R 1 (м, фут)
Сила F3 (Н, фунт f ) расстояние от R 1 (м, фут)
Сила F4 ( Н, фунт f ) расстояние от R 1 (м, фут)
Сила F5 (Н, фунт f ) расстояние от R 1 (м, фут)
Сила F6 (Н, фунт f ) расстояние от R 1 (м, фут)
Для балансирующей балки, нагруженной грузами (или другими нагрузочными силами), силы реакции — R — на опорах равно , сила нагрузки — F . Баланс сил может быть выражен как
F 1 + F 2 + …. + F n = R 1 + R 2 (1)
где
F = сила от нагрузки (Н, фунт f )
R = сила от опоры (Н, фунт f )
Дополнительно для балки в балансе алгебраическая сумма моментов равно нулю .Баланс момента может быть выражен как
F 1 a f1 + F 2 a f2 + …. + F n a fn = R a r1 + R a r2 (2)
где
a = расстояние от силы до общей точки отсчета — обычно расстояние до одной из опор (м, футы)
Пример — A балка с двумя симметричными нагрузками
A 10 м длинная балка с двумя опорами нагружена двумя равными и симметричными нагрузками F 1 и F 2 , каждая 500 кг .Опорные силы F 3 и F 4 могут быть рассчитаны
(500 кг) (9,81 м / с 2 ) + (500 кг) (9,81 м / с 2 ) = R 1 + R 2
=>
R 1 + R 2 = 9810 N
= 9,8 кН
2 Примечание! Нагрузка от веса груза — м. — составляет мг, Ньютонов — где г = 9.81 м / с 2 .
При симметричных и равных нагрузках опорные силы также будут симметричными и равными. Используя
R 1 = R 2
, приведенное выше уравнение можно упростить до
R 1 = R 2 = (9810 N) / 2 =
4905 N
= 4,9 кН
Связанные мобильные приложения из Engineering ToolBox
— бесплатные приложения для автономного использования на мобильных устройствах.
Пример — Балка с двумя несимметричными нагрузками
A 10 м длинная балка с двумя опорами нагружена двумя нагрузками, 500 кг расположен 1 м от конца ( R 1 ) , а другой груз 1000 кг расположен на 6 м с того же конца. Баланс сил можно выразить как
(500 кг) (9,81 м / с 2 ) + (1000 кг) (9,81 м / с 2 ) = R 1 + R 2
=>
R 1 + R 2 = 14715 N
= 14.7 кН
Алгебраическая сумма моментов (2) может быть выражена как
(500 кг) (9,81 м / с 2 ) (1 м) + (1000 кг) (9,81 м / с 2 ) (6 м) =? R 1 (0 м) + R 2 (10 м)
=>
R 2 = 6377 (N)
= 6,4 кН
F 3 можно рассчитать как:
R 1 = (14715 Н) — (6377 Н)
= 8338 N
= 8338 N
=3 кН
Вставьте балки в модель Sketchup с помощью Engineering ToolBox Sketchup Extension
Бесплатный калькулятор балки | Калькулятор изгибающего момента, поперечной силы и прогиба
Добро пожаловать в наш бесплатный онлайн-калькулятор диаграмм изгибающего момента и поперечной силы, который может генерировать диаграммы реакций, поперечных сил (SFD) и изгибающих моментов (BMD) консольной балки или просто поддерживаемой балки. Используйте этот калькулятор пролета балки, чтобы определить реакции на опоры, построить диаграмму сдвига и момента для балки и рассчитать прогиб стальной или деревянной балки.Бесплатный онлайн-калькулятор балки для создания реакций, расчета прогиба стальной или деревянной балки, построения диаграмм сдвига и момента балки. Это бесплатная версия нашего полного программного обеспечения SkyCiv Beam. Доступ к нему можно получить из любой из наших Платных учетных записей, которая также включает в себя полное программное обеспечение для структурного анализа.
Используйте интерактивное окно выше, чтобы просмотреть и удалить длину балки, опоры и добавленные нагрузки. Любые внесенные изменения автоматически перерисовывают диаграмму свободного тела для любой балки с опорой или консольной балкой.Калькулятор реакции балки и расчет изгибающего момента будут запущены после нажатия кнопки «Решить» и автоматически сгенерируют диаграммы сдвига и изгибающего момента. Вы также можете щелкнуть отдельные элементы этого калькулятора балки LVL, чтобы редактировать модель.
Калькулятор пролета балки легко рассчитает реакции на опорах. Он может рассчитывать реакции на опорах консольных или простых балок. Это включает в себя расчет реакций консольной балки, которая имеет изгибающий момент, а также силы реакции x, y.
Вышеупомянутый калькулятор пролета стальной балки — это универсальный инструмент для проектирования конструкций, используемый для расчета изгибающего момента в алюминиевой, деревянной или стальной балке. Его также можно использовать в качестве калькулятора несущей способности балки, используя его в качестве калькулятора напряжения изгиба или напряжения сдвига. Он способен выдерживать до 2 различных сосредоточенных точечных нагрузок, 2 распределенных нагрузки и 2 момента. Распределенные нагрузки могут быть расположены так, чтобы они были равномерно распределенными нагрузками (UDL), треугольными распределенными нагрузками или трапециевидными распределенными нагрузками.Все нагрузки и моменты могут быть направленными как вверх, так и вниз по величине, что должно учитывать наиболее распространенные ситуации анализа балок. Расчет изгибающего момента и поперечной силы может занять до 10 секунд, и обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, диаграммой поперечной силы и диаграммой изгибающего момента балки.
Одна из самых мощных функций — использование его в качестве калькулятора отклонения балки (или калькулятора смещения балки). Это можно использовать для наблюдения расчетного прогиба балки с опорой или консольной балки.Возможность добавлять формы сечения и материалы делает его полезным в качестве калькулятора деревянных балок или в качестве калькулятора стальных балок для проектирования балок lvl или i. На данный момент эта функция доступна в SkyCiv Beam, который имеет гораздо больше функций для проектирования деревянных, бетонных и стальных балок.
SkyCiv предлагает инженерам широкий спектр программного обеспечения для структурного анализа и проектирования облаков. Как постоянно развивающаяся технологическая компания, мы стремимся внедрять инновации и совершенствовать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.2) `
Калькулятор момента пучка и поперечной силы
Мы используем эти уравнения вместе с граничными условиями и нагрузками для наших балок, чтобы получить замкнутую форму
решения конфигураций балок, показанных на этой странице (балки с простой опорой и консольные балки). В
Калькулятор балок использует эти уравнения для расчета изгибающего момента, поперечной силы, наклона и прогиба.
диаграммы.
Калькулятор балок — отличный инструмент для быстрой проверки сил в балках.Используйте это, чтобы помочь вам в дизайне
сталь, дерево
и бетонные балки при различных условиях нагружения. Также помните, что вы можете добавлять результаты из балок
все вместе
с использованием
метод
суперпозиция.
Калькулятор стальных, деревянных и бетонных балок
Конечно, не всегда возможно (или практично) получить решение в замкнутой форме для некоторой балки.
конфигурации.Если у вас стальная, деревянная или бетонная балка со сложными граничными условиями и нагрузками
вам лучше решить проблему численно с помощью одного из наших инструментов анализа методом конечных элементов. Если
ты не
беспокоясь о конструктивных кодах и сравнивая потребность в луче и его пропускную способность, попробуйте наши простые в использовании
Калькулятор сдвига и момента.
Если вам нужны полные проверки конструкции с помощью AISC 360, NDS, ASD и LRFD для конструкции стальных или деревянных балок
и вы хотите создать свой следующий луч за считанные минуты, вам может понравиться наш
Инструмент Beam Designer.
Стальная балка по стандарту AISC и деревянная балка NDS
Наша цель с WebStructural — вернуть инженерное сообщество, предоставляя бесплатные,
облачное приложение для проектирования стальных и деревянных балок. Нечего устанавливать, просто перейдите на наш
Бесплатный конструктор стальных и деревянных балок и приступайте к проектированию! Если вам нравится
инструмент
и решите, что хотите сохранить и распечатать проекты, которые можно обновить за 19 долларов.
ежемесячно.Нет долгосрочного контракта. Отмените в любой момент, мы сохраним ваши проекты, и вы сможете повторно подписаться позже
чтобы получить к ним доступ.
Другие бесплатные онлайн-калькуляторы
Мы создаем элегантное и мощное программное обеспечение для проектирования конструкций и структурного анализа. Попробуйте некоторые из наших
другие бесплатные инструменты:
.