Площадь сечения проводов и кабелей в зависимости от силы тока, расчет необходимого сечения кабеля
Если старая проводка вышла из строя нужно её заменить, но прежде чем менять на аналогичную, узнайте, почему произошла проблема со старой. Возможно, что было просто механическое повреждение, или изоляция пришла в негодность, а еще более весомой проблемой является – выход из строя проводки из-за превышения допустимой нагрузки.
Чем отличается кабельная продукция, какие основные характеристики?
Начнем с того, что определяется, какое напряжение в сети, в которой будут работать кабеля. Для бытовых сетей часто применяются кабеля и провода типа ВВГ, ПУГНП (только он запрещен современными требованиями ПУЭ из-за больших допусков по сечению при производстве, до 30%, и допустимой толщине изолирующего слоя 0.3мм, против 0.4 в ПУЭ), ШВВП и другие.
Если отойти от определений провод от кабеля отличается минимально, в основном по определению в ГОСТе или ТУ по которому он производится.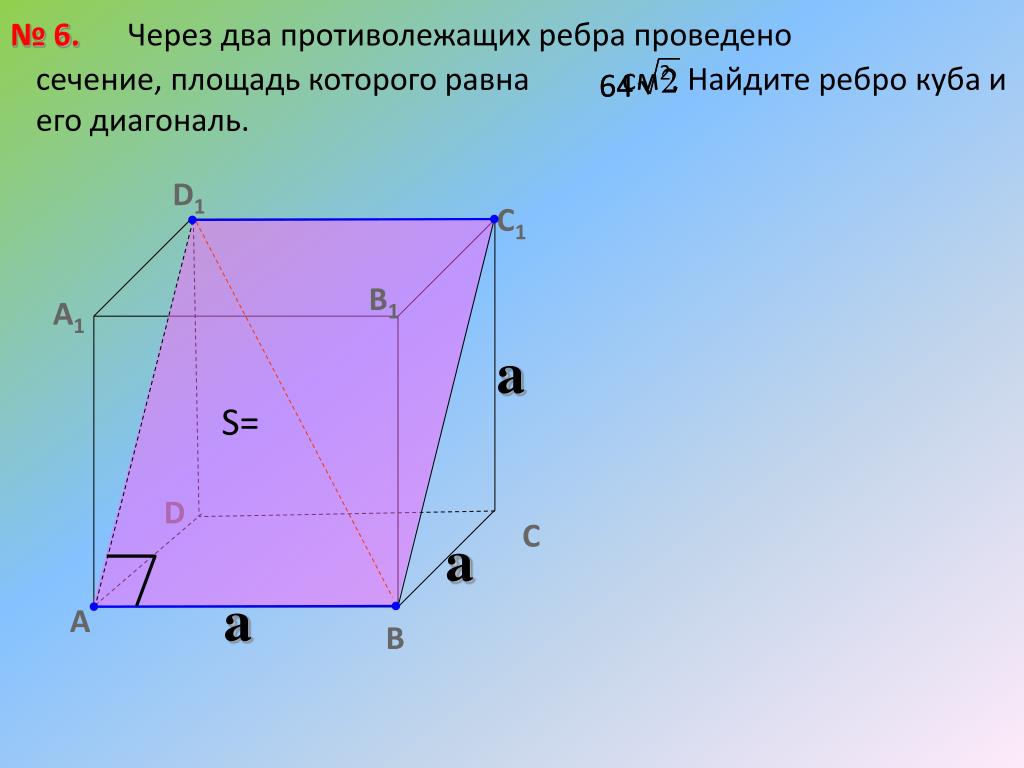 Ведь на рынке есть большое количество проводов с 2-3 жилами и двумя слоями изоляции, например тот же ПУГНП или ПУНП.
Ведь на рынке есть большое количество проводов с 2-3 жилами и двумя слоями изоляции, например тот же ПУГНП или ПУНП.
Допустимое напряжение определяется изоляцией кабеля
Для выбора кабеля кроме напряжения принимают во внимание и условия, в которых он будет работать, для подключения движущегося инструмента и оборудования он должен быть гибким, для подключения неподвижных элементов, в принципе, все равно, но лучше предпочесть кабель с монолитной жилой.
Решающим фактором при покупке является площадь поперечного сечения жилы, она измеряется в мм2, от неё и зависит способность проводника выдерживать длительную нагрузку.
Что влияет на допустимый ток через кабель?
Для начала обратимся к основам физики. Есть такой закон Джоуля-Ленца, он был открыт независимо друг от друга двумя ученными Джеймсом Джоулем (в 1841) и Эмилием Ленцом (в 1842), поэтому и получил двойное название.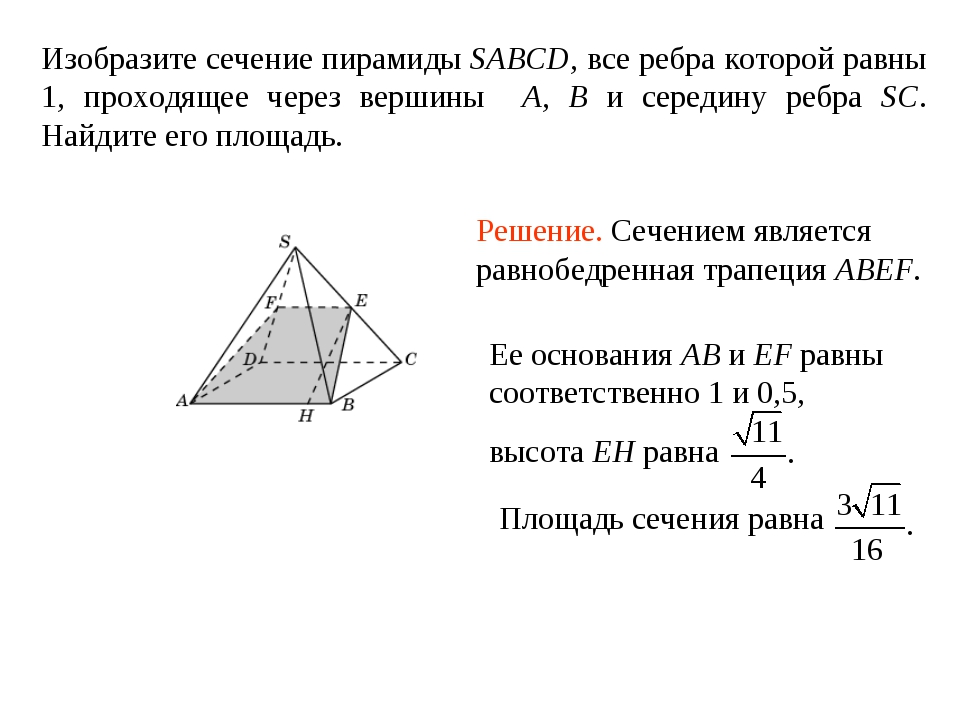 Так вот этот закон количественно описывает тепловое действие электрического тока протекающего через проводник.
Так вот этот закон количественно описывает тепловое действие электрического тока протекающего через проводник.
Если выразить его через плотность тока получится такая формула:
Расшифровка: w – мощность выделения тепла в единице объема, вектор j – плотность тока через проводник измеряется в Амперах на мм2. Для медного провода принимают от 6 до 10 А на миллиметр площади, где 6 – рабочая плотность, а 10 кратковременная. вектор E – напряженность электрического поля. σ – проводимость среды.
Так как проводимость обратно пропорциональна сопротивлению: σ=1/R
Если выразить закон Джоуля-Ленца через количество теплоты в интегральной форме, то:
Таким образом, dQ – количество теплоты, которое выделится за промежуток времени dt в цепи, где протекает ток I, через проводник сопротивлением R.
То есть количество тепла прямо пропорционально току и сопротивлению.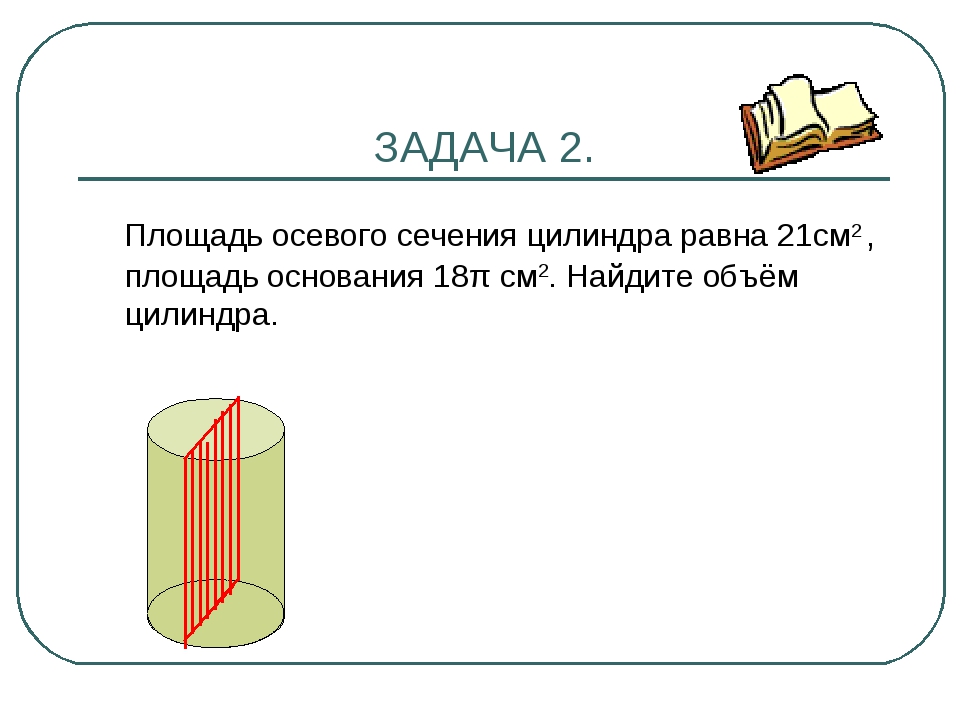 Чем больше ток и сопротивление – тем больше выделяется тепла. Это опасно тем, что в определенный момент количество тепла достигнет такого значения, что у проводов плавится изоляция. Вы могли замечать, что провода дешевых кипятильников ощутимо теплеют во время работы, это оно и есть.
Чем больше ток и сопротивление – тем больше выделяется тепла. Это опасно тем, что в определенный момент количество тепла достигнет такого значения, что у проводов плавится изоляция. Вы могли замечать, что провода дешевых кипятильников ощутимо теплеют во время работы, это оно и есть.
Если выделяется мощность на кабеле, значит, падает и напряжение на его концах, подключенных к нагрузке.
В калькуляторах для расчета сечений кабеля, обычно задаются такие параметры:
Чем больше сопротивление – тем больше упадет напряжение и нагреется кабель, поскольку на нем выделится мощность (P=UI, где U падение напряжения на кабеле, I – ток, протекающий через него).
Все расчеты свелись к току и сопротивлению. Сопротивление проводника вычисляется по формуле:
Здесь: ρ (ро) – удельное сопротивление, l – длина кабеля, S – площадь поперечного сечения.
Удельное сопротивление зависит от структуры металла, величины удельных сопротивлений можно определить из таблицы.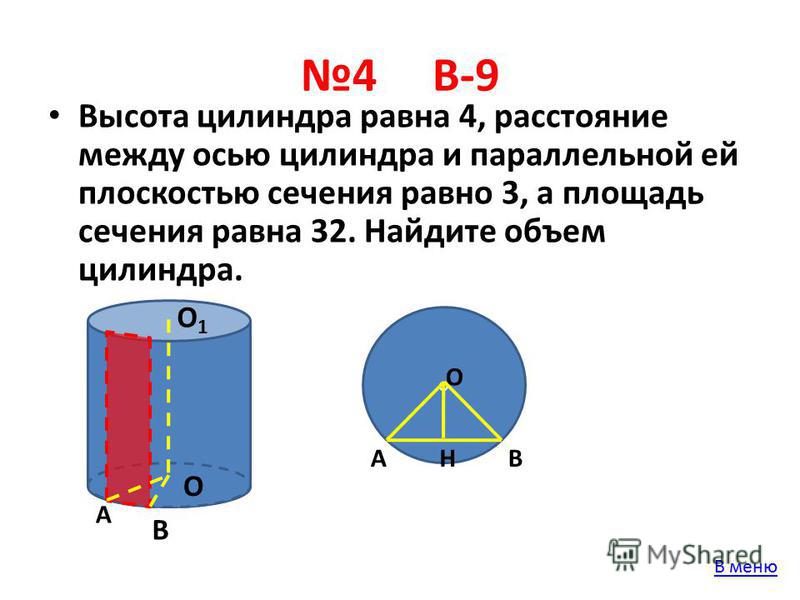
В проводке в основном используются алюминий и медь. У меди сопротивление 1.68*10-8 Ом*мм2/м., а у аллюминия в 1.8 раза больше чем у меди, равняется 2.82*10-8 Ом*мм2/м. Это значит, что алюминиевый провод нагреется почти в 2 раза сильнее, чем медный при одинаковом сечении и токе. Отсюда следует, что для прокладки проводки придется покупать более толстый алюминиевый провод, к тому же жилы легко повредить.
Поэтому медные провода вытеснили с домашней проводки медные, а применение аллюминия в проводке запрещено, разрешается только применение алюминиевых кабелей для монтажа очень мощных электроустановок, потребляющих большой ток, тогда используют провод из аллюминия сечением больше 16 мм2 (смотрите — Почему алюминиевый кабль нельзя использовать в электропроводке)
Как определить сопротивление провода по диаметру жилы?
Бывают случаи, когда площадь поперечного сечения жилы не известна, поэтому можно посчитать по диаметру. Для определения диаметра монолитной жилы можно использовать штангенциркуль, если его нет, то возьмите стержень, например шариковую ручку или гвоздь, намотайте плотно 10 витков провода на него, и измерьте линейкой длину получившейся спирали, разделив эту длину на 10 – вы получите диаметр жилы.
Для определения диаметра монолитной жилы можно использовать штангенциркуль, если его нет, то возьмите стержень, например шариковую ручку или гвоздь, намотайте плотно 10 витков провода на него, и измерьте линейкой длину получившейся спирали, разделив эту длину на 10 – вы получите диаметр жилы.
Для определения общего диаметра многопроволочной жилы, измерьте диаметр каждой жилы и умножьте на их количество.
Дальше считают поперечное сечение по этой формуле:
И вновь возвращаются к этой формуле для расчета сопротивления провода:
Как определить необходимую площадь сечения провода?
Самый простой вариант – определить площадь сечения жил по таблице. Он подходит для расчета не слишком длинных линий проложенных в нормальных условиях (с нормальной температурой окружающей среды). Также так можно подобрать провод для удлинителя. Обратите внимание, что в таблице указаны сечения при определенном токе и мощности в однофазной и трёхфазной сети для аллюминия и меди.
При расчете длинных линий (больше 10 метров) такой таблицей лучше не пользоваться. Нужно провести расчеты. Быстрее всего воспользоваться калькулятором. Алгоритм расчета такой:
Берут допустимые потери по напряжению (не более 5%), это значит что при напряжении в сети 220В и допустимым потерям напряжения в 5% на кабеле падение напряжения (от конца до конца) не должно превышать:
5%*220=11В.
Теперь, зная ток, который будет протекать, мы может вычислить сопротивление кабеля. В двух проводной линии сопротивление умножают на 2, так как ток течет по двум проводам, при линии длиной в 10м, общая длина проводников – 20м.
Отсюда по вышеприведенным формулам вычисляют необходимое поперечное сечение кабеля.
Вы можете сделать это автоматически со своего смартфона, с помощью приложений «Мобильный электрик» и electroDroid. Только в калькуляторе задается не общая длина проводов, а именно длина линии от источника питания к приемнику электричества.
Заключение
Правильно рассчитанная проводка это уже 50% залог её успешного функционирования, вторая половина зависит от правильности монтажа. Следует учитывать все особенности проводки, максимальную потребляемую мощность всеми потребителями. При этом введите запас по допустимому току на 20-40% «на всякий случай».
Сечение арматуры — площадь сечения, таблица для расчета
Горячекатаная арматурная сталь – вид металлопродукции, используемый практически на всех строительных объектах. Назначение арматурных стержней, плоских сеток и объемных каркасов, – повышение устойчивости бетона к нагрузкам различных видов. Эта металлопродукция необходима при возведении фундамента, монолитных стен, производстве железобетонных изделий. Для того чтобы определить прочность арматуры, составить смету, рассчитать массу партии проката, необходим такой показатель, как площадь поперечного сечения. Арматурные стержни имеют поверхность – гладкую или периодического профиля. В обозначении прутов с гладкой поверхностью указывается их наружный диаметр, периодического профиля – номинальный диаметр, который равен наружному диаметру гладкого стержня с равновеликой площадью сечения.
В обозначении прутов с гладкой поверхностью указывается их наружный диаметр, периодического профиля – номинальный диаметр, который равен наружному диаметру гладкого стержня с равновеликой площадью сечения.
Расчет площади сечения арматурных стержней с гладкой поверхностью
Площадь сечения арматурной стали можно просто определить по таблице ГОСТа 5781-82. Однако если при покупке арматуры иногда возникает необходимость узнать эту величину, а таблицы нет под рукой, то можно самостоятельно произвести несложные расчеты. Для них понадобятся штангенциркуль и калькулятор.
С помощью штангенциркуля определим наружный диаметр в миллиметрах. Расчет площади поперечного сечения арматуры производится по формуле:
S = π*dн2/4,
в которой:
- S – площадь сечения, мм2;
- π – постоянная величина, равная 3,14;
- dн – наружный диаметр, мм.
Расчеты для стержней периодического профиля
Арматурная сталь периодического профиля обеспечивает хорошее сцепление с бетоном, поэтому именно она используется в качестве рабочей арматуры, воспринимающей и распределяющей основные нагрузки на бетонную конструкцию.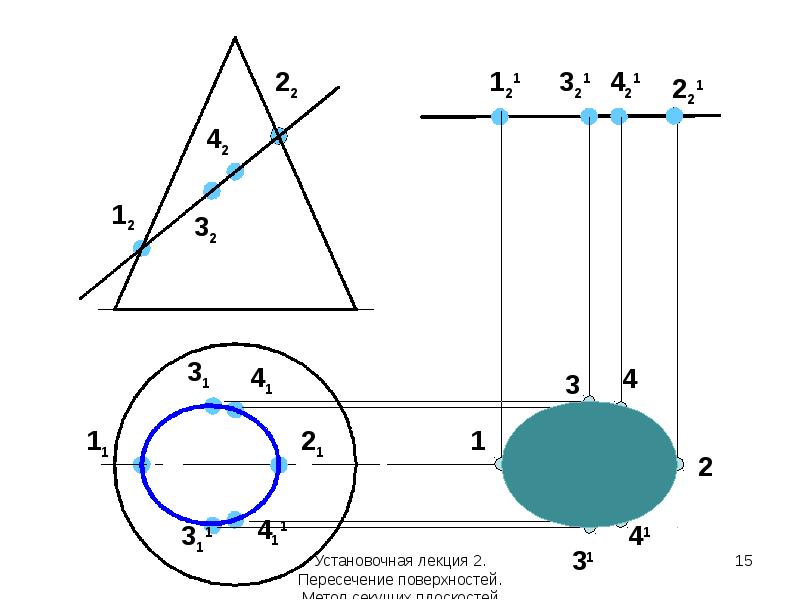
Для определения номинального диаметра производят два измерения с помощью штангенциркуля – по вершинам ребер и по углублениям. Номинальный диаметр равен среднему арифметическому значению этих двух величин. Их суммируют и делят пополам. Площадь сечения определяется по той же формуле, что и в случае стержней с гладкой поверхностью, но вместо наружного значения мы подставляем в формулу значение номинального диаметра.
Вам не понадобится производить расчеты, если под рукой у вас будет таблица площади поперечного сечения стержней арматуры.
| Dном, мм | S, см2 | Dном, мм | S, см2 |
| 6 | 0,283 | 18 | 2,64 |
| 7 | 0,385 | 20 | 3,14 |
| 8 | 0,503 | 22 | 3,8 |
| 10 | 0,785 | 25 | 4,91 |
| 12 | 1,131 | 28 | 6,16 |
| 14 | 1,54 | 36 | 10,18 |
| 16 | 2,01 | 40 | 12,58 |
Как определить поперечное сечение провода? — Общий раздел — Каталог статей по электрике
В быту каждому из нас регулярно приходится иметь дело с электропроводкой и техникой. Нас повсюду окружают всевозможные провода и кабели: в доме, в гараже, в строительных постройках, в автомобиле и так далее. Никакой ремонт не обходится без диагностики или замены электропроводки. В этой статье мы расскажем о том, как определить поперечное сечение одножильных и многожильных кабелей.
Нас повсюду окружают всевозможные провода и кабели: в доме, в гараже, в строительных постройках, в автомобиле и так далее. Никакой ремонт не обходится без диагностики или замены электропроводки. В этой статье мы расскажем о том, как определить поперечное сечение одножильных и многожильных кабелей.
Электрики, имеющие солидный опыт работы в области электромонтажа, редко прибегают к научным методам определения поперечного сечения проводов, прикидывая его «на глаз». Чтобы избежать ошибок, площадь поперечного сечения лучше определять математическими расчетами.
Расчет площади сечения одножильного провода
Сначала разрезаем кабель и замеряем диаметр его жилы, после чего приступаем к расчетам. Так как форма сечения проводов круглая, то рассчитывать ее будем за формулой определения площади круга:
S = π • d²/4, где:
S — искомая площадь поперечного сечения, кв. мм;
d — диаметр жилы, мм;
π — 3,14.
В принципе, формулу можно сразу сократить, разделив π на 4, в итоге мы получим: S = 0,8 • d².
Давайте рассмотрим конкретный случай. Допустим, диаметр жилы составляет 2 мм, тогда S = 0,8 • 2² = 3,2 кв.мм.
Расчет площади сечения многожильного провода
После того, как мы разрежем провод, необходимо подсчитать точное количество жил в связке. Теперь измеряем диаметр одной из них и за уже знакомой формулой S = π • d²/4 определяем площадь ее сечения. Общая площадь поперечного сечения провода будет сумой площади сечения его жил.
Например, мы имеем провод, в котором 25 жил, диаметр каждой из них — 0,5 кв. мм.
s = 0,8 • d² = 0.8 • 0.5 • 0.5 = 0,2 кв. мм.
Следовательно, общая площадь провода будет: S = 25 • s = 25 • 0,2 = 5 кв. мм.
Что касается диаметра жил, то его можно измерить с помощью штангенциркуля или микрометра. Поскольку, не каждый имеет дома эти инструменты, то диаметр жилы будем определять, воспользовавшись линейкой и карандашом. Плотно наматываем жилу на карандаш (чем больше вы сделаете витков, тем точнее будет измерение), а затем линейкой измеряем длину намотки. Полученное число разделяем на количество витков и получаем нужный нам размер диаметра жилы.
Плотно наматываем жилу на карандаш (чем больше вы сделаете витков, тем точнее будет измерение), а затем линейкой измеряем длину намотки. Полученное число разделяем на количество витков и получаем нужный нам размер диаметра жилы.
— — — — —
Статью подготовил: samparam (from Advego — прим. ред.) специально для официального сайта компании «Электро911».
Поперечное сечение. Площадь, длина и примеры расчета
Поперечным сечением называется фигура, образованная пересечением продолговатого тела с воображаемой плоскостью, расположенных перпендикулярно друг другу, т.е. когда тело рассекается строго поперек его длины.
Сечение может иметь простую или сложную форму, а также быть составным.
Площадь и размеры (длина и ширина) поперечного сечения равны соответствующим размерам этой фигуры.
Площадь поперечного сечения
В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.
Формулы для расчета площади основных фигур.
Пример:
Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением.
Для расчета общей площади, сложное сечение раскладывается на простые фигуры:
Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто.
В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:
A=A1+A2+A3-A4
Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м2, см2 или мм2.
Площадь составного сечения
Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым.
Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.
Эти сечения сами по себе тоже являются сложными.
Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.
В результате сложив все составляющие профили, получим площадь всего сечения.
Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.
Длина поперечного сечения
Длиной поперечного сечения называют полную (габаритную) длину фигуры как расстояние по горизонтали между двумя её наиболее удаленными точками.
Длина поперечного сечения обозначается латинской буквой L или l и измеряется стандартно в миллиметрах или сантиметрах.
Ширина сечения определяется аналогично, но обозначается буквой H или h.
При решении задач, длину, ширину и площади поперечного сечения рекомендуется переводить соответственно в метры и м2.
Понятие «поперечное сечение» является одним из основных при расчетах на прочность в сопротивлении материалов и технической механике.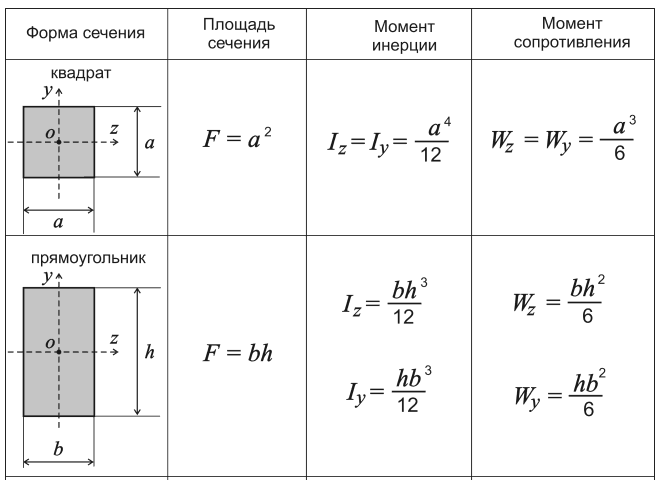
Различают два основных вида расчета площади сечений:
- Геометрический — когда требуется найти площадь сечения тела по известным размерам;
- Прочностной — расчет площади поперечного сечения бруса проводится по условию прочности.
Пример расчета поперечных сечений >
Урок 18. сечения многогранников — Геометрия — 11 класс
Геометрия, 11 класс
Урок №18. Сечения многогранников
Перечень вопросов, рассматриваемых в теме:
Решение задач, сводящихся к доказательству, связанному с построением сечения многогранника
Построение сечения многогранников
Решение задач на нахождение площадей сечений многогранников
Площадь
треугольника S=½hа
трапеции S=½h(а+b)
параллелограмма S=hа
Основная литература:
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10–11 классы : учеб.для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 121-126.
: Просвещение, 2014. – 255, сс. 121-126.
Дополнительная литература:
Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб.для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.
Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.
Открытые электронные ресурс:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Определение: две прямые параллельны, если они лежат в одной плоскости и не пересекаются. Если через две прямые нельзя провести одну плоскость, то такие прямые скрещиваются.
Теорема о параллельности трех прямых: если a∥b, b∥c, то и a∥c. Определение: прямая и плоскость параллельны, если они не имеют общих точек. Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.
Определение: прямая и плоскость параллельны, если они не имеют общих точек. Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.
Определение: две плоскости параллельны, если они не имеют общих точек.
Признак параллельности двух плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости параллельны.
Если две плоскости пересекаются, то их линия пересечения — прямая.
Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны (см. рис.)
Если плоскости α и β пересекаются по прямой a, а плоскости β и γ пересекаются по прямой b, причем a∥b, то плоскости α и γ пересекутся по прямой c∥a∥b.
Следом называется прямая, по которой плоскость сечения пересекает плоскость любой из граней многогранника.
Примеры и разбор решения заданий тренировочного модуля
№1 SABCD – четырехугольная пирамида, в основании которой лежит квадрат ABCD, а две боковые грани SAB и SAD представляют собой прямоугольные треугольники с прямым углом ∠A.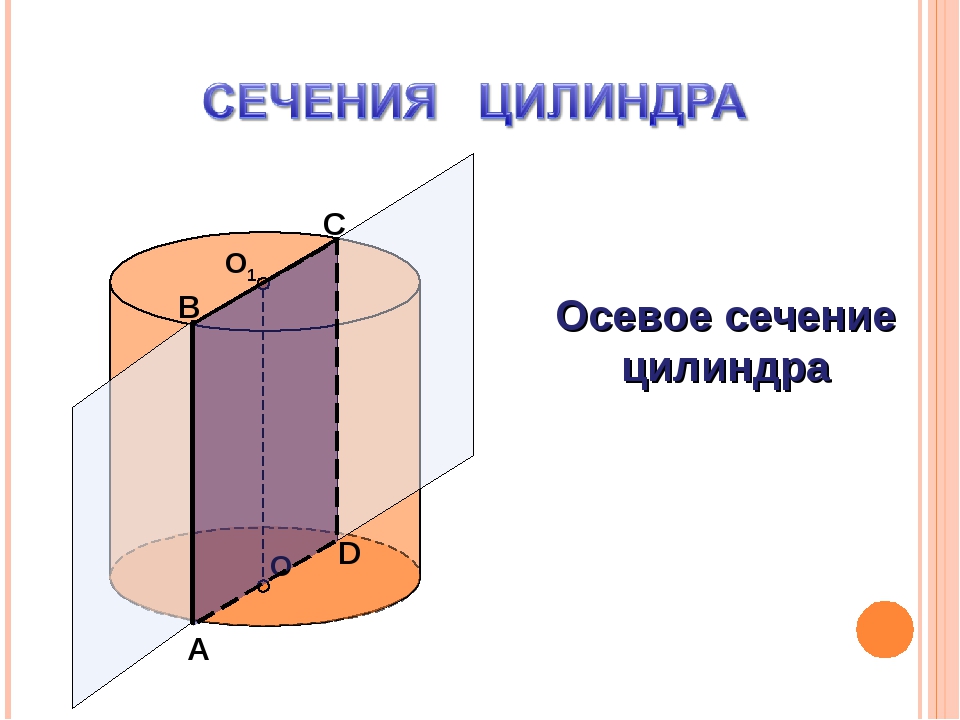 Найдите площадь сечения пирамиды плоскостью α, если SA=AB=a.
Найдите площадь сечения пирамиды плоскостью α, если SA=AB=a.
Решение:
сначала построим сечение по условию задачи.
1)Пусть AC∩BD=O. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Заметим, что т.к. ∠SAB=∠SAD=90∘⇒SA⊥(ABC). Проведем в плоскости SAC прямую OK∥SC. Т.к. O – середина AC, то по теореме Фалеса K – середина SA. Через точку K в плоскости SAB проведем KM∥SB (следовательно, M – середина AB). Таким образом, плоскость, проходящая через прямые OK и KM, и будет искомой плоскостью. Необходимо найти сечение пирамиды этой плоскостью. Соединив точки O и M, получим прямую MN. Т.к. α∥(SBC),то α пересечет плоскость SCD по прямой NP∥SC (если NP∩SC≠∅, то α∩(SBC)≠∅, что невозможно ввиду их параллельности). Таким образом, KMNP – искомое сечение, причем KP∥AD∥MN⇒ это трапеция.
2)Т.к. все точки K,M,N,P – середины отрезков SA,AB,CD,SD соответственно, то: а) MN=AD=a б) KP=1/2AD=a/2 в) KM=1/2SB=a 2/2 Заметим, что по теореме о трех перпендикулярах SB⊥BC⇒KM⊥MN.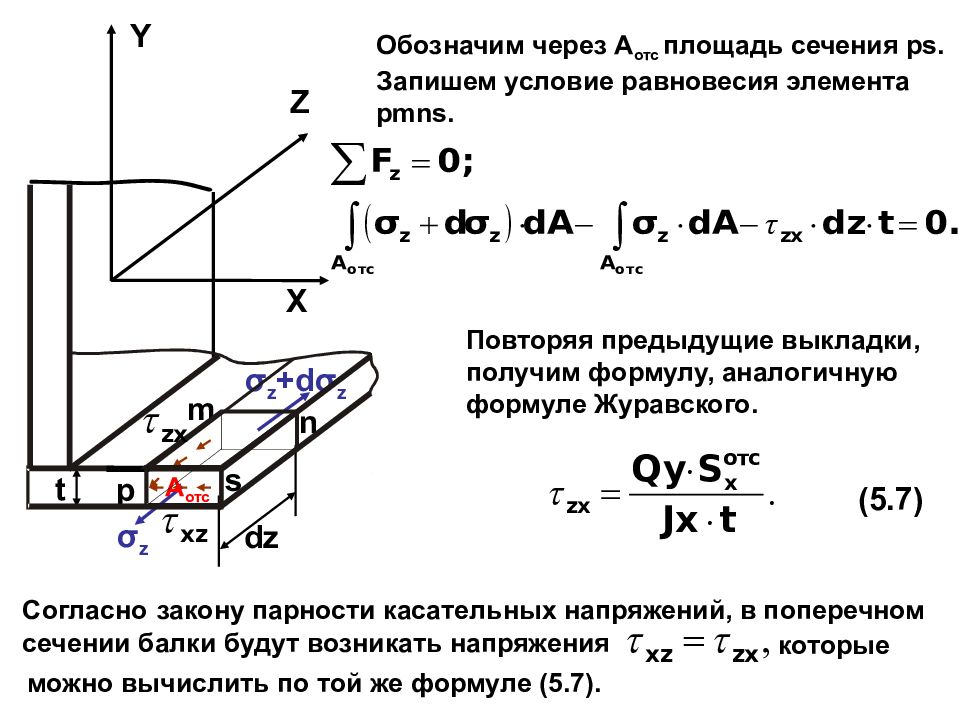 Таким образом, KMNP – прямоугольная трапеция. SKMNP=(KP+MN)* KM/ 2 =3 a2/8
Таким образом, KMNP – прямоугольная трапеция. SKMNP=(KP+MN)* KM/ 2 =3 a2/8
Ответ:3 a2/8
№2 Найди площадь сечения прямой призмы, проходящей через середины ребер, если =120°, АВ=5 см, ВС=3см и наибольшая из площадей боковых граней равна 35см2 .
Решение:
боковая грань прямой призмы является прямоугольником.
Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.
То есть большая боковая грань содержит большую сторону основания.
По условию =120°, – тупой, а поскольку напротив большей стороны лежит больший угол, то большей стороной основания будет сторона АС. Вычислим длину стороны АС по теореме косинусов.
Получим, что длина стороны АС=7см.
Зная большую сторону основания и площадь наибольшей боковой грани призмы, длину высоты призмы вычислить нетрудно.
Получим, что длина высоты призмы равна .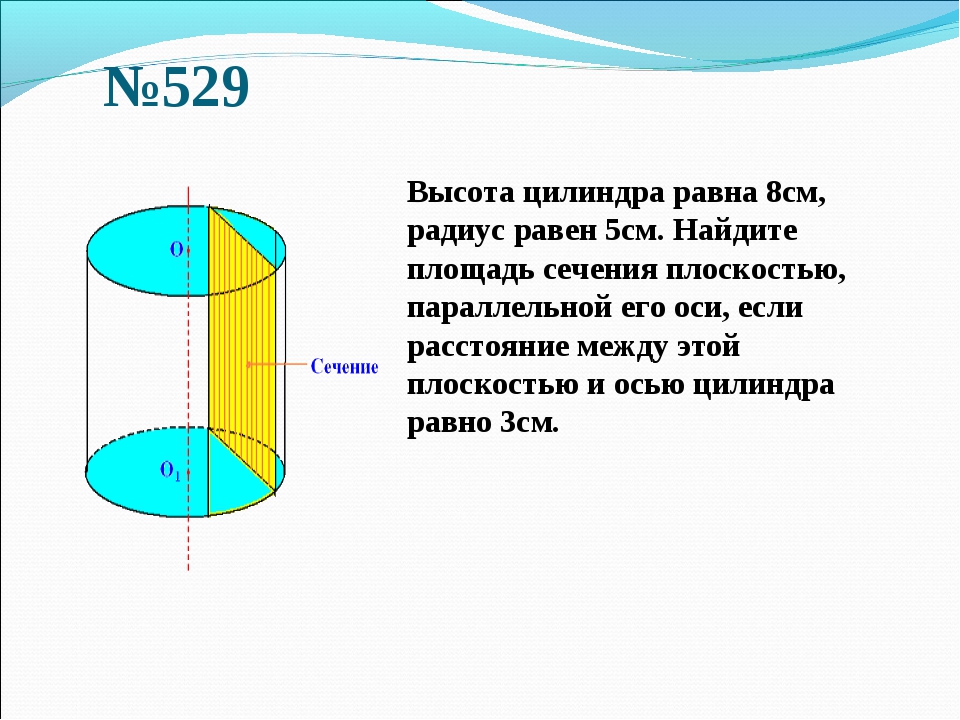
Найдем площадь основания, а оно равно площади сечения, по формуле .
Мы воспользуемся второй формулой. Получим, что площадь основания равна .
Ответ: 15 /4 см2
№3 На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ:QB=1:2. Точка P — середина ребра AS.
Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.
Решение:
пусть сторона основания пирамиды равна 3а, а высота пирамиды равна h. Тогда площадь сечения DSB равна
S=BD*SO/2= 3 =6
откуда ah=2 .
Площадь сечения DPQ равна
Ответ:
№4
Дана правильная треугольная пирамида SABC с вершиной S. Через середину ребра AC и точки пересечения медиан граней ASB и CSB проведена плоскость. Найдите площадь сечения пирамиды этой плоскостью, если AB=21,AS=12 .
Решение:
пусть LK∩SO=H. Тогда по теореме о трех перпендикулярах HK⊥AC как наклонная (HO⊥(ABC),OK⊥AC как проекция).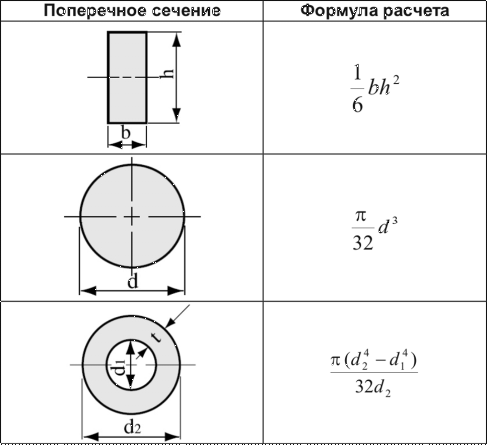 Следовательно, и LK⊥AC.
Следовательно, и LK⊥AC.
Тогда SALC=AC⋅LK/2 Рассмотрим △SKB: BK=AB⋅ /2=21 /2⇒cosB=7 /12 .
Тогда по теореме косинусов для △KLB: KL2=729/4⇒KL=27/2
Значит, SALC=567/4=141,75
Ответ : 141,75
№5
Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре AA1 отмечена точка K так, что AK : KA1 = 1 : 2. Плоскость α проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD1 в точке M, АВ=4, АА1=6. Найдите площадь сечения.
Решение:
По теореме о трех перпендикулярах прямые BM и AC перпендикулярны, а значит, прямые BM и KL перпендикулярны. Площадь четырехугольника, диагонали которого взаимно перпендикулярны, равна половине произведения диагоналей. Найдем их: KL=AC=4 как диагональ квадрата, лежащего в основании призмы, тогда
по теореме Пифагора.
Тогда
Ответ: 8
Сечение провода (кабеля) по диаметру: формула, таблица
По идее, диаметр проводников должен соответствовать заявленным параметрам. Например, если указано на маркировке, что кабель 3 x 2,5, значит сечение проводников должно быть именно 2,5 мм2. На деле получается, что отличаться реальный размер может на 20-30%, а иногда и больше. Чем это грозит? Перегревом или оплавлением изоляции со всеми вытекающими последствиями. Потому, перед покупкой, желательно узнать размер провода, чтобы определить его поперечное сечение. Как именно считать сечение провода по диаметру и будем выяснять дальше.
Содержание статьи
Как и чем измерить диаметр провода (проволоки)
Для измерения диаметра провода подойдет штангенциркуль или микрометр любого типа (механический или электронный). С электронными работать проще, но они есть не у всех. Измерять надо саму жилу без изоляции, потому предварительно ее отодвиньте или снимите небольшой кусок. Это можно делать, если продавец разрешит. Если нет — купите небольшой кусок для тестирования и проводите измерения на нем. На очищенном от изоляции проводнике замеряете диаметр, после чего можно определить реальное сечение провода по найденным размерам.
Это можно делать, если продавец разрешит. Если нет — купите небольшой кусок для тестирования и проводите измерения на нем. На очищенном от изоляции проводнике замеряете диаметр, после чего можно определить реальное сечение провода по найденным размерам.
Измерения диаметра провода микрометром более точные, чем механическим штангенциркулем
Какой измерительный прибор в данном случае лучше? Если говорить о механических моделях, то микрометр. У него точность измерений выше. Если говорить об электронных вариантов, то для наших целей они оба дают вполне достоверные результаты.
Если нет ни штангенциркуля, ни микрометра, захватите с собой отвертку и линейку. Придется зачищать довольно приличный кусок проводника, так что без покупки тестового образца на этот раз вряд ли обойдетесь. Итак, снимаете изоляцию с куска провода 5-10 см. Наматываете проволоку на цилиндрическую часть отвертки. Витки укладываете вплотную один к другому, без зазора. Все витки должны быть полными, то есть «хвосты» провода должны торчать в одном направлении — вверх или вниз, например.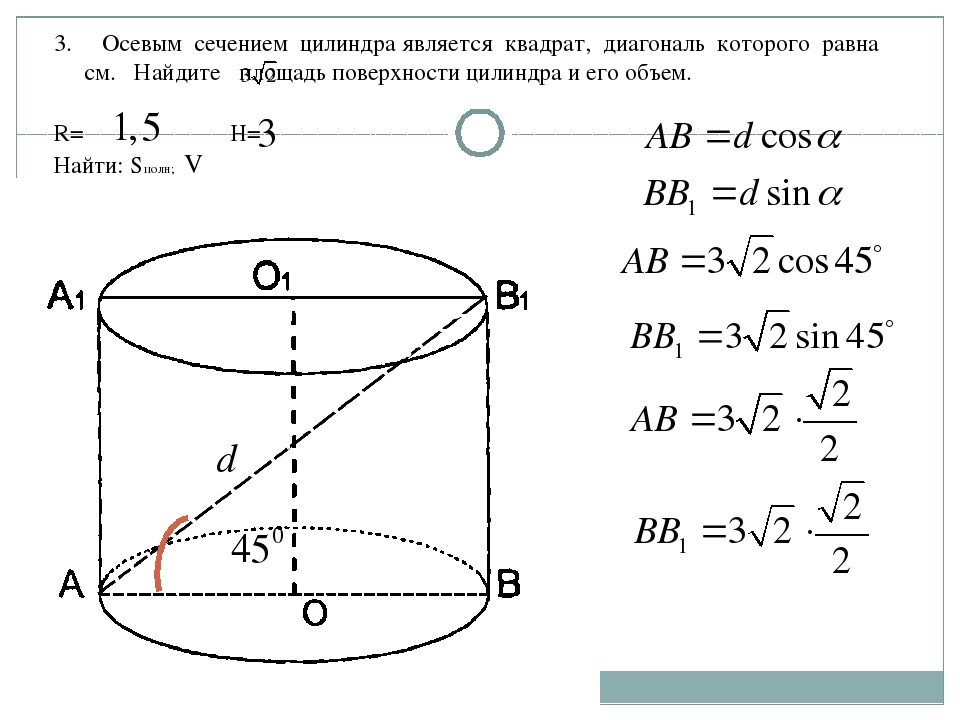
Определение диаметра провода при помощи линейки
Количество витков не важно — около 10. Можно больше или меньше, просто на 10 делить проще. Витки считаете, затем прикладываете полученную намотку к линейке, совместив начало первого витка с нулевой отметкой (как на фото). Измеряете длину участка, занятого проводом, потом его делите на количество витков. Получаете диаметр провода. Вот так все просто.
Например, посчитаем каков размер проволоки, изображенной на фото выше. Количество витков в данном случае — 11, занимают они 7,5 мм. Делим 7,5 на 11, получаем 0,68 мм. Это и будет диаметр данного провода. Далее можно искать сечение этого проводника.
Ищем сечение провода по диаметру: формула
Провода в кабеле имеют в поперечном сечении форму круга. Потому при расчетах пользуемся формулой площади круга. Ее можно найти используя радиус (половину измеренного диаметра) или диаметр (смотрите формулу).
Потому при расчетах пользуемся формулой площади круга. Ее можно найти используя радиус (половину измеренного диаметра) или диаметр (смотрите формулу).
Определяем сечение провода по диаметру: формула
Например, посчитаем площадь поперечного сечения проводника (проволоки) по размеру, рассчитанному ранее: 0,68 мм. Давайте сначала используем формулу с радиусом. Сначала находим радиус: делим диаметр на два. 0,68 мм / 2 = 0,34 мм. Далее эту цифру подставляем в формулу
S = π * R2 = 3,14 * 0,342 = 0,36 мм2
Считать надо так: сначала возводим в квадрат 0,34, потом умножаем полученное значение на 3,14. Получили сечение данного провода 0,36 квадратных миллиметров. Это очень тонкий провод, который в силовых сетях не используется.
Давайте посчитаем сечение кабеля по диаметру, используя вторую часть формулы. Должно получиться точно такое же значение. Разница может быть в тысячные доли из-за разного округления.
S = π/4 * D2 = 3. 14/4 * 0,682 = 0,785 * 0,4624 = 0,36 мм2
14/4 * 0,682 = 0,785 * 0,4624 = 0,36 мм2
В данном случае делим число 3,14 на четыре, потом возводим диаметр в квадрат, две полученные цифры перемножаем. Получаем аналогичное значение, как и должно быть. Теперь вы знаете, как узнать сечение кабеля по диаметру. Какая из этих формул вам удобнее, ту и используйте. Разницы нет.
Таблица соответствия диаметров проводов и их площадь сечения
Проводить расчеты в магазине или на рынке не всегда хочется или есть возможность. Чтобы не тратить время на расчеты или не ошибиться, можно воспользоваться таблицей соответствия диаметров и сечений проводов, в которой есть наиболее распространенные (нормативные) размеры. Ее можно переписать, распечатать и захватить с собой.
| Диаметр проводника | Сечение проводника |
|---|---|
| 0,8 мм | 0,5 мм2 |
| 0,98 мм | 0,75 мм2 |
| 1,13 мм | 1 мм2 |
| 1,38 мм | 1,5 мм2 |
| 1,6 мм | 2,0 мм2 |
| 1,78 мм | 2,5 мм2 |
| 2,26 мм | 4,0 мм2 |
| 2,76 мм | 6,0 мм2 |
| 3,57 мм | 10,0 мм2 |
| 4,51 мм | 16,0 мм2 |
| 5,64 мм | 25,0 мм2 |
Как работать с этой таблицей? Как правило, на кабелях есть маркировка или бирка, на которой указаны его параметры. Там указывается маркировка кабеля, количество жил и их сечение. Например, ВВНГ 2х4. Нас интересуют параметры жилы а это цифры, которые стоят после знака «х». В данном случае заявлено, что есть два проводника, имеющих поперечное сечение 4 мм2. Вот и будем проверять, соответствует ли эта информация действительности.
Там указывается маркировка кабеля, количество жил и их сечение. Например, ВВНГ 2х4. Нас интересуют параметры жилы а это цифры, которые стоят после знака «х». В данном случае заявлено, что есть два проводника, имеющих поперечное сечение 4 мм2. Вот и будем проверять, соответствует ли эта информация действительности.
Как работать с таблицей
Чтобы проверить, проводите измерение диаметра любым из описанных методов, после сверяетесь с таблицей. В ней указано, что при таком сечении в четыре квадратных миллиметра, размер провода должен быть 2,26 мм. Если измерения у вас такие же или очень близкие (погрешность измерений существует, так как приборы неидеальные), все нормально, можно данный кабель покупать.
Заявленные размеры далеко не всегда соответствуют реальным
Но намного чаще фактический диаметр проводников значительно меньше заявленного. Тогда у вас два пути: искать провод другого производителя или взять большего сечения. За него, конечно, придется переплатить, но первый вариант потребует достаточно большого промежутка времени, да и не факт, что вам удастся найти соответствующий ГОСТу кабель.
Второй вариант потребует больше денег, так как цена существенно зависит от заявленного сечения. Хотя, не факт — хороший кабель, сделанный по всем нормам, может стоит еще дороже. Это и понятно — расходы меди, а, часто, и на изоляцию, при соблюдении технологии и стандартов — значительно больше. Потому производители и хитрят, уменьшая диаметр проводов — чтобы снизить цену. Но такая экономия может обернуться бедой. Так что обязательно проводите измерения перед покупкой. Даже и проверенных поставщиков.
И еще: осмотрите и пощупайте изоляцию. Она должна быть толстой, сплошной, иметь одинаковую толщину. Если кроме изменения диаметра еще и с изоляцией проблемы — ищите кабель другого производителя. Вообще, желательно найти продукцию, отвечающую требованиям ГОСТа, а не сделанную по ТУ. В этом случае есть надежда на то, что кабель или провод буде служить долго и без проблем. Сегодня это сделать непросто, но если вы разводите проводку в доме или подключаете электричество от столба, качество очень важно. Потому, стоит, наверное, поискать.
Потому, стоит, наверное, поискать.
Как определить сечение многожильного провода
Иногда проводники используются многожильные — состоящие из множества одинаковых тонких проволочек. Как посчитать сечение провода по диаметру в этом случае? Да точно также. Проводите измерения/вычисления для одной проволоки, считаете их количество в пучке, потом умножаете на это число. Вот вы и узнаете площадь поперечного сечения многожильного провода.
Сечение многожильного провода считается аналогично
Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия
Основные определения и свойства цилиндра
Рассмотрим две паралллельные плоскости паралллельные плоскости α и β и произвольную окружность радиуса r с центром в точке O , лежащую в плоскости α (рис. 1).
Рис.1
Если из каждой точки окружности опустить перпендикуляр на плоскость β, то основания этих перпендикуляров образуют на плоскости β окружность радиуса r, центр O1 которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).
Рис.2
Определение 1.
Отрезок перпендикуляра, опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра. | |
Совокупность всех образующих цилиндра называют цилиндрической поверхностью. | |
Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром. | |
Отрезок OO1 называют осью цилиндра . | |
Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра. | |
Расстояние между плоскостямиРасстояние между плоскостями α и β , называют высотой цилиндра. | |
Круги с центрами O и O1 на плоскостях α и β , называют основаниями цилиндра. |
Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра. Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра.
Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.
Замечание 3. Прямая OO1 является осью симметрии цилиндра, а середина отрезка OO1 является центром симметрии цилиндра.
Сечения цилиндра
Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).
Рис.3
На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA1B1B .
Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .
Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).
Рис.4
Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .
Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».
Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра
Для цилиндра с радиусом r и высотой h (рис. 5)
Рис.5
введем следующие обозначения
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:
Sосн = πr2,
V = Sоснh = πr2h,
Sбок= 2πrh,
Sполн = 2πr2 + 2πrh =
= 2π(r + h).
Замечание 7. Формула объема цилиндра V = πr2h может быть получена из формулы объема правильной n – угольной призмыформулы объема правильной n – угольной призмы
при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Свойства поперечного сечения | MechaniCalc
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Поведение элемента конструкции определяется его материалом и геометрией. Поперечное сечение и длина конструктивного элемента влияют на то, насколько этот элемент отклоняется под нагрузкой, а поперечное сечение определяет напряжения, которые существуют в элементе при данной нагрузке.
Недвижимость участков
Центроид
Центроид формы представляет собой точку, вокруг которой равномерно распределена площадь сечения.Если область дважды симметрична относительно двух ортогональных осей, центр тяжести лежит на пересечении этих осей. Если область симметрична только относительно одной оси, то центр тяжести лежит где-то вдоль этой оси (необходимо вычислить другую координату). Если точное местоположение центроида не может быть определено путем осмотра, его можно рассчитать следующим образом:
где dA представляет собой площадь бесконечно малого элемента, A — общая площадь поперечного сечения, а x и y — координаты элемента dA относительно интересующей оси.
Центроидные положения общих поперечных сечений хорошо задокументированы, поэтому обычно нет необходимости рассчитывать местоположение с помощью приведенных выше уравнений.
Если поперечное сечение состоит из набора основных форм, центроидальное положение которых известно относительно некоторой контрольной точки, то центральное положение составного поперечного сечения можно рассчитать как:
где x c, i и y c, i — прямоугольные координаты центра тяжести участка i th относительно опорной точки, а A i — площадь участка i th . раздел.
Центроидное расстояние
Центроидное расстояние , c — это расстояние от центра тяжести поперечного сечения до крайнего волокна. Центроидное расстояние в направлении y для прямоугольного поперечного сечения показано на рисунке ниже:
Обычно центроидное расстояние используется:
Первый момент области
Первый момент области относительно интересующей оси рассчитывается как:
| Q x = ∫ y dA | Q y = ∫ x dA |
где Q x — это первый момент вокруг оси x, а Q y — это первый момент вокруг оси y.Если область состоит из набора основных форм, чьи центроидные положения известны относительно интересующей оси, то первый момент составной области можно рассчитать как:
Обратите внимание, что первый момент площади используется при вычислении центра тяжести поперечного сечения относительно некоторого начала координат (как обсуждалось ранее). Первый момент также используется при вычислении значения напряжения сдвига в определенной точке поперечного сечения.В этом случае первый момент вычисляется для области, которая составляет меньшую часть поперечного сечения, где область ограничена интересующей точкой и крайним волокном (верхним или нижним) поперечного сечения. Первый момент рассчитывается относительно оси, проходящей через центр тяжести поперечного сечения.
На рисунке выше заштрихованная синяя область представляет собой интересующую область в пределах всего поперечного сечения. Первый момент этой области относительно оси x (которая проходит через центр тяжести поперечного сечения, точку O на рисунке выше) рассчитывается как:
Если центральное положение интересующей области известно, то первый момент области относительно оси можно рассчитать как (см. Рисунок выше):
Q cx = y c1 A 1
Следует отметить, что первый момент области будет положительным или отрицательным в зависимости от положения положения области относительно оси интереса.Следовательно, первый момент всей площади поперечного сечения относительно его собственного центроида будет равен нулю.
Момент инерции площади
Второй момент площади, более известный как момент инерции , I, поперечного сечения, является показателем способности конструктивного элемента сопротивляться изгибу. (Примечание 1) I x и I y — моменты инерции относительно осей x и y, соответственно, и рассчитываются по формуле:
| I x = ∫ y 2 dA | I y = ∫ x 2 dA |
где x и y — координаты элемента dA относительно интересующей оси.
Чаще всего моменты инерции рассчитываются относительно центра тяжести сечения. В этом случае они обозначаются как центроидных моментов инерции и обозначаются как I cx для инерции относительно оси x и I cy для инерции относительно оси y.
Моменты инерции общих поперечных сечений хорошо задокументированы, поэтому обычно нет необходимости рассчитывать их с помощью приведенных выше уравнений. Свойства нескольких общих сечений приведены в конце этой страницы.
Если поперечное сечение состоит из набора основных форм, все центроиды которых совпадают, то момент инерции составного сечения является просто суммой отдельных моментов инерции. Примером этого является балка коробчатого сечения, состоящая из двух прямоугольных секций, как показано ниже. В этом случае внешняя часть имеет «положительную площадь», а внутренняя часть имеет «отрицательную площадь», поэтому составной момент инерции представляет собой вычитание момента инерции внутренней части из внешней части.
В случае более сложного составного поперечного сечения, в котором центральные положения не совпадают, момент инерции может быть вычислен с использованием теоремы о параллельных осях .
Важно не путать момент инерции площади с массой момента инерции твердого тела. Момент инерции площади указывает на сопротивление поперечного сечения изгибу, тогда как момент инерции массы указывает на сопротивление тела вращению.
Теорема о параллельной оси
Если известен момент инерции поперечного сечения относительно центральной оси, то для вычисления момента инерции относительно любой параллельной оси можно использовать теорему о параллельных осях :
I параллельная ось = I c & plus; А д 2
где I c — момент инерции относительно центральной оси, d — расстояние между центральной осью и параллельной осью, а A — площадь поперечного сечения.
Если поперечное сечение состоит из набора основных форм, центроидные моменты инерции которых известны вместе с расстояниями центроидов до некоторой контрольной точки, то теорема о параллельных осях может использоваться для вычисления момента инерции составного поперечного сечения.
Например, двутавровая балка может быть аппроксимирована 3 прямоугольниками, как показано ниже. Поскольку это составное сечение симметрично относительно осей x и y, центр тяжести сечения можно определить путем осмотра на пересечении этих осей.Центроид расположен в начале координат O на рисунке.
Момент инерции составной секции можно рассчитать с помощью теоремы о параллельности осей. Центроидный момент инерции секции относительно оси x, I cx , рассчитывается как:
I cx.IBeam = I cx.W & plus; (I cx.F1 & plus; A F1 d 1 2 ) & plus; (I cx.F2 & plus; A F2 d 2 2 )
где члены I cx представляют собой моменты инерции отдельных секций относительно их собственных центроидов в ориентации оси x, члены d представляют собой расстояния от центроидов отдельных секций до центроидов составной секции, а Термины — это площади отдельных разделов.Поскольку центроид сечения W и центроид составного сечения совпадают, d для этого сечения равно нулю, поэтому член Ad 2 отсутствует.
Важно отметить, что из теоремы о параллельных осях следует, что по мере того, как отдельная секция перемещается дальше от центра тяжести составной секции, вклад этой секции в момент инерции составной секции увеличивается в d 2 . Следовательно, если намерение состоит в том, чтобы увеличить момент инерции секции относительно определенной оси, наиболее эффективно расположить область как можно дальше от этой оси.Это объясняет форму двутавровой балки. Фланцы вносят основной вклад в момент инерции, а перегородка служит для отделения фланцев от оси изгиба. Однако полотно должно сохранять некоторую толщину, чтобы избежать коробления и потому, что полотно принимает на себя значительную часть напряжения сдвига в сечении.
Полярный момент инерции
Полярный момент инерции , I, поперечного сечения является показателем способности конструктивного элемента противостоять скручиванию вокруг оси, перпендикулярной сечению.Полярный момент инерции для сечения относительно оси можно рассчитать следующим образом:
J = ∫ r 2 dA = ∫ (x 2 & plus; y 2 ) dA
где x и y — координаты элемента dA относительно интересующей оси, а r — расстояние между элементом dA и интересующей осью.
Хотя полярный момент инерции можно рассчитать с помощью приведенного выше уравнения, обычно удобнее рассчитывать его, используя теорему о перпендикулярной оси , которая гласит, что полярный момент инерции области является суммой моментов инерции относительно любые две ортогональные оси, проходящие через интересующую ось:
J = I x и плюс; Я y
Чаще всего интересующая ось проходит через центр тяжести поперечного сечения.
Модуль упругости сечения
Максимальное изгибающее напряжение в балке рассчитывается как σ b = Mc / I c , где c — расстояние от нейтральной оси до крайнего волокна, I c — центроидный момент инерции, а M — изгибающий момент. Модуль сечения объединяет члены c и I c в уравнении напряжения изгиба:
S = I c / c
Используя модуль упругости сечения, напряжение изгиба рассчитывается как σ b = M / S.Полезность модуля сечения заключается в том, что он характеризует сопротивление сечения изгибу одним термином. Это позволяет оптимизировать поперечное сечение балки, чтобы противостоять изгибу, за счет максимального увеличения одного параметра.
Радиус вращения
Радиус вращения представляет собой расстояние от центра тяжести секции, на котором вся площадь может быть сосредоточена без какого-либо влияния на момент инерции. Радиус вращения формы относительно каждой оси определяется как:
Полярный радиус вращения также может быть вычислен для задач, связанных с кручением вокруг центральной оси:
Прямоугольные радиусы вращения также можно использовать для вычисления полярного радиуса вращения:
r p 2 = r x 2 & plus; г г 2
Свойства общих сечений
В таблице ниже приведены свойства обычных поперечных сечений.Более подробные таблицы можно найти в перечисленных ссылках.
Свойства, вычисленные в таблице, включают площадь, центроидный момент инерции, модуль упругости сечения и радиус вращения.
Банкноты
Примечание 1: Прогиб балки
Прогиб балки при изгибе определяется моментом инерции поперечного сечения, длиной балки и модулем упругости материала.Более подробная информация представлена в этом обсуждении отклонения балки.
Список литературы
Гир, Джеймс М., «Механика материалов», 6-е изд.
Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена на физическую форму», 13-е изд.
Раздел 4 Закона об избирательных правах
Этот документ предназначен только для исторических целей. Министерство юстиции не будет использовать, цитировать или полагаться на этот документ, кроме как для установления исторического факта.Не следует ожидать, что информация, содержащаяся в этом документе, является актуальной или правильной.
Решение Верховного суда по делу Shelby County v. Holder, 570 US 529 (2013) постановило, что формула покрытия, изложенная в Разделе 4 (b) Закона, является неконституционной, и, как следствие, ни одна юрисдикция в настоящее время не распространяется формула в Разделе 4 (b) или в Разделах 4 (f) (4) и 5 Закона. Соответственно, информация о прекращении действия страхового покрытия в соответствии с разделом 4 (а) Закона об избирательных правах (т.e., bailout) некоторых специальных положений Закона больше не требуется. Информация о спасении в соответствии с Разделом 4 (а) и прошлых случаях спасения представлена здесь, на этой странице архива, в исторических целях.
Когда Конгресс принял Закон об избирательных правах 1965 года, он определил, что расовая дискриминация при голосовании была более распространена в некоторых районах страны. Раздел 4 (а) Закона устанавливает формулу для выявления этих областей и для обеспечения более строгих средств правовой защиты там, где это необходимо.Первым из этих целенаправленных средств правовой защиты была пятилетняя приостановка «теста или устройства», такого как проверка грамотности, в качестве предварительного условия для регистрации для голосования. Вторым было требование о пересмотре в соответствии с Разделом 5 любых изменений, влияющих на голосование в закрытой зоне, либо Окружным судом Соединенных Штатов округа Колумбия, либо Генеральным прокурором. Третий — это способность генерального прокурора удостоверить, что указанные юрисдикции также требуют назначения федеральных экспертов.Эти эксперты будут составлять и направлять списки лиц, имеющих право голоса. Последним средством правовой защиты в соответствии со специальными положениями является полномочие Генерального прокурора направлять федеральных наблюдателей в те юрисдикции, которые были сертифицированы для федеральных экспертов.
Раздел 4 также содержит несколько других положений, таких как Раздел 4 (e) и Раздел 4 (f), которые гарантируют право регистрации и голосования для лиц с ограниченным знанием английского языка. Раздел 4 (e) предусматривает, что в праве регистрации и голосования не может быть отказано тем лицам, которые закончили шестой класс в государственной школе, например, в Пуэрто-Рико, где преобладающим языком в классе является не английский язык.В Разделе 4 (f) Закона рассматривается возможность лиц, которые являются членами групп языковых меньшинств, указанных в Разделе 4 (f) (2), регистрироваться и голосовать, а также получать информацию, относящуюся к избирательному процессу в таким образом, который обеспечит их конструктивное участие в избирательном процессе.
В соответствии с постановлением 1965 года, первым элементом формулы было то, проводит ли 1 ноября 1964 года штат или политическое подразделение штата «тест или устройство», ограничивающее возможность регистрации и голосования.Определение «теста или устройства» в Законе включает такие требования, как возможность заявителя пройти тест на грамотность, установить, что он или она обладают хорошими моральными качествами, или иметь другого зарегистрированного избирателя, подтверждающего его или ее квалификацию.
Второй элемент формулы был бы удовлетворен, если бы директор переписи определил, что менее 50 процентов лиц избирательного возраста были зарегистрированы для голосования 1 ноября 1964 г. или что менее 50 процентов лиц избирательного возраста проголосовали в президентские выборы в ноябре 1964 г.Это привело к тому, что следующие штаты стали полностью «закрытыми юрисдикциями»: Алабама, Аляска, Джорджия, Луизиана, Миссисипи, Южная Каролина и Вирджиния. Кроме того, были охвачены определенные политические подразделения (обычно округа) в четырех других штатах (Аризона, Гавайи, Айдахо и Северная Каролина). В государствах с полным покрытием особые положения распространяются на само государство и все его политические подразделения. В «частично покрытых» штатах особые положения применяются только к определенным округам.Изменения при голосовании, принятые или подлежащие реализации в соответствующих политических подразделениях, включая изменения, применимые к штату в целом, подлежат рассмотрению в соответствии с Разделом 5.
В 1970 году Конгресс признал сохраняющуюся потребность в особых положениях Закона, срок действия которых истекал в этом году, и продлил их еще на пять лет. Он добавил второй компонент к формуле охвата, идентичный исходной формуле, за исключением того, что в нем указывалось, что ноябрь 1968 года является подходящей датой для обслуживания теста или устройства и уровней регистрации избирателей и участия в выборах.Это дополнение к формуле привело к частичному охвату десяти штатов, включая Аляску, Аризону, Калифорнию, Коннектикут, Айдахо, Мэн, Массачусетс, Нью-Гэмпшир, Нью-Йорк и Вайоминг. Половина из этих штатов (Коннектикут, Айдахо, Мэн, Массачусетс и Вайоминг) подали успешные судебные иски о «спасении».
В 1975 году специальные положения Закона были продлены еще на семь лет и были расширены, чтобы устранить дискриминацию при голосовании против членов «языковых меньшинств», которые были определены как лица, являющиеся индейцами Америки, американцами азиатского происхождения, коренными жителями Аляски или испанского происхождения. .«Как и прежде, Конгресс расширил формулу охвата, исходя из наличия тестов или устройств и уровней регистрации и участия избирателей по состоянию на ноябрь 1972 года. Кроме того, определение 1965 года« тест или устройство »было расширено, чтобы включить практику предоставления любая информация о выборах, включая бюллетени, только на английском языке в штатах или политических единицах, где члены одноязычного меньшинства составляли более пяти процентов граждан избирательного возраста. Этот третий компонент формулы охвата имел эффект охвата Аляски, Аризона, и Техас в целом, а также части Калифорнии, Флориды, Мичигана, Нью-Йорка, Северной Каролины и Южной Дакоты.
В 1982 году формула покрытия была снова расширена, на этот раз на 25 лет, но никаких изменений в нее не было. В 2006 году формула покрытия была снова продлена на 25 лет.
Раздел 4 также предусматривает, что юрисдикция может прекратить или «спасти» покрытие согласно особым положениям Закона. Первоначально принятый в 1965 году как средство устранения любой возможной чрезмерной инклюзивности, возникающей в результате применения триггерной формулы, Конгресс внес поправки в эту процедуру в 1982 году, чтобы юрисдикции, соответствующие законодательным стандартам, могли получить компенсацию.Поправка, вступившая в силу 5 августа 1984 г., устанавливает «объективную» меру для определения того, имеет ли юрисдикция право на «спасение».
Юрисдикция, претендующая на «спасение», должна запросить декларативное решение от коллегии из трех судей Окружного суда США округа Колумбия. 22 июня 2009 г. Верховный суд постановил, что любая юрисдикция, которая в настоящее время требуется для подачи заявлений по Разделу 5, может стремиться к «спасению» от покрытия, если оно соответствует установленным законом критериям, изложенным ниже.
Успешный соискатель «помощи» должен продемонстрировать, что за последние десять лет:
- Никакие испытания или устройства не использовались в пределах юрисдикции с целью или с целью дискриминации при голосовании;
- Все изменения, влияющие на голосование, были рассмотрены в соответствии с Разделом 5 до их внедрения;
- Никакие изменения, влияющие на голосование, не были предметом возражений со стороны Генерального прокурора или отклонения декларативного решения по Разделу 5 окружного суда округа Колумбия;
- По искам о дискриминации при голосовании не было вынесено отрицательных судебных решений;
- Не было никаких указов или соглашений о согласии, которые привели бы к отказу от дискриминационной практики голосования;
- Нет ожидающих рассмотрения судебных исков о дискриминации при голосовании; и
- федеральных экспертов;
- Не было никаких нарушений Конституции или федеральных, государственных или местных законов в отношении избирательной дискриминации, если только юрисдикция не установила, что любые такие нарушения были незначительными, были незамедлительно исправлены и не повторялись.
Не назначено
Прежде чем получить разрешение на «спасение», юрисдикция должна отменить те процедуры голосования и методы выборов, которые препятствуют или ослабляют равный доступ к избирательному процессу. Он также должен продемонстрировать, что он предпринял конструктивные усилия для устранения запугивания и преследования лиц, желающих зарегистрироваться и проголосовать, и расширить возможности для участия избирателей, такие как возможности для регистрации и голосования, а также для назначения должностных лиц меньшинств по всей юрисдикции и на всех уровнях этапы избирательного процесса.Судебная инстанция также должна представить доказательства участия меньшинства в выборах.
Кроме того, эти требования применяются ко всем государственным единицам в пределах географических границ юрисдикции. Таким образом, если округ стремится к «спасению», он должен установить каждый критерий для каждого города, поселка, школьного округа или другого субъекта в его границах.
Юрисдикция, ищущая «спасение», должна предать гласности предполагаемое начало и любое предлагаемое урегулирование иска; любая потерпевшая сторона может вмешаться в судебный процесс.После вынесения декларативного решения статут требует десятилетнего периода «повторного захвата». В течение этого времени окружной суд может возобновить разбирательство, если юрисдикция совершит какое-либо поведение, которое помешало бы юрисдикции спасти дело в первой инстанции. При таких обстоятельствах окружной суд рассмотрит доказательства и определит, следует ли восстановить страховое покрытие.
Генеральный прокурор также уполномочен дать согласие на внесение судебного решения о предоставлении «финансовой помощи», если Генеральный прокурор после расследования придет к выводу, что юрисдикция выполнила все эти требования.Перед фактической подачей петиции в суд округа Колумбия любая юрисдикция, заинтересованная в поиске «финансовой помощи», может подать запрос Генеральному прокурору с подтверждающими документами и доказательствами. После его получения Отдел голосования Отдела гражданских прав проведет расследование, чтобы определить, захочет ли Генеральный прокурор подписать указ о согласии или выступит против ходатайства о «финансовой помощи». Если Генеральный прокурор определит, что согласие на внесение судебного решения является надлежащим, Секция голосования будет работать с юрисдикцией, чтобы согласовать условия постановления о согласии, которое должно быть подано с ходатайством о «спасении», когда судебный процесс фактически подан.
Следующие ниже юрисдикции когда-то подпадали под действие Раздела 5 Закона об избирательных правах, но успешно получили декларативное решение в соответствии с Разделом 4 Закона об избирательных правах и в настоящее время спасены. Дата, указанная ниже, является датой, когда этим юрисдикциям было вынесено декларативное судебное решение, разрешающее им выручить. Также ниже приведены некоторые примеры изложения фактов и постановления о согласии в нескольких случаях оказания финансовой помощи.
Округ Уэйк, Северная Каролина — 23 января 1967 г.
Карри, округа Мак-Кинли и Отеро, Нью-Мексико — 30 июля 1976 г.
Города Кэдвелл, Известняк, Ладлоу, Нэшвилл, Рид, Вудленд, Коннор, Нью-Глостер, Салливан, Уинтер-Харбор, Челси, Соммервилл, Кэрролл, Чарльстон, Вебстер, Уолдо, Беддингтон и Катлер, Мэн — 17 сентября 1976 г.
округа Чокто и Мак-Кертейн, Оклахома — 12 мая 1978 г.
Кэмпбелл Каунти, Вайоминг — 17 декабря 1982 г.
Города Амхерст, Эйер, Белчертаун, Борн, Гарвард, Сэндвич, Ширли, Сандерленд и Рентам, Массачусетс — 29 сентября 1983 г.
Города Гротон, Мэнсфилд и Саутбери, Коннектикут — 21 июня 1984 г.
Округ Эль-Пасо, Колорадо — 30 июля 1984 г.
Округ Гонолулу, Гавайи — 31 июля 1984 г.
округ Элмор, штат Айдахо — 22 сентября 1966 года; 31 июля 1984 г.
Город Фэрфакс, штат Вирджиния, включая школьный совет города Фэрфакс — 21 октября 1997 г.
Постановление о согласии с фактами
округа Фредерик, штат Вирджиния, включая школьный совет округа Фредерик, города Мидлтаун и Стивенс-Сити; и Санитарный округ округа Фредерик Шоунилэнд — 9 сентября 1999 г., Указ №
о согласовании фактов
Округ Шенандоа, Вирджиния, включая школьный совет округа Шенандоа, города Эдинбург, гору Джексон, Нью-Маркет, Страсбург, Томс-Брук и Вудсток, санитарный район Стони-Крик и санитарный район Томс-Брук-Маурертаун — 15 октября 1999 г.
Постановление о согласии с фактами
Округ Роанок, Вирджиния, включая школьный совет округа Роанок и город Винтон — 24 января 2001 г.
Постановление о предоставлении согласия
Город Винчестер, Вирджиния — 1 июня 2001 г.
Указ о согласовании фактов
Город Харрисонбург, штат Вирджиния, включая школьный совет города Харрисонбург — 17 апреля 2002 г.
Постановление о предоставлении согласия
округа Рокингем, штат Вирджиния, включая школьный совет округа Рокингем и города Бриджуотер, Бродвей, Дейтон, Элктон, Гроттоз, Маунт.Кроуфорд и Тимбервилль — 24 мая 2002 г., постановление №
о согласовании фактов
Округ Уоррен, штат Вирджиния, включая школьный совет округа Уоррен и муниципалитет Фронт-Роял — 26 ноября 2002 г.
Постановление о согласии с фактами
Графство Грин, Вирджиния, включая школьный совет графства Грин и город Стандардсвилл — 19 января 2004 г.
Указ о согласовании фактов
Округ Пуласки, Вирджиния, включая Школьный совет округа Пуласки и города Пуласки и Дублин — 27 сентября 2005 г.
Указ о согласовании фактов
Округ Огаста, штат Вирджиния, включая школьный совет округа Огаста и город Крейгсвилл — 30 ноября 2005 г.
Указ о согласовании фактов
Город Салем, Вирджиния — 27 июля 2006 г.
Указ о согласовании фактов
Округ Боттурт, штат Вирджиния, включая школьный совет округа Боттурт и города Бьюкенен, Финкасл и Траутвилл — 28 августа 2006 г.
Указ о согласовании фактов
Округ Эссекс, штат Вирджиния, включая Школьный совет графства Эссекс и город Таппаханнок — 31 января 2007 г.
Условия предоставления фактов (1) Условия предоставления фактов (2) Указ о согласии
Округ Миддлсекс, штат Вирджиния, включая школьный совет округа Мидлсекс и город Урбанна — 7 января 2008 г.
Постановление о предоставлении согласия
Округ Амхерст, Вирджиния, включая город Амхерст — 13 августа 2008 г.
Указ о согласовании фактов
Округ Пейдж, Вирджиния, включая школьный совет округа Пейдж и города Лурей, Стэнли и Шенандоа — 15 сентября 2008 г.
Постановление о предоставлении согласия
Округ Вашингтон, Вирджиния, включая школьный совет округа Вашингтон и города Абингтон, Дамаск и Глэйд-Спринг — 23 сентября 2008 г.
Северо-западный муниципальный район Остина номер один, Техас — 3 ноября 2009 г.
Город Кингс-Маунтин, Северная Каролина — 22 октября 2010 г.
Указ о согласии
Город Сэнди-Спрингс, Джорджия — 26 октября 2010 г.
Указ о согласии
Дренажный округ округа Джефферсон номер семь, Техас — 6 июня 2011 г.
Указ о согласии
Алтинский ирригационный округ, Калифорния — 15 июля 2011 г.
Указ о согласии
Городской парк Манассас, штат Вирджиния — 3 августа 2011 г.
Указ о согласии
Округ Раппаханнок, штат Вирджиния, включая школьный совет округа Раппаханнок и город Вашингтон — 9 августа 2011 г.
Указ о согласии
Округ Бедфорд, штат Вирджиния, включая школьный совет округа Бедфорд — 30 августа 2011 г.
Указ о согласии
Город Бедфорд, штат Вирджиния — 31 августа 2011 г.
Указ о согласии
Округ Калпепер, штат Вирджиния, включая школьный совет округа Калпепер и город Калпепер — 3 октября 2011 г.
Указ о согласии
Округ Джеймс-Сити, штат Вирджиния — 9 ноября 2011 г.
Указ о согласии
Город Вильямсбург, штат Вирджиния, включая школьный совет округа Вильямсбург-Джеймс — 28 ноября 2011 г.
Указ о согласии
Округ Кинг-Джордж, штат Вирджиния, включая школьный совет округа Кинг-Джордж — 5 апреля 2012 г.
Указ о согласии
Округ Принц Уильям, штат Вирджиния, включая школьный совет округа Принц Уильям и города Дамфрис, Хеймаркет, Оккокван и Квантико — 10 апреля 2012 г.
Указ о согласии
Город Пинсон, Алабама — 20 апреля 2012 г.
Указ о согласии
Округ Уайт, штат Вирджиния, включая школьный совет округа, а также городки в сельской местности и Уайтвилле — 18 июня 2012 г.
Указ о согласии
Округ Грейсон, штат Вирджиния, включая школьный совет графства и города Независимости, Фрайс и Траутдейл — 20 июля 2012 г.
Указ о согласии
Округ Мерсед, Калифорния, включая около 84 других государственных единиц — 31 августа 2012 г.
Указ о согласии
Округ Крейг, штат Вирджиния, включая школьный округ округа Крейг и город Нью-Касл — 29 ноября 2012 г.
Указ о согласии
Округ Кэрролл, штат Вирджиния, включая школьный округ округа Кэрролл и город Хиллсвилл — 30 ноября 2012 г.
Указ о согласии
Ирригационный район Браунс-Вэлли в округе Юба, Калифорния — 4 февраля 2013 г.
Указ о согласии
Города Антрим, Бентон, Боскавен, Миллсфилд, Ньюингтон, Пинкхэм-Грант, Риндж, Стюартстаун, Стратфорд и Юнити, Нью-Гэмпшир — 1 марта 2013 г.
Указ о согласии
Город Уитленд в округе Юба, Калифорния — 25 апреля 2013 г.
Указ о согласии
Город Фоллс-Черч, штат Вирджиния, и муниципальный школьный округ города Фоллс-Черч — 29 мая 2013 г.
Указ о согласии
Расчет статического / первого момента площади
размер шрифта: 15 пикселей;
}
]]>
Как рассчитать статический или первый момент площади сечения балки?
Статический или первый момент площади (Q) просто измеряет распределение площади сечения балки относительно оси.Он рассчитывается путем суммирования всех площадей, умноженных на их расстояние от конкретной оси (Площадь на расстояние).
На самом деле, возможно, вы этого не осознавали, но если вы вычислили центроид сечения балки, вы бы уже вычислили первый момент площади. Кроме того, это свойство, часто обозначаемое Q, чаще всего используется при определении напряжения сдвига сечения балки.
Поскольку секции балки обычно состоят из множества геометрических фигур, сначала необходимо разделить секцию на сегменты.После этого, чтобы найти общий статический момент площади, вычисляются площадь и центроид каждого сегмента.
Рассмотрим сечение двутавровой балки, показанное ниже. В нашем предыдущем уроке мы уже обнаружили, что центр тяжести находится на расстоянии 216,29 мм от нижней части секции. Чтобы вычислить статический момент площади относительно горизонтальной оси x, сечение можно разделить на 4 сегмента, как показано на рисунке:
Помните, что первый момент площади — это сумма площадей, умноженная на расстояние от оси.Таким образом, формула для статического момента площади относительно горизонтальной оси x:
Теперь для такого результата, как напряжение сдвига, нам часто нужен статический момент ВЕРХНЕЙ или НИЖНЕЙ части сечения относительно нейтральной оси (NA) XX. Начнем с ВЕРХНЕЙ части раздела (то есть с сегментов 1 и 2).
Найдем A i и y i для каждого сегмента двутаврового сечения над нейтральной осью, а затем вычислим статический момент площади (Q x ).Помните, что мы измеряем расстояния от нейтральной оси!
Аналогичным образом мы можем вычислить статический момент площади НИЖНЕЙ части сечения. Это касается сегментов 3 и 4, которые находятся ниже нейтральной оси.
Вы заметите, что статический момент области над нейтральной осью равен моменту под нейтральной осью!
[математика]
{Q} _ {x, вверху} = {Q} _ {x, bottom}
[математика]
Конечно, вам не нужно делать все эти расчеты вручную.Вы можете использовать наш фантастический калькулятор свободного момента инерции, чтобы определить статический момент площади секций балки.
Калькулятор свободного момента инерции
Посетите следующий шаг: Как рассчитать момент инерции секции балки.
грантов по формуле урбанизированных территорий — 5307
Что нового
Национальный центр прикладных транзитных технологий (N-CATT) предоставляет экспертную и целенаправленную техническую помощь транспортным агентствам и организациям в сельских районах и малых городах в использовании или разработке транзитных технологий и инноваций, которые делают услуги более рентабельными и эффективными.Работа N-CATT поддерживает миссию FTA и фокусируется на инновациях путем разработки и поддержки транзитных программ и услуг в сельских и малых городах Америки.
Обзор программы
Программа финансирования по формуле урбанизированных территорий (49 U.S.C.5307) предоставляет федеральные ресурсы городским районам и губернаторам для транзитного капитала и оперативной помощи в урбанизированных районах, а также для планирования, связанного с транспортом. Урбанизированная территория — это объединенная территория с населением 50 000 или более человек, обозначенная как таковая U.S. Министерство торговли, Бюро переписи населения.
Доли
- FY 2019: 5 262 516 268
- FY 2018: 5,137,177,613
- 2017 финансовый год: 5 010 807 790
- FY 2016: 4 911 077 833
- FY 2015: 4 823 914 787
Правомочные получатели
Финансирование предоставляется назначенным получателям, которые являются государственными органами с законными полномочиями получать и распределять федеральные средства. Губернаторы, ответственные местные должностные лица и государственные операторы транзитных услуг должны назначить получателя для подачи заявки, получения и распределения средств для урбанизированных территорий в соответствии с 49USCA5307 (a) (2).Губернатор или назначенный губернатор выступает в качестве назначенного получателя для урбанизированных районов от 50 000 до 200 000 человек.
Для урбанизированных районов с населением 200 000 человек и более средства распределяются и поступают непосредственно назначенному получателю, выбранному на местном уровне для подачи заявки и получения федеральных средств. Для урбанизированных районов с населением менее 200 000 человек средства распределяются между губернаторами каждого штата.
Допустимые мероприятия
Приемлемые виды деятельности включают: планирование, проектирование, проектирование и оценку транзитных проектов и другие технические исследования, связанные с транспортировкой; капитальные вложения в автобусную и связанную с автобусами деятельность, такую как замена, капитальный ремонт и восстановление автобусов, оборудование для предотвращения преступности и безопасности, а также строительство объектов технического обслуживания и пассажиров; и капитальные вложения в новые и существующие системы фиксированных направляющих, включая подвижной состав, капитальный ремонт и реконструкцию транспортных средств, путей, сигналов, средств связи, компьютерного оборудования и программного обеспечения.Кроме того, соответствующая модернизация транспорта и определенные расходы, связанные с программами управления мобильностью, имеют право на участие в программе. Все затраты на профилактическое обслуживание и некоторые дополнительные услуги паратранзита согласно Закону об американцах с ограниченными возможностями считаются капитальными затратами.
Для урбанизированных районов с населением менее 200 000 человек эксплуатационная помощь является приемлемым расходом. Урбанизированные районы с населением 200 000 и более не могут использовать средства для оказания операционной помощи, если только они не определены FTA как отвечающие требованиям Специального правила.
Нормативная ссылка
49 U.S.C. 5307
Доступность финансирования
Средства доступны в течение выделенного года плюс пять лет.
Распределение финансирования
Финансирование распределяется на основании законодательных формул. Для районов с населением от 50 000 до 199 999 человек формула основана на численности населения и плотности населения. Для районов с населением 200 000 человек и более формула основана на комбинации миль для коммерческих автобусов, пассажирских миль для автобусов, миль для коммерческих транспортных средств с фиксированными направляющими и миль для фиксированных направляющих маршрутов, а также на численности населения и плотности населения.
Посмотрите формулу пропорционального распределения 5307 на 2019 финансовый год.
Матч
Доля федерального бюджета не должна превышать 80 процентов чистой стоимости проекта по капитальным затратам. Федеральная доля может составлять 90 процентов от стоимости оборудования, связанного с транспортными средствами, в связи с соблюдением Закона об американцах с ограниченными возможностями и Закона о чистом воздухе. Доля федерального бюджета не может превышать 50 процентов чистой стоимости проекта по операционному содействию.
6.1.1: Сечение столкновений — Chemistry LibreTexts
Сечение столкновений — это «эффективная площадь», которая количественно определяет вероятность события рассеяния, когда случайный вид поражает целевой вид. В приближении твердого объекта поперечное сечение — это площадь обычного геометрического поперечного сечения. Сечения столкновения обычно обозначаются σ и измеряются в единицах площади.
Введение
Атомы и молекулы могут перемещаться в пространстве и сталкиваться друг с другом.При соблюдении определенных условий столкновения происходит химическая реакция и образуется продукт. Однако иногда частицы могут подбираться очень близко друг к другу, но не ударяются. Мы можем использовать сечение столкновения, чтобы определить, насколько большим должно быть расстояние между двумя частицами, чтобы произошло столкновение.
Необходимо сделать несколько предположений:
- Все частицы движутся в пространстве линейно
- Все частицы представляют собой твердые сферы
- В столкновении участвуют только две частицы
Сечение столкновения определяется как область вокруг частицы, в которой должен находиться центр другой частицы, чтобы произошло столкновение.2} \]
Столкновение происходит, когда расстояние между центрами двух молекул реагента меньше суммы радиусов этих молекул, как показано на рисунке \ (\ PageIndex {2} \). Сечение столкновения описывает область вокруг единственного реагента. Для возникновения реакции столкновения центр одного реагента должен находиться в пределах поперечного сечения столкновения соответствующего реагента.
Рисунок \ (\ PageIndex {2} \): Расстояние меньше, чем радиусы \ (A \) и \ (B \), поэтому столкновения не происходит.2 \ nonumber \]
Хотя сечение столкновения частицы можно вычислить, оно обычно не используется само по себе (Таблица \ (\ PageIndex {1} \)). Вместо этого это компонент более сложных теорий, таких как частота столкновений и теория столкновений.
| Молекула | Поперечное сечение (нм 2 ) |
|---|---|
| Ар | 0.36 |
| C 2 H 4 | 0,64 |
| C 6 H 6 | 0,88 |
| Канал 4 | 0,46 |
| Класс 2 | 0,93 |
| CO 2 | 0,52 |
| H 2 | 0,27 |
| He | 0.21 |
| N 2 | 0,43 |
| Ne | 0,24 |
| О 2 | 0,40 |
| СО 2 | 0,58 |
А что, если бы частицы были разного размера и радиуса? Член \ (2r \) в уравнении \ (\ ref {SameEq} \) на самом деле является суммой радиуса каждой молекулы (то есть \ (2r = r + r \)). Однако, если сталкивающиеся молекулы имеют разные размеры (например,2 \]
Сектор круга и сегмент
Ломтики
Есть два основных «кусочка» круга:
- Кусочек «пиццы» называется Сектор .
- И Сегмент , который вырезан из круга «хордой» (линия между двумя точками на окружности).
Попробуйте!
Общие сектора
Квадрант и Полукруг — это два особых типа сектора:
Полукруг — это
полукруг .
Четверть круга — это
квадрант .
Площадь сектора
Вы можете определить площадь сектора, сравнив его угол с углом полного круга.
Примечание: мы используем радианы для углов.
Это рассуждение:
Круг имеет угол 2π и площадь: πr 2
Сектор имеет угол θ вместо 2π, поэтому его площадь составляет: θ 2π × πr 2
Что можно упростить до: θ 2 × r 2
Площадь сектора =
θ
2
× r 2 (когда θ в радианах)
Площадь сектора =
θ × π
360
× r 2 (когда θ в градусах)
Площадь участка
Площадь сегмента — это площадь сектора за вычетом треугольной части (здесь показана голубым цветом).
Есть длинная причина, но результатом является небольшая модификация формулы Сектора:
Площадь сегмента =
θ — грех (θ)
2
× r 2 (когда θ в радианах)
Площадь сегмента = (
θ × π
360
— sin (θ) 2
) × r 2 (когда θ в градусах)
Длина дуги
Длина дуги (сектора или сегмента ) составляет:
L = θ × r (когда θ в радианах)
L = θ × π 180 × r (когда θ в градусах)
У меня возникла ошибка Проверка> Анализ> Общие> «Недопустимая область раздела».Почему я получаю это и как мне это разрешить?
Последнее обновление 28 марта 2021 г. от
Команда разработчиков Tekla Structural Designer
[email protected]
Вопрос
У меня есть ошибка Проверка> Анализ> Общие> «Недопустимая область раздела ». Почему я получаю это и как мне это разрешить?
Ответ
Чтобы получить эту ошибку проверки, вы должны создать свой собственный определяемый пользователем раздел в базе данных сечения материалов, но неправильно определили свойство площади поперечного сечения, а затем впоследствии использовали сечение в модели.После анализа отобразится ошибка проверки.
Если мы наведем курсор на область Раздел недействителен, ошибка проверки или элемент, указанный в ветке, отобразится всплывающая подсказка « Член имеет недопустимую или нулевую область ».
Мы можем дважды щелкнуть ошибку « Область раздела недействительна » или отдельный элемент, указанный в ветке. Если элементы существуют в активном представлении, они будут выделены. Если их нет на активном виде, Tekla Structural Designer автоматически переключится на вид 3D-структуры и выделит элемент (ы).Кроме того, вы можете щелкнуть правой кнопкой мыши и выбрать Highlight Items из контекстного меню. Выбранные элементы также отображаются в окне свойств для просмотра и редактирования.
Вы можете использовать Scene Content и выключить такие элементы, как панели Wall и Roof, чтобы уменьшить беспорядок в обзоре.
Хотя вы можете просматривать и редактировать некоторые свойства в окне Свойства , Редактировать свойства пользовательского сечения материала невозможно.Однако мы можем ясно видеть недопустимую запись для площади поперечного сечения.
Чтобы исправить ошибку проверки, нам нужно использовать вкладку на главной ленте> команду «Материалы », чтобы иметь возможность Редактировать раздел. (См. Снимок экрана ниже).
Вы можете найти соответствующую статью « Как создать настраиваемый раздел ».
Доступна кнопка Edit… , с помощью которой мы можем исправить неверное свойство раздела.