Теплопроводность схема: 404 — Ошибка: 404

Теплопроводность пенопласта: цифры, факты и схемы

Все о ней говорят, но никто не видел. Разумеют, что она нужна, а где взять, не знают. Понимают, что надо её понижать, но как, не ведают. Ведь разговор идет о способности утеплителя не допускать передачу тепловой энергии через занятую им площадь, а проще говоря, о его низкой теплопроводности. Теплопроводность пенопласта является основной характеристикой, определяющей порядок его использования в утеплении зданий и сооружений.

Основа низкой теплопроводности

Всем своим имеющимся положительным и отрицательным свойствам, пенопласт (вспененный пенополистирол) обязан стиролу и особой технологии производства.

Вначале стирол насыщают газом или воздухом, превращая в пустотелые гранулы. Затем под воздействием горячего пара происходит многократное увеличение объёма гранул с последующим спеканием их при наличии связующего состава. Таким образом, получаемый лист состоит из множества сфер правильной формы, наполненных газом.

Стирольные стенки тонкие, но очень прочные. Даже при приложении значительных усилий, разрушить оболочку не так уж и просто. Удерживаемый внутри газ остается неподвижным при любых условиях эксплуатации, обеспечивая высокую тепловую изоляцию защищаемого объёма.

Наполнение объёма утеплителя газами зависит от его плотности. Меняется от 93 до 98 %. Чем больше процент, тем меньше плотность, тем легче материал, тем выше теплопроводность, и обычно выше качество утепления и другие важные характеристики.

Вникаем в смысл понятия

Понять смысл «теплопроводность пенополистирола» можно через физическую размерность. Измеряется данная величина в Вт/м ч К. Расшифровать её можно следующим образом: сколько ватт тепловой энергии пройдёт через толщину утеплителя площадью 1 м2 в час при снижении температуры нагретой поверхности на 1 К (Кельвин). 1 К равен 1^оС.

Схема утечки тепла через утеплитель

В технических характеристиках материала разной плотности указывается коэффициент теплопроводности пенопласта. Он колеблется в диапазоне от 0,032 до 0,04 единицы. При увеличении плотности плиты это значение уменьшается.

Теплопроводность простыми словами: сколько ватт тепловой энергии пройдёт через толщину утеплителя площадью 1 м2 в час при снижении температуры нагретой поверхности на 1 К (Кельвин). 1 К равен 1^оС.

Но бесконечно повышая плотность материала, невозможно добиться нулевых теплопотерь. Перейдя некоторую границу и продолжая увеличивать плотность, получим скачкообразный рост потери тепла. Необходимо понимание того, что при увеличении плотности, объём и количество газа в материале сокращаются, и как следствие, термоизоляция ухудшается.

Опытным путём установлено, что максимальная способность изолятора удерживать тепло достигается при его плотности от 8 до 35 кг/м3. Это число, указанное на упаковке, показывает, сколько весит 1 м3 утеплителя при заявленной плотности. Малая плотность – малый вес. Малый вес – удобство монтажа и укладки.

Всё тоньше, всё теплее

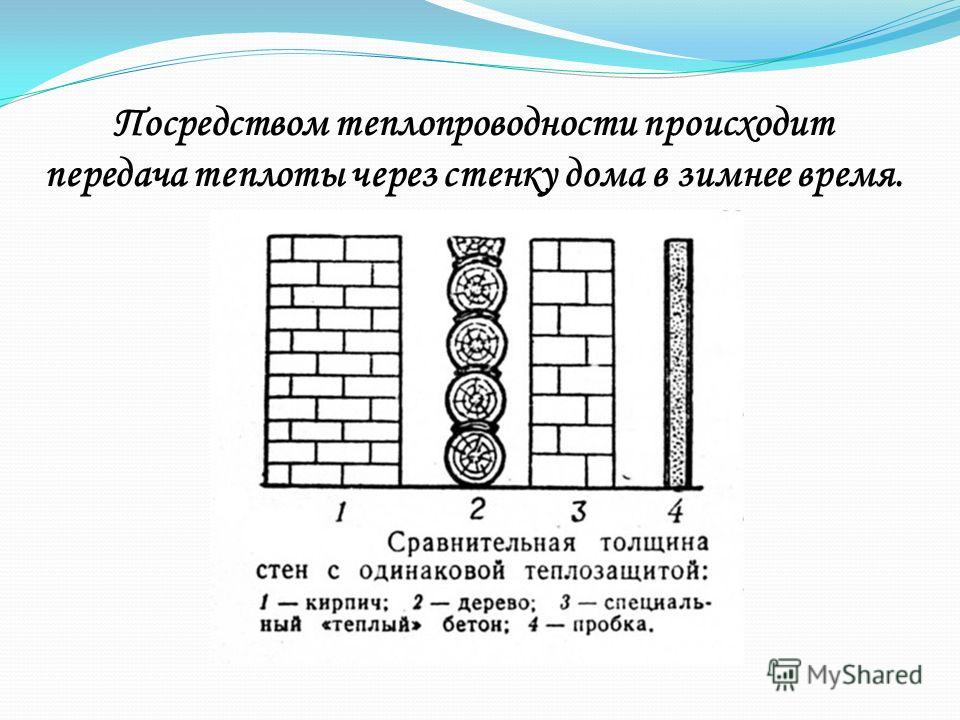
Для того чтобы представить эту физическую величину наглядно, проведём сравнение теплопроводности пенопласта с другими строительными материалами. Представьте, что вы стоите и смотрите с торца на разрезы стен из разных материалов. Сначала перед глазами проплывает бетонная стена толщиной 3,2 м, затем кирпичная кладка в 5 кирпичей (1,25 м), потом относительно тоненькая деревянная перегородка шириной с предплечье взрослого человека (0,40 м). И уже где-то в самом конце, незаметный лист пенопласта толщиной 0,1 м. Что же объединяет все эти материалы необъятной толщины? Только одно.

У них одинаковый коэффициент удельной теплопроводности.

Используя его низкую теплопроводимость, можно в значительной степени сократить расход достаточно дорогих в приобретении и укладке стройматериалов. Дом, построенный в 2,5 кирпича так же надёжен, как и дом с толщиной стен в 5 кирпичей. Только в первом случае расходы на отопление больше. Хотите дом теплее? Не надо возводить ещё такую же стену. Достаточно утеплить стену 50 мм плитой. Почувствуйте разницу. 2,5 кирпича по периметру дома и лист пенопласта толщиной в 50 мм. Экономим время, деньги, силы.

Трудность выбора

Кто-то может возразить, что это некорректное сравнение. Нельзя сравнивать материалы, настолько разные по своему происхождения и внутреннему составу. Хорошо. Тогда сравним современные утеплители: минеральные (базальтовые), вспененный и экструдированный пенополистиролы, пенополиуретан.

Проводимое сравнение явно не в пользу плит и матов из волокнистых материалов. Их теплоёмкость почти в 1,5 раза больше, чем у пенопласта. Это сразу понижает их потребительскую ценность и ставит на нижнюю степень по этому показателю.

Сравнить теплопроводность экструдированного пенополистирола и пенопласта достаточно затруднительно. Физически и математически показатели очень близки. Признавая лидерство, имеющего более низкий коэффициент теплопроводности экструдированного пенополистирола, вспененный полистирол отвечает ему своим преимуществом – ценой. Разницу в 4 сотых единицы указанного коэффициента, вспененный полистирол перекрывает ценой, которая в 4 раза ниже, чем у именитых конкурентов.

Даже при сравнении теплопроводности пенополиуретана и пенопласта можно сказать о том, что вспененный пенополистирол «хорошо держит удар». Коэффициент теплопроводности пенополиуретана только на 30% меньше, чем у вспененного полистирола. А цена… Не стоит забывать о том, что его монтаж требует определённой квалификации, оборудования. Что потребует дополнительных затрат. Утепление дома пенопластом можно провести своими руками.

Так что есть над чем поразмышлять, прежде чем сделать выбор утеплителя.

Применяем, ориентируясь на числа

Именно коэффициент теплопроводности пенополистирола определяет порядок и место его применения.

Материал с невысокой плотностью и высокой теплопроводностью применяется для утепления вертикальных конструкций внутри помещений.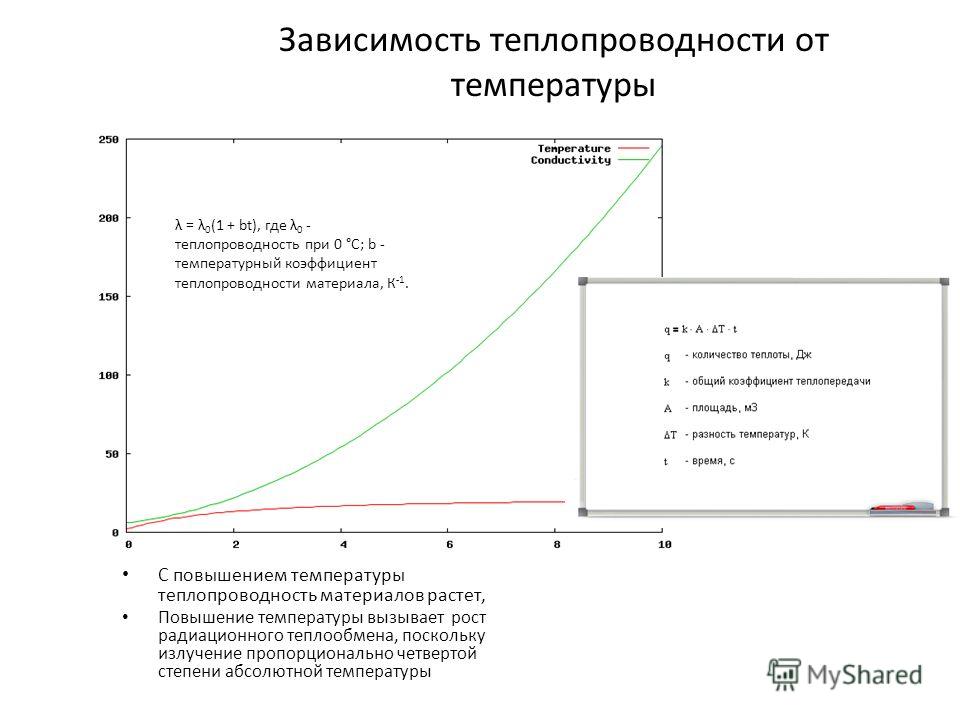 Это пенополистиролы с числом «15» в маркировке. Они имеют небольшую толщину и не сильно поглощают внутренние объёмы.

Утеплитель, обозначенный числом «25», имеет возможность использования при наружном утеплении стен, межэтажных (чердачных, подвальных) перекрытий, скатных и плоских кровель, как частных домовладений, так и многоэтажных строений.

Самую высокую плотность и самое низкое значение удельной теплопроводности имеют пенопласты с числом «35» в наименовании. Они достойно утепляют заглубленные фундаменты, автомобильные дороги, взлётно-посадочные полосы.

Наверное, нет такого строительного материала, который не мог бы утеплить пенопласт. Если невозможно увидеть его высокую термоизоляции, это не значит, что её нет. В этом можно убедиться после утепления дома, получив счёт за потреблённые энергоресурсы.

Теплотехнический расчет нестандартного железобетонного сечения в условии пожара с применением модуля «Теплопроводность» ПК Лира-САПР

Исследуемая конструкция: монолитная железобетонная плита из тяжелого бетона В25, армированная снизу стержневой арматурой диаметром 12 мм класса А500 и сверху стержневой арматурой диаметром 8 мм класса А500 с шагом 187.5 мм, выполненная на профилированном настиле Н75-750-0.8. Величина защитного слоя для нижней арматуры — 35 мм, для верхней — 28 мм. Сечение плиты представлено на рисунке 1.

Рис. 1

Подготовленный контур плиты (без арматурных стержней и аннотаций) сохраняем в формате dxf 2013 года. Открываем ПК ЛИРА-САПР и создаем новую задачу теплопроводности (признак схемы — 15). Импортируем подготовленную подложку (значок ПК ЛИРА-САПР вверху слева и далее Импортировать задачу — dxf файлы). Импортированный контур представляет собой набор узлов, соединенных стержнями. Для последующего расчета необходимо выполнить триангуляцию контура (см. рис. 2 и 3).

Рис. 2

Указываем в появившемся окне параметры согласно рисунку 3, и поэтапно указываем все узлы (закончить указание узлов нужно в начальном узле).

Рис. 3

После того как были указаны все узлы, контур примет синий цвет. Подтвердим триангуляцию контура нажав на зеленую галочку. Триангуляция контура завершена, см. рисунок 4.

Рис. 4

Теперь создадим жесткость для созданных пластин. Открываем инструмент Жесткости на панели Схема и нажимаем Добавить. В открывшемся окне двойным щелчком выбираем Теплопроводность (пластины) и далее вводим параметры согласно рисунку 5. Коэффициенты теплопроводности и теплоемкости посчитаны для температуры 300 С, для лучшего соответствия результатам номограмм СТО 36554501-006-2006.

Рис. 5

После создания жесткости необходимо её применить пластинам. Для этого удобно воспользоваться Полифильтром. На панели инструментов внизу окна выбираем Полифильтр, переходим на вторую вкладку, ставим галочку у списка «По виду КЭ» и далее выбираем в списке Пластины. Подтверждаем выбор элементов на заданным параметрам нажатием зеленой галочки. См. рисунок 6. Выбранные пластины будут подсвечены красным цветом. Теперь открываем окно Жесткостей (панель Схема), два раза щелкаем по созданной ранее жесткости (Теплопроводность (пластины) – Бетон) и нажимаем зеленую галочку справа от строки Жесткость. Выбранным пластинам назначена жесткость.

Рис. 6

Удалим за ненадобностью стержни вдоль верхней и боковых граней сечения плиты. См. рисунок 7.

Рис. 7

Следующим этапом создадим в каждом узле сечения нагрузку в виде начальной температуры в 20 градусов по Цельсию. Для этого выбираем все узлы на схеме и нажимаем на инструмент Нагрузки на одноименной панели. На вкладке Нагрузки в узлах выбираем Заданная температура, в качестве параметра которой указываем значение 20. См. рисунок 8. Подтверждаем создание нажатием зеленой галочки.

Рис. 8

Создадим также еще 7 загружений. 2-5 останутся пустыми, 6-ая будет задействована под конвекцию, 7-ая — под лучистый теплообмен (радиацию). Создать загружения можно путем нажатия стрелки вверх (6 раз) на нижней панели выбора загружений.

Укажем для схемы, с какой стороны происходит нагрев. Для этого выделяем на схеме только стержни по нижней грани сечения. Это можно выполнить как с помощью Полифильтра, так и с помощью нажатия двух инструментов на панели внизу окна (см. рисунок 9). После выделения стержней выполним их фрагментацию на схеме.

Рис. 9

Изменим тип конечных элементов стержней на тип 1555. Указав нужный тип в списке и нажав зеленую галочку. См. рисунок 10.

Рис. 10

Для учета конвекции создадим и назначим жесткость для стержней на обогреваемых сторонах, согласно рис. 11. Выделяем стержни, открываем контекстную вкладку Стержни и далее Жесткости. Добавляем тип жесткости Конвекция (двухузловые) и задаем параметры согласно рис. 11. Подтверждаем создание жесткости и применяем её выделенным стержням.

Рис. 11

Переключим загружение на номер 6. Снова выделяем стержни, для задания им температуры конвекции. См. рис. 12.

Рис. 12

По результатам выполнения операций расчетная схема примет следующий вид – см. рисунок 13.

Рис. 13

Учет лучистого теплообмена будет осуществляться путем задания теплового потока на ребро пластины. Для задания теплового потока необходимо выделить узлы обогреваемых граней и примыкающие к ним пластины. Выполнить это можно путем выделения сначала стержней на обогреваемых гранях, см. рисунок 14. Выделить стержни можно рамкой на экране (с активированными инструментами выбора вертикальных и горизонтальных стержней, пункт 1 на рисунке 14), либо с помощью Полифильтра. После выделения стержней необходимо отметить также узлы, принадлежащие им — выполняется путем нажатия кнопки Отметить узлы, принадлежащие отмеченным элементам (см. пункт 3 на рисунке 14). Загружение сменим на номер 7.

Рис. 14

Чтобы отметить пластины, принадлежащие выбранным узлам, необходимо нажать на кнопку Отметить элементы, принадлежащие к отмеченным узлам на панели инструментов, см. рисунок 15.

Рис. 15

Таким образом у нас отмечены на схеме пластины, узлы и стержни на обогреваемых гранях. Выберем контекстную вкладку Пластины и выберем далее Нагрузка на пластины. В качестве параметров нагрузки на ребро пластины укажем величину теплового потока равную единице. Активируем галочку напротив номером узлов пластин, поскольку мы на схеме их явно указали. См. рисунок 16.

Рис. 16

Поскольку в отмеченных элементах присутствовали стержни, программа выдаст предупреждение, что задаваемая нагрузка на ребра пластины не применима к стержням. Закроем предупреждение. См. рисунок 17.

Рис. 17

Сформируем динамическое загружение, характеризующее интенсивность нагрева конструкции. Для этого выберем на панели Расчет — Динамика во времени от статических загружений и в появившемся окне зададим следующие параметры. Номер загружения укажем — 6. В качестве закона преобразования укажем — 1. Ломан. с произв. шагом. Количество точек укажем 22. И сформируем таблицу путем ввода попарно значений времени в секундах и температуры огневого воздействия. Значение параметров приведено на рисунке 18.

Рис. 18

График по введенным значениям в таблицу можно посмотреть путем установки галочки у значка лупы. Появившийся график можно задокументировать в Книгу отчетов. По завершении ввода подтвердим создание динамического загружения (см. рисунок 19).

Рис. 19

Повторим операцию, но теперь укажем в качестве загружения — 7-ой номер, в качестве закона — 15 Тепловое излучение, укажем также 22 точки и повторим создание таблицы со аналогичными значениями. Коэффициент поглощения укажем 0.75, коэффициент излучения — 1, и угловой коэффициент — 1. Подтвердим создание динамического загружения. См. рисунок 20.

Рис. 20

Укажем шаг и пределы интегрирования через инструмент Динамика во времени на вкладке Расчет. Для расчета конструкции с шагом 1 минута в течении 4-х часов введем соответствующие значения (в секундах) в графы Шаг интегрирования и Время интегрирования. Количество дробления шага укажем 1. См. рисунок 21.

Рис. 21

Для точного определения значения температуры в искомой точке, добавим её путем ввода узла по координатам. Добавим точку соответствующая положению нижнего стержня в гофре. См. рисунок 22.

Рис. 22

Ту же операцию проделаем для указания положения верхнего стержня. Поскольку сечение конструкции регулярное, добавлять указанные точки в каждое ребро нет необходимости. См. рисунок 23.

Рис. 23

Задача подготовлена к расчету. Выполним расчет. См. рисунок 24.

Рис. 24

После завершения расчетов укажем на какой момент времени необходимо сформировать результаты. Для этого на панели Инструменты выберем инструмент Шаги интегрирования динамики во времени (символ с часами) и отметим в появившемся окне галочками интересуемые моменты времени.

Для просмотра изополей температур нагрева сечения конструкции выберем на панели Температура инструмент Изополя температур. На нижней панели выберем интересуемое время, например 60 [минут]. См. рисунок 25.

Рис. 25

Аналогично просмотрим изополя температур на 100-ую минуту. См. рисунок 26.

Рис. 26

Для определения температур на момент 60-ой минуты нагрева сечения в интересуемых точках, отфрагментируем участок с добавленными узлами. Во флагах рисования отметим показывать значения мозаики контрастным цветом. Искомые значения температуры составляют 38.7 С для верхней арматуры и 630 С для нижней арматуры. См. рисунок 27.

Рис. 27

Автор: Никитин Ион

ООО «Фарм Дизайн»

РЕШЕНИЕ НЕЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ | Опубликовать статью ВАК, elibrary (НЭБ)

Брыков Н.А.

Ассистент кафедры плазмогазодинамика и теплотехника, Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова, Санкт-Петербург

РЕШЕНИЕ НЕЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ

Аннотация

В статье рассмотрено численное решение нелинейной нестационарной задачи теплопроводности для определения температурного поля в многослойной пластине с внутренними источниками тепла. В модели учитывается зависимость коэффициента теплопроводности от температуры, и моделируется излучение на границах пластины. Изложена неявная двухслойная схема для метода прогонки. Дискретизация нестационарного уравнения теплопроводности производится с помощью локально одномерной, абсолютно устойчивой схемы. Представлены результаты расчета.

Ключевые слова: нестационарная теплопроводность, излучение на границе, метод прогонки.

Brykov N.A.

Assistant of the Department of heat engineering and plasmagasdynamic, Baltic State Technical University«VOENMEH» named after D.F. Ustinov, St. Petersburg

SOLUTION OF NONLINEAR TRANSIENT HEAT CONDUCTION PROBLEM

Abstract

The article deals with the numerical solution of nonlinear transient heat conduction problem for the determination of the temperature field in a multilayer plate with internal heat sources. The model takes into account the dependence of thermal conduction coefficient on the temperature, and is modeled on the radiation plate boundaries. Presented is an implicit two-layer scheme for the sweep method. Discretization of transient heat equation is performed by locally-dimensional, absolutely stable scheme.

Keywords: transient heat conduction, radiation on the borders, sweep method.

Литература

1. Чиркин В.С. Теплофизические свойства материалов ядерной техники. М.: Атомиздат, 1968 г. – 484 с.
2. Самарский А.А., Гулин А.В. Численные методы: Учеб. пособие для вузов. – М.: Наука, 1989. – 432 с.

References

1. Chirkin V.S. Teplofizicheskie svojstva materialov jadernoj tehniki. M.: Atomizdat, 1968 g. – 484 s.
2. Samarskij A.A., Gulin A.V. Chislennye metody: Ucheb. posobie dlja vuzov. – M.: Nauka, 1989. – 432 s.

Разностные схемы для уравнения теплопроводности

Составление системы конечно-разностных уравнений. Используя неявную конечно-разностную схему для уравнения теплопроводности  [c.195]

Решение получить численным методом е помощью ЭВМ на разностной сетке с числом узлов, равным 7, используя явную или неявную конечно-разностную схему для уравнения теплопроводности. Шаг по времени принять равным 0,15 с. Для того чтобы при указанных условиях получить наименьшую погрешность аппроксимации, положить комплекс аДт/(Ддс) равным 1/6. Результаты расчета сравнить с точным решением.  [c.202]

Разностные схемы для уравнения теплопроводности  [c.143]

Устойчивость разностных схем для уравнения теплопроводности  [c.186]

Для явной разностной схемы решення уравнения теплопроводности, рассмотренной в этой главе, это утверждение справедливо при к=0 11 ).— Прим, ред.  [c.129]

Конечно-разностная аппроксимация уравнений распространения тепла. Приступим к построению разностной схемы для уравнения энергии и соотношений для потоков теплопроводности и излучения. Для этого предварительно преобразуем тождественно закон сохранения энергии (VI. 1). Используем значения и / из уравнений состояния (VI. 13) и производную от потока поглощаемой энергии из закона Бугера— Ламберта (VI.2). В результате получим  [c.172]

Консервативная схема для уравнения теплопроводности. Выше были рассмотрены некоторые способы построения разностных схем, аппроксимирующих систему одномерных нестационарных уравнений газодинамики без учета реальных диссипативных процессов. Обратимся теперь к случаю, когда в задаче присутствуют процессы теплопроводности. Изменится лишь уравнение энергии, которое для одномерного плоского случая имеет вид  [c.143]

Выбор конечно-разностной схемы для численного решения уравнения теплопроводности. Уравнение теплопроводности при переменных граничных условиях и наличии лучистого теплообмена на границе тела может быть решена методом сеток. При решении задачи по явной разностной схеме допустимый шаг по времени  [c.194]

В данном разделе сначала коротко рассмотрим основные понятия теории численных методов, а затем более подробно остановимся на применении конечно-разностных схем для решения уравнений теплопроводности. Метод конечных элементов будет изложен в следующей главе.  [c.69]

Рассмотрим пример такой неудачной разностной схемы для одномерного стационарного уравнения с переменной теплопроводностью X (х)  [c.84]

Все рассмотренные нами ранее разностные схемы для решения уравнений теплопроводности являются реализациями метода конечных разностей. Системы алгебраических уравнений для определения численного решения мы получали путем замены производных в дифференциальном уравнении и в граничных условиях или в уравнениях теплового баланса для элементарных ячеек конечными разностями. Таки.м образом, в методе конечных разностей отправной точкой для получения приближенного решения является дифференциальная краевая задача. Однако искомое поле можно находить и из решения соответствующей вариационной задачи. На ее численном решении основан получивший широкое распространение метод конечных элементов (МКЭ) [7, 27].  [c.128]

Мы рассмотрели конечно-разностные схемы для решения стационарного уравнения энергии. В случае нестационарной задачи построение соответствующ,их схем производится на основе приведенных аппроксимаций конвективного и кондуктивного потоков точно так же, как это делалось для нестационарного уравнения теплопроводности, т. е. можно использовать явную или неявную схемы. В явной схеме потоки берут с предыдуш,его шага, в неявной — с текущего. Можно ввести и схему с весами. Отмеченные выше отрицательные и положительные свойства аппроксимаций (5.6)—(5.8) проявляются и при решении нестационарных задач. В частности, даже неявная схема с разностью вперед является неустойчивой при любом соотношении шагов по пространственной и временной переменным. С другой стороны, неявная схема с аппроксимацией разностью против потока безусловно устойчива.  [c.162]

Конечно-разностные схемы для решения двухмерных и трехмерных задач. Рассмотренный выше метод решения систем неявных конечно-разностных уравнений применим и при решении двухмерных задач нестационарной теплопроводности в случае использования следующей разностной схемы переменных направлений  [c.92]

Записывая (3.24) для всех внутренних точек верхнего слоя, получаем систему алгебраических уравнений, решение которой рассмотрено в 3.4. Аналогичные разностные схемы можно построить и для двумерного уравнения теплопроводности. Некоторые из схем исследованы в гл. 5.  [c.81]

Решение задач теплопроводности может быть получено еще одним численным методом — метод ом конечных элементов. Математической основой метода конечных элементов является вариационное исчисление. В отличие от метода конечных разностей, в котором исходные дифференциальные уравнения непосредственно используются для построения разностной схемы, в методе конечных элементов дифференциальное уравнение теплопроводности и соответствующие граничные условия используются для постановки вариационной задачи, которая затем решается численно.  [c.246]

Разностная схема и разностное решение. Основные понятия теории разностных схем разберем на примере одномерного нестационарного уравнения теплопроводности для пластины с внутренним источником теплоты  [c.70]

Проиллюстрируем описанную методику построения разностной схемы на примере стационарного уравнения теплопроводности для стержня с боковым теплообменом  [c.88]

Совокупность разностного уравнения, граничных и начальных условий называется разностной схемой. Рассмотрим разностную схему решения одномерного уравнения теплопроводности для некоторой скалярной величины Т, под которой можно понимать температуру пли мгновенное значение напряженности электрического либо магнитного поля в металле  [c.128]

В заключение следует отметить, что нелинейное уравнение теплопроводности при произвольной зависимости X=f T) сравнительно легко представляется в ко-нечно-разностной форме различных видов. Расчетные зависимости с симметричным смещением обеспечивают высокую точность [формула (2-121)]. Однако в случае ярко выраженной несимметричности температурного поля, что имеет место в элементах конструкций тепловых машин, несимметричное смещение может обеспечить требуемую точность при большей простоте расчетных зависимостей [формулы (2-119), (2-120)]. Учет нелинейности усложняет расчетные зависимости для определения температуры. Кроме того, учет нелинейности приводит к тому, что коэффициенты в расчетных зависимостях являются переменными. Схема расчета, расчетный бланк и порядок проведения расчета сохраняются такими же, как и при решении линейного уравнения теплопроводности. Линеаризация уравнения теплопроводности при пользовании численным методом существенных преимуществ не дает.  [c.99]

Упражнение 6.1. Показать, что для п-мерного уравнения теплопроводности в случае равномерной сетки hi = / 2 = = = h) условие устойчивости разностной схемы имеет вид  [c. 200]

Таким образом, для многомерного уравнения теплопроводности условие устойчивости разностной схемы становится более жестким.  [c.200]

НОЙ катастрофе. Классическим историческим примером здесь является явная схема Ричардсона для параболического уравнения теплопроводности, в которой использовались конечно-разностные аппроксимации производных центральными разностями как по пространственным переменным, так и по времени. О Брайен с соавторами [1950] показал, что эта схема безусловно неустойчива ).  [c.18]

Видно, что структура системы уравнений (6.25) представляет рекуррентное матричное соотношение типа (6.20). Следует отметить, что решение задачи нестационарной теплопроводности с использованием схемы (6.25) дает лучшие результаты для первых временных шагов, чем решение с использованием центральной разностной схемы (6.17). Сказанное иллюстрируется на примере решения задачи о разогреве призматического стержня (рис. 6.1).  [c.110]

Чтобы максимально облегчить понимание проблем, которые возникают при конструировании разностных схем для уравнений механики сплошной среды, ограничимся рассмотрением законов сохранения массы, количества дви зкения и энергии в одномерном случае в виде (1.131) — (1.133). Система трех уравнений (1.131) — (1.133) содержит семь искомых функций (Р, V, Е, 17, 8, 82, д) от двух независимых аргументов (t — время, г — эйлерова координата). Динамические процессы в твердых телах протекают за времена настолько малые, что теплопроводность не успевает повлиять на термодинамические характеристики вещества. Поэтому в урав-  [c.217]

Для построения консервативной схемы можно использовать интегроинтерполяционный метод [25] (или метод элементарных балансов), существо которого состоит в том, что разностная схема строится на основе интегральных законов сохранения. В результате получается разностный аналог закона сохранения для ячейки сетки. В качестве примера рассмотрим построение консервативной схемы для стационарного уравнения теплопроводности (или диффузии)  [c. 251]

Разностные уравнения (5.27) — (5.31) связывают значения сеточной функции в двух соседних сечениях по оси z с номерами (т —1) и т. При известных значениях Un,m-i ( . Л г) эти уравнения образуют систему N уравнений относительно значений сеточной функции в сечении z z — Система уравнений имеет трехдиагональную матрицу и может быть решена методом прогонки, которая проводится поперек трубы . Таким образом, построенная разностная схема аналогична неявной схеме для нестационарного одномерного уравнения теплопроводности, с тем отли-чием, что роль временных слоев играют поперечные сечения 2 . В первом сечении (т = 1) температуры задаются граничным условием (5.32), а далее последовательно для каждого сечения решается методом прогонки система разностных уравнений (5.27)—(5.31) относительно неизвестных (п = 1,. .., Nr) и определяются тем-  [c.165]

Для решения системы нелинейных уравнений параболического типа (1.8). .. (1.11) с краевыми условиями (1.12). … .. (1.14) может быть применен метод сеток с использованием явной схемы, согласно которому система уравнений приводится к безразмерному виду и записывается в конечных разностях. Вид конечно-разностных аналогов исходных уравнений и метод их решения применительно к рассматриваемой задаче представлены в [9]. Алгоритм решения этой задачи бьш реализован в виде программы расчета на БЭСМ-4М. При расчете задаются геометрические размеры пучка, параметры потока теплоносителя на входе в пучок, распределение тепловыделения (теплоподвода) у по длине и радиусу пучка и физические свойства теплоносителя. Для замыкания системы уравнений из эксперимента определяются эффективные коэффициенты турбулентной теплопроводности Хдфф, вязкости эфф п коэффициент гидравлического сопротивления % в виде зависимотей от критериев подобия, характеризующих процесс [39].  [c.16]

В последующих трех параграфах излагается гибридная разностная схема, являющаяся обобщением этих двух алгоритмов и предназначенная для расчета связанной задачи нагружения многослойного препятствия импульсом излучения с учетом плавления и испарения наружного слоя [60]. Причем в предлагаемом виде конечно-разностная методика позволяет учитывать и вязко-пластическое поведение материала, а распространение алгоритма А. А. Самарского с параболического уравнения теплопроводности на гиперболическое дает возможность численно изучать инерционность распространения тепла. Объединение обоих алгоритмов в связанной задаче и включение в общую схему расчета роста микроповрежденности достигается с помощью итерационной процедуры.  [c.167]

Метод раздельных прогонок для разностных схем магнитной гидродинамики. По сравнепию с газовой динамикой система уравнений магнитной гидродинамики с теплопроводностью является более сложной,— здесь появляются дополнительные уравнения,  [c.330]

В практических задачах времт тоже должно быть дискретизировано, что предполагает применение метода конечных разностей. Например, схема- Кранка — Николсона симметрична относительно п+1/2 при вычислении uf tn+ ) через и потому имеет точность порядка At . Таким образом, окончательно вычисленное приближение содержит эту ошибку, как и ошибку метода Галёркина, вызванную дискретизацией по х. Последнюю из них мы проанализируем подробно и покажем, что при к 2т ее оптимальный порядок для 5-й производной тоже р -вен Этот результат применяется к уравнениям параболического типа, например к уравнению теплопроводности Ь — эллиптический оператор того же типа, что и в стационарных задачах. В случае гиперболических уравнений, не содержащих диссипативных членов, возможности метода конечных элементов несколько меньше трудности в сравнении с явными разностными методами- могут оказаться слишком большими. Тем не менее даже в этом случае достигнуты значительные результаты исследование границ можно проводить почти автоматически в гл. 7 включен набросок теории метода конечных элементов для гиперболического случая.  [c.139]

Схему (2.13а) можно интерпретировать как алгоритм расшепления по физическим признакам в первом уравнении (2. 136) учитывается только конвекция, во втором — только диффузия. Соответственно обращаемый оператор в первом уравнении после умножения его на А совпадает с оператором, обращаемым при решении разностных уравнений для уравнения переноса (1.8). Второе уравнение (2.136) аналогично разностному уравнению теплопроводности, причем имеется возможность выбора обращаемого оператора Е — атбг. Определяя скалярными про-  [c.53]

Для расчета двумерных течений особенно эффективной схемой с введением явной искусственной вязкости является схема Русанова [1961]. В основе схемы Русанова лежит введение членов с искусственной диффузией общего вида д авд11 /дх) /дх в конечно-разностные недиссипативные уравнения для ди/д1 (где и р, ри, pv, Ее), причем берутся разности вперед по времени и центральные разности по пространственным переменным. Таким образом, в схему вводится не только искусственная вязкость, но и искусственная теплопроводность и искусственная диффузия массы ). Коэффициент искусственной диффузии пропорционален У +а и некоторому эмпирически подбираемому параметру со. Форма д (ссвди/дх)/дх позволяет получить более точные решения со скачками, чем более простая форма авдЮ/дх (Ван Леер [1969]).  [c.350]

Сканирующая микроскопия теплопроводности (SThM)

Сканирующая микроскопия теплопроводности (SThM) высокого разрешения АСМ серии XE 

Сегодня существует растущий интерес к рассеиванию тепла в наноразмерных материалах. Режим сканирования теплопроводности серии XE (SThM) был разработан для анализа температурных свойств на наноразмерном уровне. В серии XE SThM используются нанометрические температурные датчики для обеспечения беспрецедентно высокого температурного разрешения и объемного изображения, высокой чувствительности с уникальной схемой обнаружения сигнала. Методика SThM серии XE отображает температурные свойства поверхности образца с помощью нанометрического температурного датчика с резистивным элементом. Серия XE SThM работает в двух режимах: температурная контрастная микроскопия (TCM) и контрастная микроскопия  проводимости (CCM). TCM позволяет пользователю измерять колебания температуры поверхности образца. CCM позволяет пользователю измерить температурную проводимость поверхности образца.

Рисунок 1. Схема системы серии SThM

На рисунке 1 представлена схема системы SThM серии XE.  Резистивный элемент, выполненный в форме «V», установлен на конце кантилевера. Если расстояние между зондом и поверхностью образца контролируется схемой АСМ, одно плечо температурного зонда выполнено в форме моста Уитстона (рисунок 1). Это мост обеспечивает обратную связь, регулирует и балансирует напряжение моста, чтобы измерить температуру зонда (TCM) или поддерживать постоянную температуру зонда (CCM). Топографическое изображение АСМ можно получить на основе изменений отклонения амплитуды кантилевера. Поэтому топографическую информацию может отделить от вариации температурных свойств образца, оба изображения получаются одновременно.

Температурный нанозонд серии XE

Ключевым элементом SThM является зонд SThM, который представляет собой резистивный термометр (или нагревательный элемент в режиме CCM) и является одновременно зондом АСМ. Сопротивление зонда SThM изменяется в соответствии с температурой контактной поверхности, оно контролируется мостом Уитстона. Прежняя конструкция SThM, которая была выполнена травлением провода, не способна обеспечить достаточно высокое трехмерное, температурное разрешение,  ограничено геометрией температурного проводного зонда, то есть провода Wollastone. Серия XE SThM использует нанометрический температурный зонд, в котором резистивный элемент литографически нанесен на зонд АСМ.

Рисунок 2. Изображения SEM серии (a) XE нанометрического температурного зонда и (b) провода Wollastone.

На рисунке 2 (a) и 2 (b) представлены изображения в сканирующей электронной микроскопии (SEM) проводного температурного датчика Wollastone и нанометрического температурного датчика, который используется в серии XE SThM. Радиус зонда нанометрического датчика составляет примерно 100 нм, обеспечивая высокое температурное разрешение. Проводной датчик Wollastone имеет размеры, которые больше на несколько сотен нм.

Рисунок 3. Сравнение топографического изображения клемм HSQ диаметром 1мкм на силиконовой подложке (размер скана 5 мкм) с помощью нанометрического температурного датчика (a) серии XE и провода (b) Wollastone.

Рисунок 4. Сравнение изображения температурной проводимости клемм HSQ диаметром 1 мкм на силиконовой подложке (размер скана 5 мкм) с помощью нанометрического температурного датчика (a) серии XE и провода (b) Wollastone.

На рисунках 3 и 4 выполнено сравнение изображений, полученных нанометрическим температурным датчиком серии XE и проводным датчиком Wollastone. Образец – клеммы из водородного силсесквиоксана (HSQ) диаметром 1мкм на силиконовой подложке. Разное разрешение на топографическом и температурном изображениях явно прослеживается для нанометрического температурного датчика XE, который обладает, очевидно, превосходным температурным разрешением. Следует обратить внимание, что подобные улучшения в разрешении и чувствительности достигнуты путем сочетания преимуществ  нанометрического температурного датчика и чувствительности самого режима SThM в серии XE.

Температурный контрастный режим (TCM)

В режиме TCM резистивный элемент нанометрического температурного датчика серии XE используется как резистивный термометр. Температура зонда меняется по мере сканирования поверхности образца. Изменение температуры провода приводит к изменению его сопротивления. Температуру очень малой зоны можно измерить с помощью постоянного тока, который называется «током датчика», протекающего через зонд по измерению сопротивления, как показано на рисунке 5. Сначала зонд входит в температурное равновесие с поверхностью образца, таким образом, его сопротивление является постоянным. В этот момент переменное сопротивление в мосту регулируется таким образом, что разница потенциалов между точками 1 и 2 становится равной нулю. Затем, температура зонда меняется по мере того, как он сканирует поверхность образца. Соответствующее изменение сопротивления зонда нарушает баланс напряжений моста, что приводит к изменению разницы потенциалов между точками 1 и 2. Это так называемая «ошибка SThM». Данная ошибка SThM используется для формирования изображения SThM в режиме TCM.

Ток, проходящий через зонд в режиме TCM, имеет достаточно малое значение, поэтому самонагрева зонда не происходит (изменение сопротивления из-за нагрева вызывает ошибку измерения температуры). Также в режиме TCM скорость сканирования ограничена временем, которое требуется для достижения зондом температурного равновесия с поверхностью образца.

Режим контрастной проводимости (CCM)

В режиме контрастной проводимости (CCM) резистивный элемент нанометрического температурного датчика серии XE используется в качестве резистивного нагревателя. Подводится определенное количество энергии к зонду, чтобы сохранить его температуру постоянной с использованием контура обратной связи. Энергия, необходимая для поддержания заданной температуры, характеризует локальную теплопроводность.  Схема CCM представлена на рисунке 6.

Если предварительно заданная температура нагревательного зонда значительно выше температуры образца в точке контакта, тепло передается от зонда в образец, в результате этого происходит охлаждение зонда. Контур обратной связь «чувствует» это изменение, балансирует напряжение моста, восстанавливает сопротивление зонда (или его температуру) на заданное значение. Набор данных SThM серии XE характеризует напряжение обратной связи, Vout, применяемое в мосту. Но теплопроводность образца пропорциональна тепловому потоку (~Vout2_), когда зонд входит в контакт с образцом. Можно воспользоваться методом простой калибровки для измерения абсолютной теплопроводности.

Тепловой поток между зондом и образцом при исследовании контролируется с учетом факторов:

• теплопроводность образца;
• контактная зона зонда;
• температурная разница между зондом и образцом.

Для большинства образцов изменения контактной зоны «зонд-образец» незначительны. Благодаря высокой температурной массе образец имеет постоянную температуру (разница температур между зондом и образцом также остается постоянной, так как температура датчика контролируется контуром обратной связи). Поэтому изменения теплового потока могут быть вызваны только изменением теплопроводности образца.

Поскольку теплопроводность образца изменяется в процессе сканирования, температура зонда также стремится к изменению, но мост Уинстона использует ошибку SThM и контур обратной связи для балансировки напряжения на зонде, которое поддерживает температурную константу на заданном уровне.

Нанометрическое температурное изображение серии XE

На рисунке 7 показана топография высокого разрешения и изображение теплопроводности клеммы HSQ диаметром 4,3мкм на силиконовой подложке с помощью SThM серии ХЕ с нанометрическим температурным зондом. Неоднородность в теплопроводности из-за «включений» в составе HSQ наблюдается в контрасте на плоской топографии.

На рисунке 8 топография высокого разрешения и теплопроводность малых клемм HSQ диаметром 0,2мкм на силиконовой подложке отображаются, с помощью серии XE SThM с нанометрическим температурным зондом. На изображении с теплопроводностью можно также наблюдать «включения», которые отсутствуют на топографии.

Очевидно, что серия XE SThM имеет превосходное пространственное и тепловое разрешение. Она открывает большие возможности в изучении нанометрических температурных свойств разных наноструктурных материалов.

Рисунок 7. (a) Топография высокого разрешения SThM и теплопроводность (b) клеммы HSQ диаметром 4,3 мкм на силиконовой подложке (размер скана 5 мкм) с помощью SThM серии ХЕ с нанометрическим температурным зондом.

Рисунок 8. (a) Топография высокого разрешения SThM и изображение теплопроводности (b) клемм HSQ диаметром 0,2мкм на силиконовой подложке (размер скана 5 мкм) с помощью SThM серии ХЕ с нанометрическим температурным зондом.

Микроскопы, работающие в режиме сканирующей микроскопии теплопроводности (SThM):

СПЕКТРАЛЬНАЯ СОГЛАСОВАННОСТЬ РАЗНОСТНЫХ СХЕМ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ | Волков

1. Lele, S. K. Compact finite difference schemes with spectral-like resolution / S. K. Lele // J. Comput. Phys. – 1992. – Vol. 103, №. 1. – P. 16–42.

2. Tam, C. K. W. Dispersion-relation-preserving finite difference schemes for computational acoustics / C. K. W. Tam, J. C. Webb // J. Comput. Phys. – 1993. – Vol. 107, №. 2. – P. 262–281.

3. Волков, В. М. Консервативные разностные схемы с улучшенными дисперсионными свойствами для нелинейных уравнений шредингеровского типа / В. М. Волков // Дифференц. уравнения. – 1993. – т. 29, №. 7. – С. 1156–1162.

4. Сергиенко, а. Г. Цифровая обработка сигналов / А. Г. Сергиенко. – СПб.: БХВ-Петербург, 2011. – 768 с.

5. Improved split-step method for efficient fiber simulations / M. Plura [et al.] // Electron. Lett. – 2001. – Vol. 37, № 5. – P. 286–287.

6. Волков, В. М. Метод дробных шагов с использованием рекурсивных цифровых фильтров для решения нелинейных уравнений Шредингера / В. М. Волков, А. С. Циунчик // Докл. Нац. акад. наук Беларуси. – 2009. – Т. 53, № 5. – С. 22–25.

7. Волков, В. М. Оптимизация компактных разностных схем спектрального разрешения для нестационарного уравнения Шредингера на основе методов цифровой обработки сигналов / В. М. Волков, А. Н. Гуревский, И. В. Жукова / Вестн. БГУ. Сер. 1, Физика. Математика. Информатика. – 2015. – № 3. – С. 84–89.

8. Самарский, а. а. теория разностных схем / А. А. Самарский. – М.: Наука, 1989. – 616 с.

9. Саульев, В. К. О методах повышения точности и двухсторонних приближениях к решению параболических уравнений / В. К. Саульев // Докл. АН СССР. – 1958. – т. 118. – С. 1088.

Явная разностная схема для уравнения теплопроводности

Используя шаблон
для каждого внутреннего узла области
решения апроксимируется уравнение
теплопроводности

Отсюда найдем:

Используя начальные
и граничные условия, находят значения

сеточной функции во всех узлах на нулевом
временном уровне.

Затем с помощью
соотношений

находятся значения
этих функций во всех внутренних узлах
на первом временном уровне, после чего
находим значение на граничных узлах

В результате мы
находим значение функций во всех узлах
на первом временном уровне. После этого
с помощью этих соотношений находим все
остальные значения и т.д.

В рассматриваемой
разностной схеме значения искомой
функции на следующем временном уровне
находится непосредственно, явно с
помощью формулы

Поэтому рассматриваемая
разностная схема, использующая этот
шаблон, называется явной
разностной схемой.
Точность её имеет порядок

.

Данная разностная
схема проста в использовании, однако
она обладает существенным недостатком.
Оказывается, что явная разностная схема
обладает
устойчивым решением
только в том случае, если
выполняется условие:

Явная разностная
схема является
условно устойчивой.
Если условие не выполняется, то небольшие
погрешности вычислений, например,
связанные с округлением данных компьютера
приводит к резкому изменению решения.
Решение становится неприемлемым для
использования. Это условие накладывает
весьма жесткие ограничения на шаг по
времени, что может оказаться неприемлемым
из-за значительного увеличения времени
счета решения этой задачи.

Рассмотрим
разностную схему, использующую другой
шаблон

Метод
36

Неявная разностная схема для уравнения теплопроводности

Подставим в
уравнение теплопроводности:

Это соотношение
записывается для каждого внутреннего
узла на

временном уровне и дополняется двумя
соотношениями, определяющими значения
в граничных узлах. В результате получается
система уравнений для определения
неизвестных значений функции на

временном уровне.

Схема решения
задачи следующая:

С помощью начальных
и граничных условий находится значение
функции на нулевом временном уровне.
Затем с помощью этих соотношений и
граничных условий строится система
линейных алгебраических уравнений для
нахождения значения функции на первом
временном уровне, после чего опять с
помощью этих соотношений строится
система, и находятся значения на втором
временном уровне и т.д.

Отличие
от явной схемы
— значения на очередном временном уровне
вычисляются не непосредственно с помощью
готовой формулы, а находится путем
решения системы уравнений, т.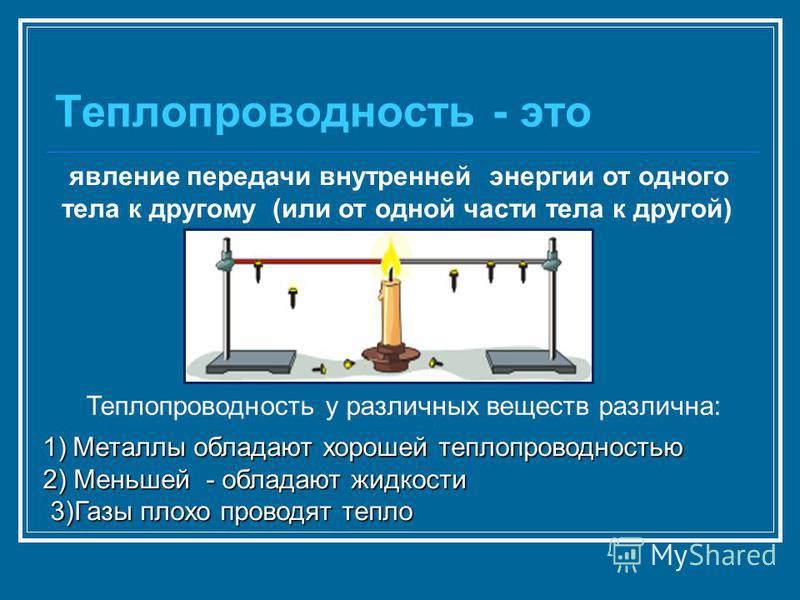 е. значения
неизвестных находятся неявно путем
решения СЛАУ. Поэтому разностная схема
называется неявной. В отличие от явной
неявная является абсолютно устойчивой.

Тема
№9

Задачи оптимизации.

Эти задачи являются
одними из важнейших задач прикладной
математики. Под
оптимизацией понимают
выбор наилучшего варианта из всех
возможных решений данной задачи. Для
этого необходимо сформулировать решаемую
задачу как математическую, придав
количественный смысл понятиям лучше
или хуже. Обычно в процессе решения
необходимо найти оптимизируемые значения
параметров. Эти параметры называют
проектными.
А число проектных параметров определяет
размерность
задачи.

Количественная
оценка решения производится с помощью
некоторой функции зависящей от проектных
параметров. Эта функция называется
целевой.
Она строится таким образом, чтобы
наиболее оптимальное значение
соответствовало максимуму(минимуму).

—
целевая функция.

Наиболее просты
случаи, когда целевая функция зависит
от одного параметра и задаётся явной
формулой. Целевых функций может быть
несколько.

Например, при
проектировании самолёта требуется
одновременно обеспечить максимальную
надежность, минимальные вес и стоимость
и т.д. В таких случаях вводится система
приоритетов.
Каждой целевой функции ставится в
соответствие некоторый целевой множитель
в результате получается обобщенная
целевая функция(функция компромиссов).

Обычно оптимальное
решение ограничено рядом условий
связанных с физической функцией задачи.
Эти условия могут иметь вид равенств
или неравенств

Теория и методы
решения задач оптимизации при наличии
ограничений составляют предмет
исследований одного из разделов
прикладной математики – математического
программирования.

Если целевая
функция линейна относительно проектных
параметров и ограничения, накладываемые
на параметры также линейны, то возникает
задача
линейного программирования.
Рассмотрим методы решения одномерной
задачи оптимизации.

Требуется найти
значения

на
при
которых целевая функция имеет максимальное
значение. Если целевая функция задана
аналитически и может быть найдено
выражение для её производных, то
оптимальное решение будет достигаться
либо на концах отрезка, либо в точках в
которых производная обращается в ноль.
Это критические точки

и
.
Необходимо найти значения целевой
функции во всех критических точках и
выбрать максимальное.

В общем случае для
нахождения решения применяют различные
методы поиска. В результате происходит
сужение отрезка содержащего оптимальное
решение.

Рассмотрим некоторые
из методов поиска. Предположим, что
целевая функция на промежутке

имеет один максимум. В этом случае,
разбив

узловыми точками
,
число которых
,
вычисляют целевую функцию в этих узловых
точках. Предположим, что максимальное
значение целевой функции будет в узле
,
тогда можно считать, что оптимальное
решение находится на интервале
.
В результате произведено сужение
отрезка, содержащего оптимальное
решение. Полученный новый отрезок вновь
разбивают на
частей
и т.д. При каждом разбиении отрезок,
содержащий оптимальное решение
уменьшаются в
раз.

Предположим, что
произведено
шагов
сужения. Тогда исходный отрезок

уменьшается в
раз.

То есть, делаем
пока выполняется
(*)

При этом производится

вычислений
целевой функции.

Требуется найти
такое значение,

чтобы выражение (*) было получено при
наименьшем

числе вычислений
.

Метод
37

Теплопроводность диэлектрических материалов для печатных плат — C-Therm Technologies Ltd.

Печатная плата (PCB) определяется как элемент, который «механически поддерживает и электрически соединяет электронные компоненты с помощью токопроводящих дорожек, контактных площадок и других элементов, вытравленных из медных листов, ламинированных на непроводящую подложку». (определение любезно предоставлено Википедией). Печатные платы могут быть односторонними или двусторонними, а также иметь несколько слоев. В некоторые из них встроены компоненты, позволяющие создавать сложные и продвинутые схемы (рис. 1).

Рис. 1. Усовершенствованная печатная плата с видимыми встроенными компонентами (Источник).

Рис. 2. Печатная плата с видимым отказом, вызванным перегревом. Такой сбой может быть из-за плохого управления температурным режимом (Источник).

Важность теплопроводности для печатных плат

Управление нагревом имеет решающее значение для производительности, надежности и долговечности печатной платы. Неадекватное управление теплом может привести к расслоению, повреждению или отказу устройства (рис. 2). Теплопроводность играет жизненно важную роль в управлении теплом и, следовательно, является ключевым параметром при проектировании печатных плат.Платформа теплопроводности C-Therm Trident — полезный инструмент для получения быстрых, точных и точных измерений теплопроводности компонентов печатной платы.

Здесь мы подробно рассказываем, как датчик C-Therm Technologies TCi может использоваться для помощи в проектировании управления нагревом печатной платы. Это примечание по применению содержит специальное предисловие Дуга Брукса, эксперта по дизайну печатных плат, регулярного автора отраслевых публикаций, таких как PCB Design 007, и владельца UltraCAD Design, Inc:

Последние 25 лет я владел сервисным бюро по проектированию печатных плат.«Горячей» темой в дизайне печатных плат является целостность высокоскоростного сигнала. Но с другой стороны, разработчиков печатных плат может интересовать, насколько горячим (буквально) становится отдельная дорожка печатной платы. Температура следа напрямую связана с надежностью. В крайнем случае, слишком горячий след может расплавить припой или вызвать расслоение платы. Но обычно мы хотим, чтобы следовые температуры были намного ниже этого. Для приложений с очень высокой надежностью (например, пилотируемый космос, медицина и т. Д.) Мы можем разрабатывать очень консервативные решения.В отношении потребительских товаров мы можем быть немного более агрессивными. Для приложений в жаркой пустыне (подумайте о военном времени) мы можем захотеть узнать, сколько тепла нам нужно рассеять с помощью каких-либо внешних средств. Кривая достигает стабильной температуры, когда нагревание трассы равняется охлаждению трассы. Нагрев дорожки вызван падением мощности I ² R на дорожке. Охлаждение следа в первую очередь является результатом проводимости через диэлектрик (материал платы) и, во вторую очередь, за счет конвекции и излучения.Лишь в последние 10 лет промышленность осознала важность диэлектрика в процессе охлаждения следа. Важным свойством материала при электронагреве является удельное сопротивление следового материала (обычно медной фольги или покрытия). Хотя фактическое удельное сопротивление следа является предметом обсуждения в промышленности, по большинству оценок оно находится между значениями чистого медь (1,7 мкОм-см) и около 2,1 мкОм-см. Важным свойством материала при охлаждении следа является теплопроводность (Вт / мK) в плоскости x, y и оси z.Это может значительно различаться в зависимости от предлагаемого материала и даже у разных производителей для одной и той же спецификации материала. Более того, не все производители предоставляют спецификации теплопроводности, особенно по оси z. Анализатор теплопроводности C-Therm может быть важным инструментом при измерении теплопроводности материала картона или при проверке соответствия продукции производителя спецификациям. Для получения дополнительной информации о взаимосвязи между током следа / температурой печатной платы см.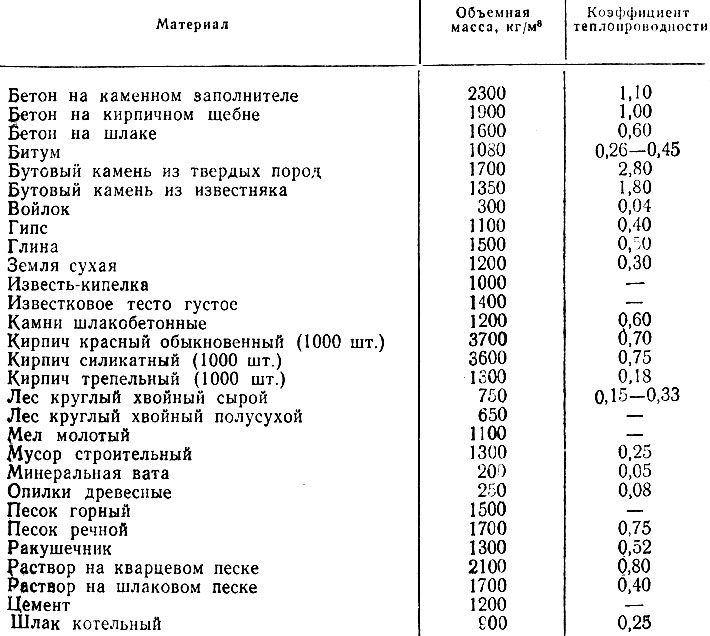 Серию из пяти статей, размещенных на сайте www.ultracad.com (еще как минимум два появятся в ближайшие месяцы)

Дуглас Брукс, президент UltraCAD Design, Inc. www.ultracad.com

Особенности корпуса

: Проверка теплопроводности диэлектрического материала печатной платы FR4

Образцы диэлектрического материала для печатных плат типа FR4 были получены в виде бледно-желтых прямоугольных призм и использовались, как предусмотрено. Теплопроводность измеряли с использованием метода модифицированного источника переходных процессов C-Therm (MTPS).

Плоская теплопроводность диэлектрического материала печатной платы типа FR4

В методе MTPS используется запатентованная технология защитного кольца, которая обеспечивает однонаправленный тепловой поток и, таким образом, измерение теплопроводности.Это позволяет легко измерять анизотропные материалы, располагая датчик вдоль различных поверхностей материала для прямого измерения анизотропии теплопроводности.

Данные по теплопроводности в сквозной плоскости были получены для трех образцов с тремя тестами по пятнадцать измерений в каждом. Было взято среднее значение трех образцов, и оно было выражено как теплопроводность через плоскость. Во всех тестах относительное стандартное отклонение составляло <1%, а для трех выборок относительная стандартная ошибка составляла 0.7%. Плоская теплопроводность объемного материала измерялась тремя тестами по пять измерений в каждом. Относительное стандартное отклонение составило 0,6% по результатам трех испытаний на теплопроводность в плоскости.

Эта работа иллюстрирует важность получения данных теплопроводности вдоль всех соответствующих осей материала в случае материалов с анизотропной теплопроводностью — в этом случае измерение только значения через плоскость приведет к значительному занижению эффективной теплопроводности материала. диэлектрический материал печатной платы.

Основы термического сопротивления | Celsia

Сегодняшний гостевой блог об основах термического сопротивления ведет доктор Джеймс Стивенс, профессор машиностроения из Университета Колорадо.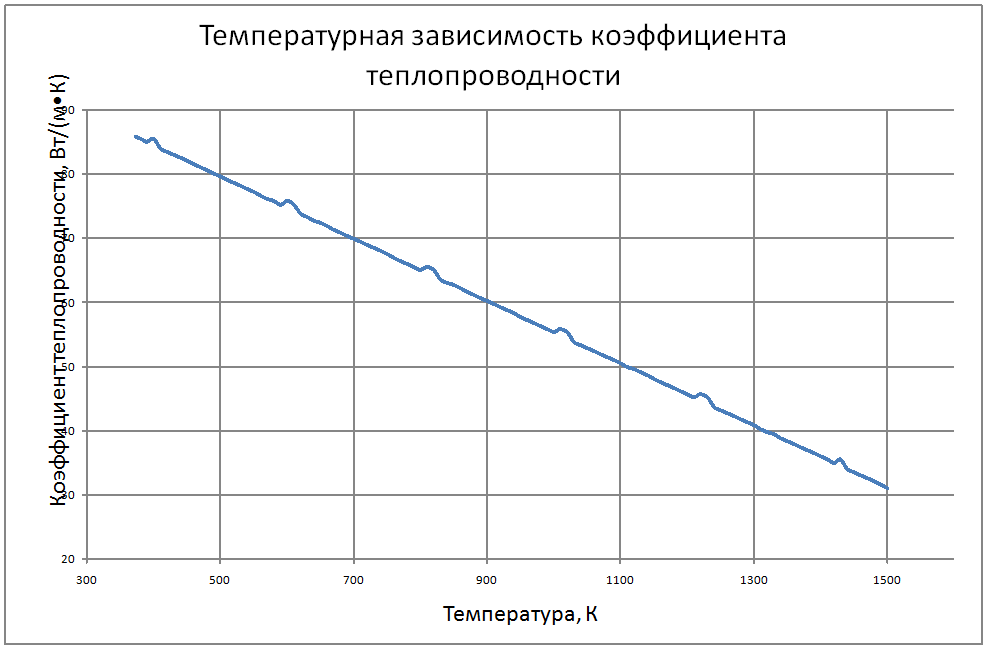 Доктор Стивенс специализируется на численном и аналитическом анализе теплопередачи, охватывающем как установившиеся, так и переходные ситуации, с приложениями к тепловой истории, тепловому отклику, электронному охлаждению, температурным профилям, тепловому расчету и определению скорости теплового потока.

Аналогия теплового сопротивления

Термическое сопротивление — это удобный способ анализа некоторых проблем теплопередачи с использованием электрической аналогии, чтобы упростить визуализацию и анализ сложных систем. Он основан на аналогии с законом Ома:

В законе Ома для электричества «V» — это напряжение, управляющее током с величиной «I». Сила тока, протекающего при заданном напряжении, пропорциональна сопротивлению (R _elec ).Для электрического проводника сопротивление зависит от свойств материала (например, медь имеет более низкое сопротивление, чем древесина) и физической конфигурации (толстые короткие провода имеют меньшее сопротивление, чем длинные тонкие провода).

Для одномерных стационарных задач теплопередачи без внутреннего тепловыделения тепловой поток пропорционален разнице температур в соответствии с этим уравнением:

где Q — тепловой поток, k — свойство материала теплопроводности, A — площадь, нормальная к потоку тепла, Δx — расстояние, на котором течет тепло, а ΔT — разность температур, движущая поток тепла.

Если мы проведем аналогию, сказав, что электрический ток течет подобно теплу, и заявив, что напряжение управляет электрическим током, как разность температур управляет тепловым потоком, мы можем записать уравнение теплового потока в форме, аналогичной закону Ома: где R _th — это тепловое сопротивление, определяемое как: Как и в случае с электрическим сопротивлением, тепловое сопротивление будет выше для небольшой площади поперечного сечения теплового потока (A) или на большом расстоянии (Δx).

Обоснование

Итак, зачем все это беспокоиться? Ответ заключается в том, что термическое сопротивление позволяет нам решать несколько сложные проблемы относительно простыми способами. Мы поговорим о различных способах его использования, но сначала рассмотрим простой случай, чтобы проиллюстрировать преимущества.

Предположим, что мы хотим рассчитать тепловой поток через стену, состоящую из трех разных материалов, и нам известны поверхностные температуры на каждой внешней поверхности, T _A и T _B , а также свойства и геометрия материала.

Мы могли бы написать уравнение проводимости для каждого материала:

Теперь у нас есть три уравнения и три неизвестных: T ₁ , T ₂ и Q.В этом случае было бы не так уж много работы, чтобы алгебраически решить эти три неизвестных, однако, если мы воспользуемся аналогией термического сопротивления, нам даже не придется проделывать столько работы:

, где

и мы может решить для Q за один шаг.

Объединение тепловых сопротивлений

Этот простой пример показывает, как последовательно объединить несколько тепловых сопротивлений, что имеет ту же структуру, что и в электрическом аналоге:

Так же, как электрические сопротивления, тепловые сопротивления также могут быть объединены параллельно или в как последовательно, так и параллельно:

Beyond Conduction

До сих пор мы говорили о тепловом сопротивлении, связанном с проводимостью через плоскую стенку.Для стационарных одномерных задач другие уравнения теплопередачи могут быть сформулированы в формате термического сопротивления. Например, рассмотрим закон охлаждения Ньютона для конвективной теплопередачи:

где Q — тепловой поток, h — коэффициент конвективной теплопередачи, A — площадь, на которой происходит теплопередача, T _s — температура поверхности. на котором имеет место конвекция, а T _inf — температура в набегающем потоке жидкости.Как и в случае с теплопроводностью, существует разница температур, движущая потоком тепла. В этом случае тепловое сопротивление будет:

Аналогично, для теплопередачи от серого тела:

где Q — тепловой поток, ε — коэффициент излучения поверхности, σ — коэффициент Стефана-Больцмана. константа, T _s — это температура поверхности излучающей поверхности, а T _surr — температура окружающей среды. Факторизуя выражение для температуры, можно записать тепловое сопротивление:

Преимущество: простая установка задачи

Формулировки термического сопротивления могут упростить решение довольно сложной задачи.Представьте, например, что мы пытаемся рассчитать тепловой поток от потока жидкости известной температуры через композитную стену к воздушному потоку с конвекцией и излучением, происходящим на стороне воздуха. Если свойства материала, коэффициенты теплопередачи и геометрия известны, установка уравнения очевидна:

Теперь для решения этой конкретной проблемы может потребоваться итеративное решение, поскольку радиационное тепловое сопротивление содержит внутри себя температуру поверхности, но установка проста и понятна.

Преимущество: Problem Insight

Формулировка термического сопротивления имеет дополнительное преимущество, так как дает очень четкое представление о том, какие части модели контролируют теплопередачу, а какие части не важны или, возможно, даже незначительны. В качестве конкретной иллюстрации предположим, что в последнем примере тепловое сопротивление на стороне жидкости составляло 20 К / Вт, что первый слой в композитной стене был пластиком толщиной 1 мм с тепловым сопротивлением 40 К / Вт, что второй слой состоял из стали толщиной 2 мм с термическим сопротивлением 0.5 К / Вт, и что тепловое сопротивление конвекции воздуха составляло 200 К / Вт, а тепловое сопротивление излучению в окружающую среду было 2500 К / Вт, исходящему от поверхности с излучательной способностью 0,5.

Мы можем многое понять в проблеме, просто учитывая тепловое сопротивление. Например, поскольку сопротивление излучения параллельно гораздо меньшему сопротивлению конвекции, оно будет иметь небольшое влияние на общее тепловое сопротивление. Увеличение коэффициента излучения стены до единицы улучшило бы общее тепловое сопротивление только на 5%.Или полное игнорирование излучения приведет к ошибке всего в 6%. Точно так же термическое сопротивление стали является последовательным и крошечным по сравнению с другими сопротивлениями в системе, поэтому независимо от того, что сделано с металлическим слоем, это не окажет большого влияния. Например, переход со стали на чистую медь улучшит общее термическое сопротивление только на 0,2%. Наконец, очевидно, что тепловое сопротивление регулируется конвекцией со стороны воздуха. Если бы можно было удвоить коэффициент конвекции (скажем, увеличив скорость воздуха), только этот шаг уменьшил бы общее тепловое сопротивление на 36%.

Проводимость за пределами плоской стены

Тепловое сопротивление также можно использовать для других геометрий проводимости, если они могут быть проанализированы как одномерные. Тепловое сопротивление теплопроводности в цилиндрической геометрии составляет:

, где L — осевое расстояние вдоль цилиндра, а r ₁ и r ₂ показаны на рисунке.

Термическое сопротивление для сферической геометрии составляет:

с r ₁ и r ₂ , как показано на рисунке.

Заключение

Термическое сопротивление — это мощный и полезный инструмент для анализа проблем, которые можно аппроксимировать как одномерные, стационарные и не имеющие источников тепловыделения.

Пожалуйста, свяжитесь с Celsia для решения следующей задачи по тепловому расчету. Мы специализируемся на разработке и производстве теплоотводов с использованием жидкостных двухфазных устройств: тепловых трубок и паровых камер.

FR4 PCB: Руководство по теплопроводности FR4 для вашей печатной платы

FR4 Управление теплопроводностью для светодиодов

Как и светодиод, который на протяжении десятилетий служил исключительно индикаторной лампой, печатная плата также оставила свое теневое существование и быстро превратилась в многофункциональный элемент электронной системы. Следовательно, он должен выдерживать высокие токи и обеспечивать охлаждение высокочастотных, но выделяющих тепло процессоров и теплоотводящих компонентов питания, что привело нас к сегодняшней теме — теплопроводности FR4.

1. Сравнение обычного двухплатного решения с комбинацией FR4 / медь

Как светодиоды UHB (светодиоды сверхвысокой яркости) с мощностью до десяти или более ватт на корпус и светодиодные матрицы с множеством светодиодов, расположенных близко друг к другу. Поскольку они используются все чаще, вопрос отвода тепла становится все более актуальным.

Это применяется, в частности, потому, что, в отличие от ламп накаливания, светодиоды излучают лишь незначительную часть тепловых потерь; практически все идет путем теплопроводности.

Конечно, есть решения, например, керамические носители или IMS PCB (изолированные металлические подложки) с толстыми алюминиевыми сердечниками. Однако они очень дороги по сравнению с классическими печатными платами FR4, и обычно требуется вторая плата для размещения электроники драйвера.

FR4 PCB с медным проводом

Moko Technology использует другой подход с »HSMtec«.Технология, которая сертифицирована в соответствии с DINEN60068-2-14 и JEDECA101-A и проверена для авиации и автомобилестроения, является избирательной: только там, где предполагается протекание больших токов через печатную плату, толстая медь.

В настоящее время доступны профили высотой 500 мкм и шириной от 2,0 мм до 12 мм переменной длины, с проволокой диаметром 500 мкм. Сплошные медные элементы, которые прочно связаны с рисунками проводников, могут быть нанесены непосредственно на базовую медь с использованием технологии ультразвукового соединения и интегрированы в любой слой многослойного материала с использованием базового материала FR4.Медь используется по нескольким причинам: она имеет вдвое большую теплопроводность по сравнению с алюминием и, таким образом, обеспечивает быстрое рассеивание тепла без изоляции промежуточных слоев под светодиодной грелкой.

Таблица 1: Теплопроводность используемых материалов
Еще одним преимуществом меди и основного материала печатной платы FR4 являются свойства теплового расширения (Таблица 2): При соединении с керамическими светодиодами печатные платы на основе меди или FR4 обладают высокой устойчивостью к тепловым нагрузкам, которые зависят от условий окружающей среды, условий эксплуатации и других температурных циклов, например, для «интеллектуального» управления освещением.

коэффициент расширения в направлении X / Y
Таким образом, срок службы и надежность всего осветительного блока могут быть значительно увеличены по сравнению с обычной печатной платой с металлическим сердечником на основе алюминия.

Печатные платы управляют теплом

Взгляд на удельную теплопроводность показывает важность непрерывного металлического пути от источника до стока и потенциал производительности HSMtec. Медь проводит тепло в 1000 раз лучше, чем FR4. Комбинация интегрированных медных профилей с современными конструкциями печатных плат, такими как микро- и тепловизоры, позволяет напрямую контактировать с паяльной поверхностью (компонентами, радиатором) с профилями, тем самым избегая узких мест в тепловом тракте.

Термически оптимизированная структура слоев также обеспечивает быстрое распространение тепла и, таким образом, поддерживает всю термическую концепцию. В случае очень маленьких корпусов светодиодов заполненные микропереходы обеспечивают прямое металлическое соединение с теплопроводными медными элементами, которые могут быть прикреплены примерно на 60 мкм ниже верхнего слоя печатной платы.

2. Тепловые свойства плат с металлическим сердечником и теплопроводность FR4 со встроенной медью

По сравнению с Thermovias, которые размещаются непосредственно под нагревательными пластинами, например, можно без проблем паять заполненные микропереходы.Основываясь на различных эмпирических исследованиях, Хойзерманн смог получить всевозможные знания в области регулирования температуры и высокого тока на печатной плате. Основным преимуществом HSMtec по сравнению с альтернативными решениями является использование недорогого стандартного материала FR4 в дополнение к производству в стандартном производственном процессе. Также можно использовать этот процесс для создания самонесущих многомерных печатных плат с медным проводом

С помощью фрезерования надрезов в заранее определенных точках изгиба отдельные сегменты могут быть приведены в желаемую ориентацию с помощью любой регулировки угол наклона.Толстая медь, интегрированная с профилями и проводами, выдерживает токи до 500 А. Это разумная альтернатива решениям на печатных платах, которые обеспечивают сплошные медные слои толщиной до 500 мкм, или дорогостоящим решениям IMS, в которых используются массивные алюминиевые сердечники. в качестве теплоносителя вместо обычного основного материала развертывают.

Конструкция позволяет проводить большое количество тепла и / или высокие токи до 500 А непосредственно внутри печатной платы. Кроме того, вся архитектура не требует кабелей, разъемов или других механических соединений.Это не только увеличивает надежность приложения, но и увеличивает срок его службы. Для успешной реализации креативного дизайна освещения с помощью мощных светодиодов необходимо тесное сотрудничество между заказчиком и производителем печатных плат: уже на этапе разработки концепции необходимо оптимально согласовать весь тепловой дизайн — от печатной платы до корпуса светильника. . Различные варианты прототипов и термический анализ позволяют индивидуальные решения.

Свойства и характеристики теплопроводных материалов FR4 обеспечивают большую универсальность по доступной цене.По этой причине их часто используют для изготовления печатных плат. Поэтому для нас нет ничего необычного в том, чтобы посвятить им статью в нашем блоге.

FR-4 — это стандарт, установленный NEMA (Национальная ассоциация производителей электрооборудования) для композитных материалов из затвердевшей эпоксидной смолы и стекловолокна. Код 94V-0 есть на всех печатных платах FR-4. Это гарантирует, что огонь не распространяется и быстро погаснет, если материал загорится. Температура стеклования (Tg) для High TG или HiTG составляет от 115 до 200 ° C в зависимости от метода производства и используемых смол.FR-4 использует бром, химический элемент, и так называемый тугоплавкий галоген. Он заменяет G-10, другой композитный материал, который в большинстве случаев является менее огнестойким. FR-4 также предлагает хорошее соотношение между огнестойкостью и весом. FR-4 High CTI: сравнительный индекс слежения (сопротивление слежения) превышает 600 вольт. FR-4 без медной фольги: идеально подходит для изоляционных плат, моделей и держателей печатных плат. Более подробную информацию о свойствах этих различных материалов можно найти далее в этой статье.

Что объединяет наш мир

Свойства основных материалов для электронных сборок.

Что такое «основной материал»?

Отдельными компонентами типичного основного материала являются клей, материал основы и проводящий слой. FR4, наиболее широко используемый базовый материал, изготовлен из адгезивной эпоксидной смолы, а основной материал — из скрученных стекловолокон, которые вплетены в стеклоткань. «FR» означает «огнестойкость» и, таким образом, указывает на незаменимую огнестойкость материала.«4» обозначает определенный тип FR. Существуют также типы «FR2» и «FR3», которые в настоящее время практически не используются, и «FR5» с более высокой термостойкостью, как «FR4».

Препреги и ламинаты

При производстве основного материала FR4 стеклоткань с эпоксидной смолой сначала пропитывается. В результате получается «препреги», искусственное слово, обозначающее «Предварительно пропитанный» и указывающее на то, что матрица эпоксидной смолы высохла, но еще не затвердела.

Каждый препрег состоит из стеклоткани одного типа, который обозначается числом, например, «106», «1080», «2116» или «7628».Этот вид обозначения ранее относился к толщине препрега очень обязывающей. 106 имел толщину около 50 мкм, 1080 около 60 мкм, 2116 ок. 115 и 7628 прибл. 180 мкм.

Современная потребность в безопасном, но в то же время недорогом прессовании многослойных материалов привела к появлению различных вариантов препрега, которые отличаются толщиной смоляного покрытия. По-прежнему существуют препреги со стандартным содержанием смолы, но теперь также со средним и высоким содержанием смолы. Обычными идентификаторами являются «SR» для «стандартной смолы», «MR» для «средней смолы» и «HR» для «высокой смолы».С учетом всех производственных допусков толщина одного так называемого препрега 1080 в последнее время колеблется от 56 мкм (= вариант SR, нижний допуск) до 84 мкм (= вариант HR, верхний допуск).

В просторечии доступны «тонкие ламинаты» толщиной от 0,05 до 0,86 мм и «толстые ламинаты» толщиной от 0,90 до 3,2 мм. Толщина медного покрытия может составлять 5, 9, 12, 17, 35, 70, 105, 210 или 420 мкм. Нет никаких прямых физических свойств, связанных с такой толщиной меди.Обозначения взяты из англо-американской языковой области по историческим причинам только кратным или целым делителем 1 унции (= 35 мкм). Винченц, Таубе, Вимерс: печатные платы и технологии сборки. Печатные платы и сборочные технологии. Препреги и медная фольга — это сырье для электроники. ламинаты — это уже производные продукты. Кстати, эта ссылка также объясняет классическую толщину печатной платы 1,50 мм.

Технические характеристики теплопроводности FR4

В обозримом будущем FR4 и его производные. Материал стабилен, изоляция надежна, диэлектрические свойства приемлемы, затраты приемлемы, обработка налажена, а термостойкость приемлемая. Производные по существу образуются путем модификации матрицы эпоксидной смолы. После перехода на бессвинцовую электронику (~ RoHS) стало обычным делом заменять часть объема смолы минеральными наполнителями. Это задерживает увеличивающееся в зависимости от температуры расширение печатной платы по оси Z (параметр CTE (z) = «Коэффициент теплового расширения»).

В результате более высокой термостойкости, вероятность того, что печатная плата будет повреждена во время пайки. Затем говорят о «теплопроводности FR4 с более высоким значением Tg» или также о «материале с высокой Tg». Стандартное значение для FR4 составляет 130 °, более высокие значения Tg составляют 150 ° или 175 °, в зависимости от производителя материала. В общем, «Tg» ошибочно переводится как «температура стеклования». Однако имеется в виду, что структура эпоксидной смолы становится мягкой и эластичной, как только достигается значение Tg, и, следовательно, расширение по оси Z значительно увеличивается.

Событиями ошибки тогда являются трещины в соприкасающихся переходных отверстиях и / или отрывы внутренних проводящих дорожек от переходных муфт. Также могут возникать отслоения, которые приводят к частичному растворению композита прессованного материала. Следствием этого обычно является отказ модуля. Постоянная рабочая температура модуля из материала FR4 не должна превышать 95–100 ° C. Более высокое значение Tg не увеличивает длительную рабочую температуру модуля. Постоянная рабочая температура в основном зависит от матрицы эпоксидной смолы и не должна превышать 95-100 ° для материала FR4.Другой параметр — значение Td. «Td» означает «Время разложения» и описывает значение температуры, при котором материал теряет 5% своей массы из-за выделения газа / испарения.

С момента внедрения технологии SMD требования к основному материалу возросли. Уменьшение конструкции компонентов SMD также приводит к уменьшению площадей SMD на печатной плате, потому что в противном случае надежная пайка невозможна (например, скрученные компоненты, захоронение). Когда площадка SMD становится меньше, площадь, с которой эта площадка прилегает к печатной плате, также становится меньше. Простые механические нагрузки, вибрация и силы торможения или ускорения могут вызвать разрыв компонента. Пайка оплавлением дополнительно снижает адгезию между площадкой для поверхностного монтажа и печатной платой до 75%, в зависимости от типа основного материала, поверхности печатной платы и количества циклов оплавления. К сожалению, взамен меры по достижению высокой Tg часто приводят к снижению адгезии меди.Для стандартного материала сила отрыва может составлять около 2 Н / мм, а для материала с высокой Tg может упасть до 0,8 Н / мм.

Note

Узнайте о техническом качестве базовых материалов в Интернете или поговорив с производителем печатной платы. Используйте физические свойства основных материалов для своей концепции схемы. Убедитесь, что используемый основной материал обеспечивает неизменно высокое качество вашей сборки.

Тепловое сопротивление — обзор

5.2.2.3 Теплопередача внутри скважинного теплообменника и его основные влияющие факторы

В соответствии с основными принципами, обсуждавшимися ранее при работе с сильно связанными источниками тепла окружающей среды, при проектировании скважинного тепла В теплообменнике (BHE) очень важно обеспечить — рентабельным способом — подачу или отвод тепла из земли без чрезмерной разницы температур между жидким теплоносителем и окружающей землей, тем самым минимизируя разницу между T _2r и T ₂ (см. Рисунок 5.1). Эта разница температур сильно зависит от параметра, известного как термическое сопротивление жидкости относительно земли, в котором двумя основными составляющими этого сопротивления являются тепловое сопротивление между жидкостью-теплоносителем и стенкой скважины, известное как тепловое сопротивление скважины , и тепловое сопротивление окружающего грунта от стенки скважины до некоторого подходящего среднего уровня температуры, называемого тепловым сопротивлением грунта (см. Eskilson, 1987; Hellström & Kjellsson, 1998).

Термическое сопротивление грунта включает окружающий грунт от стенки скважины до некоторого эталонного уровня температуры, обычно естественной ненарушенной температуры грунта T ₂ в приложениях типа GSHP. ⁵ В этом типе применения удобно рассматривать тепловую реакцию из-за скачкообразного изменения удельной скорости закачки тепла q (Вт / м) ⁶ , заданной на единицу длины ствола скважины, и ассоциировать температуру эволюция с зависящим от времени тепловым сопротивлением заземления R _г , так что:

(5.2) Tb − T2 = qRg

, где T _b — температура в стенке скважины. Единица термического сопротивления грунта R _г — К / (Вт / м). Другим важным фактором при проектировании скважинных систем является тепловое сопротивление между теплоносителем в проточных каналах ствола скважины и стенкой ствола скважины. Тепловое сопротивление между флюидом и стенкой ствола скважины дает разницу температур между температурой флюида в коллекторе ( T _f ) и температурой у стенки скважины ( T _b ) для определенной удельной скорости теплопередачи. q (Вт / м):

(5.3) Tf − Tb = qRb

As T _f представляет реальную температуру, при которой тепловой насос фактически забирает тепло из холодного резервуара (Tf≈T2r), из комбинации уравнения (5.2) и Уравнение (5.3) легко вывести:

(5.4) T2r − T2 = q (Rg + Rb)

Следовательно, с точки зрения производительности системы, мы можем видеть, что важно минимизировать термическое воздействие на грунт, а также на состояние ствола скважины. тепловое сопротивление. Однако тепловое сопротивление грунта сильно зависит от таких факторов, как удельное тепловое сопротивление грунта (в зависимости от типа или состава грунта), которое проектировщик не может изменить.Также важно отметить, что обычно используется несколько групп скважин. Тепловое взаимодействие между соседними скважинами разовьется через относительно короткое время, что повлияет на значение R _г . Обычный подход здесь заключается в измерении с помощью так называемых методов импульсного или переходного отклика (TRT) (ASHRAE, 2002; Gehlin, 1998) индивидуального значения скважины R _г , которое затем экстраполируется путем моделирования. через соответствующие так называемые g-функции на поведение всего скважинного поля.Наконец, R _г также зависит от того, насколько интенсивно грунт использовался ранее для термической экстракции / закачки и, следовательно, от энергетического поведения системы (характеризуемого количеством часов, в течение которых система использовалась при полной нагрузке на протяжении всего нагрева. время года).

Термическое сопротивление скважины зависит от расположения проточных каналов и тепловых свойств используемых материалов. Типичные значения, наблюдаемые при полевых испытаниях, варьируются от 0,01 К / (Вт / м) для разомкнутой коаксиальной схемы до примерно 0.25 К / (Вт / м) для одинарных U-образных труб из бентонитового раствора с плохим тепловым контактом с окружающей стенкой скважины. Для типичной скорости теплопередачи 50 Вт / м соответствующие перепады температур, которые могут возникнуть из-за термического сопротивления ствола скважины, будут варьироваться от 0,5 ° C до значений вплоть до 12,5 ° C, что потенциально может очень существенно повлиять на работу системы. Чтобы свести к минимуму R _b , для обеспечения лучшей теплопередачи используются заполняющие материалы (например, бентонит, бетон и т. Д.) В скважинах, залитых раствором.Однако в заполненных водой скважинах — очень популярных на севере Европы — теплопередача вызывает естественную конвекцию в скважинной воде и в окружающем проницаемом грунте. Этот эффект возможен только при соблюдении определенных условий грунта и приводит к снижению общего термического сопротивления скважины.

В целом термическое сопротивление ствола скважины зависит:

•

От качества раствора

•

От материала трубы ствола скважины

•

От потока жидкости внутри ППТ если условия потока ламинарные, тепловой контакт намного хуже, чем в условиях турбулентного потока.

•

Возможное тепловое короткое замыкание между восходящими и нижними ветвями внутри BHE

Использование более высоких скоростей потока может минимизировать последний два фактора, но в результате возникает компромисс с увеличением потребности в насосах.

Наконец, при рассмотрении уравнения (5.4) можно пойти другим путем: ограничить удельную скорость отвода тепла, q . Это подход некоторых из наиболее известных стандартов для разработки мелководных геотермальных источников, таких как немецкий стандарт VDI 5450 (VDI, 2008). Здесь максимально допустимые показатели отвода тепла фиксируются в зависимости от различных почв и рабочих параметров данной системы. В первые годы внедрения BHE в Европе стандартным значением для Германии было значение 50 Вт / м (тогда как значение 55 Вт / м обычно принималось для Швейцарии).Эти значения использовались в то время при проектировании жилых зданий GSHP, и 50 Вт / м до сих пор являются практическим значением для определения размеров небольших установок. Однако из всех рассмотрений, сделанных ранее, очевидно, что система BHE не должна разрабатываться в соответствии с такими типами правил.

Экспериментальный метод определения эффективной теплопроводности печатных плат

• Х. Дж. Л. Ванлаер
• К. Дж. М. Ласанс

Доклад конференции

• 6
  Цитаты

• 197
  Загрузки

Abstract

Предлагается экспериментальный метод определения эффективной теплопроводности для плоских пластин, таких как печатные платы (PCB), с использованием аналитической модели с постоянными граничными условиями. Центральная температура нагретой горизонтально размещенной (анизотропной) печатной платы является функцией теплопроводности различных материалов, из которых состоит плата. Подгонка теплопроводности изотропной аналитической модели до тех пор, пока центральная температура не станет равной измеренной центральной температуре, гарантирует, что эта теплопроводность может быть интерпретирована как эффективная теплопроводность рассматриваемой печатной платы. Поскольку аналитическое решение требует постоянных и однородных граничных условий, особое внимание было уделено построению того же набора граничных условий в экспериментальной установке.Упаковка печатной платы материалом, у которого хорошо известны как теплопроводность λ, так и толщина c, гарантирует, что неизвестный и неоднородный коэффициент теплопередачи a будет заменен известным и однородным коэффициентом λ / c. Если снова упаковать печатную плату между двумя алюминиевыми пластинами, поддерживающими постоянную температуру, эталонная температура устанавливается на постоянное значение. И отвод тепла, и измерение температуры производились бесконтактными средствами. Калибровка и проверка устройства показали хорошее согласие с известными данными для тестовых образцов PTFE и Glass G291.Результаты сопоставлены с литературными данными.

Ключевые слова

Коэффициент теплопроводности Коэффициент теплопередачи Печатная плата Эффективная теплопроводность Число Био

Эти ключевые слова были добавлены машиной, а не авторами. Это экспериментальный процесс, и ключевые слова могут обновляться по мере улучшения алгоритма обучения.

Это предварительный просмотр содержимого подписки,

войдите в

, чтобы проверить доступ.

Предварительный просмотр

Невозможно отобразить предварительный просмотр.Скачать превью PDF.

Ссылки

1. Агарвал Р.К., Дасгупта А. и др .: 1991; «Прогнозирование теплопроводности PWB / PCB», Int. Ж. для гибридной микроэлектроники Том 14 №3.

   Google Scholar

2. Carslaw, H.S. И Джагер, Дж.К .: 1978; «Проводимость тепла в твердых телах», Oxford Press, стр. 176-186.

   Google Scholar

3. Chatenier du, F .: 1987; Philips Internal Rapport, CTB 87.34.134.

   Google Scholar

4. Дин Д.Дж .: 1985; «Тепловое проектирование электронных плат и корпусов», Электрохимические публикации, стр. 151-152.

   Google Scholar

5. Дикерсон, П .: 1967; «Удобные методы термического анализа сборок печатных плат», стр. 43, Proc. Nepcon.

   Google Scholar

6. Estes, R.C.:1988; «Соображения по тепловому расчету для приложений COB», Hybrid Circuits vol.17, стр. 49–55.

   Google Scholar

7. Lasance, C.:1993; «Управление температурным режимом электронных систем с воздушным охлаждением: новые вызовы для исследований», настоящий том.

   Google Scholar

8. Philips Research Lab 1992, личное общение.

   Google Scholar

9. Савар, Ф., Пул, Нью-Джерси, и Уиттинг, П.А.: 1990; «Стекловолоконные ламинаты для печатных плат: измерения теплопроводности и их влияние на моделирование» Журнал электронных материалов, том 19, № 12. стр.1345–1350.

   ADSCrossRefGoogle Scholar

10. Сигел Р. и Хауэлл Дж. Р. 1972; «Тепловой перенос тепла», МакГроу-Хилл, стр. 18-26.

    Google Scholar

Информация об авторских правах

© Springer Science + Business Media Dordrecht 1994

Авторы и аффилированные лица

• H.J. L. Vanlaer
• C. J. M. Lasance

1. 1.Центр производственных технологий, Филипс Н.В. Эйндховен, Нидерланды

Идеи схем теплового сопротивления для объяснения теплового потока

Основные выводы

• Один из способов представить себе теплопередачу в любой системе — это рассмотреть сопротивление тепловому потоку между горячими и холодными регионами.

• Тепловое сопротивление становится частью модели схемы для понимания и прогнозирования того, как тепло будет передаваться по системе.

• Термическое сопротивление можно рассчитать, используя теплопроводность различных материалов в системе.

Термическое сопротивление влияет на то, как тепло проходит через этот аэрогель.

Теплопередача неизбежна, когда существует разница температур между двумя областями в системе. Разница температур заставляет тепло течь между горячими и холодными регионами, но эта передача тепла не происходит мгновенно.Некоторые инженеры-теплотехники разработали полезную аналогию для размышлений о теплопередаче, известную как цепь теплового сопротивления. Если вы разрабатываете печатную плату, ИС или систему в целом, то это помогает рассчитать тепловое сопротивление в различных частях системы, чтобы помочь управлять распределением температуры.

К счастью, представление о теплопередаче так же, как и об электрическом токе, дает удобный способ увидеть, как тепло перемещается между различными областями печатной платы, ИС или другого типа системы.Каждый объект обладает некоторой теплопроводностью, которую можно использовать для расчета теплового сопротивления и прогнозирования передачи тепла между различными областями вашей системы. Давайте посмотрим, как это работает математически и концептуально.

Что такое цепь термического сопротивления?

Цепь теплового сопротивления — это один из способов схематично предсказать, как будет течь тепло в различных системах. Тепловое сопротивление объекта зависит от его теплопроводности и размеров, как определено в приведенном ниже уравнении.На принципиальной схеме показана цепь термического сопротивления, которая представляет собой тепловой аналог электрической цепи.

Схема термического сопротивления и ее аналог для теплопередачи.

На верхнем графике у нас есть ситуация, когда одна сторона объекта более горячая, чем другая, что приводит к тому, что тепло начинает передаваться через систему со скоростью q. Модель эквивалентной схемы для этой системы показана в нижней половине, где для этой системы определено тепловое сопротивление.Как и в случае с обычным резистором, мы можем определить тепловое сопротивление в этой цепи с точки зрения теплопроводности системы, точно так же, как вы определяете электрическое сопротивление по электропроводности.

Анализ теплового потока в тепловых цепях

Как и в электрической цепи, тепловые сопротивления различных элементов в вашей системе объединяются, чтобы создать эквивалентное тепловое сопротивление. Различное количество тепла будет проходить через разные ветви контура, что описывает, как тепловой поток распределяется по вашей системе.Тепловые цепи можно очень легко проанализировать с помощью закона Ома, который дает эквивалентное тепловое сопротивление и полный тепловой поток для заданного температурного градиента в системе.

Если вы можете определить области печатной платы с низким тепловым потоком (например, области с высоким тепловым сопротивлением) или чрезмерно высоким тепловым потоком (области с низким тепловым сопротивлением), есть несколько факторов, которыми вы можете управлять для регулировки теплового потока:

• Выбор подложки для печатной платы : подложка с большей теплопроводностью будет иметь меньшее тепловое сопротивление, и наоборот.Вы можете заменить подложку на другой материал (например, керамическую подложку).

• Наличие переходных отверстий, медных проводов и плоскостей. : Эти элементы обладают высокой теплопроводностью, что означает, что они имеют низкое тепловое сопротивление. Добавление или удаление этих элементов на печатной плате регулирует теплопередачу по мере необходимости.

• Группировка компонентов : Это не влияет на термическое сопротивление других областей платы, но вы можете распределить компоненты с высоким энергопотреблением, а не группировать их в одной области.Это приведет к более равномерному распределению температуры на вашей печатной плате.

Думая о равновесии

Если мы возьмем изолированную систему и установим температурный градиент между двумя областями, тепло начнет передаваться от горячих областей системы к холодным. Когда тепло начинает покидать горячую область и приближаться к холодной, температура в каждой области начинает меняться. Температура во всей системе приближается к температуре равновесия, которая одинакова во всей системе.

В электрической системе у нас должно быть что-то вроде изменения напряжения обратно к некоторому равновесному значению в системе. Рассмотрим, что происходит в разряжающемся конденсаторе; напряжение на конденсаторе похоже на разницу температур между двумя точками на печатной плате. По мере того, как заряды покидают конденсатор и рекомбинируют в другом месте цепи, напряжение на конденсаторе экспоненциально падает с течением времени, как это видно на зависимом от времени поведении, предсказанном с помощью закона охлаждения Ньютона.

По мере охлаждения температура приближается к некоторому равновесию, которое можно предсказать, зная теплопроводность, плотность и удельную теплоемкость системы (как функции от пространства). Как и в случае с температурой, разность потенциалов на нашем теоретическом конденсаторе упадет до нуля при измерении на двух пластинах. Этот переход к равновесию от начальной температуры показан на графике ниже:

Переход к тепловому равновесию в цепи теплового сопротивления с экспоненциальным дека y.

Другими словами, падение напряжения на полностью разряженном конденсаторе равномерно распределяется между двумя пластинами. Если бы вы были для измерения напряжения между пластинами, потенциалом вы бы измерить, по отношению к некоторой наземной опорной плоскости, будет равномерно распределены по всему телу конденсатора. Точно так же, если мы измеряем температуру системы в равновесии, температура также равномерно распределяется по всей системе.

При наличии источников тепла, таких как ИС в печатной плате, температура ИС создает новое равновесное распределение температуры, которое не является плоским, что легче всего визуализировать с помощью решателя 3D-поля.Этот тип инструмента рассматривает тепловыделение и передачу тепла (в том числе с помощью воздушного потока) как мультифизическую проблему и представляет результаты в числовом и визуальном виде. Затем вы можете использовать числовые данные для расчета теплового сопротивления в вашей системе и при необходимости вносить изменения в конструкцию.

Если вам нужно визуализировать, как потоки тепла в различных областях электронной системы с помощью модели цепи теплового сопротивления, вы можете использовать трехмерный решатель поля, чтобы построить карту распределения температуры в вашей системе.Когда вы добавляете этот инструмент в свой рабочий процесс, вы можете определять равновесную температуру в вашей системе и извлекать значения теплового сопротивления как часть управления теплом.

Тепловое сопротивление | Neutrium

Концепция термического сопротивления может использоваться для решения задач стационарной теплопередачи, которые связаны с последовательными, параллельными или комбинированными последовательно-параллельными компонентами. В этой статье показано, как рассчитать общее тепловое сопротивление для таких систем и как рассчитать тепловое сопротивление для практических геометрий, таких как стенка трубы.

21:

Термическое сопротивление — это сопротивление конкретной среды или системы потоку тепла через ее границы, которое зависит от геометрии и тепловых свойств среды, таких как как теплопроводность.

Точное знание теплового сопротивления данной системы или компонента системы может позволить рассчитать тепловой поток через него или температуры на его границах. Это особенно полезно при решении задач теплового проектирования в промышленности, таких как расчет теплопотерь из резервуара или выбор изоляции трубопроводов.

Сети термического сопротивления обычно используются для анализа стационарной теплопередачи. Сети с тепловым сопротивлением имеют те же функции, что и сети электрического сопротивления, используемые в электротехнике, и позволяют легко рассчитать общее тепловое сопротивление в системе, независимо от того, состоит ли она из последовательно включенных, параллельных или обоих сопротивлений.

Сопротивление последовательно

Часто приходится рассматривать передачу тепла через различные среды последовательно, одним из таких примеров является тепловой поток от газа на одной стороне плоской стенки к газу на другой стороне. Эту систему теплопередачи можно проанализировать с помощью приведенной ниже схемы теплового сопротивления.

Общее сопротивление для описанной выше системы может быть рассчитано из всех сопротивлений компонентов R _conv1 , R _wall и R _conv2 следующим образом.

После расчета общего сопротивления тепловой поток через систему можно рассчитать, зная две конечные температуры, следующим образом.

Сопротивление параллельно

Передача тепла может также происходить через сопротивление параллельно, например, потеря тепла с внешней поверхности бака будет происходить из-за механизмов конвективной и радиационной теплопередачи.

Обратное полное сопротивление для системы, показанной выше, может быть вычислено путем сложения обратных сопротивлений двух компонентов.

Это можно упростить, чтобы его можно было напрямую комбинировать с тепловыми сопротивлениями других компонентов в данной системе, что особенно важно, когда тепловые сопротивления существуют как параллельно, так и последовательно.

Комбинированное последовательное и параллельное сопротивление

В промышленных задачах теплопередачи тепловое сопротивление часто бывает как последовательным, так и параллельным. Например, потеря тепла из содержимого неизолированного резервуара будет иметь конвективное сопротивление содержимого резервуара, за которым следует сопротивление проводимости стенок резервуара последовательно, а затем конвективное и радиационное сопротивление окружающей среде параллельно.Этот пример описывается схемой теплового сопротивления ниже.

В этом случае общее сопротивление может быть вычислено путем сложения общего сопротивления для последовательного сегмента и общего сопротивления для параллельного сегмента, как описано в предыдущих разделах.

При проектировании и оптимизации промышленного оборудования часто требуется определить установившуюся температуру в некоторой точке сети теплового сопротивления, например температуру между стенкой резервуара и внутренней стороной его изоляции.

Для определения этих температур необходимо сначала рассчитать термическое сопротивление. Некоторые уравнения для расчета теплового сопротивления представлены ниже.

Сопротивление проводимости

Уравнения сопротивления проводимости для некоторых распространенных случаев приведены в таблице ниже.

9274 Сопротивление конвективной теплопередачи по следующему уравнению.