Рассчитать катет: Онлайн калькулятор: Длина стороны прямоугольного треугольника

2 )/2

Калькулятор прямоугольного треугольника

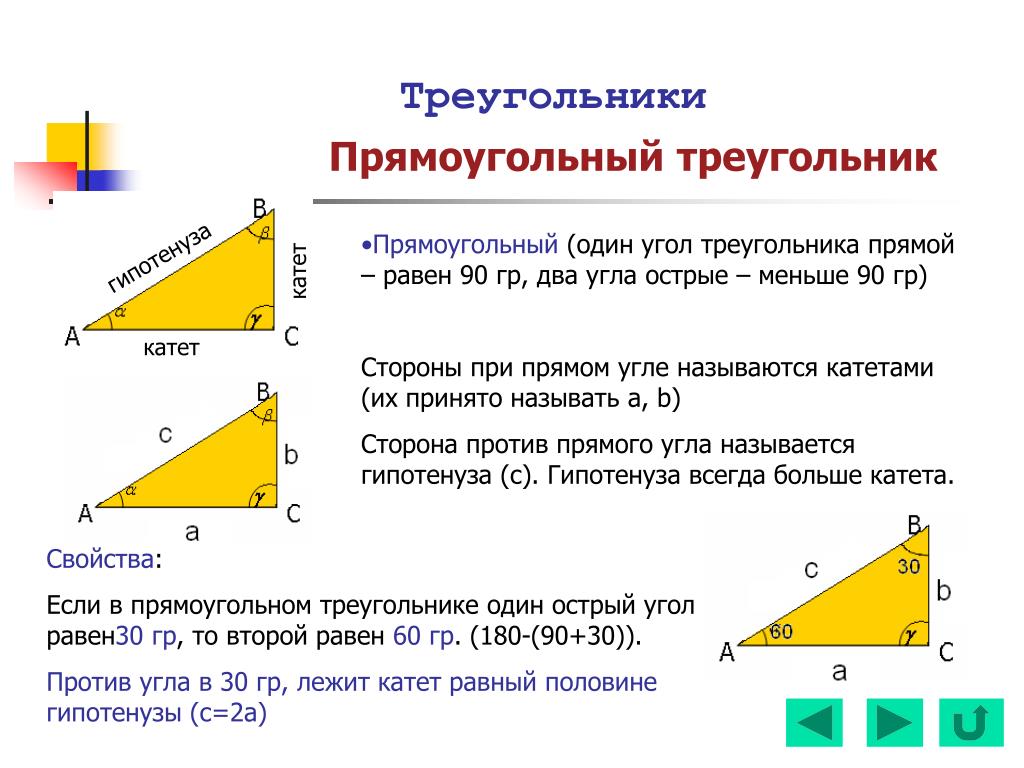
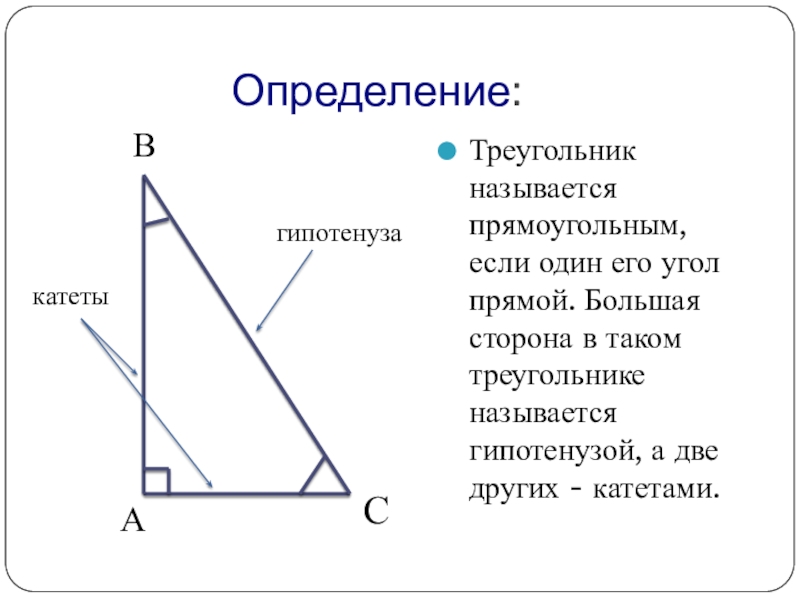
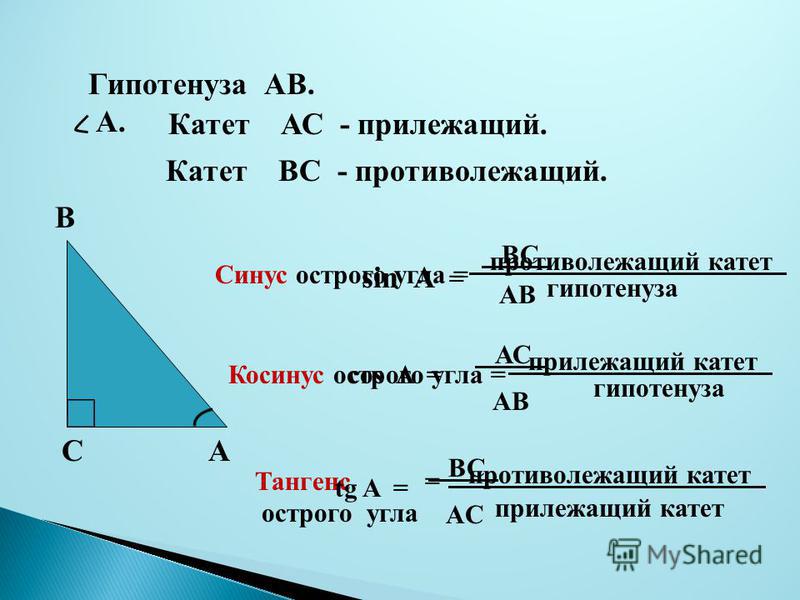
ΔABC — прямоугольный треугольник


Катеты a = BC, b = AC


Гипотенуза c = AB

Как пользоваться онлайн-калькулятором. В форме укажите известные параметры прямоугольного треугольника:

а) 2 катета,

б) катет и гипотенуза,

в) катет и противолежащий острый угол,

г) гипотенуза и острый угол.

Заполните поле «Текст с картинки». Нажмите «Решить».

Калькулятор сторон и углов треугольника

При помощи калькулятора прямоугольного треугольника можно найти гипотенузу онлайн, а также катеты, величины острых и противолежащих углов прямоугольного треугольника.

В форме калькулятора гипотенузы указываются два параметра прямоугольного треугольника онлайн: две стороны или острый угол и сторона.

Для углов имеются два поля: для градусов и для минут.

Далее заполнить поле «Текст с картинки» и нажать «Решить».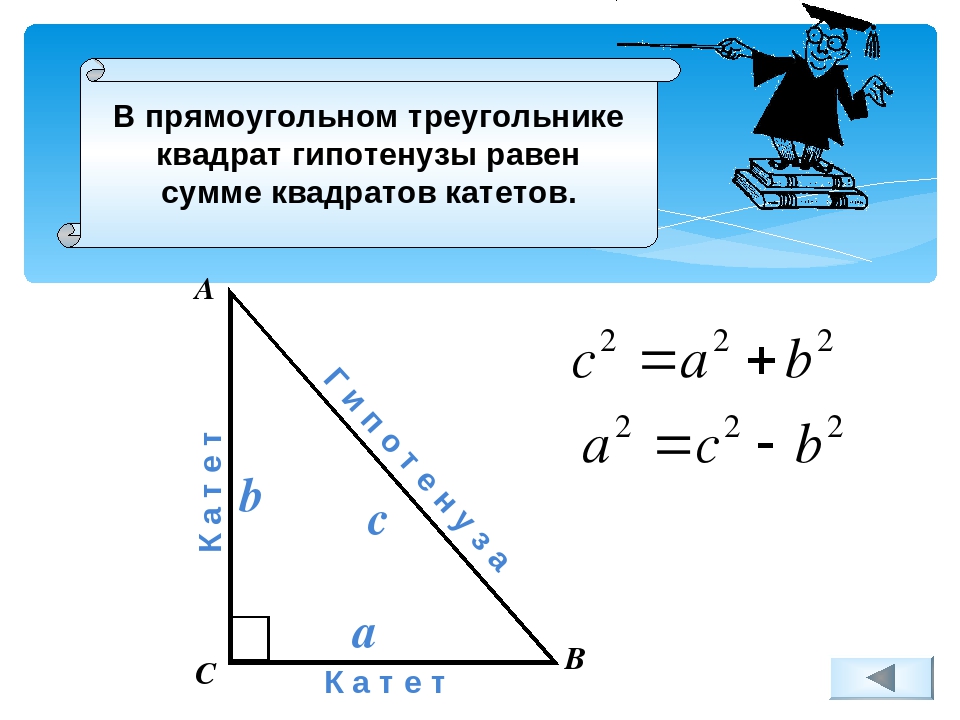 Компьютерная программа автоматически сделает расчет.

Приводятся ответы с подробными решениями, включая формулы. Для решения задач используется теорема Пифагора. Катеты и гипотенуза вычисляются через синус.

Примеры решения калькулятора прямоугольного треугольника:
1) как найти неизвестный катет или катеты, если известна гипотенуза, равная 2 см, и острый угол 20°. В поле для гипотенузы «c» указывается 2, в поле «Угол (градусов, °)» ставится 20, в поле «Угол (минут, ‘)» указывается 0. Ответ онлайн калькулятора прямоугольного треугольника: длина катетов a = 0,68 см; b = 1,88 см, острый угол B = 70°.

2) пример вычисления неизвестных сторон и острых углов прямоугольного треугольника по двум катетам или по гипотенузе и катету. Вопрос: как найти угол прямоугольного треугольника, зная его стороны, т. е. зная 2 катета или 2 стороны. Известна длина катетов a=11, b=60.

В полях для катетов «a» указывается 11, в поле «b» 60. Нажать «Решить». В ходе решения находим третью сторону – гипотенузу – и находим угол в прямоугольном треугольнике, уже зная все стороны.

Ответ калькулятора гипотенузы: гипотенуза c=61, значения углов A= 10°23′, B = 79°37′. Если даны катет и гипотенуза, то заполняются поля для катета «a» и для гипотенузы «c».

3) с помощью этого онлайн-калькулятора можно решить задачу, где требуется найти катет онлайн, или как найти гипотенузу, зная катет и угол. Например, a=3, противолежащий угол = 30°27′. В поле для катетов «a» указывается 3, в поле «Угол (градусов, °)» ставится 30, в поле «Угол (минут, ‘)» указывается 27. Ответ калькулятора углов прямоугольного треугольника: гипотенуза c = 5,92; катет b = 5,10; угол 59°33’.

Калькулятор сторон прямоугольного треугольника может найти гипотенузу по катету и углу. Онлайн калькулятор гипотенузы находит катет по гипотенузе и углу.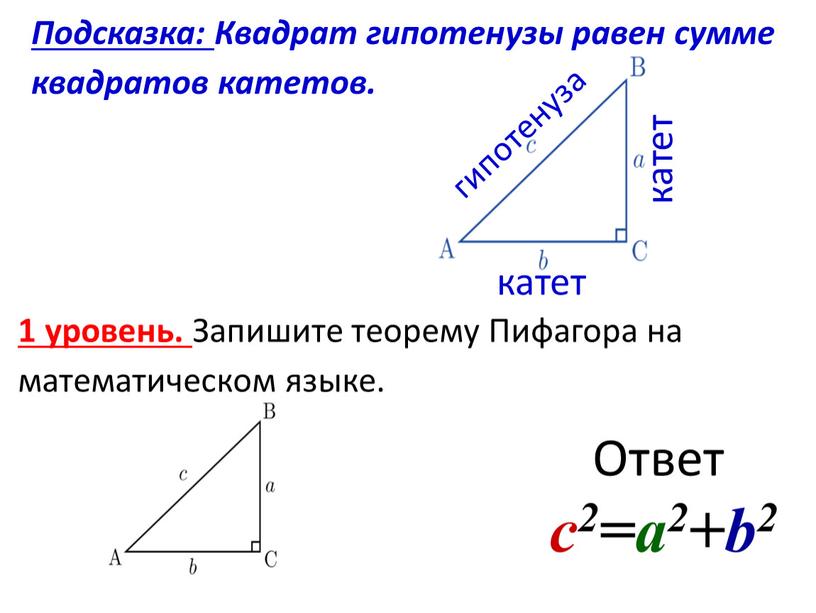

Если стоит задача, как найти катет, если известна гипотенуза и угол, то можно использовать решение прямоугольного треугольника на этой странице. Гипотенузу прямоугольного треугольника, его угол быстро вычисляет компьютерная программа. Калькулятор теоремы Пифагора может найти катет по углу и катету.

Здесь предлагаются ответы на тесты, если требуется вычислить угол по двум катетам. Расчет гипотенузы выполняется онлайн.

Вычисление гипотенузы и углов прямоугольного треугольника при помощи калькулятора катетов дает ответы на следующие тестовые задания по теме «катет и гипотенуза«:
— как найти угол прямоугольного треугольника, зная его стороны,
— узнать гипотенузу, катет прямоугольного треугольника,
— определить гипотенузу по двум катетам,
— рассчитать третью сторону прямоугольного треугольника,
— вычислить катет, если известна гипотенуза и угол,
— найти решение прямоугольного треугольника,
— определить длину гипотенузы, зная 2 катета,
— посчитать угол в прямоугольном треугольнике,
— узнать гипотенузу по катетам,
— рассчитать величину угла в градусах и минутах по катетам,
— найти длину катета по катету и углу,
— вычислить угол или углы прямоугольного треугольника онлайн,
— решить прямоугольный треугольник,
— подсчитать угол по катетам,
— найти сторону прямоугольного треугольника,
— рассчитать прямоугольный треугольник онлайн.

Катет — гипотенуза

Какую сторону треугольника нужно посчитать?

Гипотенузу


Катет

Укажите размеры:

Результат:

Решение:

Отправить ссылку в:

Треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.

Катет — это прилежащая прямому углу сторона треугольника.

Гипотенуза — это сторона треугольника противолежащая прямому углу. Гипотенуза является самой длинной стороной треугольника.

Теорема Пифагора

Квадрат гипотенузы равен сумме квадратов катетов

c^2 = a^2 + b^2

• c — гипотенуза
• a — катет
• b — катет

Как посчитать сторону прямоугольного треугольника

Гипотенуза:

c = \sqrt{a^2 + b^2}

Катеты:

a = \sqrt{c^2 — b^2}

b = \sqrt{c^2 — a^2}

Проверочные числа

Часто используют удобный приём магии чисел 3, 4, 5. 2

9 + 16 = 25

Значит треугольник со сторонами 3, 4, 5 является прямоугольным.

Похожие калькуляторы:

Как найти стороны прямоугольного треугольника

Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для гипотенузы (с):
• длины катетов a и b
• длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
• длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)

• для катета:
• длину гипотенузы (с) и длину одного из катетов
• длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
• длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
• длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
• длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:

c² = a² + b²

следовательно: c = √a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √3² + 4² = √9 + 16 = √25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

c = ^a/_cos(β) = ^b/_cos(α)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

c = ^a/_sin(α) = ^b/_sin(β)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0. 5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

a = √c² — b²

b = √c² — a²

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √5² — 4² = √25 — 16 = √9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

a = c ⋅ cos(β)

b = c ⋅ cos(α)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.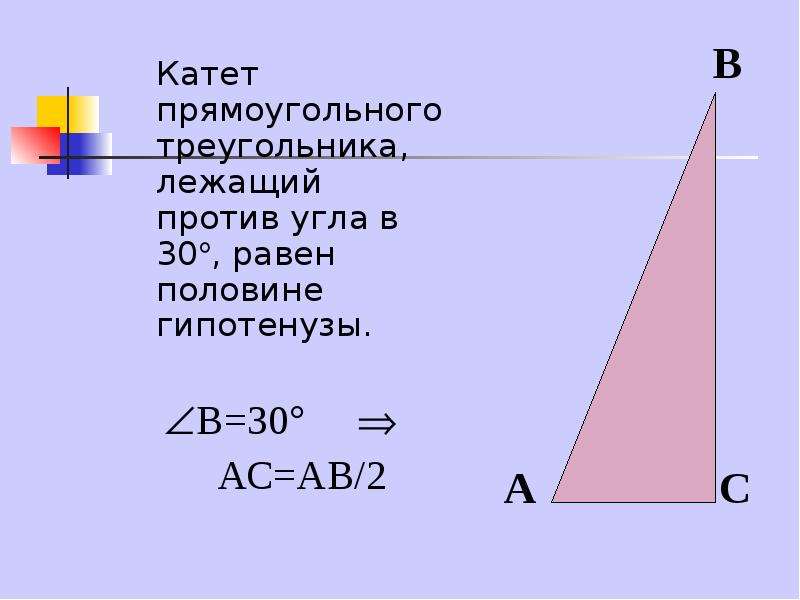 5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

a = c ⋅ sin(α)

b = c ⋅ sin(β)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

a = b ⋅ tg(α)

b = a ⋅ tg(β)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

a = b / tg(β)

b = a / tg(α)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

a = 3 / tg(35) ≈ 3 / 0.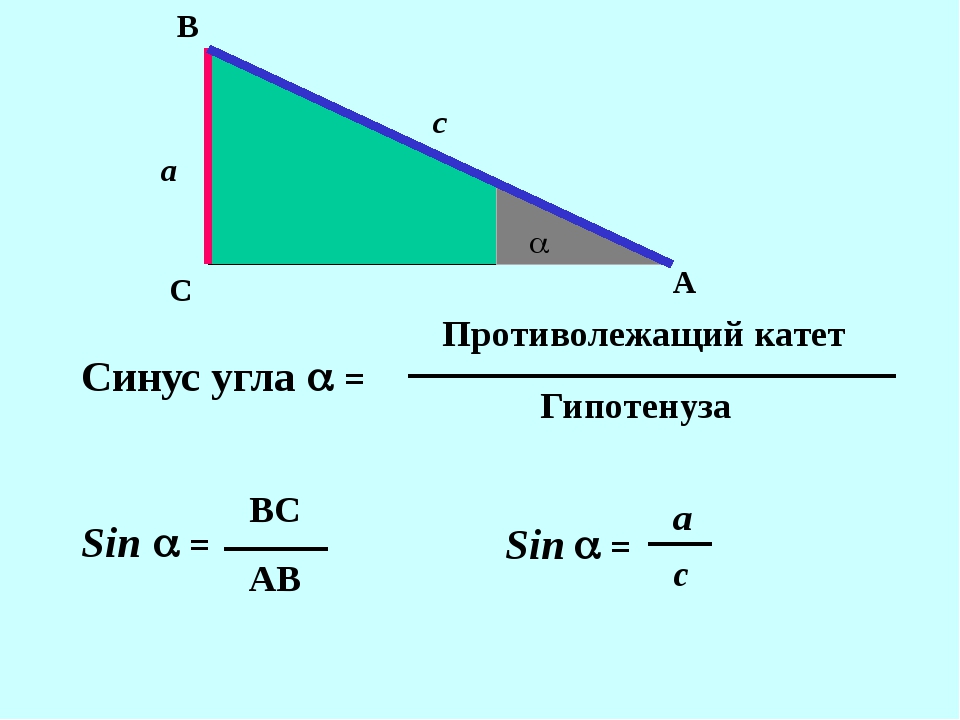 7 ≈ 4.28 см

См. также

Площадь прямоугольного треугольника: онлайн калькулятор, формулы, примеры решений

Прямоугольный треугольник встречается в реальности практически на каждом углу. Знание о свойствах данной фигуры, а также умение вычислять ее площадь, несомненно пригодится вам не только для решения задач по геометрии, но и в жизненных ситуациях.

Геометрия треугольника

В элементарной геометрии прямоугольный треугольник — это фигура, которая состоит из трех соединенных отрезков, формирующих три угла (два острых и один прямой). Прямоугольный треугольник — оригинальная фигура, характеризующаяся рядом важных свойств, которые составляют фундамент тригонометрии. В отличие от обычного треугольника стороны прямоугольной фигуры имеют собственные названия:

• Гипотенуза — самая длинная сторона треугольника, лежащая напротив прямого угла.
• Катеты — отрезки, образующие прямой угол. В зависимости от рассматриваемого угла катет может быть прилежащим к нему (образующий этот угол с гипотенузой) или противолежащим (лежащим напротив угла). Для непрямоугольных треугольников катетов не существуют.

Именно соотношение катетов и гипотенузы составляет основу тригонометрии: синусы, тангенсы и секансы определяются как отношение сторон прямоугольного треугольника.

Прямоугольный треугольник в реальности

Данная фигура получила широкое распространение в реальности. Треугольники находят применение в проектировании и технике, поэтому расчет площади фигуры приходится выполнять инженерам, архитекторам и проектировщикам. Форму треугольника имеют основания тетраэдров или призм — трехмерных фигур, которые легко встретить в повседневности. Кроме того, угольник — наиболее простое представление «плоского» прямоугольного треугольника в реальности. Угольник — это слесарный, чертежный, строительный и столярный инструмент, который используется для построения углов как школьниками, так и инженерами.

Площадь треугольника

Площадь геометрической фигуры — это количественная оценка того, какая часть плоскости ограничена сторонами треугольника.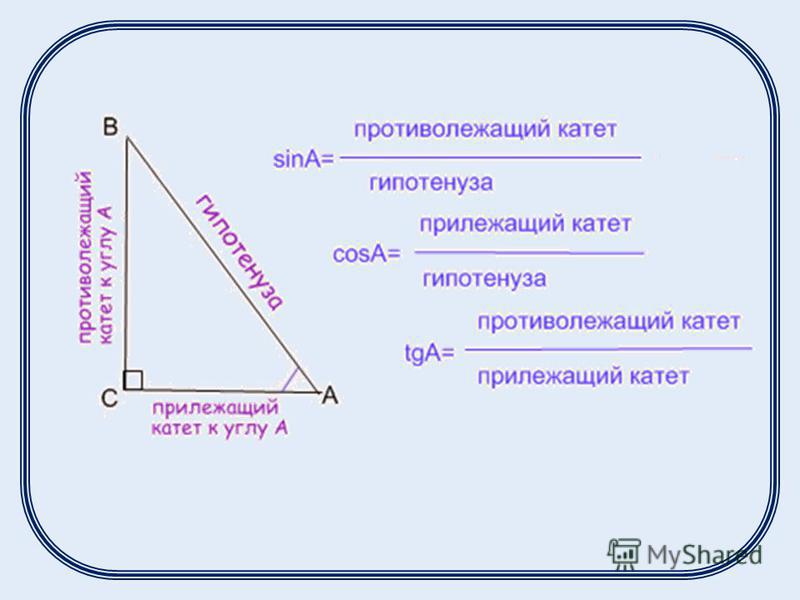 Площадь обычного треугольника можно найти пятью способами, используя формулу Герона или оперируя при расчетах такими переменными, как основание, сторона, угол и радиус вписанной или описанной окружности. Самая простая формула площади выражается как:

S = 0,5 a × h,

где a – сторона треугольника, h – его высота.

Формула для вычисления площади прямоугольного треугольника еще проще:

S = 0,5 a × b,

где a и b – катеты.

Работая с нашим онлайн-калькулятор, вы можете вычислить площадь треугольника, используя три пары параметров:

• два катета;
• катет и прилежащий угол;
• катет и противолежащий угол.

В задачах или бытовых ситуациях вам будут даны разные комбинации переменных, поэтому такая форма калькулятора позволяет вычислить площадь треугольника несколькими способами. Рассмотрим пару примеров.

Примеры из реальной жизни

Керамическая плитка

Допустим, вы хотите выполнить облицовку стен кухни керамической плиткой, которая имеет форму прямоугольного треугольника. Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:

S = 180,5

Это означает, что площадь одного элемента составляет 24,5 квадратных сантиметра или 0,01805 квадратных метра. Зная эти параметры, вы можете подсчитать, что для отделки 7 квадратных метров стены вам понадобится 7/0,01805 = 387 элементов облицовочной плитки.

Школьная задача

Пусть в школьной задаче по геометрии требуется найти площадь прямоугольного треугольника, зная только то, что сторона одного катета равна 5 см, а величина противолежащего угла составляет 30 градусов. Наш онлайн-калькулятор сопровождается иллюстрацией, на которой указаны стороны и углы прямоугольного треугольника. Если сторона a = 5 см, то ее противолежащий угол — это угол альфа, равный 30 градусов. Введите эти данные в форму калькулятора и получите результат:

S= 21,65

Таким образом, калькулятор не только вычисляет площадь заданного треугольника, но и определяет длину прилежащего катета и гипотенузы, а также величину второго угла.

Заключение

Прямоугольные треугольники встречаются в нашей жизни буквально на каждом углу. Определение площади таких фигур пригодится вам не только при решении школьных заданий по геометрии, но и повседневной и профессиональной деятельности.

что это такое, способы расчета и влияние размеров на прочность шва

Сварные металлоконструкции активно используются в самых разных направлениях жизнедеятельности: строительстве, промышленности, автомобилестроении, в быту и других областях. Чтобы конструкции были долговечными и безопасными в эксплуатации недостаточно выбрать оптимальный режим сваривания и качественные металлические заготовки.

Прочность соединительных швов непосредственно зависит от того, насколько правильно рассчитаны их параметры еще до начала сварочного процесса. Если прочность стыковых соединений зависит от ширины валика, то для угловых стыков важным нормативом является катет сварного шва.

Что в сварочном соединении обозначает катет

Лучшим способом получить выносливые и долговечные соединения изделий из металлов является их сваривание. Но состыковка отдельных деталей в цельные конструкции должна осуществляться в соответствии действующих нормативов. Смогут ли массивные и габаритные металлоконструкции выдерживать постоянные эксплуатационные нагрузки непосредственно зависит от катета сварочного соединения.

Что такое катет в сварке и какие функции он выполняет в готовых изделиях? Если рассматривать образуемый угловой сваркой стык в разрезе, то в идеале он должен воссоздавать равнобедренный треугольник. Расстояние от начала одного стыкового соединения до конца второго обозначает катет сварочного шва.

Другими словами, катет шва при сварке — это длина плоскости наибольшего треугольника с равными сторонами, который не выходит за пределы поперечного сечения.

От величины катета напрямую зависит прочность шовного соединения. Например, недостаточной прочность будет при минимальной величине катета из-за небольшой площади сечения, а при чрезмерно большом значении может возникнуть деформация металла по причине увеличенного объема наплавки. Также большая величина влечет за собой повышенный расход электроэнергии и используемых при сваривании материалов.

Типы сварочных соединений и геометрия угловых стыков

Место сцепления деталей, созданное посредством расплавления и последующего остывания металла, называют сварочным швом. В зависимости от конфигурации и варианта расположения заготовок швы разделяются на стыковые и угловые. Первая разновидность в одной плоскости соединяет торцами два элемента, вторая — образует угол между свариваемыми заготовками.

Основными геометрическими параметрами угловых соединений являются:

• толщина, состоящая из глубины провара и выпуклой части;
• ширина — размер наваренной между двумя деталями линии в поперечном сечении;
• высота — расстояние между началом стыка и гипотенузой;
• выпуклость — длина линии, проведенной от гипотенузы до самой высокой и выпуклой точки шовного стыка;
• корень — максимально удаленная от поверхностей стыкуемых элементов часть наплавления;
• глубина провара — определяется по заполненному металлом зазору без учета выпуклости;
• катет шва при сварке — расстояние между кромкой соединения и поверхностью второй заготовки.

Есть ряд специалистов, особенно начинающих сварщиков, которые попросту не понимают, что такое катет сварного шва и считают, что для повышения прочности стыка достаточно увеличить объем наплавки. Но такое мнение является большой ошибкой и чем больше металла наплавлять, тем высшие риски перегрева материала.

Расчет катета

Чтобы избежать ошибок и изготовить действительно качественную, способную выдерживать высокие нагрузки металлоконструкцию необходимо предварительно рассчитать какой должен быть катет сварного шва.

От этого показателя непосредственно зависят прочностные характеристики создаваемых изделий, в частности:

• нельзя увеличивать наплавление, поскольку от этого существенно изменяются в худшую сторону прочностные характеристики;
• если повысить ширину охвата, то сразу же расширяется площадь нагревания и соответственно расплавляется большее количество металла. В результате это становится причиной деформации всей конструкции;
• слишком большие ширина и высота сварных швов существенно повышают количество расходуемых материалов, а если речь идет о массовом производстве, то такие затраты попросту недопустимы;
• при сваривании заготовок разной толщины очень важно определить значение катета, и рассчитывать его нужно с учетом геометрических параметров детали, которая тоньше;
• слишком узкие шовные соединения не обладают должной прочностью и понижают качество всей конструкции. Особенно важно это в случаях, когда готовые изделия будут подвергаться постоянным нагрузкам.

Расчет катета сварного шва позволяет еще до начала сварочных работ определить какими прочностными свойствами будет обладать металлоконструкция. Кроме этого и с финансовой точки зрения наличие таких показателей необходимо. Вплоть до копейки можно рассчитать себестоимость работ, обеспечивая экономию на расходе электроэнергии и комплектующих.

Критерии выбора катета сварочного стыка

Длина сварного шва вычисляется в отдельности для каждого из подлежащих спайке элементов. Полученный результат напрямую зависит от ряда характеристик:

• толщина соединяемых друг с другом деталей;
• материал, из которого выполнены заготовки;
• тип соединения — одно- или двухстороннее в зависимости со скольких сторон проваривается угол;
• технические характеристики расходных материалов, в частности проволоки и электродов.

Для обеспечения нужной прочности важно правильно определить размеры валика. Недопустимой считается завышенная или минимальная длина сварного шва, она должна соответствовать действующим нормам.

Влияние катета на геометрические параметры углового шва

Кроме прочностных показателей катет углового сварного шва влияет на правильность геометрии создаваемых соединений:

• когда одна из сторон стыкового соединения слишком вытянута, то это является признаком того, что только на одну заготовку наложен расплав, а вторая заготовка прикреплена плохо. Поэтому важно чтобы с обеих сторон катеты были одинаковыми. Дефекты такого характера возникают из-за смещения дуги вправо или влево;
• растянутый и плоский валик указывает на то, что расплавившийся металл хаотично растекся по поверхности деталей. Это тоже считается браком, образующимся из-за чрезмерно короткой дуги;
• при очень коротких катетах на стыковых соединениях образуются большие выпуклости. Такие дефекты возникают при длинной дуге, металл при этом застывает сверху и даже при небольших нагрузках сразу же появляются трещины.

Чтобы получить идеальный вариант сварного шва наряду с контролем за геометрическими параметрами нужно также соблюдать технологию сваривания. Дуга после зажигания должна находиться строго по центру создаваемого стыка. Оптимальной считается длина дуги, когда она составляет 1-1,5 исходя от диаметра электрода.

Скорость движения и форму сварочной ванны необходимо контролировать. Ванна должна иметь овальную форму. Если визуально она напоминает круг или слишком вытянута, то это прямой признак неправильности сварного процесса. Непровары металла возникают вследствие высокой скорости перемещения электрода. Когда скорость очень низкая, то высока вероятность появления прожогов металла.

Каждый из указанных выше факторов крайне важен в сварочном процессе. Но при соблюдении техники сваривания и зная каким должен быть размер катета сварного шва не сложно выполнить качественные стыковочные соединения, обеспечивающие надежность и долговечность любой конструкции.

Как провести расчеты катета сварочного стыка

Что такое катет шва в сварке и каким образом он влияет на технические характеристики полученных в процессе сваривания изделий можно понять по выше изложенному материалу. Поэтому сомнения по поводу проведения вычислений этого параметра лишние.

Значения сварочных соединений и показатели их прочности в промышленных условиях вычисляют математическим путем, применяя для этого специальные формулы.

В бытовых условиях измерения можно выполнить с помощью готового специализированного шаблона-катетометра. Это состоящий из калиброванных пластин прибор. Перпендикулярно к линии стыка поочередно прикладывают каждую пластинку, результат определяется по той, которая плотнее всех прилегает к поверхностям.

Если под рукой у мастера нет катетометра, то вместо него можно использовать угольник и штангенциркуль. К одной из заготовок прикладывается угольник, при этом его вершина должна опираться в вершину полученного при сваривании валика. К другой вершине нужно опустить щуп штангенциркуля. Измерение катета сварного шва выполняется по вылету щупа, который равен вычисляемой длине.

Здесь следует обратить внимание на то, что при наличии длинных шовных валиков на проверку уходит достаточно много времени, а сами измерения не обладают высокой точностью.

Другие способы визуального вычисления катета

Существует несколько эффективных методов как измерить катет сварного шва, сущность которых состоит на физических принципах. К таковым относят ультразвуковой контроль, дефектоскопирование, просвечивание стыков рентгеновскими и гамма-лучами, радиографический способ.

Капиллярным методом и магнитным зонированием иногда проводят определение катета сварного шва. Но такие способы весьма затратные, поскольку для контроля необходимы дорогостоящие реактивы и аппаратура.

Есть еще специальные компьютерные программы, позволяющие быстро выполнить необходимые расчеты и получить точные показатели. В данном случае потребуется предварительно измерить геометрические характеристики сварочного стыка. Сделать это можно с помощью универсальных шаблонов визуальным путем:

• прибор Красовского УШК-1. Применяют для замеров зазоров между свариваемыми деталями, габаритов стыковых, тавровых и нахлесточных соединений;
• измерительное устройство УШС-2. Это комплект шаблонов, которыми катет сварки определяется по выпуклой гипотенузе с диапазоном 4-14 миллиметров;
• прибор УШС-3. Процесс измерения с ним более сложный. С его помощью проверяются показатели углов разделки швов, высота сварного шва и смещение между соединяемыми элементами;
• шаблон, оснащенный измеряющим Маршака-Ушерова УШС-4. Предназначен для проведения промеров корня шва, углов и размера катета. Среди всех приборов считается наиболее универсальным.

Не стоит недооценивать определение «что такое катет сварного шва», потому что от него прямо зависит качество работ, прочность соединительного стыка и всей конструкции в целом.

Визуальный метод получения геометрических значений не требует особых навыков и применения дорогостоящего оборудования, а также является наиболее финансово доступным способом проверки сварных изделий на соответствие поставленному техническому заданию.

Как рассчитать катет с учетом толщины исходного материала

Чтобы безошибочно вычислить размер катета сварного шва от толщины металла требуется линию треугольника выбирать с учетом габаритов самих изделий, вида и положения спая.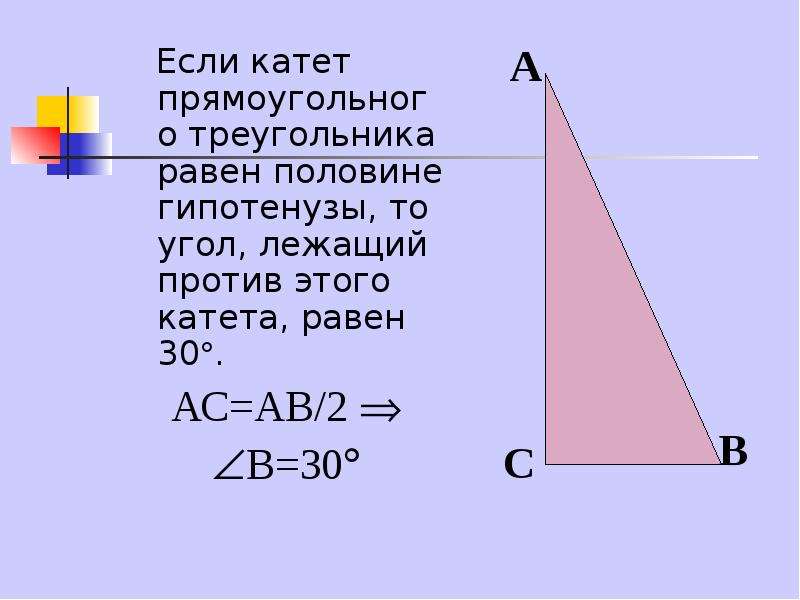 Для каждой детали индивидуально происходит подбор, но при этом обязательно необходимо руководствоваться общими принципами.

Чтобы соединение было надежным и основательным, обе одинаковые по длине стороны треугольника должны находиться перпендикулярно одна к другой.

Сами спаи могут быть разными:

• стыковые: с односторонним, криволинейным, V или X-образным скосом, или вообще без скоса кромок;
• выполненные внахлест;
• торцевые;
• угловые: не меньше 30° должен быть угол, двух- или односторонние с ровными кромками, с двумя или одним скошенным краем;
• тавровые: со скосами (одним или двумя) или без них, с прямым или острым углом, одно- и двухсторонние.

Среди перечисленных выше типов состыковок расчет катета сварного шва от толщины металла допустим только для тавровых, нахлесточных и угловых.

Если необходимо состыковать разные по габаритам элементы, то следует катет сварного шва принимать по наименьшей толщине свариваемых деталей.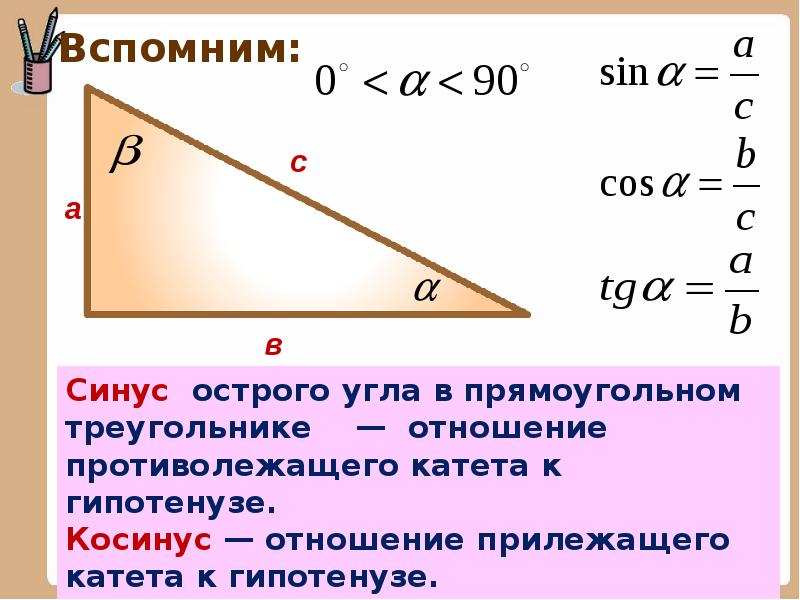

В случаях, когда сильным нагрузкам сваренная конструкция подвергаться не будет, то габариты шовного соединения можно определить по толщине материала. Например, при соединении элементов с толщиной каждого около 4-5 мм приблизительный катет не должен превышать 4 миллиметров. Если заготовки более толстые в пределах 5-6 мм, то максимальным показателем является 5 мм.

Вычисление размеров катета важно на предприятиях и заводах при серийном производстве металлоконструкций. Имея в наличии необходимые значения можно избежать брака, а также в разы сократить производственные затраты.

Расчет размера катета с применением математических формул

Известно множество математических способов для того как рассчитать катет сварного шва. Практически для каждого типа стыков существуют отдельные формулы и при необходимости их без особых проблем можно найти в интернете на специализированных сайтах, как собственно и таблица катетов сварных швов находится в открытом доступе для пользователей.

Если рассматривать валик как треугольник, то квадрат катета в нем аналогичен объему наплавки. Например, когда 10 мм составляет длина спая и при этом всего на 1 мм увеличен катет (К), то на целых 20% потребуется больше затратить проволоки.

При состыковке деталей толщиной до 4 миллиметров внахлест К должен равняться 4 мм. При высшем значении необходимо вычислить от толщины 40% и добавить 2 мм к полученному результату.

Но перед тем как выбрать катет сварного шва нельзя забывать о том, что угловые швы бывают нескольких разновидностей:

• нормальные, на которых нет вогнутых и выпуклых участков. В данном случае катет аналогичен толщине металла;
• вогнутые. Здесь катет сварного шва минимальный и составляет 0,85;
• выпуклые. Чтобы узнать какова оптимальная толщина сварного катета расчет осуществляется по формуле: К = S x cos45°. Символ S обозначает ширину спая, а cos45° — это постоянная величина, составляющая 0,7071;
• специальные, в которых треугольник валика не разносторонний.

Чтобы с максимальной точностью вычислить катет сварочного шва в зависимости от толщины металла одних только математических действий будет недостаточно. Особое значение отводится текучести свариваемого металла и технологии, посредством которой проводятся сварочные работы.

Тем, кто не может выполнить быстрые расчеты и затруднятся как выбрать катет сварного шва таблица 1 в разы упростит работу.

Для материалов с другими пределами текучести металла при необходимости рассчитать минимальный катет сварного шва таблица 2 также будет полезной для применения в работе.

ВАЖНО! Полученный при математических вычислениях результат необходимо дополнительно сверить с выдвигаемыми к геометрии шовных соединений требованиями ГОСТа 5264-80, ГОСТа 11543-75 и другими нормативными материалами.

Как вычислить размер катета для соединения 1 м

При выполнении сварочных работ в домашних условиях достаточно измерить превышающую толщину материала на 1-1,15 мм сторону и примерно определить по ней катет сварного шва, таблица с готовыми параметрами также станет хорошим помощником начинающим сварщикам. Но выполненные таким образом расчеты довольно условные, основанные на предпосылках.

Работающим на крупных промышленных предприятиях профессиональным сварщикам не нужно объяснять, что такое катет при сварке шва и какова его важность. Главной целью проектных расчетов при массовом производстве объектов и конструкций из металлических сплавов является определение подходящего размера спая по отношению к конкретным показателям осевого напряжения и растяжения материала.

Для расчета размера наплавленной присадки соответственно нагрузки на растяжение применяют следующую формулу: L = F/ ρ x [ρ], в которой L – длина наплавленного спая, F — будущая нагрузка на сварочное соединение, которой шов будет подвергаться, Ρ — максимально допустимая нагрузка на стык в процессе эксплуатации готового изделия.

Для вычисления по осевому напряжению приемлемой протяженности существует другая формула:
L = F/0,7K x ρ

Как определить катет сварного шва из этой формулы? Путем простых математических действий можно вывести новую формулу, по которой
К = 0,7 х L х ρ

Учитывая то, что нам необходимо определить габариты катета для одного метра шовной наплавки, то конечный результат будет
К = 0,7 х ρ

Если внимательно проанализировать приведенный порядок расчета, очевидным становится вывод — размер катета напрямую зависит от значений допустимой нагрузки на соединительный шов. Узнать допустимые нормы нагрузок при сваривания разными методами можно с помощью специальных таблиц.

Уже на этапе разработки проектной документации необходима толщина сварочного шва, расчет показателя выполняется с учетом:

• класса и разновидности сварки;
• марки используемых электродов;
• допустимой действующими нормами нагрузки;
• показателей осевого напряжения и растяжения;
• высоты усиления сварного шва.

На основании этих значений создается чертеж соединительного стыка, уточняются размеры и технические характеристики стыкуемых элементов. Также в процессе проектирования конструкции исчисляется катет шва по наименьшей толщине свариваемых деталей, что дает возможность оптимизировать себестоимость и повысить качество сварочного процесса.

ГОСТ катетов стыковых швов

Чтобы в процессе эксплуатации металлоконструкции выдерживали возлагаемые на них нагрузки все присутствующие на них шовные соединения должны соответствовать нормативным показателям.

Основным документом, регламентирующим размеры сварных соединений, а также типы и характеристики конструктивных элементов металлоизделий является ГОСТ.

Здесь четко указано, что при необходимости состыковать разные по толщине детали соединять их можно таким же образом, как и заготовки с равной толщиной. Только при этом разница между двумя показателями не должна превышать нормативных значений.

В одном из пунктов ГОСТа обусловлены допустимые смещения кромок по отношению друг к другу и установлены четкие параметры смещений в соответствии толщины заготовки. В приложении к документу описаны все возможные минимальные размеры катетов, которые в обязательном порядке следует учитывать при сваривании металлоконструкций.

Последствия неправильного вычисления сварного катета

Начинающие сварщики довольно часто припускаются ошибок в проведении расчетов, вследствие чего получают неправильные значения размеров катета. В случаях изготовления простых конструкций незначительные отклонения не представляют никакой опасности. Когда же ошибки допущены при создании габаритных несущих конструкций, то последствия могут быть непоправимыми. Поэтому задача первостепенной важности при сварочных работах — с безупречной точность рассчитать параметры стыков и в частности катет сварочного шва (что это такое более детально описано выше).

Любой излишек наплавления по линии соединения понижает прочность, вызывает разбрызгивание расплавленного металла, образование наплывов на поверхности деталей, а также повышает расход электродов и электроэнергии.

Но самой большой проблемой неверно выполненных расчетов является то, что даже при незначительных нагрузках конструкция начнет разрушаться и дальнейшая ее эксплуатация будет невозможной.

Как проверить качество шва и сварочных работ

Чтобы сварное соединение получилось надежным и прочным недостаточно только правильно рассчитать параметры катета. Важно также строго соблюдать технологию сваривания и следить, чтобы по всей протяжности швы были однородными и равномерными.

Существует несколько способов как проверить катет сварного шва на прочность и долговечность. Самыми популярными и часто применяемыми являются два метода:

• разрушающий. На специальных макетах проводятся разного рода испытания, по результатам которых определяется прочность стыков и конструкций в целом. Это могут быть повышенные механические нагрузки, химические, металлографические и другие исследования;
• неразрушающий. Этот способ контроля включает визуальный осмотр соединения, исследования с использованием магнитных волн, ультразвука и другого специализированного оборудования.

Визуальный контроль не требует особых навыков и наличия дорогостоящих приборов. Но его недостаточно для того, чтобы обнаружить присутствующие дефекты и неточности. Избежать образования на сварочном шве изъянов можно, если соблюдать при его создании некоторые правила:

• в месте сваривания не должно быть сквозняка и сильного ветра, поскольку это первые причины возникновения пор в соединительном стыке;
• сварочный ток превышать нельзя — это нарушает структуру металла;
• в зависимости от толщины металла необходимо правильно выбирать зазор;
• дугу лучше всего использовать короткую;
• при работе с постоянным током нельзя допускать чтобы на металл или электроды попадала вода;
• следить за тем, чтобы на всей протяженности шва одинаковой была его ширина. Даже при малейших отклонениях неравномерно будут распределяться нагрузки и возрастают риски появления трещин и полного разрушения сварочного стыка;
• контролировать глубину провара, она должна быть равномерной. В противном случае могут возникнуть внутренние трещины;
• правильно подбирать электроды для сварки. Касается это как диаметра, так и состава металлического стержня. Для выпуклых валиков подойдут электроды, которые при расплавлении образуют вязкую и густую консистенцию. Если расплав очень жидкий, то линия получится вогнутой.

От режима работы во многом зависит качество сварки и форма шовного соединения. Если нужно увеличить глубину и уменьшить ширину шва, то достичь этого можно при повышении скорости передвижения электрода. Когда наоборот глубину необходимо уменьшить и ширину сделать больше, то просто следует изменить напряжение.

Придерживаясь этих простых рекомендаций в сочетании с правильно выполненными расчетами можно не сомневаться в качестве и высоких прочностных показателях сварочного стыка.

Профессиональные сварщики на крупных производственных объектах до миллиметра определяют геометрические параметры и технические характеристики будущего шва. Но если нарушать сварочные технологии и игнорировать контрольные проверки, то даже самые точные расчеты шовных соединений не обеспечат гарантии качества сварных конструкций.

Интересное видео

как измерить, рассчитать и выбрать

В профессиональном строительстве при возведении металлоконструкций, а также при создании различных транспортных средств, которые обладают большой массой, многие соединения сталкиваются с очень высокими нагрузками. Чтобы их выдержать, следует сделать не только качественное соединение, но и рассчитать его параметры, чтобы при создании он приобрел максимальную прочность. Катет сварного шва является наиболее коротким расстоянием от плоскости соединяемой заготовки №1 до границы углового соединения, которое расположено на плоскости заготовки №2.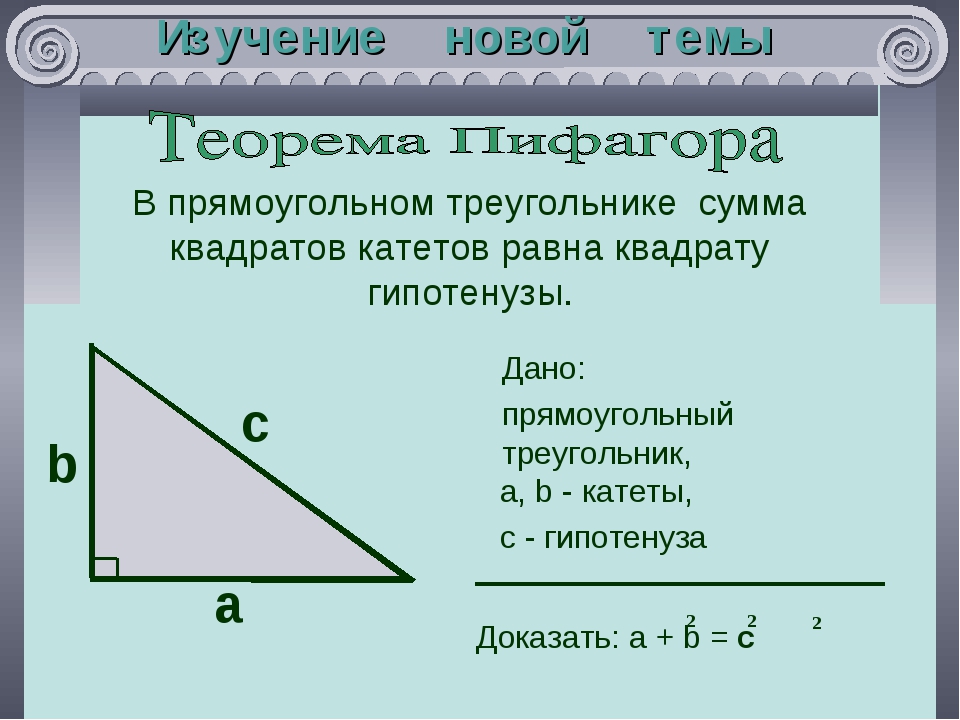 Иными словами, катет шва при сварке – это катет самого большого условного равнобедренного треугольника, который можно вписать в поперечное сечение.

Данный параметр имеет прямое отношение к тому, насколько крепким будет шов. Это легко объяснить увеличением площади сцепления двух деталей основного металла и наплавочного материала. Нагрузка, которая буде воздействовать, распределится равномерно по всей поверхности, так что изделие сможет выдержать больший, сильный удар и так далее. Но не всегда самый большой размер будет лучшим вариантом. В сварочном деле необходимы тонкие расчеты нагрузок, чтобы не допустить перенапряжение металла. При увеличенном катете может согнуться сама деталь, что приведет к невозможности ее использования.

При выборе данного параметра учитывается множество факторов. Это толщина заготовок, а также одинаковая она или нет. Нужно знать положение сварки и вид используемого шва. Здесь же необходимо учитывать особенности металла, с которым ведется работа. Несмотря на то, что для каждого шва катет подбирается индивидуально, имеются общие принципы его выбора. В частной сфере эта практика практически не применяется, так как нет необходимости в работе со сверх нагрузками, но все равно все стараются создать как можно большую площадь сцепления, чтобы при этом не навредить заготовке.

Когда свариваются детали с одинаковой толщиной стенок, то катет задается по кромке. Но периодически случается и так, что заготовки имеют различную толщину, благодаря чему катет сварочного шва подбирают на основании более тонкой заготовки. Правильный выбор его расположения и размерности является очень важным и ответственным делом. При грамотном подборе он сможет обеспечить максимальную мощность. Если размерность окажется меньше, чем нужно, то прочность шва будет слишком слабой. Если она окажется больше, то это может привести к деформации заготовки. Катет сварного шва должен соответствовать ГОСТ 5264-80.

Виды швов

Виды	Описание
Стыковой	Один из самых распространенных вариантов. Это простое соединение двух металлических изделий, которые подогнаны друг к другу  встык. Оно выполняется как со скосом кромок, так и без него данный тип соединения чаще всего производится в горизонтальной позиции.
Тавровой	Данная разновидность предполагает соединение заготовок, находящихся друг к другу перпендикулярно, или же «Т» образно. Шов может находиться как с одно стороны, так и с двух. Часто используют положение под наклоном, чтобы металл ванны не растекался, а находился между бортов заготовок.
Угловой	Данный тип предполагает соединение под определенным углом. Как правило, это задается особенностями конструкции. Здесь нужен скос кромок, чтобы была максимальная глубина приваривания
Внахлест	Данная разновидность предназначена для сварки листов, толщина является относительно небольшой. Проварка осуществляется с двух сторон.

Геометрия сварного шва

Рассмотрев разновидности мест, где катет может иметь свои параметры и особенности, стоит взглянуть на другие составляющие сварного соединения, которые также могут оказаться важными.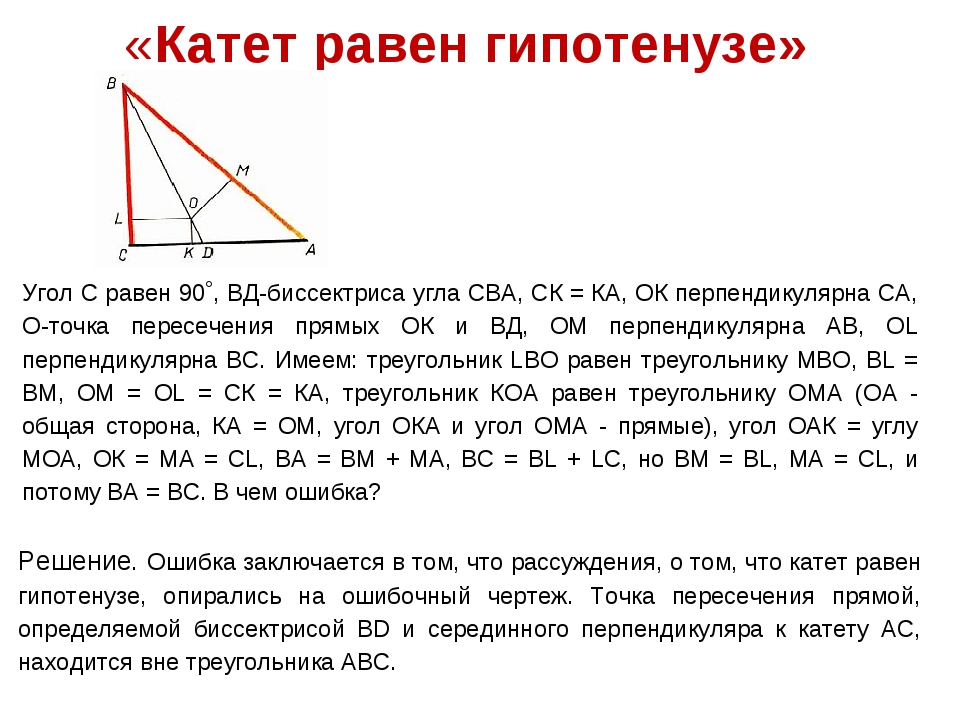 Многие величины взаимозависимы, но некоторые можно доработать уже после создания шва. К примеру, высота валика всегда может стать меньше при обтачивании, если это необходимо. Основные параметры выглядят следующим образом:

Схема обтачивания сварного шва

• E – ширина полученного шва;
• T – толщина созданного шва;
• B – зазор между свариваемыми деталями;
• H – глубина залегания области проварки;
• S – толщина используемой заготовки;
• Q – размер выпуклой части.

Для углового соединения они несколько отличаются, так как здесь другое геометрическое положение. Тем не менее, важность из значения не становится меньше. Здесь выделяют:

Схема углового соединения

• K – катет шва;
• A – Величина толщины углового шва, к которой относится величина расчетной высоты и выпуклости;
• Q – выпуклость наплавленной области;
• P – расчетная высота, что должна соответствовать перпендикулярной линии, которая проводится из места наиболее глубокого проплавления к гипотенузе наибольшего прямого треугольника, который вписан во внешнюю часть шва.

Свойства

Разобравшись с тем, что такое катет сварного шва, следует отметить свойства, которыми должно обладать соединение. В первую очередь это однородность и равномерность наплавленного валика. Это легко определиться, так как здесь может применяться даже визуально-измерительный контроль сварных швов, самый простой и доступный из них. Высота валика должна быть примерно одинаковой по всей поверхности. Это же касается и его ширины, так как в этом случае нагрузки на нем будут распространяться равномерно. Если будет какое-либо послабление, то вероятность поломки возрастает именно в этом месте.

Однородность состава обеспечивает лучшее скрепление. Как правило, различные марки металла очень плохо свариваются и чем больше различий в составе, тем хуже будут скреплены заготовки. Для высокого качества соединения следует знать, какие электроды выбрать для сварки инвертором, или другим удобным способом. Также следует рассчитать правильное геометрическое расположение шва, чтобы у него был максимальный охват скрепляемых деталей.

Не менее важным параметром является глубина проварки. Если заготовки будут соединены не по всей возможной площади, то они не смогут выдерживать максимальные нагрузки. В профессиональной сфере рассчитывается каждый параметр соединения, чтобы придать конструкции максимальную прочность. Здесь нужно знать, как рассчитать катет сварного шва, чтобы он приобрел требуемые параметры и как провести сварку.

Выбор катета шва

Расчет катета сварного шва совершается под каждое отдельное соединение. Чтобы правильно выбрать его, требуется знать параметры свариваемых деталей. Прочность здесь будет зависеть от толщины соединения и его длины. Основным параметром выбора и расчета является длина, так как от этого зависит прочность. Слишком большая длина приведет к увеличению расхода материалов, а также деформации заготовки.

Схема чтения длины катета сварного шва

На практике применяются разнообразные шаблоны, которые проверены опытом предыдущих сварщиков. Для каждого типа соединения, в зависимости от размера заготовки и положения, подбирают готовые размеры.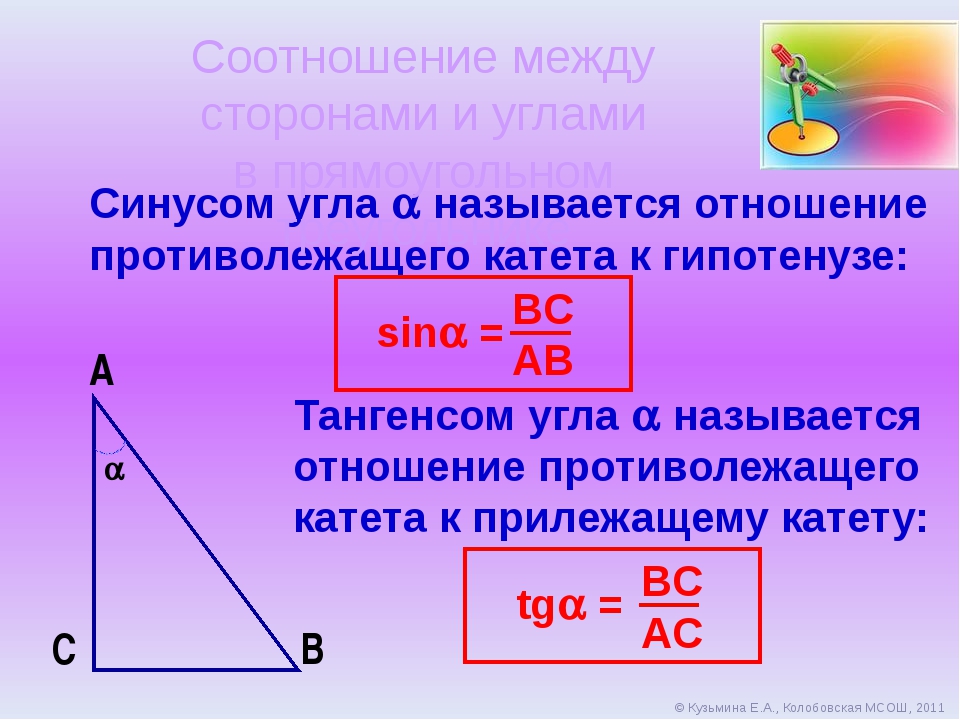

Как измерить катет сварного шва

Разобравшись с тем, как выбрать катет сварного шва, необходимо узнать, как правильно провести его измерения. Это требуется для того, чтобы проконтролировать полученный результат. Размер искомого значения определяется по обыкновенным геометрическим законам. Для этого требуется вычислить катет максимально возможного треугольника, вписанного в продольное сечение соединения. Итоговый размер катета соединения и будет искомой величиной.

Схема определения катета сварного шва

Как рассчитать катет сварного шва

В каждом случае, расчет проводится по-разному, в зависимости от имеющихся условий. К примеру, для определения нахлесточных соединений листов, толщина которых составляет менее 4 мм, катет стараются делать равным по толщине самих листов. Если же толщина листов составляет больше 4 мм, то здесь берется 40% от толщины металла и добавляется 2 мм. Таким и должен быть максимальный катет сварного шва.

Калькулятор прямоугольного треугольника | Найдите a, b, c и угол

Найти недостающую сторону или угол проще простого, чем с помощью нашего замечательного инструмента — стороны прямоугольного треугольника и калькулятора углов. Выберите два заданных значения, введите их в калькулятор, и оставшиеся неизвестные будут определены в мгновение ока! Если вам интересно, как найти недостающую сторону прямоугольного треугольника, продолжайте прокручивать, и вы найдете формулы, лежащие в основе нашего калькулятора.

Как найти стороны прямоугольного треугольника

Есть несколько методов получения длин сторон прямоугольного треугольника.В зависимости от того, что дано, вы можете использовать разные отношения или законы, чтобы найти недостающую сторону:

1. Учитывая две стороны

Если вы знаете две другие стороны прямоугольного треугольника, это самый простой вариант; все, что вам нужно сделать, это применить теорему Пифагора:

a² + b² = c²

• , если отрезок a является недостающей стороной, затем преобразуйте уравнение к форме, когда a находится на одной стороне, и извлеките квадратный корень:

  a = √ (c² - b²)

• , если участок b неизвестен, то

  b = √ (c² - a²)

• для гипотенузы c отсутствует, формула

  c = √ (a² + b²)

2. Заданный угол и гипотенуза

Примените закон синусов или тригонометрии, чтобы найти длины сторон прямоугольного треугольника:

3. Заданный угол и одна ножка

Найдите недостающую ногу с помощью тригонометрических функций:

• a = b * tan (α)

• b = a * tan (β)

4. Заданная площадь и одна нога

Как мы помним из основной формулы площади треугольника, мы можем вычислить площадь, умножив высоту и основание треугольника и разделив результат на два. Прямоугольный треугольник — это частный случай разностороннего треугольника, в котором одна ножка является высотой, а вторая ножка — основанием, поэтому уравнение упрощается до:

площадь = а * б / 2

Например, если мы знаем только площадь прямоугольного треугольника и длину участка a , мы можем вывести уравнение для других сторон:

• b = 2 * площадь / а
• c = √ (a² + (2 * площадь / a) ²)

Как найти угол прямоугольного треугольника

Если вы знаете, что один угол отличается от прямого, вычисление третьего угла несложно:

Учитывая β : α = 90 - β

Для α : β = 90 - α

Однако, если заданы только две стороны треугольника, определение углов прямоугольного треугольника требует применения некоторых основных тригонометрических функций:

для α

• sin (α) = a / c , поэтому α = arcsin (a / c) (обратный синус)
• cos (α) = b / c , поэтому α = arccos (b / c) (обратный косинус)
• tan (α) = a / b , поэтому α = arctan (a / b) (арктангенс)
• cot (α) = b / a so α = arccot ​​(b / a) (обратный котангенс)

и для β

• sin (β) = b / c , поэтому β = arcsin (b / c) (обратный синус)
• cos (β) = a / c , поэтому β = arccos (a / c) (обратный косинус)
• tan (β) = b / a , поэтому β = arctan (b / a) (арктангенс)
• cot (β) = a / b so β = arccot ​​(a / b) (обратный котангенс)

Как решить прямоугольный треугольник с одной стороной?

Чтобы решить треугольник с одной стороной, вам также понадобится , один из непрямоугольных углов . В противном случае это невозможно:

1. Если у вас есть гипотенуза , умножьте ее на sin (θ) , чтобы получить длину стороны , противоположной углу.
2. Или же умножьте гипотенузу на cos (θ), чтобы получить сторону, примыкающую к углу.
3. Если у вас есть сторона без гипотенузы, смежная с углом , разделите его на cos (θ) , чтобы получить длину гипотенузы .
4. Либо умножьте эту длину на tan (θ), чтобы получить длину стороны, противоположной углу.
5. Если у вас есть угол и сторона , противоположная , вы можете разделить длину стороны на sin (θ) , чтобы получить гипотенузу .
6. Или разделите длину на tan (θ), чтобы получить длину стороны, примыкающей к углу.

Как найти недостающую сторону прямоугольного треугольника? Как найти угол? Пример

Давайте покажем, как найти стороны прямоугольного треугольника с помощью этого инструмента:

1. Предположим, мы хотим найти недостающую сторону, заданную площадь и одну сторону. Выберите нужный вариант из раскрывающегося списка . Это третий.
2. Введите указанные значения . Например, площадь прямоугольного треугольника равна 28 кв. Дюйм, а b = 9 дюймов.
3. Наш калькулятор сторон и углов прямоугольного треугольника отображает недостающие стороны и углы! Теперь мы знаем, что:

• a = 6,222 дюйма
• c = 10,941 дюйм
• α = 34,66 °
• β = 55,34 °

Теперь давайте проверим, как работает поиск углов прямоугольного треугольника:

1. Обновите калькулятор. Выберите нужный вариант . Предположим, что у нас есть две стороны, и мы хотим найти все углы. Вариант по умолчанию — правильный.
2. Введите длину стороны . В нашем прямоугольном треугольнике гипотенуза равна 13 дюймов, а катет a = 5 дюймов.
3. Отсутствует сторона и углы . В нашем примере b = 12 дюймов, α = 67,38 ° и β = 22,62 °.

Сколько линий симметрии у прямоугольного треугольника?

Если прямоугольный треугольник равнобедренный (т.е., его две негипотенузные стороны имеют одинаковую длину) он имеет одну линию симметрии . В противном случае треугольник будет иметь без линий симметрии .

Может ли прямоугольный треугольник иметь равные стороны?

Нет, у прямоугольного треугольника все 3 стороны не могут быть равны , так как все три угла также не могут быть равны, , поскольку один должен быть 90 ° по определению. Однако у прямоугольного треугольника две стороны, не являющиеся гипотенузой, могут быть равны по длине. Это также будет означать, что два других угла равны 45 °.

Все ли прямоугольные треугольники похожи?

Не все прямоугольные треугольники похожи на , хотя некоторые могут быть такими же. Они похожи, если все их углы имеют одинаковую длину или если соотношение двух сторон одинаково.

Гипотенуза треугольника. Калькулятор

С помощью этого калькулятора гипотенузы вы быстро найдете эту самую длинную сторону прямоугольного треугольника. Если вы хотите знать, что такое гипотенуза прямоугольного треугольника, как ее найти и что такое гипотенуза формулы треугольника, вы найдете ответ ниже с простым примером, чтобы прояснить ситуацию.Не ждите больше, попробуйте этот калькулятор гипотенузы!

Какая гипотенуза у треугольника

Гипотенуза — это самая длинная сторона прямоугольного треугольника . Это сторона, противоположная прямому углу (90 °). Длину гипотенузы можно найти, например, из теоремы Пифагора.

Гипотенуза треугольника, формула

В этом калькуляторе гипотенузы реализовано несколько формул — таким образом мы убедились, что он подходит для различных сценариев, с которыми вы можете столкнуться.Вы можете найти гипотенузу:

1. Даны две ветви прямоугольного треугольника

Используйте теорему Пифагора, чтобы вычислить гипотенузу от сторон прямоугольного треугольника.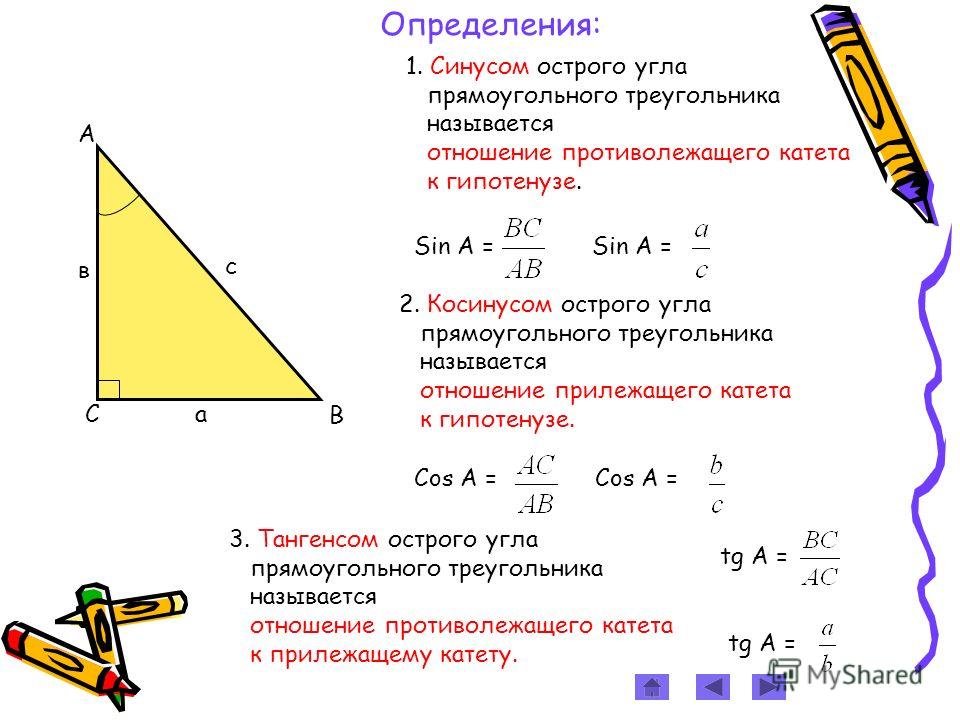 Извлеките квадратный корень из суммы квадратов:

2. Заданный угол и одна ножка

3. Заданная площадь и одна нога

Так как площадь прямоугольного треугольника равна a * b / 2 , то

• c = √ (a² + b²) = √ (a² + (площадь * 2 / a) ²) = √ ((площадь * 2 / b) ² + b²)

Как найти гипотенузу прямоугольного треугольника с помощью этого калькулятора гипотенузы?

Давайте посчитаем, какой длины должна быть лестница, если мы хотим спасти котенка с 10-футовой крыши.Калькулятор помогает найти длину лестницы от земли до края крыши, но не забывайте о части лестницы, которая должна выходить за край!

1. Выберите вариант, необходимый для ваших расчетов . Мы знаем, что наша крыша имеет высоту 10 футов и что самый безопасный угол для лестницы составляет ~ 75,5 °. Из раскрывающегося списка данного поля выберите вариант: угол ∡ и одна сторона .
2. Измените единицы на футы .

3. Введите указанные значения .Наша нога и имеет длину 10 футов, а угол α между лестницей и землей равен 75,5 °.

4. Появляется длина лестницы, которая является нашей гипотенузой прямоугольного треугольника ! Это равно 10,33 фута.

   .

   Также отображаются угол β = 14,5 ° и отрезок b = 2,586 фута. Вторая опора также является важным параметром, поскольку она говорит вам, насколько далеко лестница должна быть удалена от стены (или, скорее, от края крыши). Общий принцип, о котором следует помнить, — это правило 4: 1 — на каждые четыре фута вертикальной высоты ступенька лестницы должна отодвигаться на одну ногу от стены.

Всегда ли самая длинная сторона гипотенузы?

Да, гипотенуза всегда является самой длинной стороной , но только для прямоугольных треугольников. В равнобедренном треугольнике две равные стороны называются ногами, а в равностороннем треугольнике все стороны называются просто сторонами.

Что делать, если гипотенуза противоположная?

Если гипотенуза противоположная, то вы рассматриваете неправильный угол — вы не можете использовать тригонометрию с прямым углом треугольника.Рассмотрим один из других углов, и противоположная сторона будет стороной, которая не образует этот угол.

Что такое теорема об угле гипотенузы?

Теорема об угле гипотенузы — это способ проверить, совпадают ли два прямоугольных треугольника с или нет. В нем говорится, что если два прямоугольных треугольника имеют одинаковую гипотенузу и острый угол, они конгруэнтны.

Откуда произошло слово гипотенуза?

Слово гипотенуза происходит от древнегреческого hypoteinousa , что означает «вытягивание под (прямым углом)».Это, в свою очередь, происходит от hypo- «под» и teinein «растягивать». Еще за что надо благодарить древних греков!

Как решить прямоугольный треугольник только с гипотенузой?

Вы не можете решить прямоугольный треугольник, используя только гипотенузу . Это связано с тем, что две другие стороны и углы все еще не определены, и поэтому треугольник может иметь множество форм.

Правило ног

— математический способ

Правило отрезка (или теорема о среднем геометрическом отрезке ) связывает длину каждого отрезка прямоугольного треугольника с отрезками, проецируемыми ими на гипотенузу.

Разделите прямоугольный треугольник ( ABC ) по его высоте ( h ) на два меньших прямоугольных треугольника ( CAD и CDB ).

В каждом прямоугольном треугольнике катет ( a или b ) представляет собой среднее геометрическое между гипотенузой ( c ) и проекцией этого катета на него ( n или m ).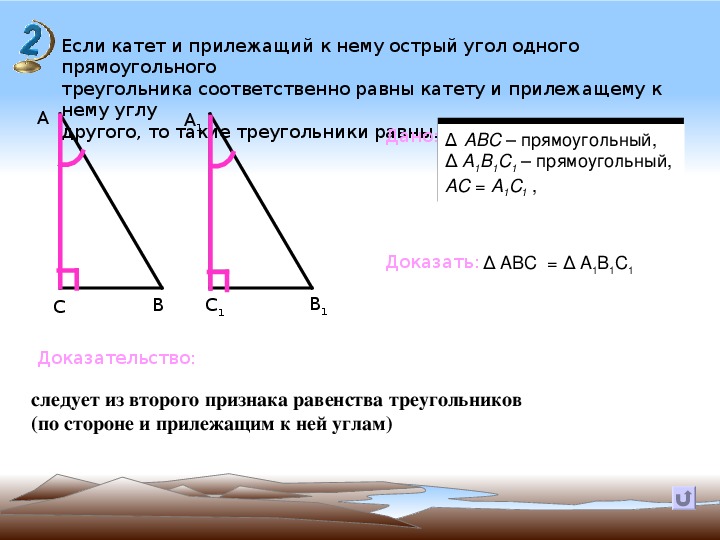

Основное приложение правила отрезка — вычислить отрезки ( a и b ) прямоугольного треугольника из сегментов проекций на гипотенузу ( n и m ) и последний ( c ).Если мы знаем длину катетов и длину гипотенузы, мы можем вычислить периметр прямоугольного треугольника.

Упражнение

1. Найдите длину катетов прямоугольного треугольника ABC , в котором проекции катетов на гипотенузу равны n = 2 см и м = 8 см. Это отрезки, на которых высота h (или высота) делит гипотенузу.
2. Найдите периметр прямоугольного треугольника ABC .

Решение:

1. Применяя теорему о геометрическом среднем (отрезке) (или правило отрезка), мы можем найти длину отрезков, если нам известны длины двух сегментов.

   Гипотенуза — это сумма двух отрезков: c = n + m = 2 + 8 = 10 см.

2. Зная длину катетов и гипотенузу, мы можем найти значение периметра:

Связь между ножками и гипотенузой

Теорема Пифагора

Теорема Пифагора , также известная как теорема Пифагора, является фундаментальным соотношением в евклидовой геометрии между тремя сторонами прямоугольного треугольника (2 катета и гипотенуза).Эту теорему можно записать в виде следующего уравнения:

Теорема о среднем геометрическом

Теорема о среднем геометрическом (или теорема о высоте гипотенузы) связывает высоту ( h ) треугольника и катеты двух треугольников, подобных основному ABC , путем нанесения высоты h на гипотенуза, утверждая, что в каждом прямоугольном треугольнике высота ( h ) относительно гипотенузы является средним геометрическим из двух проекций катетов на гипотенузу ( n и m ).

Калькулятор прямоугольного треугольника | Pi Day

Чтобы использовать калькулятор прямого угла, просто введите длины любых двух сторон прямоугольного треугольника в верхние поля. Затем калькулятор определит длину оставшейся стороны, площадь и периметр треугольника, а также все углы треугольника.

Как найти площадь и стороны прямоугольного треугольника

Сделай сам

Если нам известны только две стороны прямоугольного треугольника, мы можем использовать эту информацию, чтобы найти третью сторону, площадь и периметр треугольника, и все углы треугольника.Удивительно, правда? Давайте посмотрим, как мы найдем каждую из этих частей.

Как найти недостающую сторону прямоугольного треугольника

Чтобы найти недостающую сторону прямоугольного треугольника, мы используем знаменитую теорему Пифагора.

Нам нужно быть немного осторожными, чтобы знать, на какой стороне мы находимся. У прямоугольных треугольников два катета и гипотенуза, которая является самой длинной стороной и всегда пересекает прямой угол. Когда мы пытаемся найти гипотенузу, мы заменяем наши две известные стороны на a и b .Неважно, какой отрезок — a , а какой — b . Затем мы решаем для c , складывая квадраты значений a и b и извлекая квадратный корень из обеих частей.

Когда мы пытаемся найти один из отрезков, мы вводим известный отрезок для a и известную гипотенузу для c . Затем мы решаем для b , используя простую алгебру (вычитаем значение a , возведенное в квадрат с обеих сторон, затем извлекаем квадратный корень из обеих сторон).

Как найти площадь прямоугольного треугольника

Чтобы найти площадь прямоугольного треугольника, нам нужно знать только длину двух катетов. Гипотенуза нам вообще не нужна. Это потому, что ноги определяют основание и высоту треугольника в каждом прямоугольном треугольнике. Таким образом, мы используем общую формулу площади треугольника (A = основание • высота / 2) и заменяем на и b на с основанием и высотой . Итак, наша новая формула для площади прямоугольного треугольника: A = ab / 2.

Как найти периметр прямоугольного треугольника

Чтобы найти периметр или расстояние вокруг нашего треугольника, нам просто нужно сложить все три стороны вместе. Если мы знаем только две стороны, нам нужно сначала использовать теорему Пифагора, чтобы найти третью сторону.

Как найти углы прямоугольного треугольника

Чтобы найти углов прямоугольного треугольника, мы используем тригонометрию. Это не так сложно, как кажется.Нам просто нужно найти одну специальную кнопку на наших портативных калькуляторах. Для начала нам нужно знать все длины сторон, поэтому, если мы их еще не знаем, мы сначала воспользуемся теоремой Пифагора, чтобы найти их.

Когда у нас есть все стороны, мы определяем, какой угол мы собираемся найти. Затем берем сторону, противоположную этому углу, и делим ее на длину гипотенузы, которая равна стороне c . Это даст нам значение от 0 до 1. Теперь нам просто нужно найти кнопку ARCSIN на нашем калькуляторе, которая часто обозначается как SIN ^-1 .Нахождение ARCSIN нашего десятичного значения дает нам угол. Убедитесь, что калькулятор настроен на угловой, а не на радианный режим.

Мы можем повторить этот процесс, чтобы найти другой неизвестный угол в треугольнике, еще раз разделив его противоположную сторону на гипотенузу и взяв ARCSIN.

Или мы могли бы продемонстрировать еще больше знаний о треугольнике, используя вычитание, чтобы найти его, поскольку мы знаем, что внутренние углы треугольника должны составлять в сумме 180 °.Вычитание только что найденного угла из 180 ° и последующее вычитание известного прямого угла (90 °) также даст нам третий угол.

Этот калькулятор отлично подходит для получения всей этой информации всего с двух сторон прямоугольного треугольника, но попытаться найти стороны, углы, площадь и периметр самостоятельно без этого — интересная задача. Затем вы можете использовать его, чтобы проверить наши ответы.

Калькулятор равнобедренного треугольника — Расчет высокой точности

[1] 2021/04/25 21:30 Мужской / 50-летний уровень / Самостоятельно занятые люди / Очень /

Цель использования

Попытка подсчитать, сколько пригодно для использования масло я оставил в цилиндрическом (горизонтальном!) баке.Требуется для вычисления углов треугольника по известной гипотенузе (радиус круга) и высоте треугольника (уровень масла). Получилось удовольствие. Осталось еще 195 литров! (заменяем бак).

[2] 2021/04/21 10:12 Мужчина / Уровень 30 лет / Инженер / Очень /

Цель использования

Слишком долго не ходил в школу. Изготовление стола из эпоксидной смолы, необходимого для подрезки стальных ножек, пока смола влажная. Вырисовал ножки для прямоугольной основы, забыл некоторые геометрические доказательства.Смотрел их и вручную делал расчеты. Проверил с помощью этого калькулятора -> получилось с такими же точными числами и углами. Хороший инструмент для проверки, не ленитесь и полагайтесь на технологии, которые сделают все за вас. Вот почему у нас есть манекены, которые не могут решать математические уравнения Facebook.

[3] 2021/04/17 22:19 Женщина / 60 лет и старше / Пенсионер / Очень /

Цель использования

Пошив шторки для нашей горки для муниципального бассейна. Это пирамида, состоящая из 4-х треугольников.Стороны легко измерить, углы нужны.

Комментарий / запрос

Отлично и быстро. Спасибо.

[4] 2021/04/05 04:56 Женщина / Уровень 40 лет / Другое / Очень /

Цель использования

Рассчитать размер детской палатки для двора 🙂

[5] 2021/03/02 23:20 Женский / До 20 лет / Старшая школа / Университет / Аспирантка / Очень /

Цель использования

Быстрее решать дела

[6] 2021/02/26 02:15 Мужчина / Уровень 30 лет / Инженер / Очень /

Цель использования

Игра с периметром: отношения диаметров многоугольников с увеличивающимся числом сторон.Наблюдая, как отношение приближается к пи, когда многоугольник становится более круглым.

[7] 2021/02/10 22:40 Женщина / уровень 30 лет / Офисный работник / Государственный служащий / Очень /

Цель использования

Пытаюсь найти длины сторон, когда я знаю основание 48 дюймов и угол основания 30 градусов

[8] 2021/02/09 14:38 Мужчина / уровень 40 лет / Офисный работник / Государственный служащий / Очень /

Цель использования

Требуется дизайнерский угол «сделай сам», доступны только определенные размеры.Спасибо за калькулятор.

[9] 2021.01.21 17:17 Мужской / Моложе 20 лет / Старшая школа / Университет / аспирант / Очень /

Цель использования

школьный персонал, сложная задача

[ 10] 21.01.2021 01:17 Женщина / Моложе 20 лет / Офисный работник / Государственный служащий / Очень /

Цель использования

Сложная вещь о сельскохозяйственных колесах

Калькулятор равнобедренного треугольника — Решите любую ногу или Уголок

Введите любые два известных значения для равнобедренного треугольника, чтобы вычислить длину ребер, высоту, углы, площадь, периметр, внутренний радиус и радиус описанной окружности.

Решение:

α = 33,557 ° | 0,5857 рад

тупой равнобедренный треугольник

Что такое равнобедренный треугольник?

Равнобедренный треугольник — это треугольник, у которого есть два ребра или ножки одинаковой длины.Третий край называется основанием.

Два угла, примыкающие к основанию, называются базовыми углами, а угол, противоположный основанию, называется вершинным углом.

Поскольку ножки имеют одинаковую длину, углы основания также идентичны.

Типы равнобедренных треугольников

Существует четыре типа равнобедренных треугольников: острый , тупой , равносторонний и правый .

Острый равнобедренный треугольник — это треугольник с углом при вершине менее 90 °, но не равным 60 °.

Тупой равнобедренный треугольник — это треугольник с углом при вершине более 90 °.

Равносторонний равнобедренный треугольник — это треугольник с углом при вершине, равным 60 °. Равносторонний треугольник — это особый случай, когда все углы равны 60 ° и все три стороны равны по длине. Попробуйте наш калькулятор равностороннего треугольника.

Правый равнобедренный треугольник — это треугольник с углом при вершине, равным 90 °, и углами основания, равными 45 °.У нас есть специальный калькулятор прямоугольного треугольника для вычисления этого типа треугольника.

Как рассчитать длину ребер равнобедренного треугольника

Зная высоту или высоту равнобедренного треугольника и длину одной из ног или основания, можно вычислить длину других сторон.

Определите длину основания

Используйте следующую формулу, чтобы найти длину базовой кромки:

b = 2a² — h²

Длина основания b равна 2, умноженному на квадратный корень из катета a в квадрате минус высота h в квадрате.

Решите длину ноги

Используйте следующую формулу, чтобы найти длину ног:

a = h² + (b ÷ 2) ²

Длина участка a равна квадратному корню из высоты h в квадрате плюс основание b , разделенное на 2 в квадрате.

Как рассчитать углы равнобедренного треугольника

Учитывая любой угол в равнобедренном треугольнике, можно решить другие углы.

Решите базовый угол

Используйте следующую формулу, чтобы решить базовый угол:

α = 180 ° — β2

Угол основания α равен 180 ° минус угол при вершине β , деленный на 2.

Решите угол при вершине

Используйте следующую формулу для определения угла при вершине:

β = 180 ° — 2α

Угол при вершине β равен 180 ° минус двукратный угол основания α .

Как рассчитать площадь и периметр

Учитывая стороны равнобедренного треугольника, можно определить периметр и площадь, используя несколько простых формул.

Решить периметр

Решите периметр равнобедренного треугольника по следующей формуле:

р = 2а + Ь

Таким образом, периметр p равен 2-кратному отрезку a плюс основание b .

Полупериметр Solve

Учитывая периметр, вы можете решить полупериметр. Полупериметр s равен половине периметра.

s = p2

Решить область

Чтобы найти площадь, используйте формулу Герона:

Т = s (s — a) (s — a) (s — b)

Формула Герона утверждает, что площадь T равна квадратному корню из полупериметра s , умноженному на полупериметр s минус отрезок a умноженный на полупериметр s минус a умноженный на полупериметр s минус b .

Работа с нагрузкой на ноги — конструктор строительных лесов

Scaffold Designer может рассчитать нагрузки на опоры для строительных лесов. Таблица нагрузок на опоры рассчитывает постоянную нагрузку, динамическую нагрузку и общую нагрузку для каждой опоры на чертеже лесов на основе размера, высоты, местоположения, материалов, распорок и других переменных факторов.

Примечание: Это диалоговое окно предназначено для использования в качестве справочного инструмента. Для более точного расчета нагрузки проконсультируйтесь с сертифицированным специалистом.

Доступ к экрану нагрузки на опору

1. Выберите отсек

2. Выберите вкладку «Подмости» и нажмите Нагрузки на опору

. Откроется экран Нагрузки на опору .

Эта страница содержит следующее:

Детали расчета нагрузки на опоры

Конструктор лесов предоставляет общие расчеты нагрузки на опоры для чертежей. Для более точного расчета нагрузки проконсультируйтесь с сертифицированным специалистом.

Примечание: Расчет нагрузки для полностью подвешенных лесов недоступен.Нагрузки на строительные леса с некоторыми подвесными пролетами не передаются.

Общая нагрузка (на опору)

Конструктор лесов использует следующую формулу для определения нагрузки на опору:

Постоянная нагрузка + Динамическая нагрузка + Передаваемая нагрузка = Общая нагрузка

Постоянная нагрузка

Собственная нагрузка — это нагрузка на ноге только материалом Scaffold. Эта нагрузка не включает вес рабочих, дополнительные материалы или другие подобные переменные. Статическая нагрузка рассчитывается по следующей формуле:

Сумма1 + Сумма2 = Собственная нагрузка

Сумма1

Это вес всех компонентов непосредственно на каждой ножке, имеющей отвинчиватель.Сюда входят такие материалы, как вертикальные стойки (стандарты). шуруповерты, коллекторы (если применимо), поддерживаемые лестничные пролеты и т. д.

Sum2

Это 1/4 веса всех компонентов на отсеках, прикрепленных к выбранному отсеку опор, таких как доски, горизонтальные элементы, распорки и т.д.

Живая нагрузка

Живая нагрузка — это дополнительная нагрузка на опору при использовании лесов. Это включает рабочих, рабочие материалы и т. Д., Но не включает материалы строительных лесов. Живая нагрузка рассчитывается по следующей формуле:

Полезная площадь деки x единичная динамическая нагрузка = динамическая нагрузка

Полезная площадь деки

Это 1/4 площади используемых уровней деки, как определено пользователем в Диалоговое окно «Таблица нагрузки ног».

Единичная динамическая нагрузка

Это единичная динамическая нагрузка, как определено пользователем в диалоговом окне «Таблица нагрузок на опоры».

Передаваемая нагрузка

Передаваемая нагрузка — это дополнительная нагрузка на опору для соседних подвешенных опор / пролета. Подвесные ножки — это ножки без шуруповерта. Нагрузка будет перенесена на 1 и 1/2 отсека.

Пример непередаваемой подвешенной нагрузки

О подвешенных нагрузках

Некоторые подвешенные нагрузки на опоры будут передаваться на опорные опоры.Как правило, нагрузка на подвесные отсеки (отсеки без шуруповертов), непосредственно примыкающие к опорному отсеку (отсеку с шуруповертами), передается. Нагрузка на дополнительные подвесные отсеки не может быть передана. Для получения дополнительной информации см. Сведения о расчете нагрузки на опору выше.

Если чертеж содержит серию подвешенных опор, в которых нагрузка не может быть передана на опорные опоры, появится предупреждение:

Стойки с непередаваемой подвешенной нагрузкой будут выделены и показаны курсивом.Нагрузку на эти ноги необходимо переносить вручную по желанию.

Расчет нагрузок на ноги для чертежа

После создания строительных лесов на странице чертежа конструктор лесов автоматизирует расчет нагрузок на ноги на основе определенных вами параметров.

Чтобы рассчитать нагрузки на опоры для чертежа:

1. Щелкните вкладку Строительные леса , а затем щелкните Нагрузки на опоры .

Появится диалоговое окно Таблица нагрузок на ноги .

2. Щелкните текстовое поле Unit Live Load и введите соответствующую нагрузку.

3. Щелкните текстовое поле Количество используемых уровней колод и введите соответствующее количество уровней.

Оба значения будут использоваться для расчета динамической нагрузки и общей нагрузки.

4. Щелкните Рассчитать .

Примечание: В диалоговом окне «Таблица нагрузок на опоры » в правом верхнем углу отображается легенда, помогающая определить местоположение опоры в пролете.

Таблица нагрузок на ноги отображает все стойки в соответствии со спецификациями чертежа.

Если участки являются общими, в диалоговом окне Таблица нагрузок на ноги они отображаются в таблице только один раз. Нога с наибольшей нагрузкой выделена в таблице.

Для получения информации о добавлении информации о нагрузке на ноги в чертеж см. Копирование таблицы нагрузок на ноги в чертеж ниже.

Для получения подробной информации о расчетах см. Детали расчета нагрузок на ноги выше .

Информацию о подвешенных нагрузках на опоры см. В разделе «О подвешенных нагрузках » выше.

Копирование таблицы нагрузок на ноги в чертеж

Вы можете добавить копию таблицы нагрузок на ноги на любую страницу чертежа.

Чтобы скопировать таблицу нагрузок на ноги в чертеж:

1. Щелкните вкладку Подмости и затем щелкните Нагрузки на ноги .

Появится диалоговое окно Таблица нагрузок на ноги .

2. Щелкните текстовое поле Unit Live Load и введите соответствующую нагрузку.

3. Щелкните текстовое поле Количество используемых уровней колод и введите соответствующее количество уровней.

Оба значения будут использоваться для расчета динамической нагрузки и общей нагрузки.

4. .Щелкните Рассчитать .

Примечание: В диалоговом окне «Таблица нагрузок на опоры » в правом верхнем углу отображается легенда, помогающая определить местоположение опоры в пролете.

В таблице отображаются все ножки в соответствии со спецификациями чертежа.

5. Щелкните Копировать в буфер обмена .

6. Щелкните Закрыть , чтобы вернуться на страницу чертежа.

Таблицу нагрузок на ноги можно вставить на любую страницу чертежа с помощью стандартных команд Windows.

7. Щелкните правой кнопкой мыши страницу чертежа и выберите Вставить в появившемся меню.

Изображение таблицы нагрузок на ноги появляется на странице чертежа. Вы можете изменить размер этого изображения и переместить его в желаемое место на странице.

ПРЕДУПРЕЖДЕНИЕ: Если вы внесете изменения в чертеж после добавления таблицы нагрузок на ноги, конструктор лесов включит их в расчет нагрузки на ноги.Чтобы включить эти изменения, удалите изображение таблицы «Нагрузки на ноги» и скопируйте обновленную таблицу «Нагрузки на ноги» в чертеж.

.