Урок 27. углы. измерение углов — Математика — 5 класс
Математика
5 класс
Урок № 27
Углы. Измерение углов
Перечень рассматриваемых вопросов:
— понятие «угол», «величина угла»;
— виды углов;
— построение углов;
— измерение величины угла.
Тезаурус
Угол – геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки, которая называется вершиной угла.
Градус – единица измерения углов, составляющая часть развёрнутого угла.
Градусная мера угла – число, которое показывает, сколько единиц измерения (градусов) содержится между сторонами этого угла.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О.Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия», – сказал в своё время французский архитектор Ле Корбюзье, и трудно с ним не согласиться. Геометрические фигуры постоянно встречаются в творениях природы и человека.
Сегодня мы рассмотрим ещё одну геометрическую фигуру – угол, разберём его виды и опишем процесс построения и измерения углов.
Для начала определим, что называют углом.
Углом называют геометрическую фигуру, образованную двумя лучами, выходящими из одной точки.
Построим угол. Для этого отметим на плоскости точку О и проведём два луча – ОК и ОМ. Получим геометрическую фигуру, образованную точкой О и двумя лучами, исходящими из этой точки.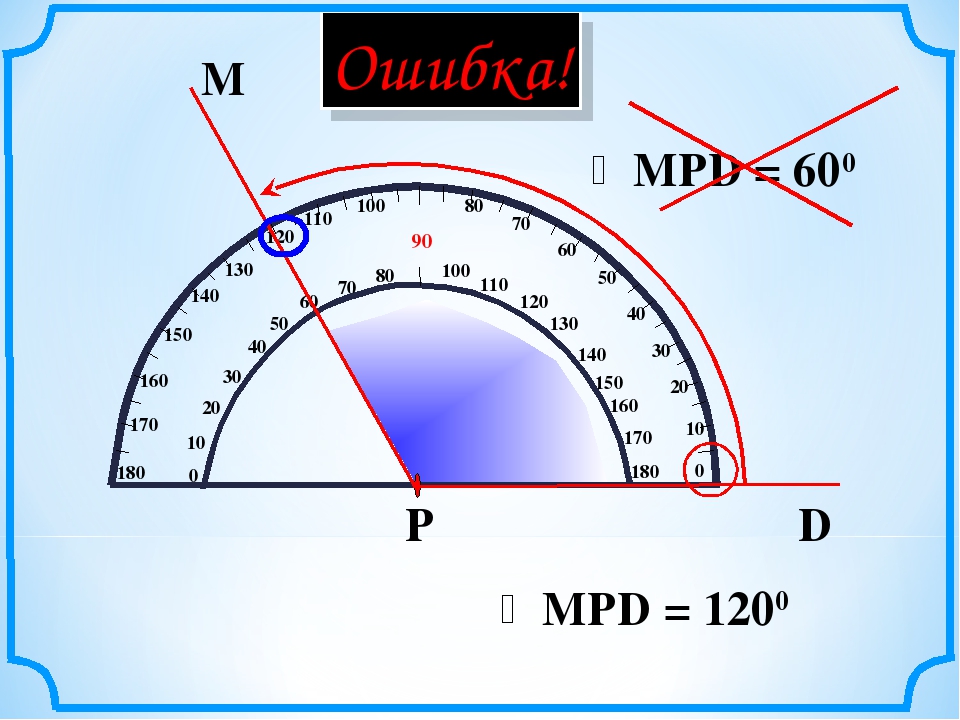 Такую геометрическую фигуру и называют углом.
Такую геометрическую фигуру и называют углом.
Лучи ОК и ОМ называют сторонами угла, точку О – общее начало этих лучей – называют вершиной угла.
Обозначается угол чаще всего тремя буквами. Например, ∠КОМ или ∠МОК. В середине пишется буква, которой обозначена вершина угла. Также угол можно обозначать и одной буквой, поставленной у вершины угла. Например, ∠О.
Начертим два луча, исходящих из точки О и принадлежащих одной прямой.
Лучи ОС и OК вместе с точкой О дополняют друг друга до прямой – это дополнительные лучи. Угол называют развёрнутым, если его стороны являются дополнительными лучами.
Угол СОК – развёрнутый.
Построим развёрнутый угол АОВ и полуокружность с центром в точке О. Полуокружность разделим на 180 равных частей. Если построим углы с вершиной в точке О, стороны которых проходят через точки деления полуокружности, то таких углов будет 180. Один такой угол будет составлять часть развёрнутого угла.
рисунок
Меру угла, составляющего часть развёрнутого угла, принимают за единицу измерения углов и называют градусом. Обозначают: 1º.
Градусной мерой угла называют число, которое показывает, сколько единиц измерения (градусов) содержится между сторонами этого угла.
Например, градусная мера угла КOВ равна 25 градусам, так как в нём единица измерения градус содержится двадцать пять раз. Записывают: ∠КОВ = 25º.
рисунок
Стоит отметить, что для более точного измерения угла используют доли градуса:
– минуты, которые обозначают одной чёрточкой сверху над цифрой справа,
– секунды, которые обозначаются двумя чёрточками над цифрой справа.
В одном градусе содержится 60 минут, а в одной минуте – 60 секунд.
Например, если угол А равен 10 градусам 5 минутам, записывают: ∠А = 10º5′.
Градусная мера развёрнутого угла равна 180º.
Для измерения углов в градусах пользуются прибором, который называется транспортиром. На транспортире имеется шкала – полуокружность, разделённая на 180 равных частей. На линейке транспортира чёрточкой отмечен центр полуокружности транспортира.
На транспортире имеется шкала – полуокружность, разделённая на 180 равных частей. На линейке транспортира чёрточкой отмечен центр полуокружности транспортира.
Чтобы найти градусную меру угла, например, угла АВС, нужно совместить центр транспортира с вершиной угла, в данном случае точкой В; расположить линейку транспортира так, чтобы одна из сторон угла прошла через начало отсчёта шкалы транспортира – ноль градусов(в данном случае сторона АВ), и найти на шкале транспортира деление, через которое проходит другая сторона угла – в данном случае сторона ВС.
Это деление шкалы покажет градусную меру угла. В нашем случае – это 120º.
Транспортир применяется также для построения угла, мера которого известна. Построим, например, угол KNM, равный 60º. Для этого:
— проведём луч NM;
— совместим центр транспортира с точкой N;
— расположим линейку транспортира так, чтобы луч NM прошёл через начало отсчёта шкалы транспортира;
— найдём на шкале транспортира деление, соответствующее шестидесяти градусам, и отметим напротив него точку К;
— проведём луч NK. Мы построили угол KNM, равный 60º.
Ответить на вопрос, равны ли углы, и, если не равны, то какой из них больше или меньше, можно, сравнивая их градусные меры. Углы с равными градусными мерами равны. Из двух углов больше тот, который имеет большую градусную меру; а меньше тот, который имеет меньшую градусную меру.
Углы можно сравнить также наложением. Если при этом они совпадают, то равны.
Помимо развёрнутого, углы можно разделить на следующие виды: прямой, острый и тупой.
Угол называют прямым, если его градусная мера равна 90º.
Острым – если его градусная мера меньше 90º.
Тупым – если его градусная мера больше 90ºи меньше 180º.
Рассмотрим ещё два вида углов, которые встречаются в геометрических задачах: это вертикальные углы, то есть пара углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. Например, угол один и два.
Например, угол один и два.
И смежные углы – это два угла, у которых одна сторона общая, а две другие являются дополнительными полупрямыми.
Например, угол САВ и угол САD.
Вместе смежные углы составляют развёрнутый угол. Следовательно, сумма величин смежных углов составляет 180º.
Итак, сегодня мы познакомились с разными видами углов и научились строить их с помощью транспортира.
Для определения величины углов используется прибор, который называют транспортир. Но существуют и более высокоточные приборы.
Так, гониометр использовался для определения положения судна в море или океане.
Теодолит – прибор для измерения горизонтальных и вертикальных углов при геодезических работах, в строительстве и т. п.
Секстант применялся для измерения высоты Солнца над горизонтом с целью определения географических координат той местности, в которой производится измерение, и на судах.
Посох Якова, служащий для измерения углов, – один из первых инструментов для астрономических наблюдений.
Измерение углов. Транспортир | Математика
Измерить угол — значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.
Обычно за единицу измерения углов принимают градус. Градус — это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °
, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).
Измерение углов транспортиром
Для измерения углов используют специальный прибор — транспортир:
У транспортира две шкалы — внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:
Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов
и пишут: ∠BOC = 60°, ∠MON = 120°.
Для более точного измерения углов используют доли градуса: минуты и секунды. Минута — это угол, равный
части градуса. Секунда — это угол, равный части минуты. Минуты обозначают знаком ‘
, a секунды — знаком »
. Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:
50°34‘19».
Свойства измерения углов
Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.
Рассмотрим угол AOB:
Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.
Развёрнутый угол равен 180°.
Любой угол имеет определённую величину, большую нуля.
Как определить величину угла в градусах в документе photoshop
Каждый наверняка знает, что в приложениях ПК для вызова каждой функции есть свой определенный путь. И вовсе не нужно нервно перебирать все пункты меню в поисках нужного инструмента.
Нужно лишь соблюдать заложенную в программе последовательность действий или нажать нужную комбинацию клавиш. Но зачастую пользователи забывают путь к открытию той или иной функции в программе.
А возможно, даже и не знают его вовсе.
В программе Photoshop принцип действий заключен в визуализации. Для того чтобы вызвать ту или иную функцию, нужно перейти в раздел меню, отвечающий за эту область. Однако порой случается ситуация, что поиск не приносит результатов и пользователь начинает нервничать. Если помощи ждать неоткуда, нижеизложенный материал вам непременно поможет.
Для того чтобы вызвать ту или иную функцию, нужно перейти в раздел меню, отвечающий за эту область. Однако порой случается ситуация, что поиск не приносит результатов и пользователь начинает нервничать. Если помощи ждать неоткуда, нижеизложенный материал вам непременно поможет.
В этой статье подробно рассказано о том, как вызвать инструмент «Линейка» в Фотошопе, а также как им правильно пользоваться.
Как включить линейку
Инструмент «Линейки» в англоязычной версии Фотошопа будет звучать как Rulers. Найти этот пункт можно в соответствующем разделе основного меню — «Просмотр».
Либо же можно вызвать линейки сочетанием клавиш CTRL + R. Убрать линейку можно той же комбинацией кнопок.
Помимо умения вызывать или убирать этот инструмент, пользователю необходимо знать еще кое-что. В линейке Фотошопа имеется возможность смены шкалы измерения.
При включении линейки через меню “Просмотр”, по умолчанию откроется стандартная линейка, со шкалой измерения в сантиметрах. Однако есть и другие виды линеек: пункты, дюймы, пиксели и другие. Для смены единиц измерения кликните по линейке правой кнопкой мыши. И далее в появившемся списке выберите нужный вам вариант.
Линейка измерительная, с транспортиром
В основном блоке инструментов программы можно найти всем знакомый инструмент «Пипетка», наверняка каждый без труда его найдет. А в выпадающем меню, при наведении на “Пипетку”, прямо под «Пипетками», располагается нужная нам кнопка для вызова линейки.
В фотошопе линейка применяется для точного вычисления местоположения нужной точки, откуда и производится измерение. После чего измеряется расстояние от этой точки до чего-либо. Может потребоваться измерить длину отрезка, ширину или высоту элемента, углы.
Подведите курсор мыши к точке начала измерения, и потяните по направлению к конечной точке.
Эта манипуляция также вызовет инструмент «Линейки», а данные по измерению можно посмотреть на верхней панели программы.
Щелчком мыши остановите формирование линейки и перейдите в режим измерения.
Крестики на концах полученной линии позволяют скорректировать направление линейки.
Наверху, в параметрах инструмента буквы X и Y отвечают за координаты начальной точки измерения. Символы Ш и В — тут все понятно (ширина и высота). У (не путайте с игреком) — градус угла. L1 – обозначает отрезок между заданными точками.
Для того чтобы вызвать функцию транспортира требуется проделать следующие действия. Зажмите на клавиатуре кнопку ALT и поместите курсор мыши к начальной точке линейки (где крестик). Транспортир позволяет провести угол относительно положения линейки. Второй луч на панели сверху имеет обозначение L2, а угол между L1 и L2 обозначается буквой Y.
Данные в верхнем меню выглядят так:
Также в верхнем меню вы можете найти подсказку “По шкале измерений”. Нужно поставить галочку и это позволит вычислить данные инструмента “Линейка” с помощью шкалы измерений.
Как по линейке выровнять слой
Порой требуется выровнять картинку, для этой задачи применяется линейка. Вызовите инструмент «Линейка» любым удобным способом. После чего в настройках укажите горизонтальный тип выравнивания. Затем потребуется найти и нажать пункт «Выровнять слой».
Выравнивание будет выполнено путем обрезки изображения по размерам указанной рамки.
Либо же можно при этом зажать клавишу ALT. Тогда изображение и все его элементы не изменят своего изначального положения.
Если вы желаете потренироваться и поэкспериментировать с линейкой, то стоит учесть одну вещь. С линейкой невозможно работать на пустом холсте. Необходимо открыть какую-либо картинку, или создать новый документ.
С каждой последующей версией Фотошопа в программу добавляются новые функции. Однако же алгоритм вызова линейки не меняется.
Источник: https://MyPhotoshop.ru/lineyka-guide/
Геометрическая фигура угол: определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной – ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Определение 6
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.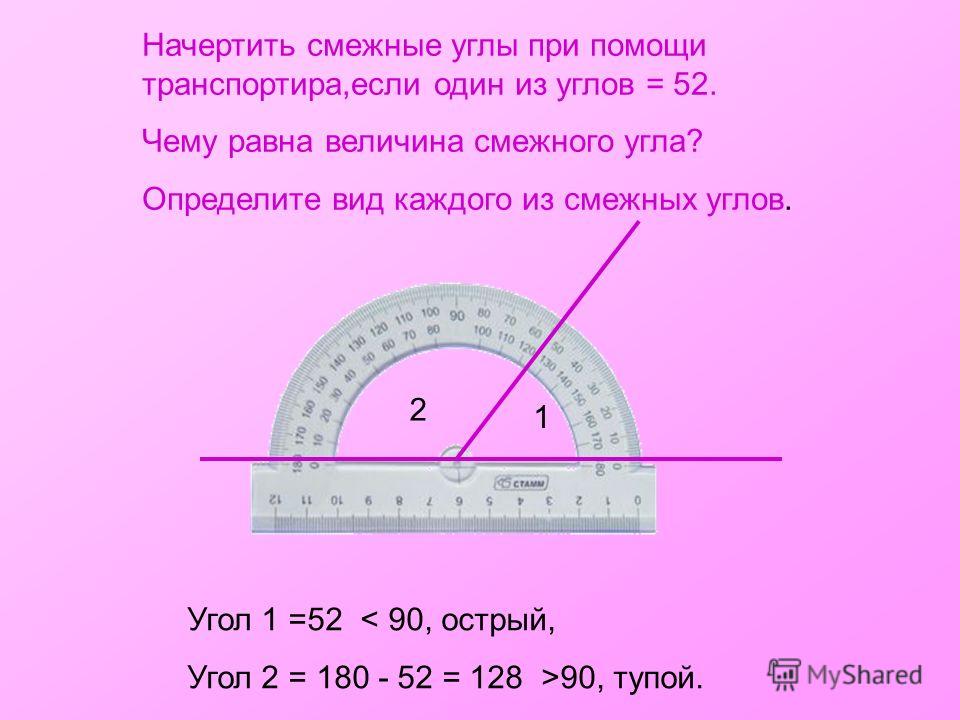
Определение 7
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:
1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .
Определение 11
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение.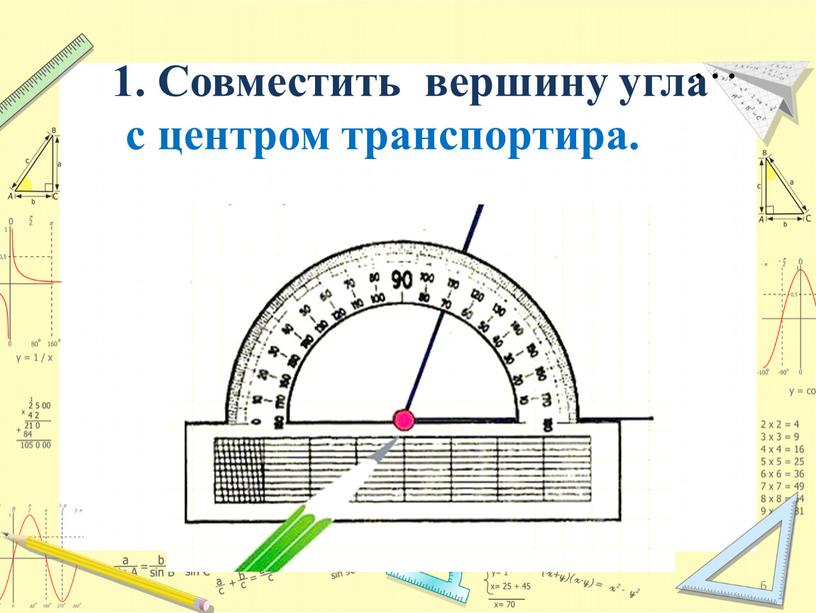 Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны.
Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными.
В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Источник: https://Zaochnik.com/spravochnik/matematika/vektory/geometricheskaja-figura-ugol/
Как в фотошопе повернуть текст на определенный угол? Различные способы
Снова доброго всем времени ! Сегодня продолжим изучать фотошоп, и темой будет редактирование текста. Да-да, именно текста.
Не удивляйтесь, в Photoshop можно не только заниматься рисунками и фотографиями, но и применять к ним текст. Многие наверняка видели в интернете смешные картинки-демотиваторы.
В них как правило всегда есть какой-либо текст, с помощью которого можно очень ёмко и остроумно выражать мысли или эмоции.
Фотошоп — это не текстовый редактор. И конечно, редактировать так, как это делается в специализированном редакторе типа «Word», не получится (да это и ни к чему), но совершить нужные манипуляции с текстом, вроде поворотов, отражений, закручиваний и прочих вполне можно. Photoshop – в первую очередь редактор графический, а потому и изменения текста будут в нем исключительно графические.
Photoshop – в первую очередь редактор графический, а потому и изменения текста будут в нем исключительно графические.
Поворачиваем текст под углом 90 градусов
Начнем с простого примера, а именно с поворота текста под определенным углом. В частности, под углом в 90 градусов. Прежде чем начать это делать, необходимо создать новый слой.
Можно, конечно писать сразу на слое-картинке, но лучше все-таки, делать это на новом слое. В приведенных картинках-примерах я использую только слой с текстом. Нижний слой с названием «Фон» — это та самая картинка.
Итак, создаем слой и пишем на нем то что необходимо.
Фон у нового слоя не сплошной, а в квадратиках. Все нормально, это так отображается прозрачность слоя. Если вы включите фоновый слой, то эти квадратики исчезнут. Что бы написать текст, выбираем на панели инструментов иконку с буквой Т – это и есть «Текст», кликаем по слою и пишем.
Чтобы выбрать цвет текста, жмем перед тем как написать на той же панели инструментов на большой квадрат в самом низу – выбор основного цвета и в открывшемся окне выбираем нужный. Изменить размер шрифта можно на главной панели, где рядом с изображением буквы «Т» показана строка с выпадающем меню, в которой выбирается размер шрифта в пунктах.
Написали текст, нажимаем на стрелку, которая первая на панели инструментов. Тем самым мы закрыли редактор написания текста. Если эту стрелку подвести к тексту и зажать левую кнопку мыши, то текст можно перемещать в любом направлении.
Однако, нам его надо повернуть. Заходим в верхнее меню «Редактирование» и выбираем там «Свободное трансформирование». Вокруг текста появится рамка с квадратиками по углам и по середине.
Если подвести стрелку мыши к одному из углов текста, то увидим, что она приняла форму изогнутой стрелки. Зажав левую кнопку мыши можно вращать текст как угодно.
При этом, на главной панели имеются значки, отображающие поворот и перемещение текста. Поворот показан символом угла, рядом отображаются цифры, показывающие на сколько градусов повернулся текст.
Поворот показан символом угла, рядом отображаются цифры, показывающие на сколько градусов повернулся текст.
Чтобы точно повернуть текст на заданное количество градусов, (в нашем случае 90), достаточно в этом окне ввести необходимую цифру. В результате текст повернется на столько градусов, на сколько задали. Мы подобные приемы уже изучали в одной из статей «Как повернуть картинку в фотошоп«. Как видите и с текстом мы делаем такие же однотипные операции.
Все просто. Одно но, текст повернулся так, что читается он не совсем хорошо. О том как сделать текст развернутым по вертикали и читабельным, будет рассказано дальше.
Как в Photoshop повернуть текст по кругу
Несколько более сложная операция – написание текста по кругу. Сделать это можно двумя способами. Первый, более простой, при помощи деформации. И второй, при помощи контуров. Начнем с простого. Написали текст. Теперь в главном меню находим букву «Т» над дугой. При этом должен быть активирован инструмент «Текст».
Буква «Т» над дугой это и есть кнопка, вызывающая окно деформации текста.
Кстати, может получится такая «фишка», вы нажали на кнопку «Деформации текста», а у вас вместо ожидаемого окна вылезла надпись, что «Невозможно выполнить запрос текстовый слой использует шрифт без данных обвода». Это значит у вас стоит по умолчанию системный шрифт, а он не поддерживает деформирование. В окне выбора шрифта вам надо заменить системный на любой другой.
Итак, открылось окно деформации. Здесь нажимаем на вкладку «стиль» и увидим множество самых различных вариантов деформации текста.
Поскольку нам нужен текст по кругу, выбираем дугой. Ниже видим несколько ползунков, по которым можно изменять конфигурацию текста. Чтобы понять их суть, надо будет немного потренироваться с ними и посмотреть, какие изменения происходят.
Однако деформация не дает написания текста точно по окружности. Здесь придется применить написание текста по контуру.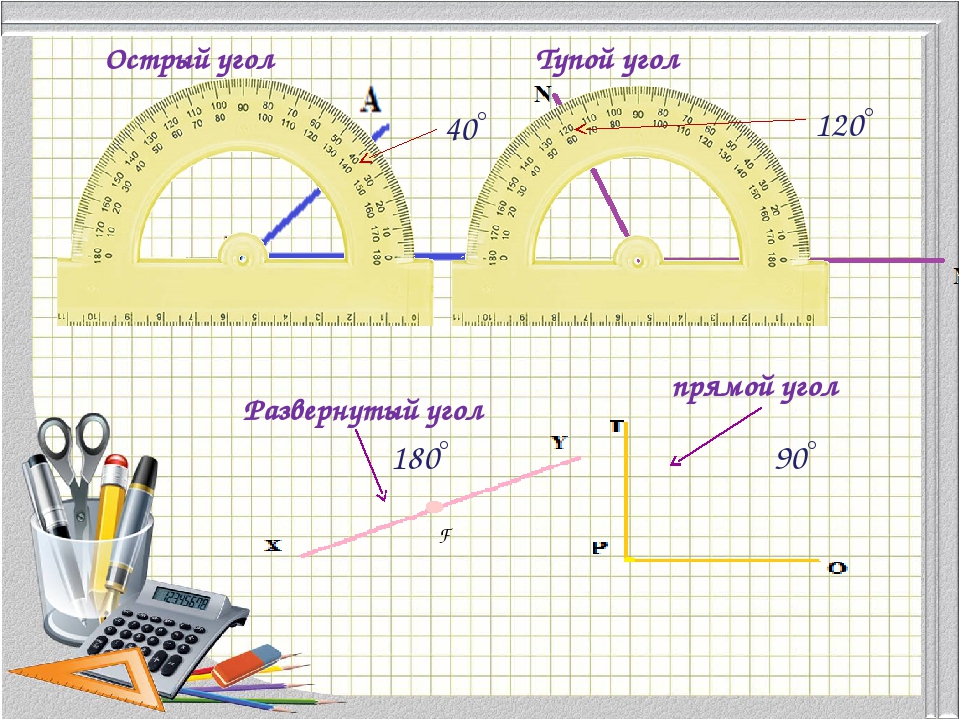 Для этого воспользуемся инструментом «Эллипс». И, самое главное, на главной панели, когда выбрали инструмент эллипс, необходимо заменить его значение «Фигура» на «Контур».
Для этого воспользуемся инструментом «Эллипс». И, самое главное, на главной панели, когда выбрали инструмент эллипс, необходимо заменить его значение «Фигура» на «Контур».
Теперь, удерживая клавишу Shift, рисуем ровный круг-контур. В отличии от круга-фигуры он будет внутри пустой.
Теперь выбираем инструмент текст и подводим его к нарисованному контуру. Когда иконка текста изменится как показано ниже, можно приступать к написанию.
Это изменение текстового курсора означает, что из обычного, он стал привязанным к контуру. При написании текста, вы увидите, что текст идет точно по кругу.
Вот и вся процедура написания. В принципе, ничего сложного.
Как сделать поворот текста вертикально?
Теперь посмотрим, как написать текст вертикально, но не так, как в примере рассмотренном ранее, более читабельно. Здесь, вообще, все очень просто. На панели инструментов нажимаем на уголок инструмента текст и в раскрывшемся меню выбираем «Вертикальный текст». После этого кликаем по рабочему полю и начинаем писать. Текст сразу отображается как надо.
Зеркальный поворот текста в Photoshop
Вся операция по повороту текста зеркально проводится аналогично с поворотом изображений. Пишем текст, далее через верхнее меню заходим в «Редактирование»- «Свободное трансформирование» и там выбираем «Отразить или по вертикали» (или по горизонтали). В результате проделанной операции получится текст зеркально отраженный по вертикали и горизонтали соответственно:
Вот, собственно и все базовые приемы работы с текстом. Теперь Вы знаете, как можно легко можно решать различные творческие задачи. Удачи вам в освоении программы фотошоп.
Источник: https://fast-wolker.ru/kak-v-fotoshope-povernut-tekst.html
Функция ГРАДУСЫ для выполнения геометрических расчетов в Excel
Функция ГРАДУСЫ в Excel используется для преобразования радианной меры угла в соответствующей величину, выраженную в градусах, и возвращает полученное значение.
Пример 1. Для определения количества оборотов вала электродвигателя используется датчик, который определяет и возвращает значение угла в радианах. Спустя минуту работы двигателя было получено значение 2350π. Определить количество оборотов за 1 минуту.
Исходные данные:
- Для расчета используем формулу:
- =ГРАДУСЫ(2350*ПИ())/360
- Описание составляющих:
- 2350*ПИ() – функция, преобразует радианную меру угла 2350*ПИ() и возвращающая значение, выраженное в градусах.
- 360 – полное количество градусов в окружности.
В результате получим:
То есть, двигатель сделал 1175 оборотов за 1 минуту.
Пример 2. Автомобиль движется по круговой трассе. Определить, на какой угол он отклонится относительно начальной точки пути через 17 минут, если за 10 минут он проехал расстояние, равное радиусу окружности трассы.
Исходные данные:
Для определения угловой скорости разделим количество радиан на время пути. Известно, что за 10 минут был пройден путь, равный радиусу окружности. Из этого следует, что автомобиль отклонился на 1 радиан от начальной точки пути. Искомая угловая скорость:
- 1 – количество радиан;
- 10 – время пути в минутах.
Результат:
То есть, 1 рад/мин. Для нахождения искомого угла используем формулу:
Описание:
- B3 – скорость в рад/мин;
- 17 – время пути в минутах.
Результат вычислений:
То есть, автомобиль отклонится примерно на 97°.
Как перевести радианы в градусы в Excel
Пример 3. Определить угол (в градусах), который проходит минутная стрелка механических часов, если часовая успела отклониться от момента отсчета на 0,05236 радиана?
Исходные данные:
Описание величин:
- B3 – количество делений для минутной стрелки.
- B3/B2 – количество делений, которые проходит часовая стрелка за полный оборот минутной.
 То есть, выражение B3/(B3/B2) определяет, во сколько раз скорость минутной стрелки превышает скорость часовой стрелки.
То есть, выражение B3/(B3/B2) определяет, во сколько раз скорость минутной стрелки превышает скорость часовой стрелки. - B4 – отклонение часовой стрелки в радианах.
Полученный результат:
Минутная стрелка отклонится на 36°.
Особенности использования функции ГРАДУСЫ в Excel
Функция ГРАДУСЫ имеет следующую синтаксическую запись:
=ГРАДУСЫ(угол)
Единственным аргументом данной функции является угол (обязательный для заполнения). Он характеризует величину угла, выраженную в радианах.
Примечания 1:
- Excel выполняет автоматическое преобразование данных к требуемому типу в тех случаях, где это возможно. Например, запись типа =ГРАДУСЫ(ИСТИНА) соответствует записи =ГРАДУСЫ(1) и вернет значение 57,29577951, то есть количество градусов в 1 радиане.
- Рассматриваемая функция может принимать в качестве аргумента числа из диапазона отрицательных значений. Например, если в аргументе функции указано значение (-1,5), тогда результат равен -85,94366927.
- Функция вернет код ошибки #ЗНАЧ!, если в качестве аргумента была передана текстовая строка, которая не может быть преобразована в числовой тип данных.
Примечания 2:
- В геометрии углом считается фигура, образованная двумя лучами, которые проведены из одной точки (точки их пересечения), при этом данные лучи называются сторонами угла, а точка – его вершиной.
- Градусы и радианы являются двумя количественными характеристиками размера угла.
- 1 градус соответствует 1/180 развернутого угла, то есть угла, стороны которого лежат на одной прямой.
- Если точка пересечения сторон угла (вершина) является центром окружности, а его стороны – радиусы данной окружности, то радиан – центральный угол, радиусы и длина образованной данным углом дуги являются равными величинами (AO=BO=AmB):
- Между градусной и радианной мерами угла установлена следующая взаимосвязь: град=2π*рад/360°, где рад – количество радиан, а град – рассчитываемое количество градусов.

Источник: https://exceltable.com/funkcii-excel/primer-funkcii-gradusy
Уклон и Конусность
Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки.
Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали.
Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона.
Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах
Конусность.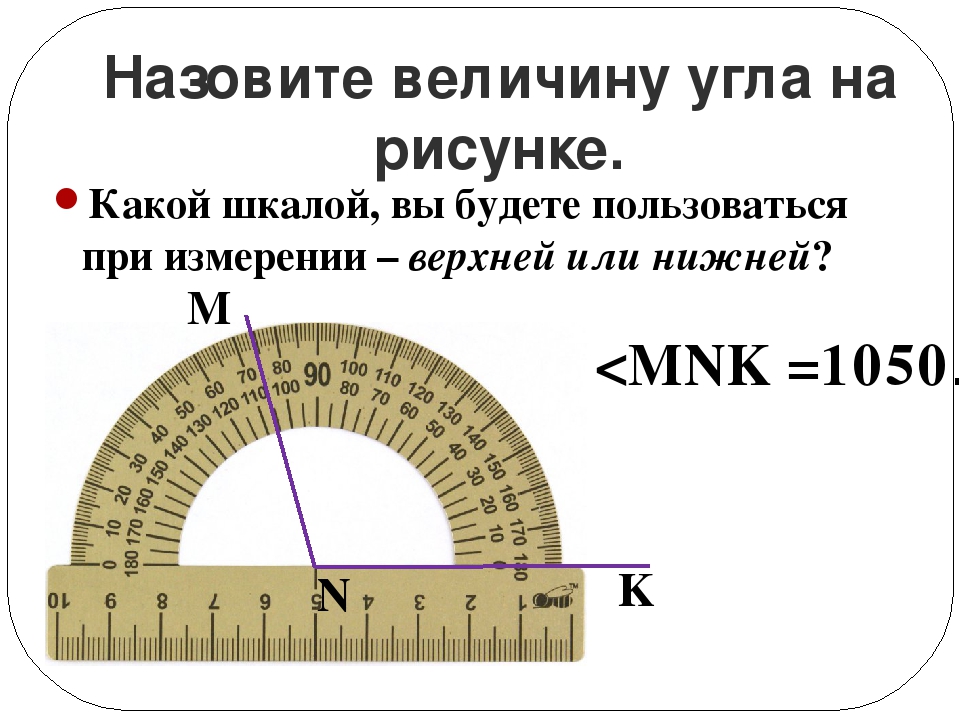 Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Обозначение конусности на чертежах.
Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
Источник: https://chertimvam.ru/uklon-konusnost/
Инструмент линейка в фотошоп: основные функции
Приветствую покорителей фотошопа!
Сегодня речь пойдет о таком инструменте в фотошоп как линейка. Инструмент линейка позволяет не только измерить расстояние между точками, но также повернуть изображение, расположив его строго горизонтально.
Где находится линейка?
Инструмент находиться там же, где и «Пипетка» Для быстрого доступа можно использовать комбинацию Shift + I, нажимайте эти клавиши, программа перебором будет включать все инструменты блока «Пипетка», пока не дойдет до «Линейки».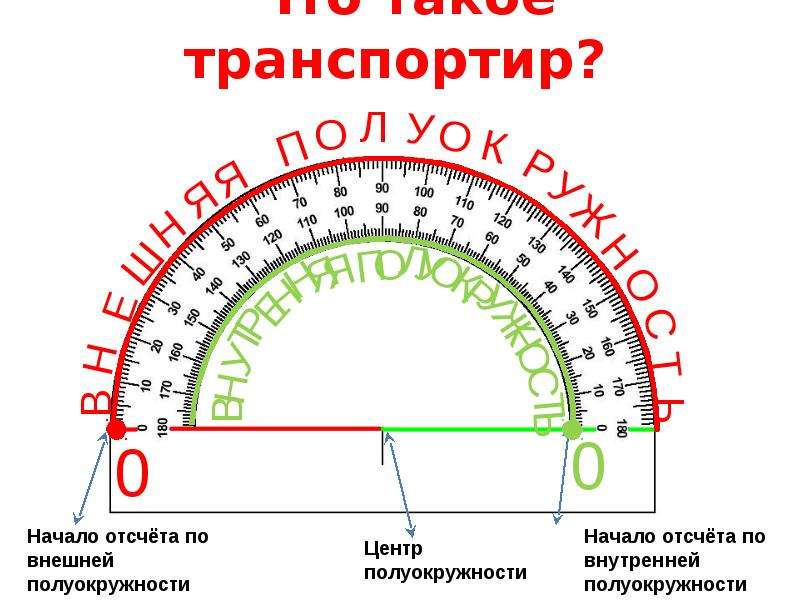
На экране появится черная стрелочка с маленькой линейкой. Левой кнопкой мыши укажите первую точку, не отпуская мышку, ведите курсор ко второй точке замеряемого отрезка. Фотошоп нарисует отрезок.
- Чтобы сделать абсолютно ровную линию, зажмите клавишу Shift, теперь можно отложить отрезок ровно по горизонтали, по вертикали, а также под углом в 45 градусов в любом из направлений.
- После того, как вторая точка отрезка указана, программа покажет все параметры на дополнительной панели, которая находиться над рабочей областью.
Функционал линейки
Здесь информация представлена в виде блоков. Первый показывает координаты первой точки отрезка относительно осей X и Y.
Второй блок показывает проекцию нарисованной линии на ось X и Y. Это не длина отрезка.
Например, если на изображении нарисован прямоугольник, и инструментом «Линейка» указать диагональ этого прямоугольника, то второй блок покажет расстояние сторон прямоугольника. Это и есть прямая проекция отрезка на оси X и Y.
Следующий блок отображает угол наклона отрезка. И только дальше можно увидеть непосредственную длину линии, она указывается в параметре «L1».
Параметр «L2» указывает угол между двумя линиями, нарисованными с помощью инструмента «Линейка». После того, как указан один отрезок, зажмите клавишу Alt, подведите курсор к любому концу отрезка, курсор поменяет свой вид, теперь нарисуйте еще один отрезок, обязательно начиная его с любого из концов первой линии.
Нарисованную линию отрезка вы всегда можете перемещать или изменять. Наведите курсор на тело линии, зажмите левую кнопку мышки и двигайте отрезок в любое место.
Если отрезок надо уменьшить или удлинить, нажмите левую кнопку мышки, размещая курсор на одном из концов отрезка, станет доступна возможность изменить отрезок и указать его новую конечную точку.
Дальше отображается функция «По шкале измерений» (Use Measurement Scale).
Установите флажок, если хотите, чтобы параметры инструмента «Линейка» выводились в тех же единицах, что и разбивочная линейка вокруг всего изображения. Чтобы изменить отображение разбивочной линейки, подведите к ней курсор, нажмите правую кнопку мышки и из списка выберете удобную шкалу линейки.
Чтобы повернуть изображение так, чтобы любая линия на рисунке была строго горизонтальной, используйте следующий блок, который называется «Выровнять слой» (Straighten Layer).
Нарисуйте отрезок с помощью инструмента «Линейка» вдоль любого элемента и нажмите функцию этого блока. Изображение повернется так, что нарисованный отрезок будет расположен строго горизонтально, под каким бы углом он не был раньше.
Последний блок позволяет удалить нарисованный отрезок. Предыдущая линия удаляется автоматически, если вы начинаете рисовать новый отрезок. Если нарисованный отрезок не удалить, при печати он не отображается – это вспомогательный, а не графический элемент.
На этом все. Благодарю за внимание!
Источник: https://CompforLife.ru/fotoshop/instrument-linejka-v-fotoshop.html
Измерение углов
- Измерение углов транспортиром
- Свойства измерения углов
Измерить угол – значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.
Обычно за единицу измерения углов принимают градус. Градус – это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).
Измерение углов транспортиром
Для измерения углов используют специальный прибор – транспортир:
У транспортира две шкалы – внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.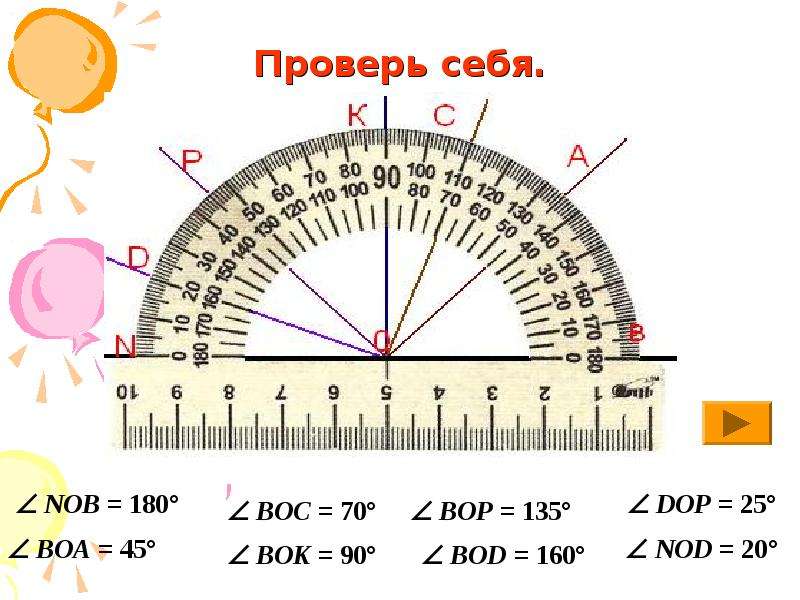
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:
Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов и пишут: ∠BOC = 60°, ∠MON = 120°.
Для более точного измерения углов используют доли градуса: минуты и секунды. Минута – это угол, равный части градуса. Секунда – это угол, равный части минуты. Минуты обозначают знаком ‘, a секунды – знаком ». Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:
- 50°34’19»
- Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.
- Рассмотрим угол AOB:
Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.
Развёрнутый угол равен 180°.
Любой угол имеет определённую величину, большую нуля.
Источник: https://naobumium.info/planimetriya/ugol5.php
Транспортир онлайн, инструмент для измерения углов
Это прозрачный онлайн-транспортир, также помогает измерять углы на изображении, вы можете легко измерить угол любого объекта вокруг вас, сфотографировать и загрузить его, затем перетащить среднюю точку транспортира к вершине угла.
Как пользоваться этим онлайн-транспортиром?
- Вы можете измерить угол любого реального объекта прямо на вашем экране
- Если вы хотите переместить транспортир, перетащите его середину.
- Нажмите на край снаружи транспортира, чтобы добавить к нему метку
- Размещение двух кнопок покажет градусы этого угла
- Двойной щелчок на кнопке удалит ее
Каждый раз, когда я хочу измерить угол, я всегда не могу найти транспортир. К счастью, вот онлайн-транспортир, который удобен и практичен. Теперь мы можем использовать ноутбуки, компьютеры, планшеты или смартфоны для измерения угла наклона чего угодно, вокруг нас в любое время и в любом месте.
К счастью, вот онлайн-транспортир, который удобен и практичен. Теперь мы можем использовать ноутбуки, компьютеры, планшеты или смартфоны для измерения угла наклона чего угодно, вокруг нас в любое время и в любом месте.
Если вы хотите измерить что-то маленькое, просто поместите его на экран и измерьте прямо; Если вы хотите измерить что-то большее, Вы можете сделать снимок и загрузить его, а затем переместить центральную точку транспортира, чтобы измерить его угол.
Используйте камеру или изображение для измерения угла
Вы можете сфотографировать любой объект, который вы хотели бы измерить, например, автомобиль, дорога, дом, лестница или гора, транспортир прозрачный, после того как вы загрузили изображение, оно будет отображаться в фоновом режиме. затем вы можете убрать транспортир или добавить кнопки, чтобы определить градусы углов, загрузить файл только принять файл изображения в форматах JPG, JPEG, GIF, PNG
На панели управления если цвет фона близок к транспортиру, и это не легко отличить, Вы можете изменить цвет транспортира, чтобы видеть это ясно. Также вы можете переместить его, уменьшить или увеличить размер транспортира, в соответствии с вашими потребностями.
Углы и градусы
- Углы измеряются в градусах. Символом градусов является маленький кружок °
- Полный круг составляет 360 ° (360 градусов)
- Полукруг или прямой угол 180 °
- Четверть круга или прямой угол составляет 90 °
Что вы думаете об этом транспортире?
Источник: https://ginifab.com/feeds/angle_measurement/online_protractor.ru.php
Определение натуральной величины угла
Чтобы определить натуральную величину угла, нужно перевести его в положение, в котором его стороны будут параллельны плоскости проекции. Наиболее рациональный путь решения данной задачи – использовать способ вращения вокруг линии уровня. Более трудоемкими вариантами являются метод замены плоскостей проекций и параллельное перемещение.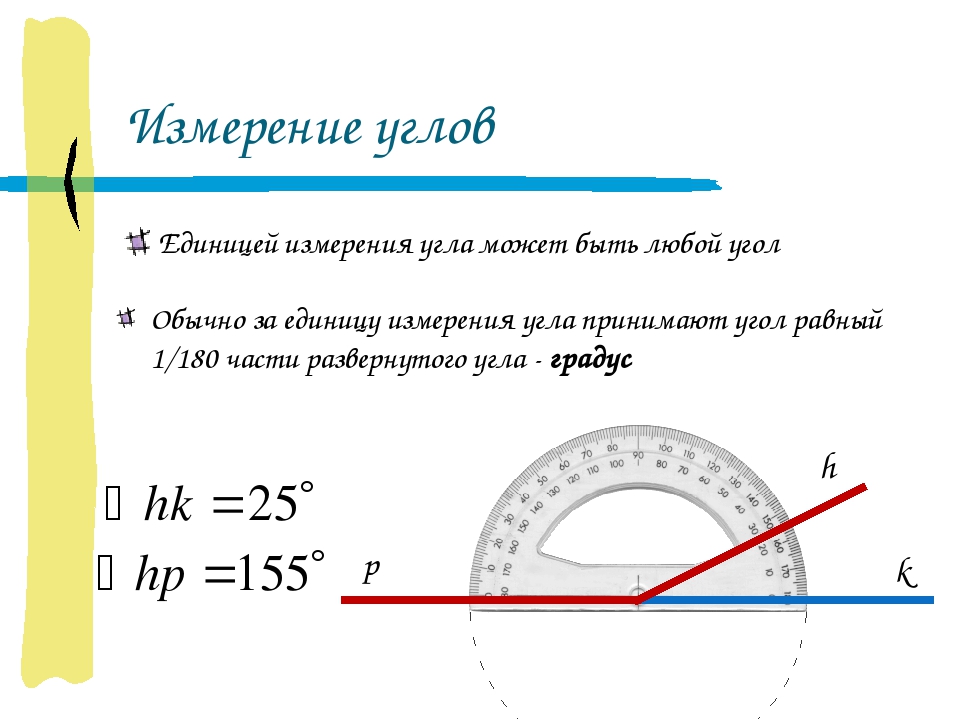
Задача
Приведенный ниже пример иллюстрирует нахождение угла между пересекающимися прямыми m и n способом вращения вокруг фронтали.
Последовательность построений:
- В произвольном месте чертежа проводим фронталь f. Она пересекает прямые m и n в точках 1 и 2. Определяем их недостающие проекции.
- Через точку K» проводим перпендикуляр к f». На пересечении этого перпендикуляра с фронталью находится проекция центра вращения O». По линии связи определяем положение т. O’.
- Находим величину радиуса R поворота точки K. Для этого перпендикулярно O»K» откладываем отрезок K»K0 = yk – yo. Таким образом, R равен O»K0 – гипотенузе прямоугольного треугольника O»K»K0.
- Проводим дугу радиусом R до её пересечения с перпендикуляром O»K» в точке K»1. Соединяем K»1 c точками 1» и 2». Натуральная величина угла между прямыми m и n равна углу ϕ при вершине K»1.
Более подробную информацию о методе вращения вокруг линии уровня, который мы здесь использовали, вы можете найти на следующей странице.
Определение угла между скрещивающимися прямыми
Углом между скрещивающимися прямыми называют плоский угол, стороны которого параллельны данным прямым. На изображении, приведенном ниже, прямые e и d скрещивающиеся и друг с другом не пересекаются. Чтобы найти угол между ними, выполним ряд графических построений:
Описание решения
- На любом свободном месте чертежа отмечаем точку S. Располагаем её произвольно (проекции S» и S’ показаны на рисунке).
- Через точку S проводим прямые a и b так, чтобы они были параллельны e и d. В нашем случае a||e, b||d соответственно.
- Строим горизонталь h, которая будет играть роль оси вращения. Перпендикулярно h’ из точки S’ проводим прямую. Она пересекает h’ в т. O’ – горизонтальной проекции центра вращения.
- Определяем радиус поворота R как гипотенузу треугольника O’S’S0. При этом катет S’S0 равен разности удаления точек S» и O» от горизонтальной плоскости.

- Находим т. S’1 на пересечении дуги радиуса R с прямой S’O’. Соединяем S’1 c точками 1′ и 2′, которые своего положения не меняют. Угол ϕ при вершине S’1 искомый. Задача решена.
Похожие задачи:
Источник: https://ngeometry.ru/kak-opredelit-naturalnuyu-velichinu-ugla.html
«Транспортир. Построение и измерение углов с помощью транспортира. Смежные углы» (8 класс, для школы VIII вида)
На уроке мы вспомним, что такое единицы измерения, узнаем какими единицами можно измерять углы, познакомимся с такой единицей измерения, как градус, научимся измерять углы в градусах и чертить их с помощью транспортира. Также мы узнаем о других единицах измерения углов, которые применяются в различных ситуациях.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок и
Какие-то вещи можно измерить, какие-то нельзя. Например, нельзя измерить дружбу или любовь. А расстояние, вес, температуру вполне можно. Чтобы что-то измерять, нужно всем договориться о единицах измерения.
Метр, дюйм, аршин — это и есть такие договоренности при измерении длины. Эталонный метр хранится во Франции, в Палате мер и весов. Килограмм, фунт, пуд — это договоренности для измерения массы. Эталонный килограмм тоже хранится в Палате мер и весов.
Единицы измерения придуманы для конкретных величин. В секундах не измерить вес, а в аршинах — время.
В геометрии такая же ситуация. Есть сантиметры, для измерения длин отрезков, но они не подходят для измерения углов. Для измерения углов есть свои единицы измерения. На этом уроке мы рассмотрим одну из них, а именно градусы.
Разделим полный угол на 360 равных частей. Для этого удобно использовать окружность. Поделим ее на 360 частей и соединим каждое полученное деление с центром. Получим 360 равных углов (см. Рис. 1).
Рис. 1. Окружность, разделенная на 360 равных углов
Один такой маленький угол назовем углом в 1° (см. Рис. 2).
Рис. 2).
Рис. 2. 1 градус
Не важно, какого размера будет окружность, которую мы делим. Поделим обе окружности на 360 частей, получим равные углы в 1°, хотя стороны одного угла визуально длиннее, чем у другого (см. Рис. 3).
Рис. 3. Углы равны
Стороны углов можно продолжать бесконечно, от этого размер угла не меняется (см. Рис. 4).
Рис. 4. Более явный пример равенства углов
Величина любого угла — это сколько раз в него умещается угол в 1°.
Вот мы видим угол 13° (см. Рис. 5).
Рис. 5. Угол 13°
Понятно, что полный угол
состоит из 360 таких углов. То есть он равен 360° (см. Рис. 6).
Рис. 6. Полный угол
Развернутый угол
— это половина полного угла. Он равен (см. Рис. 7).
Рис. 7. Развернутый угол
Прямой угол
является половиной развернутого и равен 90° (см. Рис. 8).
Рис. 8. Прямой угол
Эталон градуса нет нужды где-то хранить. Если нужно, то всегда можно полный угол разделить на 360 частей, или развернутый — на 180, или прямой — на 90.
Линейка нужна для того, чтобы измерить имеющийся отрезок или начертить отрезок нужной длины. Чтобы измерить угол или начертить угол нужной величины, мы тоже используем линейку, только не прямую, а круглую. Она называется транспортиром (см. Рис. 9).
Рис. 9. Транспортир
Единицы измерения на ней — градусы. Шкала начинается с нуля и заканчивается 180°.То есть максимальный угол, который мы можем измерить или начертить, — это 180°, развернутый.
Транспортиры могут быть разных размеров, но это не влияет на то, какого размера углы ими измеряют. Для более крупного транспортира у углов нужно чертить стороны длиннее.
1. Измерим пару углов.
Прямая часть транспортира совмещается с одной стороной угла, центр транспортира с вершиной угла. Смотрим, где оказалась вторая сторона угла, — 54° (см. Рис. 10, 11).
Рис. 10. Измерение угла
Проделаем то же самое со вторым углом, 137°.
Рис. 11. Измерение угла
Если сторона угла не достает до шкалы, то ее нужно сначала продлить.
2. Начертим углы 29°, 81° и 140°.
Сначала чертим одну сторону угла по линейке (см. Рис. 12).
Рис. 12. Построение одной стороны угла
Отмечаем вершину. Совмещаем с транспортиром. Отмечаем точкой нужное значение угла — 29° (см. Рис. 13).
Рис. 13. Использование транспортира для построения углов
Убираем транспортир. Соединяем полученную точку с вершиной (см. Рис. 14).
Рис. 14. Угол 29°
Точно так же строим два других угла (см. Рис. 15).
Рис. 15. Построение углов
Итак, мы с вами обсудили, что для измерения углов люди договорились использовать градусы. Градус
— это полного угла.
Инструментом для измерения и построения углов является транспортир.
Можно не использовать названия углов — полный, развернутый, прямой. Мы можем просто говорить — 360 градусов, 180 или 90 градусов.
На самом деле бывает, когда мы одни величины измеряем единицами, казалось бы, для них не предназначенными, «чужими» единицами.
Можно ли измерить расстояние в минутах? Да, мы часто используем этот способ. «От моего дома до школы 5 минут». Если быть точнее, то «5 минут пешком». Мы здесь используем известную всем величину — скорость пешехода. И величина «5 минут» на самом деле означает «расстояние, которое пешеход проходит за 5 минут». Скорость пешехода — 5 км/ч, 5 минут — это часа, умножим одно на другое. Получаем примерно 400 метров. Не очень точно, зато удобно.
Точно по такому же принципу устроена другая единица измерения расстояния — световой год. Световой год — расстояние, которое проходит свет за 1 год. С помощью этой единицы меряют расстояния между звездами.
Очень распространенный пример использования «чужой» единицы измерения — это измерять вес в килограммах. На самом деле килограмм — единица измерения массы, а вес — это другая физическая величина. Если хотите подробнее узнать, в чем разница между массой и весом, и почему измерять вес в килограммах не верно, то наберите в поисковой системе «масса и вес» и получите множество пояснений по этому поводу.
Атмосферное давление мы до сих пор измеряем в миллиметрах (миллиметрах ртутного столба).
Хотя для угла есть свои «родные» единицы измерения — градусы, которые мы и проходим на этом уроке, все-таки его можно измерять и с помощью линейных величин, например сантиметров. Если нужно измерить угол , то можно достроить его до треугольника, так чтобы один угол был прямым, и разделить длину одной стороны на другую.
Получим величину угла , которая называется тангенсом.
Если увеличить треугольник, то ничего не изменится (см. Рис. 16).
Рис. 16. Тангенс
Ведь во сколько раз увеличилась одна сторона, во столько и вторая.
То есть величины часто можно измерять «чужими» единицами, но это чуть сложнее, там нужны некоторые дополнительные договоренности.
Существуют и другие единицы измерения углов.
1.
Минуты и секунды.
Как и метр можно делить на дециметры, сантиметры, миллиметры для более точных измерений, так и градусы делятся на более мелкие единицы измерения.
Если угол в 1° разделить на 60 равных частей, то величина полученного угла называется минута, 1′.
Если минуту поделить на 60 частей, то полученная величина называется секундой. Секунда — уже очень маленькая величина, но ее тоже можно делить дальше.
Почему вообще стали делить на 360 частей полный угол, ведь это не очень удобно? В древнем Вавилоне была шестидесятеричная система (у нас десятеричная). Им было удобно делить на 60.
2.
Грады.
Чтобы сделать измерение углов ближе к нашей десятичной системе счисления, были предложены грады. Для этого прямой угол делится на 100 частей. Полученная величина называется град. Полный угол составляет тогда 400 градов. Система не прижилась, и сейчас ее не используют.
3.
Радиан.
Если взять два радиуса окружности так, чтобы кусочек окружности между ними тоже был равен радиусу, то угол между радиусами мы и примем за новую единицу измерения. Он называется 1 рад (радиан). Эта мера используется наравне с градусной. У нее есть свои преимущества и свои недостатки по сравнению с градусами (см. Рис. 17).
Рис. 17. Радианы
Например, теперь полный угол (вся окружность) состоит не из целого числа единичных углов. Полный угол состоит из 6 с лишним единичных углов. Не очень удобно, зато теперь длина дуги (части окружности) и угол хорошо связаны. Если взять окружность радиуса 1 см, то величина угла совпадает с длиной дуги. Угол 1 рад — дуга 1 см, угол 2 рад — длина дуги 2 см.
Список литературы
- Зубарева И.И., Мордкович А.Г. Математика. 5 класс. — М.: Мнемозина, 2013.
- Виленкин Н.Я. и др. Математика. 5 кл. — М.: Мнемозина, 2013.
- Ерина Т.М. Математика 5кл. Раб. тетрадь к уч. Виленкина, 2013. — М.: Мнемозина, 2013.
- Shkolo.ru ().
- Cleverstudents.ru ().
- Festival.1september.ru ().
Домашнее задание
- Зубарева И.И., Мордкович А.Г. Математика. 5 класс. — М.: Мнемозина, 2013. Стр. 144 № 522.
- Начертите углы: 23°, 167°, 84°.
- Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 5 класса (5-е изд.) — 2010. Стр. 163 № 3.
Как измерить угол?
При решении задач в геометрии мы постоянно сталкиваемся с разными фигурами — плоскими и объемными. Большинство геометрических фигур состоит из сторон и углов. Исключение составляют круг, эллипс, шар. Измерение углов — важная часть решения, иногда только правильное измерение и помогает решить задание и найти верный ответ.
Как же правильно измерить угол?
Транспортир — это специальный прибор, в чем то похожий на линейку, который имеет дугу с нанесенной на нее шкалой. Цифры на этой шкале означают градусы. А в градусах, как известно, и измеряют углы.
Как измерить угол транспортиром
Достаточно приложить центр транспортира к точке — вершине угла. Центр транспортира — это маленькая точка под дугой на прямой линии. В нем часто делают небольшое отверстие, чтобы было удобно накладывать его на вершину угла.
Как измерить угол без транспортира
В некоторых частных случаях угол можно отсчитать по клеткам в тетради. Например, угол 90° рисуется как 2 перпендикулярные линии, выходящие из одной точки. Они совпадают с клетками тетради и по горизонтали, и по вертикали. Если же одна сторона угла совпадает с клетками горизонтально, а другая пересекает каждую клеточку ровно по диагонали, то этот угол будет равен 45°.
Есть также способ измерения угла при помощи часов. Если вы вдруг забыли транспортир, а на руке у вас часы со стрелками, то попробуйте приложить центр часов к вершине угла, одну сторону совместить с цифрой 6, а вторую продлить пунктиром. Одна минута будет равна 6 градусам.
Способ, конечно, не очень удобный, но иногда спасает.
Еще в школе каждый человек сталкивался с такой вещью, как транспортир. Но, к сожалению, далеко не каждый, как в школьное время, так и уже в старшем возрасте, знает, как правильно им пользоваться. Данная инструкция научит каждого правильно пользоваться этим предметом.
Начнем, пожалуй, с того, что же такое транспортир. Транспортир – это инструмент для измерения градусного значения углов. Чаще всего такой инструмент имеет полукруглую форму. Но есть и исключения, а именно транспортиры, которые имеют полностью круглую форму (360 градусов).
Как правильно пользоваться транспортиром
- Для начала необходимо понять, что представляет из себя данный инструмент. Он являет собой полукруглый предмет (как уже было сказано выше, может быть и круглый) с небольшим отверстием в середине, которое называется точкой отсчета. Именно последнее (точку отсчета) нужно совместить с вершиной треугольника.
- Дальше для измерения необходимого угла, необходимо основание транспортира разместить параллельно стороне угла или катету треугольника. Для этого нужно выбрать сторону треугольника (она будет базовой, именно с этой стороной нужно совместить основание транспортира). Не стоит путать базовую линию угла и основание транспортира (это совершенно разные вещи).
- Как только вы совместили точку отсчета с вершиной угла, а основание транспортира с катетом, можно смело измерить угол. Тогда второй катет треугольника будет указывать на шкалу с цифрами на полуокружности транспортира. Главное – это не запутаться с цифрами, ведь сделав это, вы допустите ошибку в измерении необходимого угла.
- Стоит понимать, что чем больше (тупее) угол, тем больше его градусное значение. Угол максимально может составить 180 градусов.
- Самые маленькие (острые) углы могут составлять только меньше 90 градусов, все, которые будут больше этого значения уже считаются большими (тупыми).
Как правильно измерить градусное значение угла транспортиром
Для этого необходимо сделать следующие действия:
- Центральную точку (точку отсчета) необходимо совместить с вершиной угла, который необходимо измерить. Транспортир необходимо зафиксировать на данном месте с помощью ручки, карандаша или любого другого предмета. После этого его необходимо повернуть таким образом, чтобы одна из сторон угла совпала с основанием транспортира (полуокружность с градусной шкалой должна смотреть вверх).
- Теперь необходимо посмотреть, на какое число на полуокружности указывает вторая сторона угла (она должна пересекать полуокружность транспортира). Необходимо посмотреть, через какое число проходит эта линия.
- Если линию продлить невозможно (она все равно не доходит до полуокружности транспортира), следует взять кусочек бумаги или линейку и совместить ее с той стороной, которая не доходит до полуокружности. В таком случае, линейка должна “продлить” вторую сторону угла до пересечения с полуокружностью, на которую указаны градусы.
Как правильно начертить угол при помощи транспортира
- Для начала необходимо начертить линию с помощью транспортира. Такая линия будет базовой. Именно по ней вы будете ориентироваться, чтобы начертить вторую. Для лучшего удобства ее нужно расположить горизонтально.
- На этой линии необходимо отметить точку, которая будет вершиной вашего угла. Такую точку необходимо совместить с точкой отсчета на транспортире.
- Далее необходимо совместить базовую линию угла с основанием транспортира. После этого следует посмотреть на полуокружность транспортира и выбрать необходимое градусное значение. На бумаге следует нарисовать точку рядом с этим значением. К такой точке необходимо будет провести вторую линию из вершины угла.
- После этого можно смело отложить транспортир в сторону.
- Теперь нужно взять в руки линейку и соединить вершину угла и точку, которая уже была нарисована возле нужного вам градусного значения.
Дело сделано! Вы получили угол с необходимым для вас градусным значением. В итоге, хотелось бы сказать, что пользоваться транспортиром достаточно просто, если грамотно использовать все эти советы. Но если же вам удалось немного запутаться с градусными шкалами, стоит помнить, что они абсолютно одинаковы, только идут в противоположных направлениях для удобства использования транспортира.
Измерить угол
— значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.
Обычно за единицу измерения углов принимают градус. Градус
— это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).
Измерение углов транспортиром
Для измерения углов используют специальный прибор — транспортир
:
У транспортира две шкалы — внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:
Говорят: угол BOC
равен 60 градусов, угол MON
равен 120 градусов и пишут: ∠BOC
= 60°, ∠MON
= 120°.
Для более точного измерения углов используют доли градуса: минуты и секунды. Минута
— это угол, равный
части градуса. Секунда
— это угол, равный части минуты. Минуты обозначают знаком »
, a секунды — знаком «»
. Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:
50°34»
19«»
Свойства измерения углов
Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.
Рассмотрим угол AOB
:
Луч OD
делит его на два угла: ∠AOD
и ∠DOB
. Таким образом, ∠AOB
= ∠AOD
+ ∠DOB
.
Развёрнутый угол равен 180°.
Любой угол имеет определённую величину, большую нуля.
Еще в школе каждый человек сталкивался с такой вещью, как транспортир. Но, к сожалению, далеко не каждый, как в школьное время, так и уже в старшем возрасте, знает, как правильно им пользоваться. Данная инструкция научит каждого правильно пользоваться этим предметом.
Начнем, пожалуй, с того, что же такое транспортир. Транспортир – это инструмент для измерения градусного значения углов. Чаще всего такой инструмент имеет полукруглую форму. Но есть и исключения, а именно транспортиры, которые имеют полностью круглую форму (360 градусов).
Как правильно пользоваться транспортиром
- Для начала необходимо понять, что представляет из себя данный инструмент. Он являет собой полукруглый предмет (как уже было сказано выше, может быть и круглый) с небольшим отверстием в середине, которое называется точкой отсчета. Именно последнее (точку отсчета) нужно совместить с вершиной треугольника.
- Дальше для измерения необходимого угла, необходимо основание транспортира разместить параллельно стороне угла или катету треугольника. Для этого нужно выбрать сторону треугольника (она будет базовой, именно с этой стороной нужно совместить основание транспортира). Не стоит путать базовую линию угла и основание транспортира (это совершенно разные вещи).
- Как только вы совместили точку отсчета с вершиной угла, а основание транспортира с катетом, можно смело измерить угол. Тогда второй катет треугольника будет указывать на шкалу с цифрами на полуокружности транспортира. Главное – это не запутаться с цифрами, ведь сделав это, вы допустите ошибку в измерении необходимого угла.
- Стоит понимать, что чем больше (тупее) угол, тем больше его градусное значение. Угол максимально может составить 180 градусов.
- Самые маленькие (острые) углы могут составлять только меньше 90 градусов, все, которые будут больше этого значения уже считаются большими (тупыми).
Как правильно измерить градусное значение угла транспортиром
Для этого необходимо сделать следующие действия:
- Центральную точку (точку отсчета) необходимо совместить с вершиной угла, который необходимо измерить. Транспортир необходимо зафиксировать на данном месте с помощью ручки, карандаша или любого другого предмета. После этого его необходимо повернуть таким образом, чтобы одна из сторон угла совпала с основанием транспортира (полуокружность с градусной шкалой должна смотреть вверх).
- Теперь необходимо посмотреть, на какое число на полуокружности указывает вторая сторона угла (она должна пересекать полуокружность транспортира). Необходимо посмотреть, через какое число проходит эта линия.
- Если линию продлить невозможно (она все равно не доходит до полуокружности транспортира), следует взять кусочек бумаги или линейку и совместить ее с той стороной, которая не доходит до полуокружности. В таком случае, линейка должна “продлить” вторую сторону угла до пересечения с полуокружностью, на которую указаны градусы.
Как правильно начертить угол при помощи транспортира
- Для начала необходимо начертить линию с помощью транспортира. Такая линия будет базовой. Именно по ней вы будете ориентироваться, чтобы начертить вторую. Для лучшего удобства ее нужно расположить горизонтально.
- На этой линии необходимо отметить точку, которая будет вершиной вашего угла. Такую точку необходимо совместить с точкой отсчета на транспортире.
- Далее необходимо совместить базовую линию угла с основанием транспортира. После этого следует посмотреть на полуокружность транспортира и выбрать необходимое градусное значение. На бумаге следует нарисовать точку рядом с этим значением. К такой точке необходимо будет провести вторую линию из вершины угла.
- После этого можно смело отложить транспортир в сторону.
- Теперь нужно взять в руки линейку и соединить вершину угла и точку, которая уже была нарисована возле нужного вам градусного значения.
Дело сделано! Вы получили угол с необходимым для вас градусным значением. В итоге, хотелось бы сказать, что пользоваться транспортиром достаточно просто, если грамотно использовать все эти советы. Но если же вам удалось немного запутаться с градусными шкалами, стоит помнить, что они абсолютно одинаковы, только идут в противоположных направлениях для удобства использования транспортира.
Как правильно пользоваться транспортиром?
У меня два варианта ответа. Один простой и несет в себе информацию того, как именно должно происходить измерение угла. Тут я решила выложить просто видео урок с виртуальным транспортиром, где подробно показан процесс определения угла.
Второй вариант ответа касается того момента, как же умудриться держать транспортир так, чтобы угол измерить правильно? Тут есть много сложностей и неудобств. То транспортир съезжает, то торчит, не прижимается к листу, не видно четко через цветную пластмассу линию угла. Еще хуже, когда через транспортир не видно вообще ничего, даже сами отметки делений градуса углов.
Чтобы правильно измерить угол
, советую любой транспортир, какой бы вы не приобрели, придерживать при измерении тремя (двумя) пальцами. Первая точка снизу справа, вторая точка придерживания транспортира снизу слева, третья сверху по радиусу угла. В таком положении разглядеть угол сложно, так как палец вверху закрывает часть видимости, а без него уползает транспортир.
Поэтому неопытным пользователям лучше брать транспортиры встроенные в линейку,
еще лучше из полностью прозрачной пластмассы.
Такой транспортир удобно придерживается двумя пальцами по центру линейки — все видно и ничего никуда не сползает, не съезжает, плюс отличная видимость через не цветной пластмасс.
Железный транспортир идеально подходит для опытных пользователей (старшекласники), имеет пару недостатков — скользит по бумаге и может погнуться.
Как известно трнспортиры измеряют углы, которые состоят из 2-х лучей. 1-й луч совмещаем с верхом нижней линейки, и 2-й луч при этом покажет величину угла в градусах, которые расположена на верхней полуокружности.
Что такое транспортир?
Транспортиром называют предмет, с помощью которого каждый из нас может не только измерять углы, но и строить их. Внешне он напоминает полукруглую линейку со шкалой и делениями. Внизу, на ровной поверхности, расположена привычная нам прямая линейка для измерения отрезков. В верхней части — полукруг с двойной шкалой для измерений. В каждом из направлений шкала рассредоточена по транспортиру от 0 до 180 градусов.
Правила пользования
В школе объясняют, что такое транспортир, на уроках математики. Именно здесь есть необходимость в измерениях.
Для того чтобы нам узнать, чему равен один градус, нужно окружность поделить на 360 равных частей. Одна из таких частей и будет равна 1 градусу. Величина окружности никак не повлияет на градус! Это легко проверить.
Нарисуем две окружности разного диаметра и поделим каждую на 360 равных частей. Затем наложим меньшую окружность на большую и увидим, что линии совпали.
Измеряем угол
Транспортир помогает построить и измерить угол. Градус — это общепринятая единица, которой пользуются для измерения углов. Встречается несколько разновидностей углов:
- Острый. Таким называют угол до 90 градусов.
- Прямым является угол, равный 90 градусам.
- Тупой угол варьируется в диапазоне от 90 до 180 градусов.
- Развёрнутый угол представляет собой прямую линию или 180 градусов.
- Полный угол выглядит как окружность и составляет 360 градусов.
Нетрудно разобраться, как измерить угол. Для того чтобы узнать, какова величина угла, нам необходимо установить транспортир таким образом, чтобы его центр располагался в вершине угла, а прямая сторона совпала с одной из его сторон. Шкала укажет нам количество градусов данного угла. Вот таким нехитрым способом мы можем узнать, что за угол перед нами.
Для построения угла с заданным градусом следует приложить прямую часть транспортира к линии, а его центр — к началу линии. Впоследствии эта точка будет являться вершиной угла. Затем на шкале отыскиваем заданное число и ставим точку. Теперь транспортир можно снять и соединить отрезком начало линии (вершину угла) с отмеченной точкой.
Школьные канцтовары, произведенные разными компаниями, отличаются по материалу, цвету, размеру. Так вот: тем, у кого транспортир оказался больше длины угла, и не представляется возможным определить его величину, сторону угла необходимо продлить, используя прямую линейку.
Набор школьника
Неспроста учащиеся младшего звена не знакомы с транспортиром. При его применении должна быть заложена некая база знаний. Для полноценной работы с ним на уроке ребята изучают ряд сопутствующих предметов. Прежде чем узнать, что такое транспортир, школьники должны в совершенстве овладеть прямой линейкой, чертить ровные линии, изучить сложение и вычитание, освоить циркуль, знать геометрические фигуры и так далее. Весь этот процесс занимает время, и только окончив начальную школу, ученик может добавить транспортир в свой набор инструментов.
Ученикам сейчас предлагаются школьные канцтовары в огромном выборе. Транспортир не исключение. Производители стараются угодить самым требовательным запросам покупателей. Инструменты изготавливают в различной цветовой гамме. Яркие цвета всегда нравятся детям. Порой даже в одном классе не сыскать одинаковых транспортиров, что облегчает при утрате их поиск. Формы и размеры каждый выбирает на свой вкус.
Большинство таких товаров выпускают из пластмассы, и это значительно уменьшает его стоимость. Но есть деревянные и даже железные транспортиры. Как показывает практика, металлические хоть и непрозрачны, но практичнее в том плане, что шкала не стирается, а это позволяет гораздо дольше применять его в действии, с точностью определяя углы.
Транспортир не так востребован школьниками, как линейка, но он сопровождает учеников вплоть до выпускного экзамена. Некоторые из выпускников школы выбирают специальности, которые связаны с измерением и построением углов, проектированием зданий и сооружений, работой с чертежами. В силу своих профессий им постоянно приходится сталкиваться с транспортирами и его производными. Но и бывшие одноклассники нынешних инженеров, порой даже с глубочайшим гуманитарным уклоном, без труда вспомнят навыки обращения с этим предметом и определят количество градусов у любого угла.
Итог
Сегодня современные дети привыкли добывать любую информацию из интернета. Однако он никак не поможет в измерении углов. Лишь только умение пользоваться транспортиром даст возможность правильно их определять. Будущим инженерам и проектировщикам это бесспорно пригодится в работе, да и каждый образованный человек должен обладать навыками работы с транспортирами, поэтому уметь пользоваться таким инструментом должен каждый!
Как правильно определять углы — Инженер ПТО
Измерить угол – значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.
Обычно за единицу измерения углов принимают градус. Градус – это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).
Измерение углов транспортиром
Для измерения углов используют специальный прибор – транспортир:
У транспортира две шкалы – внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:
Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов и пишут: ∠BOC = 60°, ∠MON = 120°.
Для более точного измерения углов используют доли градуса: минуты и секунды. Минута – это угол, равный части градуса. Секунда – это угол, равный части минуты. Минуты обозначают знаком ‘, a секунды – знаком ». Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:
Свойства измерения углов
Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.
Рассмотрим угол AOB:
Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.
Развёрнутый угол равен 180°.
Любой угол имеет определённую величину, большую нуля.
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Минутой называют одну шестидесятую часть градуса.
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « ‘ », а секунды « » ». Имеет место обозначение:
1 ° = 60 ‘ = 3600 » , 1 ‘ = ( 1 60 ) ° , 1 ‘ = 60 » , 1 » = ( 1 60 ) ‘ = ( 1 3600 ) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 ‘ 59 » .
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17 ° 3 ‘ 59 » . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала ( 0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале ( 0 , 90 ) , а тупой – ( 90 , 180 ) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С , С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В . По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А .
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Измерение углов: градусы и радианы
Анна Малкова
Почему полный круг составляет 360 градусов? Что такое радиан и как перевести градусы в радианы? И при чем здесь число ? Статья для тех, кто сдает ЕГЭ или просто интересуется математикой.
Для измерения углов принято использовать две основные единицы: градусы и радианы.
Начнем с привычных градусов.
Полный круг составляет 360 градусов – это мы все знаем.
Да, но почему 360?
В метре 100 сантиметров. В рубле 100 копеек, в килограмме 1000 грамм. Мы привыкли к десятичной системе, и возникла она оттого, что на каждой руке у нас по 5 пальцев, а на двух руках — по 10.
А вот в часе 60 минут, в круге 360 градусов. И в сутках 24 часа. Древние шумеры умудрились придумать двенадцатеричную систему счисления! И при этом они тоже считали по пальцам. Нет, у них не было по 6 пальцев на каждой руке. Просто считали не пальцы, а фаланги четырех пальцев (кроме большого).
Кстати, круг легко делится именно на 6 частей (умеете?). А число 12 (дюжина) делится на 2, 3, 4, 6 и, собственно, 12.
И это не все. Древние шумерские астрономы обнаружили, что в день равноденствия Солнце встает почти точно на Востоке и заходит почти точно на Западе, причем от восхода до заката проходит по небу путь, в 360 раз больший, чем видимый с Земли диаметр Солнца. Небесную полуокружность разделили на 180 градусов.
Точнее, угловой диаметр Солнца равен примерно 32 угловых минуты, то есть чуть больше 0,5 градуса. Он еще и немного меняется в течение года из-за того, что орбита Земли не круговая, а эллиптическая.
Так что утверждение о том, что в День равноденствия Солнце проходит по небу путь, равный 360 своим «шагам» (то есть 360 видимым диаметрам солнца) – верно с некоторой точностью.
Конечно, древние астрономы наблюдали не только за движением Солнца. Они заметили, что яркая планета Юпитер совершает полный оборот вокруг Солнца за 12 лет. Точнее, не 12, а 11,86 лет, но уж очень им хотелось округлить до своего любимого числа.
Да что там Юпитер! Посмотрим на Луну. Юпитер на небе еще и не каждый найдет (а вы сможете?) – зато Луну, особенно полную, трудно не заметить! Месяц – промежуток от полнолуния до полнолуния – равен примерно 29,5 суток. Почти 30, верно?
Наша Земля совершает полный оборот вокруг Солнца за 365 дней (точнее, за 365,242 суток), и это – солнечный год.
И тогда лунный год – это 12 месяцев, в каждом месяце 30 дней (округлили), вот и получается 360 дней в году, почти столько же, сколько в солнечном, в котором 365 дней.
«Может быть, боги хотели сделать в году ровно 360 дней, но им кто-нибудь помешал, вот и получилось 365». Возможно, так и рассуждали древние астрономы, деля круг на 360 частей, 360 градусов. Тем более, что 360 – число, имеющее целых 24 делителя.
Число 360 делится на 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 и 360. Очень удобно делить 360 градусов на части!
Обозначается: 360°. Этот кружок вверху – специальный символ для обозначения градуса.
Есть и другая мера измерения углов – радианная.
1 радиан – центральный угол, опирающийся на дугу, равную радиусу окружности.
Как перевести градусы в радианы и наоборот?
Полный круг – это 360 градусов. Отношение длины окружности к ее диаметру равно числу , приближенно Значит, длина окружности равна где – радиус.
Составим пропорцию. Длина окружности так относится к длине дуги на нашем рисунке, как – к величине угла, опирающегося на эту дугу, то есть к углу в 1 радиан.
1 радиан –
Слева в нашей пропорции углы, справа – длина полной окружности и длина отмеченной на рисунке дуги.
Из этой пропорции получаем, что радиан. Значит, полный круг – это радиан. Тогда полкруга – это радиан, четверть круга (то есть ) – это радиан.
Любой угол, выраженный в градусах, можно перевести в радианы. И наоборот, 1 радиан приблизительно равен 57 градусам.
Радианная мера углов
§ 11. Радианная мера углов
1. Понятие угла
В геометрии
Угол — геометрическая фигура, образованная двумя лучами, которые выходят из одной точки.
В тригонометрии*
Угол — фигура, образованная при повороте луча на плоскости около начальной точки.
2. Измерение углов
Градусная мера углачасть развернутого угла)
Каждому углу ставится в соответствие градусная мера α ∈ [0°; 180°].
Каждому углу как фигуре ставится в соответствие угол поворота, с помощью которого образован этот угол. Угол поворота
α ∈ (–×; +×).
Объяснение и обоснование
1. Понятие угла. В курсе геометрии угол определяется как геометрическая фигура, образованная двумя лучами, которые выходят из одной точки. Например, угол AOB, изображенный в первом пункте таблицы 16, — это угол, образованный лучами OA и OB.
Угол можно рассматривать также как результат поворота луча на плоскости около начальной точки. Например, поворачивая луч OA около точки O от начального положения OA до конечного положения OB, также получим угол AOB. Заметим, что достичь конечного положения ОВ можно при повороте луча OA как по часовой стрелке, так и против нее.
2. Измерение углов. Данные выше различные определения угла приводят к различному пониманию измерения углов.
В курсе геометрии каждому углу соответствует его градусная мера, которая может находиться только в пределах от 0° до 180°, и поэтому, например, для прямого угла AOB его мера записывается однозначно: ∠ AOB = 90° (1° — это 1/180 часть развернутого угла).
При измерении углов поворота договорились, что направление поворота против часовой стрелки считается положительным, а по часовой стрелке — отрицательным.
Поэтому при измерении углов, образованных при повороте луча около начальной точки, мы можем получить как положительные, так и отрицательные значения углов поворота. Например, если угол AOB, в котором лучи ОА и ОВ являются взаимно перпендикулярными, получен при повороте луча OA на угол 90° против часовой стрелки, то значение угла поворота β (см. соответствующий рисунок в пункте 2 табл. 16) равно +90° (или просто 90°). Если тот же угол AOB получен при повороте луча OA на угол 270° по часовой стрелке (понятно, что полный оборот — это 360°), то значение угла поворота γ равно (–270°). Этот же угол AOB можно получить также при повороте луча OA против часовой стрелки на 90° и еще на полный оборот; в этом случае значение угла поворота ϕ равно 90° + 360°, то есть 450° и т. д.
Выбрав как значение угла поворота произвольное отрицательное или положительное число (градусов), мы всегда можем повернуть луч OA (по часовой стрелке или против нее) и получить соответствующий угол AOB. Таким образом, величина угла поворота (в градусах) может принимать все действительные значения от.
Для измерения углов принимают определенный угол за единицу измерения и с ее помощью измеряют другие углы.
За единицу измерения можно принять любой угол, например один градус (1°) — 1/180 часть развернутого угла.
В технике за единицу измерения углов принимают полный оборот (заметим, что 1 градус — это 1/360 часть полного оборота).
В мореходстве за единицу измерения углов принимают румб, равный 1/32 час ти полного оборота.
В математике и физике, кроме градусной меры углов, используется также радианная мера углов.
Если рассмотреть некоторую окружность,
то 1 радиан — это центральный угол, соответствующий дуге, длина которой равна радиусу окружности.
Таким образом, если угол AOB равен одному радиану (рис. 59), то это означает, что ∪AB = OA = R.
Установим связь между радианной и градусной мерами углов. Центральному развернутому углу AOC, с градусной мерой 180°, соответствует полуокружность, то есть дуга, длина которой равна πR, а углу в один радиан — дуга длиной R. Итак, радианная мера развернутого угла AOC равна радиан. Таким образом, одному и тому же развернутому углу АОС соответствует градусная мера 180° и радианная мера π радиан. Это соответствие часто записывают так:
Задача 1 Выразите в радианах величины углов, градусная мера которых равна: 30°; 45°; 60°; 90°; 270°; 360°.
Поскольку 30° — это 1/6часть угла 180°, то из соответствия 180° = π (рад)
получаем, что 30°=6/π (рад).
Аналогично можно вычислить и величины других углов.
В общем случае учитываем, что 1°=π/180 радиан, тогда:
Поскольку радианными мерами рассмотренных углов приходится пользоваться достаточно часто, запишем полученные результаты в виде справочной таблицы:
Замечание. Чаще всего при записи радианной меры углов наименование единицы измерения «радиан» (или сокращенно рад) не пишут, но подразумевают его. Например, вместо равенства 90 2 °=π радиан пишут иногда 90 °=π/2 .
Задача 2 Выразите в градусах величины углов, радианнная мера которых равна: π/10 ; 2π/3 ; 3π/4 ; 5.
Поскольку π/10 — это 1/10 часть угла π, то из соответствия π = 180° получаем, что π/10=18° . Аналогично можно вычислить и величины углов 2π /3 и 3π/4 .
В общем случае учитываем, что 1 радиан=180°/π , тогда:
Отметим, что далее в этом разделе будет рассматриваться в основном радианная мера угла и утверждения будут доказаны для радианной меры угла. Однако их можно переформулировать и для градусной меры угла, пользуясь приведенными выше соотношениями.
Условимся далее вместо слов «угол, радианная мера которого равна α радиан» говорить коротко «угол α».
Вопросы для контроля
1. Объясните, как можно определить угол с помощью поворота луча. Как при таком определении измеряются углы?
2. Как вы понимаете такие утверждения: «Величина угла равна 450°», «Величина угла равна (–225°)»? Изобразите эти углы.
3. Как можно определить угол в 1°?
4. Дайте определение угла в 1 радиан.
5. Чему равна градусная мера угла в π радиан?
6. Объясните на примерах, как по радианной мере угла найти его градусную меру и наоборот — по градусной мере угла найти его радианную меру.
Упражнения
1°. Изобразите угол, образованный поворотом луча OA около точки O на: 1) 270°; 2) –270°; 3) 720°;
4) –90°; 5) 225°; 6) –45°;
7) 540°; 8) –180°; 9) 360°; 10) –60°.
2°. Чему равны градусные и радианные меры углов поворота, показанных на рисунке 60?
3. Выразите в радианной мере величины углов, градусная мера которых равна:
1 °) 225°; 2°) 36°; 3) 100°; 4) –240°; 5) –22,5°; 6) –150°.
4. Выразите в градусной мере величины углов, радианная мера которых равна:
1) 3π; 2) 3 4 π; 3) −2 5 π;
4) 7 6 π; 5) − π 18 ;
6) 11 6 π;7) −π 8 ; 8) 3.
5. С помощью калькулятора (или таблиц) найдите радианные меры углов, градусная мера которых равна:
1) 27°; 2) 132°; 3) 43°; 4) 114°.
6. С помощью калькулятора (или таблиц) найдите градусные меры углов, радианная мера которых равна:
1) 0,5585; 2) 0,8098; 3) 3,1416; 4) 4,4454.
8.1: Измерение угла — Математика LibreTexts
Угол — это мера размера отверстия двух пересекающихся линий. VERTEX является точкой пересечения, а линии, образующие проем, называются SIDES .
Угол можно вызвать по
3 буквы с вершиной посередине: \ (\ angle ABC \) или только вершиной \ (\ angle B \), либо числом или буквой, помещенными внутри угла.
В круге 360 градусов. Углы измеряются в градусах.
A Прямой угол составляет 90 градусов или 1/4 окружности. Right Angle будет выглядеть следующим образом.
Острый угол — это угол меньше 90 градусов. Ниже приведены примеры острых углов
.
Тупой угол — это угол больше 90 градусов и меньше 180 градусов. Ниже приведены примеры тупых углов.
A Прямой угол — это угол, равный 180 градусам.
Вертикальные углы
При пересечении двух прямых линий они образуют четыре угла.
Предположим, что \ (\ angle A \) равен 65 градусам, \ (\ angle B \) равен 115 градусам, \ (\ angle C \) равен 65 градусам, а \ (\ angle D \) равен 115 градусам
Вы заметили, что противоположные углы равны при измерении? Противоположные углы также называются Вертикальные углы .Когда две прямые линии пересекаются или пересекаются, вертикальных углов равны , всегда равняется . Прямой угол — 180 градусов.
Углы W и X образуют прямую линию, вместе они составляют 180 градусов.
Они также известны как Смежные углы . Смежные углы в сумме составляют 180 градусов. Смежные углы также равны
.
- \ (\ angle Y \) и \ (\ angle Z \),
- \ (\ угол W \) и \ (\ угол Y \)
- \ (\ угол X \) и \ (\ угол Z \).
Сумма трех углов треугольника всегда составляет 180 градусов.
Линии Z и Y параллельны друг другу. Линия P, пересекающая обе линии, называется Transversal .
\ (\ angle C \) и \ (\ angle F \) называются Alternate Internal Angles ; Они равны по размеру.
\ (\ angle D \) и \ (\ angle E \) также называются Alternate Internal Angles .
Если угол равен 70 градусам, то \ (\ angle P \) будет равен 110 градусам, их сумма равна 180 градусам.
- \ (\ angle P \) и \ (\ angle Q \) — противоположные углы, поэтому они равны 110 градусам, потому что вертикальные углы равны друг другу.
- \ (\ angle P \) и \ (\ angle T \) и соответствующие углы, поэтому оба они равны 110 градусам.
- \ (\ angle W \) равняется 70 градусам, потому что \ (\ angle T \) плюс \ (\ angle W \) должно равняться в сумме 180 градусам.
Измерение углов
Измерение углов
Понятие угла
Понятие угла — одно из важнейших понятий в геометрии.Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов .
Есть две обычно используемые единицы измерения углов. Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. Пока мы будем рассматривать только углы от 0 ° до 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы. Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минутами. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 «. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды. |
Части градуса теперь обычно обозначаются десятичной дробью. Например, семь с половиной градусов теперь обычно пишут как 7,5 & deg.
Когда один угол рисуется на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), одна сторона угла вдоль x ось, а другая сторона выше оси x .
Радианы
Другое распространенное измерение углов — радианы.Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла. Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. Окружность всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно, 1 ° равняется π /180 радиан и 1 радиан равен 180/ π градусов Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах.Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор. |
Краткая заметка об истории радианов
Хотя слово «радиан» было придумано Томасом Мьюиром и / или Джеймсом Томпсоном около 1870 года, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей работе Elements of Algebra явно сказал, что углы следует измерять по длине дуги, отрезанной в единичной окружности.Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией.
e iθ = cos θ + i sin θ
где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается в виде отношения. Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, тогда мера в радианах равна 1.5.
Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r, умноженному на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.
Радианы и площадь сектора
Сектор круга — это часть круга, ограниченная двумя радиусами и дугой круга, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и углу θ между радиусами, когда он измеряется в радианах.Поскольку площадь всего круга составляет πr 2 , а сектор — это весь круг, так как угол θ равен 2 π , поэтому
Углы общие
Ниже приведена таблица общих углов как при измерении в градусах, так и при измерении радиан. Обратите внимание, что измерение в радианах дано в терминах π . Его, конечно, можно было бы указать в десятичной дроби, но радианы часто появляются с коэффициентом 90 · 106 π 90 · 107.
.
| Уголок | градусов | Радианы |
|---|---|---|
| 90 ° | π /2 | |
| 60 ° | π /3 | |
| 45 ° | π /4 | |
| 30 ° | π /6 |
Упражнения
Эдвин С.Кроули написал книгу Тысяча упражнений в плоской и сферической тригонометрии, Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.
Кроули использовал не десятичные дроби для дробей градуса, а минуты и секунды.
Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, некоторые подсказки для решения упражнений, а в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.
(б). 36 ° 12 ‘.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, , чтобы найти длину продолжающейся дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.
4. Учитывая длину дуги l и радиус r, , чтобы найти угол, стянутый в центре.
(а). л = 0,16296, л = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус составляет 3200 футов.
7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.
9. На сколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?
14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?
23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?
Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 дюймов.
3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «составляет 0,0051778 радиана. Затем умножьте его на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Их можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусного измерения в радиан .Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.
6. Длина дуги равна радиусу, умноженному на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.
9. У вас есть круг радиусом 3956 миль и дуга этого круга длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы узнать, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре. (Это не совсем часть дуги, но довольно близко). Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?
ответы
1. (а). 0,2176. (б). 0,6318.
2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535
радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.
5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.
6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.
7. Угол a = 0,16776 радиана. Разница в длине составляет
2102,5 a — 1997,5 a , что равно 5 a. Таким образом, ответ составляет 0,84 фута, что с точностью до дюйма составляет 10 дюймов.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.
10. Одна минута = 0,0002909 радиан. 1.15075 миль = 6076 футов.Следовательно, одна секунда будет соответствовать 101,3 фута.
14. a = л / об = 1,742 / 5,782 = 0,3013 радиан = 17,26 ° = 17 ° 16 ‘.
23. Угол a равен 8,5 ‘, что составляет 0,00247 радиана. Таким образом, радиус равен r = л / год = 50 / 0,00247 = 20222 ‘= 3,83 мили, почти четыре мили.
Насчет цифр точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах.Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.
Другой пример см. В задаче 3 (a). Данные 0 ° 17’48 «и 6.2935 с точностью до 4 и 5 знаков соответственно. Следовательно, ответ должен быть дан только с точностью до 4 цифр, так как ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не включая ведущие нули) до 0,03259.
Хотя окончательные ответы должны быть выражены с соответствующим числом цифр точности, вы все равно должны сохранять все цифры для промежуточных вычислений.
градусов как единица измерения угла
градус как единица измерения угла — Math Open Reference
Определение: мера
угол.
Один градус — это одна 360-я часть полного круга.
Попробуй это
Отрегулируйте угол ниже, перетащив оранжевый на R. Обратите внимание на количество градусов для любого конкретного угла.
Измерение угла
В геометрии
угол.
измеряется в градусах, где полный круг равен 360 градусам.Небольшой угол может составлять около 30 градусов.
Обычно, когда требуется более точная мера, мы просто добавляем десятичные разряды к градусам. Например 45,12 °
Маленький кружок после числа означает «градусы». Таким образом, это будет произноситься как «сорок пять целых два десятых градуса».
Градусов — Минут — Секунды
При измерении широты и долготы каждый градус делится на минуты и секунды.
Степень делится на 60 минут. Для более точных измерений минута снова делится на 60 секунд,
Однако эта последняя мера настолько мала, что используется только там, где углы
поданный
на экстремальных расстояниях, таких как астрономические измерения и измерения широты и долготы.
Эти минуты и секунды (как ни странно) не имеют ничего общего со временем. Они просто все меньшие и меньшие части градуса.
См. Также Градусы — Минуты — Калькулятор секунд.
для калькулятора, который может складывать и вычитать углы в этой форме.
| Блок | Письменный | Выражено |
| Градусов | С кружком после номера. Пример 61 ° | «61 градус» |
| Минуты | С маленьким тире после номера. Пример 34 ° 21 ‘ | «34 градуса, 21 минута» |
| Секунды | С двумя маленькими черточками. Пример 32 ° 34 ’44’ ‘ | «32 градуса, 34 минуты, 44 секунды» |
Когда используются только минуты и секунды, мы обычно говорим «угловые минуты» и «угловые секунды», чтобы избежать путаницы с единицами времени.
В каком направлении измерять?
На рисунке выше отрегулируйте точку R так, чтобы линия пересекала точку с отметкой 315 °.Начиная с Q и идя против часовой стрелки, мы видим, что размер равен 315 °. Но если бы мы пошли по часовой стрелке от Q, это было бы 45 ° (360-315). Что правильно?
Оба они есть, но по соглашению предполагается меньший. Поэтому в этих условиях угол в центре составляет 45 °.
Большая мера (315 °) называется
угол рефлекса RPQ.
Углы, которые вы должны знать
На приведенном выше рисунке показано, как выглядят различные угловые меры, измеренные в градусах.В общем, вы должны уметь
чтобы визуально оценить любой угол с точностью до 15 °, и вы должны быть в состоянии распознать общие углы (показаны красным) на месте и сами зарисовать их.
Прочие меры
Радианы
Угол может быть измерен в радианах, где полный круг составляет 2 пи радиана (около 6,28).
Это широко используется в тригонометрии.Грады
В некоторых маркшейдерских работах используется град. В круге 400 градусов, поэтому прямой угол равен 100 градусам.Вы редко увидите этот агрегат. Думайте об оценках как о «метрических градусах».
Морские углы
Судовые навигаторы используют углы, которые измеряются несколько иначе, с помощью системы, разработанной сотни лет назад для Nautical Alamanac — книги навигационных таблиц.
Каждый градус, как обычно, делится на 60 минут, но секунд нет.
Вместо этого минуты выражаются в десятичном формате. Например, 23 ° 34,62 ‘читается как «23 градуса 34,62 минуты.
См. Также «Калькулятор морского угла».
Что попробовать
- На рисунке выше нажмите «Скрыть детали».
- Отрегулируйте положение точки R
- Оценить угол RPQ
- Нажмите «Показать подробности», чтобы узнать, насколько близко вы подошли
- Повторить.
Вы должны быть особенно в состоянии оценить углы, близкие к красным на рисунке выше, поскольку они часто встречаются в геометрии.
Другие ракурсы
Общий
Угловые типы
Угловые отношения
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Измерьте и классифицируйте угол (геометрия, точки, линии, плоскости и углы) — Mathplanet
Линия, имеющая одну определенную конечную точку, называется лучом и продолжается бесконечно в одном направлении. Луч назван в честь конечной точки и другой точки на луче, например.
$$ \ overset {\ rightarrow} {AB} $$
Угол, который образуется между двумя лучами с одинаковой конечной точкой, измеряется в градусах. Точка называется вершиной
.
Вершина записывается как
$$ \ Измеренный угол CAB $$
В алгебре мы использовали координатную плоскость для построения графиков и решения уравнений.Вы можете наносить линии, отрезки, лучи и углы на координатную плоскость.
В координатной плоскости выше у нас есть два луча
$$ \ overset {\ rightarrow} {BA} \: \: и \: \: \ overset {\ rightarrow} {BD} $$
образуют угол с вершиной в точке B.
Вы можете использовать координатную плоскость для измерения длины отрезка. Точка B находится в точках (-2, -2) и C (1,2). Расстояние между двумя точками составляет 1 — (-2) = 3 единицы.
Углы могут быть прямыми, прямыми, острыми или тупыми.
Угол — это часть окружности, в которой весь круг равен 360 °. Прямой угол равен половине круга и равен 180 °, тогда как прямой угол равен четверти круга и равен 90 °.
Вы измеряете угол с помощью транспортира.
Два угла с одинаковой мерой называются конгруэнтными углами. Конгруэнтные углы обозначены как
.
$$ \ угол A \ конг \ угол B $$
Или может быть показан дугой на рисунке, чтобы указать, какие углы совпадают.{\ circ} $
Видеоурок
Измерьте размер уголка
Углы измерения
| Важность | Разные системы
18 ноября 2020
Время чтения: 4 минуты
Линии и углы — первые понятия геометрии, которые изучает студент. Линия — это набор точек, а угол образуется при пересечении двух лучей. Луч — это линия, которая бесконечно проходит в одном направлении.
Когда два луча исходят из общей точки, наклон одного луча к другому называется углом.
Также читайте:
Геометрия дает учащимся возможность рисовать и изучать 2D и 3D формы. Но с чего это начинается? Для измерения угла могут потребоваться простые математические уравнения или более сложная геометрия.
Для измерения угла обычно нужен транспортир.Загрузите PDF-файл ниже, чтобы узнать, почему важны углы и разные системы измерения угла.
| 📥 | Как найти величину угла? | Загрузить |
Почему важны углы?
Углы используются в самых разных формах: от забавных, например, в игре «Карром», до более сложных, например, движения планет.
Строительство, архитектура, спорт, инженерия, искусство, танцы и т. Д. Используют понятие углов. Помимо этого, ученые и астрономы полагаются на углы, под которыми небесные тела делают, чтобы изучить их движение и прийти к конкретным выводам.
При измерении вы будете иметь дело с вершиной угла, где две линии встречаются, образуя угол. Углы измеряются в градусах. Измерение углов может помочь нам лучше подготовиться к работе с числами и измерениями, а также к использованию наших визуальных способностей.
Примеры вопросов и ответов
Давайте рассмотрим несколько примеров вопросов и ответов о том, как найти меру угла —
Q.1 Какова сумма внутренних углов треугольника?
Ответ — Сумма внутренних углов треугольника составляет 180 градусов.
Q.2 Два внутренних угла треугольника составляют 50 и 45. Какая наибольшая мера любого из его внешних углов?
Ответ — Внутренние углы треугольника должны иметь меры, сумма которых равна 180, поэтому размер третьего угла должен быть
.
180 — (50 + 45) = 85
Согласно теореме о внешнем угле треугольника, внешний угол треугольника измеряет сумму его удаленных внутренних углов; поэтому, чтобы получить наибольшую меру любого внешнего угла, мы добавляем две наибольшие меры внутреннего угла:
50 + 85 = 135
Q.3 Два угла являются дополнительными и имеют соотношение 1: 4. Каков размер меньшего угла?
Ответ — Поскольку углы дополнительные, их сумма составляет 180 градусов. Поскольку их соотношение составляет 1: 4, можно записать следующее выражение:
х + 4х = 180
5x = 180
х = 36
Q.4 В данном треугольнике углы находятся в соотношении 1: 3: 5. Какого размера средний угол?
Ответ — Сумма углов треугольника равна 180
, и учитывая, что углы находятся в соотношении 1: 3: 5, пусть мера наименьшего угла будет
x, то можно записать следующее выражение:
х + 3х + 5х = 180
9x = 180
х = 20
Если наименьший угол равен 20 градусам, тогда, учитывая, что средний угол находится в соотношении 1: 3, средний угол будет в 3 раза больше, или 60 градусов.
Q.5 Сумма двух внутренних углов треугольника составляет 64 градуса. Какова мера другого угла?
Ответ — Сумма трех углов треугольника составляет 180 градусов. Вычтите 64 градуса, чтобы определить третий угол.
180–64 = 116
Знаете ли вы стандартные системы измерения углов?
Вот различные стандартные системы, используемые для измерения углов. Мы упростили их для вас, чтобы помочь вашим ученикам
1.Степень
Градус — это измерение плоского угла, составляющего 1/360 полного оборота. Обычно обозначается цифрой °.
Почему 360 ° считается углом для одного полного поворота?
Считается, что вавилоняне изобрели градус и всегда считали по основанию 60. Вот где родились первые идеи 360. Его считали из-за того, что он легко делится на множество чисел. Например, 360 делится на все числа от 1 до 10, кроме 7.Наука также подтверждает, что Земле требуется около 365 дней, чтобы совершить один оборот вокруг Солнца. В большинстве основных календарей в году около 360 дней.
градусов измеряются с помощью транспортира и являются одним из наиболее распространенных методов измерения углов.
2. Радиан
Радианная мера угла определяется как отношение длины дуги, которую угол образует окружность, к длине радиуса той же окружности.
Это соотношение даст вам величину угла в радианах.
В радианах нет единицы. Почему? Поскольку это соотношение двух длин, следовательно, единицы отменяются.
3. Революция
Оборот считается самой простой и естественной единицей измерения геометрических углов. Революции помогают учащимся понять более глубокое значение углов. Это потому, что угол — это, по сути, подразделение круга, а не сумма нескольких градусов.Например, ученикам легче понять, что «прямой угол составляет четверть круга», чем «прямой угол равен 90 °
.
Знакомство учащихся с поворотами и градусами поможет им лучше понять концепцию углов. Вот иллюстрация, с помощью которой вы можете пояснить разницу между тремя системами измерения углов
.
Помимо стандартных систем, хорошо на раннем этапе у учащегося сформировать представление о том, что единицей измерения угла является угол.Его не «нужно» измерять в градусах. Они могут создать свою собственную систему измерения и использовать ее для измерения углов.
Учащимся легче развить чувство измерения угла с помощью клина, а не транспортира. Транспортир с бумажным клином можно сделать, сложив круг пополам четыре раза, пока не будут сформированы 16 клиньев (или секторов). Если бумага прозрачная, то ее можно положить на угол многоугольника или угловой луч. Количество клиньев можно подсчитать.
Поощряйте своих учеников открывать новые методы измерения углов, и кто знает, в ближайшие годы их метод может стать традиционным.
Сводка
Суммируем:
- Два луча с одинаковой конечной точкой образуют угол. Углы можно найти в различных объектах вокруг нас, будь то ножницы, хоккейная клюшка или стул.
- Точка, в которой они пересекаются, называется вершиной, которая является общей конечной точкой лучей / отрезков линии.При названии угла вершина всегда находится в центре.
- Измерение углов может помочь улучшить пространственное понимание и взаимосвязь между числами и измерениями, они не только полезны в учебе, но и изучение углов помогает нам понимать и использовать вещи вокруг нас.
Мы надеемся, что эта статья о том, как найти меру угла, показалась вам интересной и информативной. Не стесняйтесь поделиться этой статьей. Убедитесь, что вы регулярно пересматриваете эти концепции, пока они не будут полностью поняты, поскольку они являются базовыми и основополагающими.Регулярно посвящайте от 30 до 45 минут изучению, пониманию и практике концепций. Вы можете узнать больше об углах у нас, запишитесь на бесплатное занятие.
О компании Cuemath
Cuemath, удобная для учащихся платформа математики и кодирования, проводит регулярные онлайн-классы для преподавателей и развития навыков, а их приложение Mental Math для iOS и Android представляет собой универсальное решение для детей, развивающее несколько навыков. Ознакомьтесь со структурой Cuemath Fee и подпишитесь на бесплатную пробную версию.
Часто задаваемые вопросы (FAQ)
Как найти угол в окружности?
Окружность имеет в сумме 360 градусов от центра до центра, если центральный угол, определяющий сектор, имеет угловую меру 60 градусов, тогда сектор занимает 60/360 или 1/6 градусов от всех наоборот. В этом случае сектор составляет 1/6 площади всего круга.
Как найти размер дуги с вписанным углом?
Вписанный угол имеет вершину на окружности, а стороны угла лежат на двух хордах окружности.Размер вписанного угла составляет половину дуги, которую две стороны вырезают из круга.
Как найти меру внутреннего угла?
Вписанный угол имеет вершину на окружности, а стороны угла лежат на двух хордах окружности. Размер вписанного угла составляет половину дуги, которую две стороны вырезают из круга.
Что такое градусная мера и как найти градусную меру угла?
В этой системе угол измеряется в градусах, минутах и секундах.Степень обозначается как º.
1 прямой угол = 90 градусов или 90 градусов.
Внешние ссылки
Играть в угловые игры — SplashLearn
Построение углов — Math Only Math
Углы измерения
| Помощь с математикой
Результаты обучения
К концу этого урока ваши дети смогут понять, что представляют собой углы и как они измеряются в градусах.
Разминка
Многие учащиеся проходят весь курс обучения геометрии, даже не понимая, что представляют собой углы. Это приводит к замешательству и разочарованию. Понимая более широкую картину, весь предмет становится намного яснее. Угол на самом деле представляет собой отрезок круга.
Поняв размер всего круга, легко понять и распознать, какие части этого круга представляют. В этом уроке вы будете исследовать углы как части круга.
Лист предварительной оценки
Попросите ваших детей пройти предварительный тест, указанный ниже, чтобы узнать, готовы ли они к этому уроку. Если они наберут 7 или меньше правильных ответов, просмотрите вместе с ними фрагменты круга, прежде чем продолжить урок.
Основной урок: Измерение углов
Круг — это круглая фигура, образованная точками, находящимися на одинаковом расстоянии от центральной точки фигуры. Круг состоит из 360 равных участков. Используя единицу измерения один «градус» для каждого участка, мы говорим, что круг имеет 360 градусов.Символ ° часто используется вместо слова «градусы».
Типичный угол, который вы видите, когда изучаете геометрию, — это не что иное, как отрезок, взятый из полного круга. Конечная точка угла, точка, где два луча соединяются, образуя угол, совпадает с центральной точкой круга. Если вы представите, как закрашиваете остальную часть круга вокруг заданного вам угла, это поможет вам лучше понять размер вашего угла.
Все углы составляют 360 ° или меньше, так как это максимальное количество градусов в полном круге.
Ваши дети должны познакомиться с кругами и круговыми диаграммами и понять, что угол — это кусок круга, как кусок пирога — это кусок целого пирога.
Напомните своим детям представить себе круг, когда они видят угол. Они могут думать об угле, который они рассматривают, как о срезе или клине, вырезанном из полного круга. Поскольку полный круг имеет размер 360 °, любой отрезок, взятый из него, должен иметь размер менее 360 °.
Классифицирующие углы
Углы классифицируются или сортируются по размеру.Некоторые названия, используемые для классификации углов, были показаны выше, но некоторые из них являются новыми. Давайте посмотрим на их все вместе:
Острые углы: углов меньше 90 °
Прямые углы: угла с точностью до 90 °
Тупые углы: угла, превышающие 90 °
Прямые углы: угла с точностью до 180 °
Углы отражения: угла, превышающие 180 °
Полное вращение: угла, которые измеряют точно 360 °
Резюме
- Углы — это участки окружности.
- Окружность или полное вращение составляет 360 °.
- Четверть круга или прямой угол равны 90 °.
- Полукруг или линия имеет 180 °.
- Три четверти круга составляют 270 °.
- Углы меньше 90 ° острые.
- Углы больше 90 ° тупые.
Контрольные вопросы
Просмотрите приведенные выше моменты резюме со своими детьми, а затем распечатайте последующий тест.
Как минимум 7 из 10 правильных ответов покажут, что ваши дети готовы перейти к следующему уроку: Транспортиры
углов
Уголки используются в повседневной жизни.Инженеры и архитекторы используют углы для
конструкции, дороги, здания и спортивные сооружения. Спортсмены используют углы, чтобы
повысить их производительность. Плотники используют углы для изготовления стульев, столов и
диваны. Художники используют свои знания углов для набросков портретов и
картины.
Если две прямые встречаются (или пересекаются) в одной точке, образуется угол .
Точка пересечения линий называется вершиной .
Угол показан ниже.
Линии AB и AC пересекаются в точке A , образуя
угол. Точка A — это вершина угла, а прямые,
Встречаются, чтобы образовать угол, называемые плечами угла .
Именование углов
Размер уголка
Величина поворота от одного плеча угла к другому называется
размер уголка .
Размер угла измеряется в градусах ; и используемый символ
для представления степени есть. В полном обороте (или круге) 360.
Примечание:
градусов определяется так, что угол одного полного поворота (или
круг) составляет 360 градусов.
Измерительные углы
Транспортир используется для измерения углов. В этом разделе мы будем
рассмотрите возможность использования транспортира в форме полукруга и двух
шкалы от 0 до 180.
Две шкалы позволяют нам легко измерять
углы обращены в разные стороны.
Чтобы измерить размер угла ABC , поместите транспортир над
угол так, чтобы центр транспортира находился прямо над углом
вершина, B; а базовая линия транспортира проходит вдоль кронштейна, BA ,
угла.
Мы используем внутреннюю шкалу для измерения угла ABC , поскольку рычаг AB проходит через ноль внутренней шкалы . Следующий
внутренняя шкала вокруг транспортира, мы обнаруживаем, что другая рука, BC ,
проходит через внутреннюю шкалу на 60. Таким образом, размер угла ABC равен
60 градусов.Запишем это так:
Чтобы измерить размер угла PQR , поместите транспортир над
угол так, чтобы центр транспортира находился прямо над углом
вершина, Q ; а базовая линия транспортира проходит вдоль руки, PQ ,
угла.
Мы используем внешнюю шкалу для измерения угла PQR , поскольку рычаг PQ проходит через ноль внешней шкалы шкалы .Следующий
внешняя шкала вокруг транспортира, мы обнаруживаем, что другая рука, QR ,
проходит через внешнюю шкалу на 120. Таким образом, размер угла PQR равен
120 градусов. Запишем это так:
Типы углов
Углы классифицируются по размеру.
Острый угол больше 0 и меньше 90.

 То есть, выражение B3/(B3/B2) определяет, во сколько раз скорость минутной стрелки превышает скорость часовой стрелки.
То есть, выражение B3/(B3/B2) определяет, во сколько раз скорость минутной стрелки превышает скорость часовой стрелки.