Расчет трансформатора — audiohobby.ru
Программный (он-лайн) расчет тороидального трансформатора, позволит налету экспериментировать с параметрами и сократить время на разработку. Также можно рассчитать и по формулам, они приведены ниже.
Описание вводимых и расчётных полей программы:
- — поле светло-голубого цвета – исходные данные для расчёта,
-
— поле жёлтого цвета заполнять не требуется – так как данные автоматически выбираются из справочных таблиц, в случае клика ,
поле меняет цвет на светло-голубой и позволяет ввести собственные значение, -
— поле зелёного цвета – рассчитанное значение.
Sст ф — площадь поперечного сечения магнитопровода. Рассчитывается по формуле:
Sст = h * (D – d)/2.
Sок ф – фактическая площадь окна в имеющемся магнитопроводе. Рассчитывается по формуле:
Рассчитывается по формуле:
Sок = π * d2 / 4.
Зная эти значения, можно рассчитать ориентировочную мощность трансформатора:
Pc max = Bmax *J * Кок * Кст * Sст * Sок / 0.901
J — Плотность тока, см. табл:
| Конструкция магнитопровода | Плотность тока J, [а/мм кв.] при Рвых, [Вт] | ||||
|---|---|---|---|---|---|
| 2-15 | 15-50 | 50-150 | 150-300 | 300-1000 | |
| Кольцевая | 5-4,5 | 4,5-3,5 | 3,5 | 3,0 | |
Вмах — магнитная индукция, см. табл:
| Конструкция магнитопровода | Магнитная индукция Вмах, [Тл] при Рвых, [Вт] | ||||
|---|---|---|---|---|---|
| 5-15 | 15-50 | 50-150 | 150-300 | 300-1000 | |
| Тор | 1,7 | 1,7 | 1,7 | 1,65 | 1,6 |
Кок — коэффициент заполнения окна, см.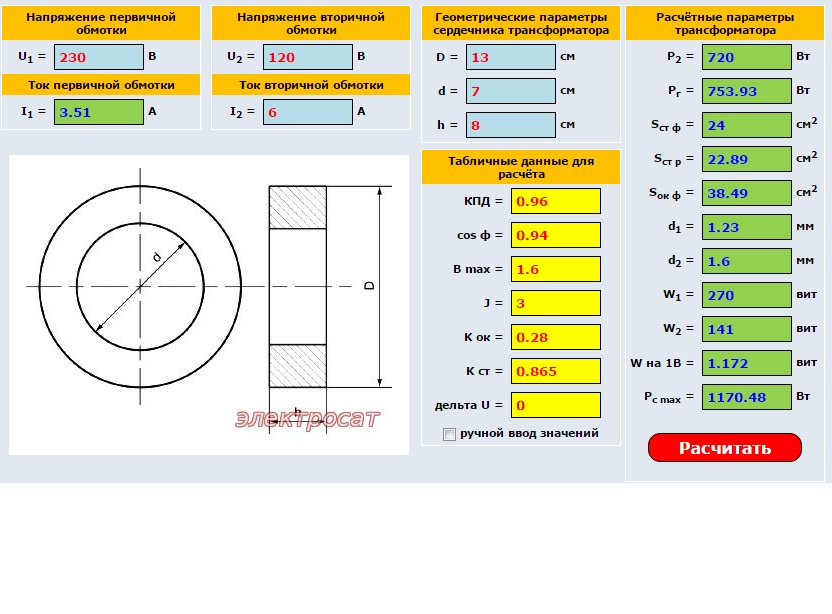 табл:
табл:
| Конструкция магнитопровода | Коэффициент заполнения окна Кок при Рвых, [Вт] | ||||
|---|---|---|---|---|---|
| 5-15 | 15-50 | 50-150 | 150-300 | 300-1000 | |
| Тор | 0,18-0,20 | 0,20-0,26 | 0,26-0,27 | 0,27-0,28 | |
Кст — коэффициент заполнения магнитопровода сталью, см. табл.
| Конструкция магнитопровода | Коэффициент заполнения Кст при толщине стали, мм | ||||
|---|---|---|---|---|---|
| 0,08 | 0,1 | 0,15 | 0,2 | 0,35 | |
| Тор | 0,85 | 0,88 | |||
принцип работы, сечение сердечника, преимущества эксплуатации
Высококачественные трансформаторы широко используются в различных отраслях. Многие мастера ценят такие агрегаты за то, что они достаточно компактны и легки, а вот коэффициент полезного действия находится на высоком уровне. Такие характеристики особенно важны в сварочных аппаратах и стабилизаторах напряжения. Но чтобы такой агрегат исправно работал, нужно правильно рассчитать тороидальный трансформатор.
Многие мастера ценят такие агрегаты за то, что они достаточно компактны и легки, а вот коэффициент полезного действия находится на высоком уровне. Такие характеристики особенно важны в сварочных аппаратах и стабилизаторах напряжения. Но чтобы такой агрегат исправно работал, нужно правильно рассчитать тороидальный трансформатор.
Краткое описание
Современные производители занимаются промышленным изготовлением нескольких разновидностей магнитопроводов для трансформаторов — броневого, стержневого, тороидального. Если сравнивать их эксплуатационные характеристики и сферы использования, то более эффективным можно считать последний вариант. Всё дело в том, что такое устройство обладает исключительно положительными параметрами, благодаря чему активно применяется в современной промышленности.
Высокая производительность и длительный эксплуатационный срок повлияли на то, что сейчас тороидальный трансформатор является базовым элементом в осветительной технике, стабилизаторах напряжения, источниках бесперебойного питания, радиотехнике, а также медицинском и диагностическом оборудовании.
Сами производители утверждают, что такой агрегат представлен в виде однофазной установки, которая может как понижать, так и повышать мощность. Для качественной эксплуатации трансформатор оборудован мощным сердечником с двумя и более обмотками. Но принцип его эксплуатации ничем не отличается от тех моделей, которые оснащены броневой или стержневой намоткой.
В независимости от эксплуатационных характеристик, трансформатор — это устройство, главная задача которого основана на преобразовании электроэнергии из одной величины в другую. Однако даже самые минимальные изменения в конструктивном исполнении могут существенно изменить итоговые размеры и вес электрической установки. Благодаря этому, технико-экономические параметры будут только возрастать.
Основные преимущества
У такого трансформатора магнитопровод имеет форму тороида, иными словами — все кольца отличаются прямоугольным сечением.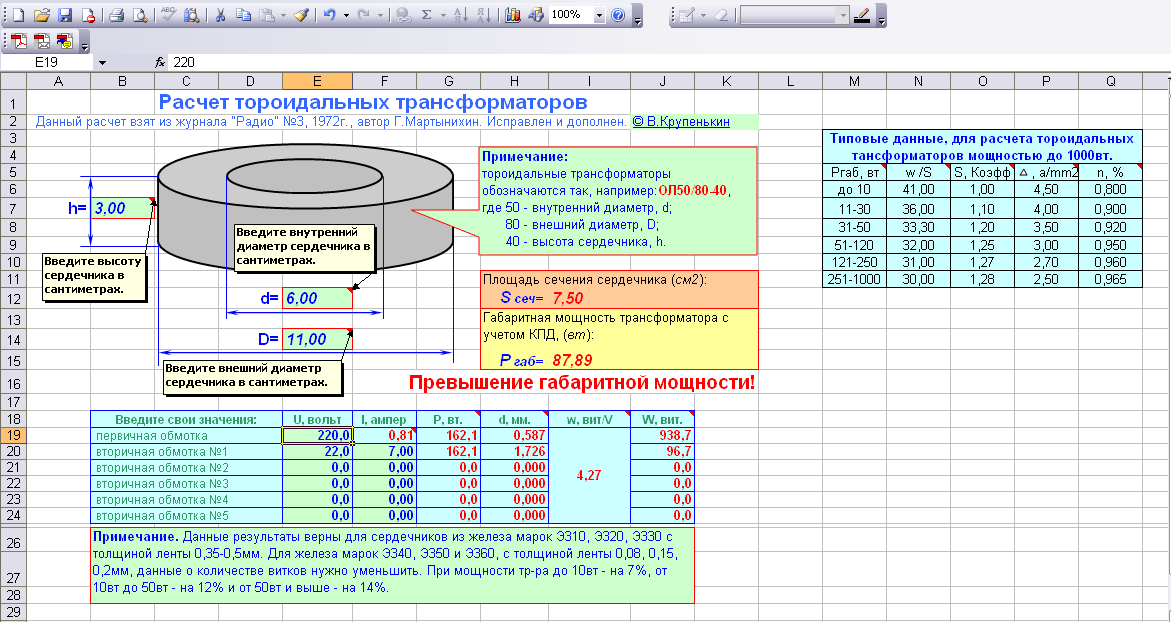 Уникальные эксплуатационные характеристики высоко ценятся как в бытовых, так и промышленных сферах. Помимо этого, тороидальный агрегат имеет ряд дополнительных преимуществ в отличие от стандартных стержневых и бронированных моделей:
Уникальные эксплуатационные характеристики высоко ценятся как в бытовых, так и промышленных сферах. Помимо этого, тороидальный агрегат имеет ряд дополнительных преимуществ в отличие от стандартных стержневых и бронированных моделей:
- У мастеров появилась отличная возможность использовать для сердечника сталь с повышенной магнитной проницаемостью (Э-370, 340).
- Известно, что итоговый поток рассеяния в идеальной тороидальной катушке должен быть равен нулю. В таком трансформаторе этот показатель имеет некоторую конечную величину. Но такие потоки рассеяния не такие уж и большие, как у обычных моделей, поэтому внешние магнитные поля не влияют на слаженную работу трансформатора.
- В сердечнике полностью отсутствуют зазоры и стыки.
- Мастер может смело использовать структурные свойства сердечника, так как в тороидальном агрегате направление магнитного поля полностью совпадает с прокатом ленты.
Все вышеперечисленные преимущества позволяют добиться высоких экономических и электрических показателей.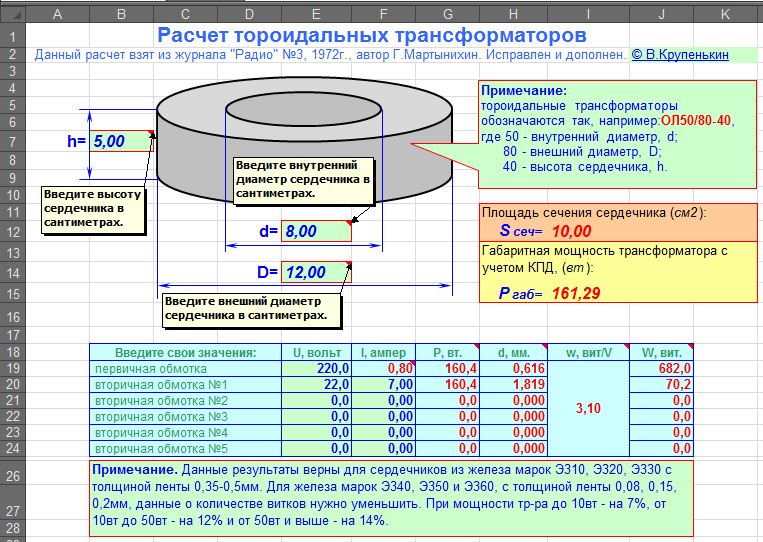 За счёт этого существенно возрастает производительность оборудования:
За счёт этого существенно возрастает производительность оборудования:
- Существенно уменьшается общее количество витков, которые используются для получения величины индуктивной первичной обмотки. Такой эффект достигается благодаря использованию сталей с высокой магнитной проницаемостью. В отдельных конструкциях мастерам удалось снизить итоговый расход меди на 25%.
- Полное отсутствие зазоров и наличие высоколегированной стали является причиной того, что в сердечнике трансформатора достигается более высокая индукция. Это функциональное преимущество совершенно не влияет на коэффициент нелинейных искажений. В результате мастеру удаётся повысить Bmax в два раза, что считается невозможным в броневых трансформаторах. В итоге снижается итоговый вес и объём рабочего сердечника.
- Равномерная частотная характеристика каскад достигается за счёт небольшой величины индуктивности рассеяния. Наличие минимальных искажений по вине переходных процессов позволяет использовать довольно глубокую обратную связь отрицательного типа.

В связи с тем, что тороидальный трансформатор обладает небольшим магнитным полем, даже самый тесный монтаж не влияет на взаимодействие с другими элементами конструкции.
Самостоятельное изготовление агрегата
Прежде чем приступить к созданию такого агрегата, необходимо подготовить все необходимые инструменты и материалы. Для изготовления более качественной модели может понадобиться даже швейная машинка, прочная игла и обычные спички, но такие детали можно найти практически в каждом доме.
Основным расходным материалом является железо, из него изготавливаются базовые части трансформатора. Для работы понадобится качественная сталь, которая должна быть в форме тора. Не стоит забывать и о хорошем проводе в лаковой изоляции. Надёжная фиксация не может обойтись без клея ПВА и малярного скотча.
Отдельно стоит учесть, что качественная работа обмоток зависит от изоленты на тканевой основе.
А также стоит приобрести высококачественный провод в резиновой или силиконовой изоляции. Этот элемент понадобится для надёжного соединения всех концов обмотки.
Подготовка трансформаторной стали
Начинающим мастерам может показаться, что достать базовый элемент конструкции крайне сложно, но на практике всё обстоит совершенно иначе. Дело в том, что даже обычные пункты приёма металла часто располагают неработоспособными стабилизаторами напряжения. В советский период они были очень распространены, так как использовались в чёрно-белых телевизорах, что продлевало работоспособность кинескопов.
Исправность такого устройства совершенно не имеет значения, так как особой ценностью обладают только тороидальные трансформаторы, которые расположены во внутреннем отсеке стабилизатора. Именно эта часть используется мастерами в качестве основы всей конструкции.
На пути к изъятию трансформаторов всегда лежит обмотка, изготовленная из алюминиевого провода. Не стоит забывать о том, что сердечник тоже нуждается в подготовительных работах.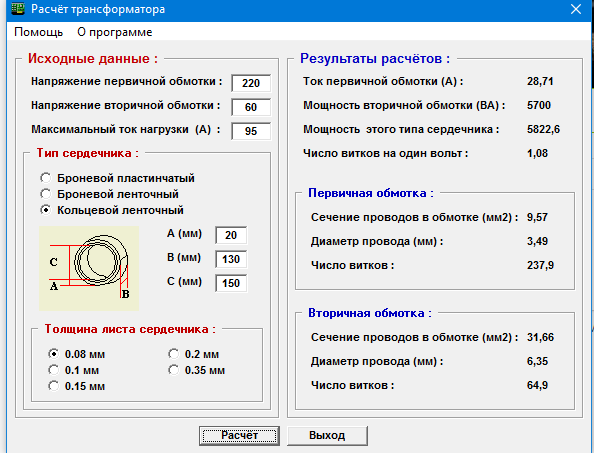 Мастер должен максимально округлить острые края этой детали, так как в процессе намотки может повредиться лаковая изоляция. Поверх трансформаторной стали обязательно укладывается изолента на тканевой основе. В этом случае нужен всего один изоляционный слой.
Мастер должен максимально округлить острые края этой детали, так как в процессе намотки может повредиться лаковая изоляция. Поверх трансформаторной стали обязательно укладывается изолента на тканевой основе. В этом случае нужен всего один изоляционный слой.
Правила обмотки
Прежде чем приступить к этому виду работы, нужно сделать расчёт тороидального трансформатора по сечению сердечника. Конечно, мастер может использовать специальные онлайн-калькуляторы, которых на просторах интернета существует очень много. Но можно выбрать более простой вариант, где для всех вычислений нужно подготовить только линейку и калькулятор.
Конечно, он может иметь некоторые погрешности, так как расчёт не подразумевает соблюдения всех тех факторов, которые встречаются в природе. Главное, придерживаться правила о том, что итоговая мощность во вторичной катушке не должна превышать аналогичных показателей в первой обмотке.
Когда мастер дошёл до этого этапа и нужно сделать намотку тороидального агрегата, ему стоит быть крайне внимательным, так как этот процесс довольно трудоёмкий. Отличным считается тот вариант, когда есть возможность самостоятельно разобрать магнитопровод, а уже после намотки собрать его.
В противном случае можно прибегнуть к помощи обычного веретена, на которое нужно аккуратно намотать определённое количество заранее подготовленного провода. Только после этого веретено можно пропустить необходимое количество раз сквозь тор, равномерно укладывая витки обмоток. Конечно, на реализацию такой идеи уйдёт достаточно много времени, но результат того стоит.
Стоит отметить, что в стандартных ситуациях мастера проводят дополнительную изоляцию тороидального сердечника от обмоток (даже в том случае, если используется лакированная проволока). Особой популярностью пользуется высококачественный электротехнический картон, который соответствует всем стандартам ГОСТ 2824 .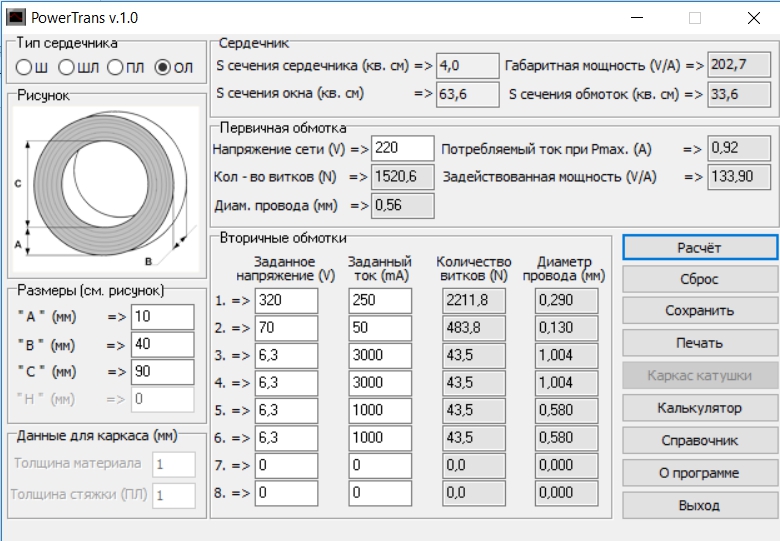 Толщина этого материала находится в пределах 0,8 мм.
Толщина этого материала находится в пределах 0,8 мм.
Во время работы мастера придерживаются следующей схемы:
- Картон аккуратно наматывается на сердечник с небольшим захватом предыдущего витка. Конец материала обязательно фиксируется киперной лентой либо клеем ПВА.
- Все торцы сердечника должны быть защищены картонными шайбами с небольшими надрезами от 10 до 20 мм, длина шага — 35 мм. Как наружная, так и внутренняя грань обязательно закрывается небольшими полосами. Стоит отметить, что технологические шайбы фиксируются на финишном этапе, а все прорезиненные зубцы загибаются. Поверх всей конструкции наматывается киперная лента.
- Если надрезы были сделаны на самых полосах, тогда должен присутствовать небольшой запас, чтобы добиться большей высоты торца. Все кольца должны быть прикреплены строго по ширине, накладываются они поверх загибов.
- В редких случаях кольца могут быть изготовлены из специальной электротехнической фанеры, толстого текстолита.
 Уязвимую внутреннюю и внешнюю грань защищают картонными полосами с небольшими загибами по краям. Между первыми витками обмотки и сердечником должен присутствовать небольшой воздушный зазор. Такой подход особенно важен в тех случаях, когда края под проволокой протрутся. Так уязвимая токонесущая часть никогда не коснётся тороидального сердечника. На верхний слой обязательно наматывается киперная лента. В некоторых случаях мастера предпочитают сглаживать внешнее ребро колец, за счёт чего намотка углов идёт плавно.
Уязвимую внутреннюю и внешнюю грань защищают картонными полосами с небольшими загибами по краям. Между первыми витками обмотки и сердечником должен присутствовать небольшой воздушный зазор. Такой подход особенно важен в тех случаях, когда края под проволокой протрутся. Так уязвимая токонесущая часть никогда не коснётся тороидального сердечника. На верхний слой обязательно наматывается киперная лента. В некоторых случаях мастера предпочитают сглаживать внешнее ребро колец, за счёт чего намотка углов идёт плавно.
Если трансформатор обладает повышенной мощностью, тогда медный провод должен быть прямоугольного сечения. Такой подход позволяет сэкономить свободное пространство. Жила обязательно должна быть толстой, чтобы она не плавилась во время того, как по ней проходит большое напряжение.
Тонкости расчётных манипуляций
Чаще всего первичная обмотка питается от обычной сети переменного напряжения в 220 В. Если мастеру нужно две вторичные обмотки, чтобы каждая выдавала минимум по 12 В, то площадь сечения должна составлять минимум 0,23 кв. мм. Но этих данных мало, чтобы правильно рассчитать тороидальный трансформатор.
Если мастеру нужно две вторичные обмотки, чтобы каждая выдавала минимум по 12 В, то площадь сечения должна составлять минимум 0,23 кв. мм. Но этих данных мало, чтобы правильно рассчитать тороидальный трансформатор.
Мастеру нужно разделить 220 В на определённую сумму напряжений вторичной цепи. Так можно получить коэффициент 3,9, который будет обозначать, что сечение провода для вторичной обмотки должно быть аналогичным с этим показателем. А вот для того, чтобы определить количество витков, нужно прибегнуть к достаточно простой формуле: напряжение 220 В умножить на коэффициент 40, а полученную цифру следует разделить на площадь поперечного сечения магнитопровода.
Отдельно стоит учесть, что от правильности проведённых расчётов зависит уровень КПД тороидального трансформатора и его эксплуатационный срок. Именно поэтому лучше несколько раз всё перепроверить, дабы не допустить самых распространённых ошибок.
Рекомендации специалистов
Когда мастер тщательным образом изучил способ изготовления трансформатора своими руками, он может смело приступать к практической части. Так как намотка витков считается очень сложным процессом, понадобится запастись терпением, чтобы итоговый результат оправдал все ожидания. Ведь именно от того, насколько качественно выполнен этот этап, зависят эксплуатационные характеристики устройства.
Так как намотка витков считается очень сложным процессом, понадобится запастись терпением, чтобы итоговый результат оправдал все ожидания. Ведь именно от того, насколько качественно выполнен этот этап, зависят эксплуатационные характеристики устройства.
Для упрощения этой задачи можно использовать специальный станок, предназначенный для намотки тороидальных трансформаторов. Цена такого агрегата считается доступной, а при желании его можно изготовить и своими руками.
онлайн-калькуляторы, особенности автотрансформаторов и торов
Одним из часто применяемых устройств в областях энергетики, электроники и радиотехники является трансформатор. Часто от его параметров зависит надёжность работы приборы в целом. Случается так, что при выходе трансформатора из строя или при самостоятельном изготовлении радиоприборов не получается найти устройство с нужными параметрами серийного производства. Поэтому приходится выполнять расчёт трансформатора и его изготовление самостоятельно.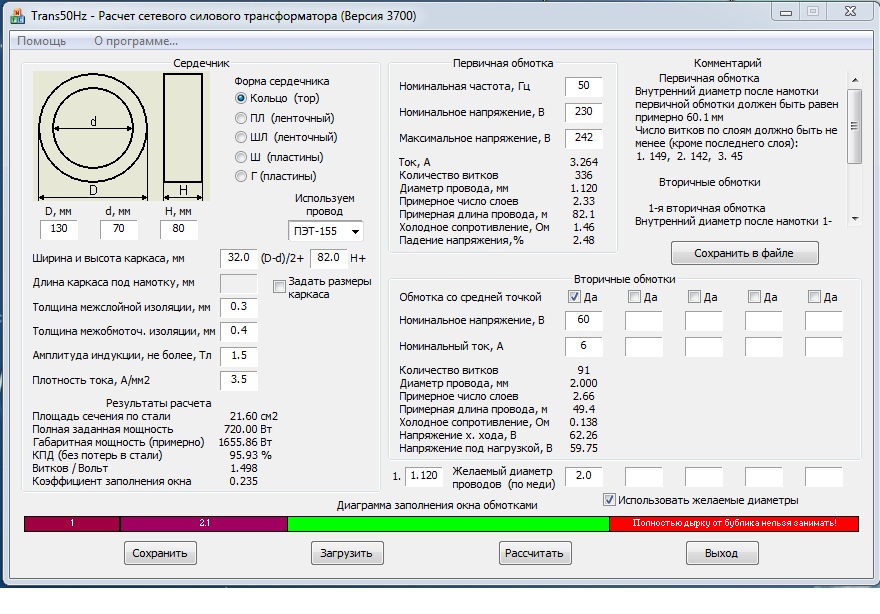
Принцип работы устройства
Трансформатор — это электротехническое устройство, предназначенное для передачи энергии без изменения её формы и частоты. Используя в своей работе явление электромагнитной индукции, устройство применяется для преобразования переменного сигнала или создания гальванической развязки. Каждый трансформатор собирается из следующих конструктивных элементов:
- сердечника;
- обмотки;
- каркаса для расположения обмоток;
- изолятора;
- дополнительных элементов, обеспечивающих жёсткость устройства.
В основе принципа действия любого трансформаторного устройства лежит эффект возникновения магнитного поля вокруг проводника с текущим по нему электрическим током. Такое поле также возникает вокруг магнитов. Током называется направленный поток электронов или ионов (зарядов). Взяв проволочный проводник и намотав его на катушку и подключив к его концам прибор для измерения потенциала можно наблюдать всплеск амплитуды напряжения при помещении катушки в магнитное поле. Это говорит о том, что при воздействии магнитного поля на катушку с намотанным проводником получается источник энергии или её преобразователь.
Это говорит о том, что при воздействии магнитного поля на катушку с намотанным проводником получается источник энергии или её преобразователь.
В устройстве трансформатора такая катушка называется первичной или сетевой. Она предназначена для создания магнитного поля. Стоит отметить, что такое поле обязательно должно всё время изменяться по направлению и величине, то есть быть переменным.
Классический трансформатор состоит из двух катушек и магнитопровода, соединяющего их. При подаче переменного сигнала на контакты первичной катушки возникающий магнитный поток через магнитопровод (сердечник) передаётся на вторую катушку. Таким образом, катушки связаны силовыми магнитными линиями. Согласно правилу электромагнитной индукции при изменении магнитного поля в катушке индуктируется переменная электродвижущая сила (ЭДС). Поэтому в первичной катушки возникает ЭДС самоиндукции, а во вторичной ЭДС взаимоиндукции.
Количество витков на обмотках определяет амплитуду сигнала, а диаметр провода наибольшую силу тока. При равенстве витков на катушках уровень входного сигнала будет равен выходному. В случае когда вторичная катушка имеет в три раза больше витков, амплитуда выходного сигнала будет в три раза больше, чем входного — и наоборот.
От сечения провода, используемого в трансформаторе, зависит нагрев всего устройства. Правильно подобрать сечение возможно, воспользовавшись специальными таблицами из справочников, но проще использовать трансформаторный онлайн-калькулятор.
Отношение общего магнитного потока к потоку одной катушки устанавливает силу магнитной связи. Для её увеличения обмотки катушек размещаются на замкнутом магнитопроводе. Изготавливается он из материалов имеющих хорошую электромагнитную проводимость, например, феррит, альсифер, карбонильное железо. Таким образом, в трансформаторе возникают три цепи: электрическая — образуемая протеканием тока в первичной катушке, электромагнитная — образующая магнитный поток, и вторая электрическая — связанная с появлением тока во вторичной катушке при подключении к ней нагрузки.
Правильная работа трансформатора зависит и от частоты сигнала. Чем она больше, тем меньше возникает потерь во время передачи энергии. А это означает, что от её значения зависят размеры магнитопровода: чем частота больше, тем размеры устройства меньше. На этом принципе и построены импульсные преобразователи, изготовление которых связано с трудностями разработки, поэтому часто используется калькулятор для расчёта трансформатора по сечению сердечника, помогающий избавиться от ошибок ручного расчёта.
Виды сердечников
Трансформаторы отличаются между собой не только сферой применения, техническими характеристиками и размерам, но и типом магнитопровода. Очень важным параметром, влияющим на величину магнитного поля, кроме отношения витков, является размер сердечника. От его значения зависит способность насыщения. Эффект насыщения наступает тогда, когда при увеличении тока в катушке величина магнитного потока остаётся неизменной, т. е. мощность не изменяется.
е. мощность не изменяется.
Для предотвращения возникновения эффекта насыщения понадобится правильно рассчитать объём и сечение сердечника, от размеров которого зависит мощность трансформатора. Следовательно, чем больше мощность трансформатора, тем большим должен быть его сердечник.
По конструкции сердечник разделяют на три основных вида:
- стержневой;
- броневой;
- тороидальный.
Стержневой магнитопровод представляет собой П-образный или Ш-образный вид конструкции. Собирается из стержней, стягивающихся ярмом. Для защиты катушек от влияния внешних электромагнитных сил используются броневые магнитопроводы. Их ярмо располагается на внешней стороне и закрывает стержень с катушкой. Тороидальный вид изготавливается из металлических лент. Такие сердечники из-за своей кольцевой конструкции экономически наиболее выгодны.
Зная форму сердечника, несложно рассчитать мощность трансформатора. Находится она по несложной формуле: P=(S/K)*(S/K), где:
- S — площадь сечения сердечника.

- K — постоянный коэффициент равный 1,33.
Площадь сердечника находится в зависимости от его вида, её единица измерения — сантиметр в квадрате. Полученный результат измеряется в ваттах. Но на практике часто приходится выполнять расчёт сечения сердечника по необходимой мощности трансформатора: Sс = 1.2√P, см2. Исходя из формул можно подтвердить вывод: что чем больше мощность изделия, тем габаритней используется сердечник.
Типовой расчёт параметров
Довольно часто радиолюбители используют при расчёте трансформатора упрощённую методику. Она позволяет выполнить расчёт в домашних условиях без использования величин, которые трудно узнать. Но проще использовать готовый для расчёта трансформатора онлайн-калькулятор. Для того чтобы воспользоваться таким калькулятором, понадобится знать некоторые данные, а именно:
- напряжение первичной и вторичной обмотки;
- габаритны сердечника;
- толщину пластины.
После их ввода понадобится нажать кнопку «Рассчитать» или похожую по названию и дождаться результата.
Стержневой тип магнитопровода
В случае отсутствия возможности расчёта на калькуляторе выполнить такую операцию самостоятельно несложно и вручную. Для этого потребуется определиться с напряжением на выходе вторичной обмотки U2 и требуемой мощностью Po. Расчёт происходит следующим образом:
- Рассчитывается ток нагрузки: In=Po/U2, А.
- Вычисляется величина тока вторичной обмотки: I2 = 1,5*In, А.
- Определяется мощность вторичной обмотки: P2 = U2*I2, Вт.
- Находится общая мощность устройства: Pт = 1,25*P2, Вт.
- Вычисляется сила тока первичной обмотки: I1 = Pт/U1, А.
- Находится необходимое сечение магнитопровода: S = 1,3*√ Pт, см².
Следует отметить, что если конструируется устройство с несколькими выводами во вторичной обмотке, то в четвёртом пункте все мощности суммируются, и их результат подставляется вместо P2.
После того как первый этап выполнен, приступают к следующей стадии расчёта. Число витков в первичной обмотке находится по формуле: K1 = 50*U1/S. А число витков вторичной обмотке определяется выражением K2= 55* U2/S, где:
- U1 — напряжение первичной обмотке, В.
- S — площадь сердечника, см².
- K1, K2 — число витков в обмотках, шт.
Остаётся вычислить диаметр наматываемой проволоки. Он равен D = 0,632*√ I, где:
- d — диаметр провода, мм.
- I — обмоточный ток рассчитываемой катушки, А.
При подборе магнитопровода следует соблюдать соотношение 1 к 2 ширины сердечника к его толщине. По окончании расчёта выполняется проверка заполняемости, т. е. поместится ли обмотка на каркас. Для этого площадь окна вычисляется по формуле: Sо = 50*Pт, мм2.
Особенности автотрансформатора
Автотрансформаторы рассчитываются аналогично простым трансформаторам, только сердечник определяется не на всю мощность, а на мощность разницы напряжений.
Например, мощность магнитопровода 250 Вт, на входе 220 вольт, на выходе требуется получить 240 вольт. Разница напряжений составляет 20 В, при мощности 250 Вт ток будет равен 12,5 А. Такое значение тока соответствует мощности 12,5*240=3000 Вт. Потребление сетевого тока составляет 12,5+250/220=13,64А, что как раз и соответствует 3000Вт=220В*13,64А. Трансформатор имеет одну обмотку на 240 В с отводом на 220 В, который подключён к сети. Участок между отводом и выходом мотается проводом, рассчитанным на 12,5А.
Таким образом, автотрансформатор позволяет получить на выходе мощность значительно больше, чем трансформатор на таком же сердечнике при небольшом коэффициенте передачи.
Трансформатор тороидального типа
Тороидальные трансформаторы имеют ряд преимуществ по сравнению с другими типами: меньший размер, меньший вес и при этом большее КПД.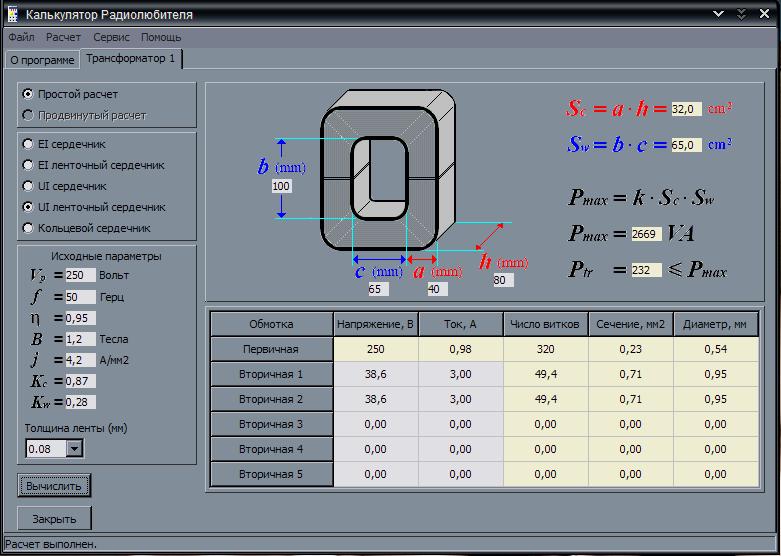 При этом они легко наматываются и перематываются. Использование онлайн-калькулятора для расчёта тороидального трансформатора позволяет не только сократить время изготовления изделия, но и «на лету» поэкспериментировать с разными вводными данными. В качестве таких данных используются:
При этом они легко наматываются и перематываются. Использование онлайн-калькулятора для расчёта тороидального трансформатора позволяет не только сократить время изготовления изделия, но и «на лету» поэкспериментировать с разными вводными данными. В качестве таких данных используются:
- напряжение входной обмотки, В;
- напряжение выходной обмотки, В;
- ток выходной обмотки, А;
- наружный диаметр тора, мм;
- внутренний диаметр тора, мм;
- высота тора, мм.
Необходимо отметить, что почти все онлайн-программы не демонстрируют особой точности в случае расчёта импульсных трансформаторов. Для получения высокой точности можно воспользоваться специально разработанными программами, например, Lite-CalcIT, или рассчитать вручную. Для самостоятельного расчёта используются следующие формулы:
- Мощность выходной обмотки: P2=I2*U2, Вт.
- Габаритная мощность: Pg=P2/Q, Вт. Где Q — коэффициент, берущийся из справочника (0,76−0,96).

- Фактическое сечение «железа» в месте размещения катушки: Sch= ((D-d)*h)/2, мм2.
- Расчётное сечение «железа» в месте расположения катушки: Sw =√Pq/1.2, мм2
- Площадь окна тора: Sfh=d*s* π/4, мм2.
- Значение рабочего тока входной обмотки: I1=P2/(U1*Q*cosφ), А, где cosφ справочная величина (от 0,85 до 0,94).
- Сечение провода находится отдельно для каждой обмотки из выражения: Sp = I/J, мм2., где J- плотность тока, берущаяся из справочника (от 3 до 5).
- Число витков в обмотках рассчитывается отдельно для каждой катушки: Wn=45*Un*(1-Y/100)/Bm* Sch шт., где Y — табличное значение, которое зависит от суммарной мощности выходных обмоток.
- Остается найти выходную мощность и расчёт тороидального силового трансформатора считается выполненным. Pout = Bm*J*Kok*Kct* Sch* Sfh /0,901, где: Bm — магнитная индукция, Kok — коэффициент заполнения проводом, Kct —коэффициент заполнения железом.
Все значения коэффициентов берутся из справочника радиоаппаратуры (РЭА).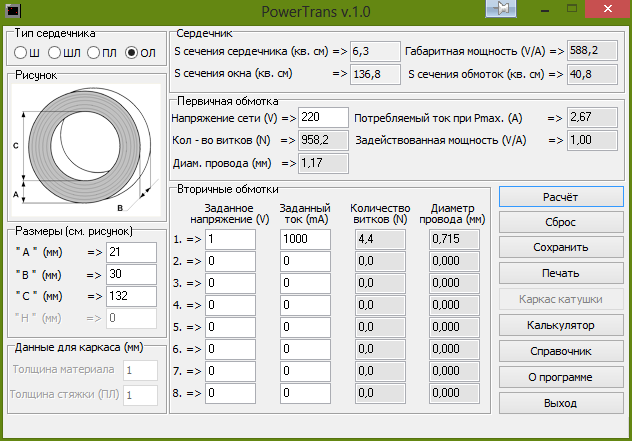 Таким образом, проводить вычисления в ручном режиме несложно, но потребуется аккуратность и доступ к справочным данным, поэтому гораздо проще использовать онлайн-сервисы.
Таким образом, проводить вычисления в ручном режиме несложно, но потребуется аккуратность и доступ к справочным данным, поэтому гораздо проще использовать онлайн-сервисы.
Рекомендации по сборке и намотке
При сборке трансформатора своими руками пластины сердечника собираются «вперекрышку». Магнитопровод стягивается обоймой или шпилечными гайками. Для того чтобы не нарушить изоляцию, шпильки закрываются диэлектриком. Стягивать «железо» нужно с усилием: если его окажется недостаточно при работе устройства возникнет гул.
Проводники наматываются на катушку плотно и равномерно, каждый последующий ряд изолируется от предыдущего тонкой бумагой или лавсановой плёнкой. Последний ряд обматывается киперной лентой или лакотканью. Если в процессе намотки выполняется отвод, то провод разрывается, а на место разрыва впаивается отвод. Это место тщательно изолируется. Закрепляются концы обмоток с помощью ниток, которыми привязываются провода к поверхности сердечника.
При этом существует хитрость: после первичной обмотки не следует наматывать всю вторичную обмотку сразу.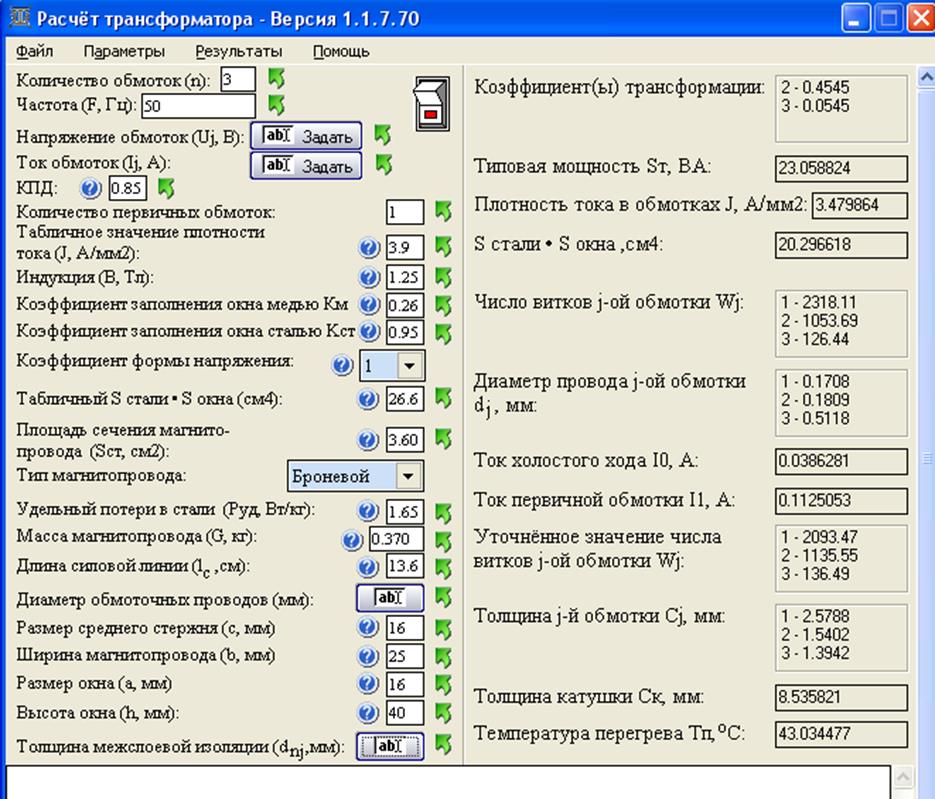 Намотав 10—20 витков, нужно измерить величину напряжения на её концах.
Намотав 10—20 витков, нужно измерить величину напряжения на её концах.
По полученному значению можно представить, сколько витков потребуется для получения нужной амплитуды выходного напряжения, тем самым контролируя полученный расчёт при сборке трансформатора.
Онлайн расчет трансформатора за 6 простых шагов
Ремонт современных электрических приборов и изготовление самодельных конструкций часто связаны с блоками питания, пускозарядными и другими устройствами, использующими трансформаторное преобразование энергии. Их состояние надо уметь анализировать и оценивать.
Считаю, что вам поможет выполнить расчет трансформатора онлайн калькулятор, работающий по подготовленному алгоритму, или старый проверенный дедовский метод с формулами, требующий вдумчивого отношения. Испытайте оба способа, используйте лучший.
Содержание статьи
Сразу заостряю ваше внимание на том вопросе, что приводимые методики не способны точно учесть магнитные свойства сердечника, который может быть выполнен из разных сортов электротехнических стали.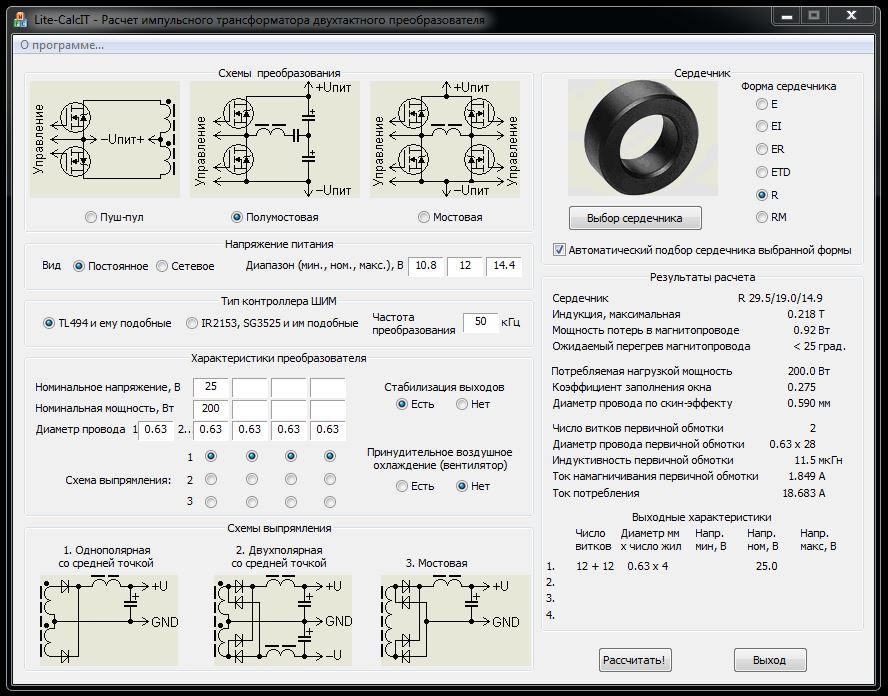
Поэтому реальные электрические характеристики собранного трансформатора могут отличаться на сколько-то вольт или число ампер от полученного расчетного значения. На практике это обычно не критично, но, всегда может быть откорректировано изменением числа количества в одной из обмоток.
Поперечное сечение магнитопровода передает первичную энергию магнитным потоком во вторичную обмотку. Обладая определенным магнитным сопротивлением, оно ограничивает процесс трансформации.
От формы, материала и сечения сердечника зависит мощность, которую можно преобразовывать и нормально передавать во вторичную цепь.
Как пользоваться онлайн калькулятором для расчета трансформатора пошагово
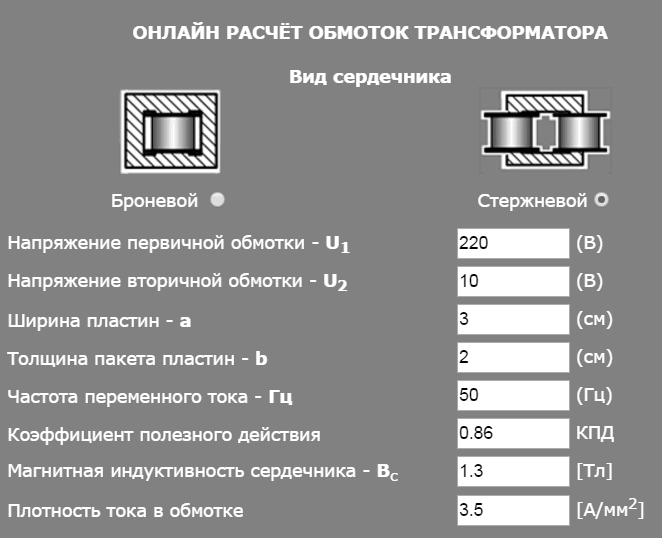
Подготовка исходных данных за 6 простых шагов
Шаг №1. Указание формы сердечника и его поперечного сечения
Лучшим распределением магнитного потока обладают сердечники, набранные из Ш-образных пластин. Кольцевая форма из П-образных составляющих деталей обладает большим сопротивлением.
Для проведения расчета надо указать форму сердечника по виду пластины (кликом по точке) и его измеренные линейные размеры:
- Ширину пластины под катушкой с обмоткой.
- Толщину набранного пакета.
Вставьте эти данные в соответствующие ячейки таблицы.
Шаг №2. Выбор напряжений
Трансформатор создается как повышающей, понижающей (что в принципе обратимо) или разделительной конструкцией. В любом случае вам необходимо указать, какие напряжения вам нужны на его первичной и вторичной обмотке в вольтах.
Заполните указанные ячейки.
Шаг №3. Частота сигнала переменного тока
По умолчанию выставлена стандартная величина бытовой сети 50 герц. При необходимости ее нужно изменить на требуемую по другому расчету. Но, для высокочастотных трансформаторов, используемых в импульсных блоках питания, эта методика не предназначена.
Их создают из других материалов сердечника и рассчитывают иными способами.
Шаг №4. Коэффициент полезного действия
У обычных моделей сухих трансформаторов КПД зависит от приложенной электрической мощности и вычисляется усредненным значением.
Но, вы можете откорректировать его значение вручную.
Шаг №5. Магнитная индуктивность
Параметр определяет зависимость магнитного потока от геометрических размеров и формы проводника, по которому протекает ток.
По умолчанию для расчета трансформаторов принят усредненный параметр в 1,3 тесла. Его можно корректировать.
Шаг №6. Плотность тока
Термин используется для выбора провода обмотки по условиям эксплуатации. Среднее значение для меди принято 3,5 ампера на квадратный миллиметр поперечного сечения.
Для работы трансформатора в условиях повышенного нагрева его следует уменьшить. При принудительном охлаждении или пониженных нагрузках допустимо увеличить. Однако 3,5 А/мм кв вполне подходит для бытовых устройств.
Выполнение онлайн расчета трансформатора
После заполнения ячеек с исходными данными нажимаете на кнопку «Рассчитать». Программа автоматически обрабатывает введенные данные и показывает результаты расчета таблицей.
Как рассчитать силовой трансформатор по формулам за 5 этапов
Привожу упрощенную методику, которой пользуюсь уже несколько десятков лет для создания и проверки самодельных трансформаторных устройств из железа неизвестной марки по мощности нагрузки.
По ней мне практически всегда получалось намотать схему с первой попытки. Очень редко приходилось добавлять или уменьшать некоторое количество витков.
Этап №1. Как мощность сухого трансформатора влияет на форму и поперечное сечение магнитопровода
В основу расчета положено среднее соотношение коэффициента полезного действия ŋ, как отношение электрической мощности S2, преобразованной во вторичной обмотке к приложенной полной S1 в первичной.
ŋ = S1 / S2
Потери мощности во вторичной обмотке оценивают по статистической таблице.
| Мощность трансформатора, ватты | Коэффициент полезного действия ŋ |
| 15÷50 | 0,50÷0,80 |
| 50÷150 | 0,80÷0,90 |
| 150÷300 | 0,90÷0,93 |
| 300÷1000 | 0,93÷0,95 |
| >1000 | 0.95÷0,98 |
Электрическая мощность устройства определяется произведением номинального тока, протекающего по первичной обмотке в амперах, на напряжение бытовой проводки в вольтах.
Она преобразуется в магнитную энергию, протекающую по сердечнику, полноценно распределяясь в нем в зависимости от формы распределения потоков:
- для кольцевой фигуры из П-образных пластин площадь поперечного сечения под катушкой магнитопровода рассчитывается как Qc=√S1;
- у сердечника из Ш-образных пластин Qc=0,7√S1.
Таким образом, первый этап расчета позволяет: зная необходимую величину первичной или вторичной мощности подобрать магнитопровод по форме и поперечному сечению сердечника;или по габаритам имеющегося магнитопровода оценить электрические мощности, которые сможет пропускать проектируемый трансформатор.
Этап №2. Особенности вычисления коэффициента трансформации и токов внутри обмоток
Силовой трансформатор создается для преобразования электрической энергии одной величины напряжения в другое, например, U1=220 вольт на входе и U2=24 V — на выходе.
Коэффициент трансформации в приведенном примере записывается как выражение 220/24 или дробь с первичной величиной напряжения в числителе, а вторичной — знаменателе. Он же позволяет определить соотношение числа витков между обмотками.
n = W1 / W2
На первом этапе мы уже определили электрические мощности каждой обмотки. По ним и величине напряжения необходимо рассчитать силу электрического тока I=S/U внутри любой катушки.
Этап №3. Как вычислить диаметры медного провода для каждой обмотки
При определении поперечного сечения проводника катушки используется эмпирическое выражение, учитывающее, что плотность тока лежит в пределах 1,8÷3 ампера на квадратный миллиметр.
Величину тока в амперах для каждой обмотки мы определили на предыдущем шаге.
Теперь просто извлекаем из нее квадратный корень и умножаем на коэффициент 0,8. Полученное число записываем в миллиметрах. Это расчетный диаметр провода для катушки.
Он подобран с учетом выделения допустимого тепла из-за протекающего по нему тока. Если место в окне сердечника позволяет, то диаметр можно немного увеличить. Тогда эти обмотки будут лучше приспособлены к тепловым нагрузкам.
Когда даже при плотной намотке все витки провода не вмещаются в окне магнитопровода, то его поперечное сечение допустимо чуть уменьшить. Но, такой трансформатор следует использовать для кратковременной работы и последующего охлаждения.
При выборе диаметра провода добиваются оптимального соотношения между его нагревом при эксплуатации и габаритами свободного пространства внутри сердечника, позволяющими разместить все обмотки.
Этап №4. Определение числа витков обмоток по характеристикам электротехнической стали: важные моменты
Вычисление основано на использовании магнитных свойств железа сердечника. Промышленные трансформаторы собираются из разных сортов электротехнической стали, подбираемые под конкретные условия работы. Они рассчитываются по сложным, индивидуальным алгоритмам.
Домашнему мастеру достаются магнитопроводы неизвестной марки, определить электротехнические характеристики которой ему практически не реально. Поэтому формулы учитывают усредненные параметры, которые не сложно откорректировать при наладке.
Для расчета вводится эмпирический коэффициент ω’. Он учитывает величину напряжения в вольтах, которое наводится в одном витке катушки и связан с поперечным сечением магнитопровода Qc (см кв).
ω’=45/Qc (виток/вольт)
В первичной обмотке число витков вычислим, как W1= ω’∙U1, а во вторичной — W2= ω’∙U2.
Этап №5. Учет свободного места внутри окна магнитопровода
На этом шаге требуется прикинуть: войдут ли все обмотки в свободное пространство окна сердечника с учетом габаритов катушки.
Для этого допускаем, что провод имеет сечение не круглое, а квадрата со стороной одного диаметра. Тогда при совершенно идеальной плотной укладке он займет площадь, равную произведению единичного сечения на количество витков.
Увеличиваем эту площадь процентов на 30, ибо так идеально намотать витки не получится. Это будет место внутри полостей катушки, а она еще займет определенное пространство.
Далее сравниваем полученные площади для катушек каждой обмотки с окном магнитопровода и делаем выводы.
Второй способ оценки — мотать витки «на удачу». Им можно пользоваться, если новая конструкция перематывается проводом со старых рабочих катушек на том же сердечнике.
4 практических совета по наладке и сборке трансформатора: личный опыт
Сборка магнитопровода
Степень сжатия пластин влияет на шумы, издаваемые железом сердечника при вибрациях от протекающего по нему магнитного потока.
Одновременно не плотное прилегание железа с воздушными зазорами увеличивает магнитное сопротивление, вызывает дополнительные потери энергии.
Если для стягивания пластин используются металлические шпильки, то их надо изолировать от железа сердечника бумажными вставками и картонными шайбами.
Иначе по этому креплению возникнет искусственно созданный короткозамкнутый виток. В нем станет наводиться дополнительная ЭДС, значительно снижающая коэффициент полезного действия.
Состояние изоляции крепежных болтов относительно железа сердечника проверяют мегаомметром с напряжением от 1000 вольт. Показание должно быть не менее 0,5 Мом.
Расчет провода по плотности тока
Оптимальные размеры трансформатора играют важную роль для устройств, работающих при экстремальных нагрузках.
Для питающей обмотки, подключенной к бытовой проводке лучше выбирать плотность тока из расчета 2 А/мм кв, а для остальных — 2,5.
Способы намотки витков
Быстрая навивка на станке «внавал» занимает повышенный объем и нормально работает при относительно небольших диаметрах провода.
Качественную укладку обеспечивает намотка плотными витками один возле другого с расположением их рядами и прокладкой ровными слоями изоляции из конденсаторной бумаги, лакоткани, других материалов.
Хорошо подходят для создания диэлектрического слоя целлофановые (не из полиэтилена) ленты. Можно резать их от упаковок сигарет. Отлично справляется с задачами слоя изоляции кулинарная пленка для запекания мясных продуктов и выпечек.
Она же придает красивый вид внешнему покрытию катушки, одновременно обеспечивая ее защиту от механических повреждений.
Обмотки сварочных и пускозарядных устройств, работающие в экстремальных условиях с высокими нагрузками, желательно дополнительно пропитывать между рядами слоями силикатного клея (жидкое стекло).
Ему требуется дать время, чтобы засох. После этого наматывают очередной слой, что значительно удлиняет сроки сборки. Зато созданный по такой технологии трансформатор хорошо выдерживает высокие температурные нагрузки без создания межвитковых замыканий.
Как вариант такой защиты работает пропитка рядов провода разогретым воском, но, жидкое стекло обладает лучшей изоляцией.
Когда длины провода не хватает для всей обмотки, то его соединяют. Подключение следует делать не внутри катушки, а снаружи. Это позволит регулировать выходное напряжение и силу тока.
Замер тока на холостом ходу трансформатора
Мощные сварочные аппараты требуют точного подбора объема пластин и количества витков под рабочее напряжение, что взаимосвязано.
Выполнить качественную наладку позволяет замер тока холостого хода при оптимальной величине напряжения на входной обмотке питания.
Его значение должно укладываться в предел 100÷150 миллиампер из расчета на каждые 100 ватт приложенной мощности для трансформаторных изделий длительного включения. Когда используется режим кратковременной работы с частыми остановками, то его можно увеличить до 400÷500 мА.
Выполняя расчет трансформатора онлайн калькулятором или проверку его вычислений дедовскими формулами, вам придется собирать всю конструкцию в железе и проводах. При первых сборках своими руками можно наделать много досадных ошибок.
Чтобы их избежать рекомендую посмотреть видеоролик владельца Юность Ru. Он очень подробно и понятно объясняет технологию сборки и расчета. Под видео расположено много полезных комментариев, с которыми тоже следует ознакомиться.
Если заметите в ролике некоторые моменты, которые немного отличаются от моих рекомендаций, то можете задавать вопросы в комментариях. Обязательно обсудим.
Расчет размещения животных и кормов в ковчеге, построенном праведным Ноахом — читать онлайн | Валентин Свиридов
Всевышний повелевает Ноаху сделать ковчег из дерева гофер, длиной 150 м, шириной 25 м и высотой 15 м. Ковчег должен иметь ячеистый скелет «с отделениями сделай ковчег»
Взгляд со стороны
Даже те, кто не брал Хумаш в руки, знают историю о Всемирном потопе и чудесном спасении семьи праведного Ноаха и животных «от всякой твари по паре». Знают и, скорее всего, располагают ее в своем сознании «на полке» между легендами викингов и мифами древней Греции. К сожалению, наша эпоха привила всем нам устойчивую псевдонаучную привычку — высокомерно и презрительно относиться к информации, имеющейся в древних источниках, сформированных до эпохи научно-технической революции. Разумеется, не разобравшись.
Может, попробуем разобраться?
Начнем с того, что определим, кого будем спасать. Всех подряд — невозможно и бессмысленно — в мире существует около пяти с половиной тысяч видов млекопитающих, отличающихся друг от друга незначительными признаками. По классификации более общей ступенью является «род». В Торе сказано, что животные, подлежащие спасению, принимались на борт ковчега «по роду их». Классификацию животных много столетий позже предложил Карл Линней в 18 веке, но у нас нет никаких оснований считать, что «род», о котором говорится в Писании, означает что-то другое — например, «семейство» или «вид». Тем более, что понятие «род» больше других подходит в контексте задачи спасения животных — если спасать виды, животных с минимальными различиями, то их количество сильно затрудняет задачу спасения; если «семейства», то размеры ковчега оказываются избыточны, но спасшиеся животные не смогут после спасения в процессе адаптации сформировать то разнообразие животного мира, которое мы наблюдаем сейчас.
Поэтому род — это оптимальная группа по численности и обладающая всеми необходимыми признаками для обеспечения будущего многообразия.
Для того, чтобы осуществить расчет, мы будем опираться на млекопитающих, а насекомых, гадов и птиц условно разместим вместе с животными, поскольку они очень малы и нет смысла высчитывать места в ковчеге для тараканов, ящериц и соек, но примем к расчету дополнительные объемы корма для них. Также, будем иметь в виду, что многие из них питаются переваренным кормом млекопитающих, значит, не требуют дополнительных объемов кормов. А насекомые, активно размножаясь, сами являются кормом для множества животных и птиц.
Рыбы и морские животные к расчету не принимаются, так как ищут спасение своими силами в водах рек и морей.
По современным научным данным количество млекопитающих составляет:
Отряд — 29;
Семейство — 153;
Род — 1229;
Вид — 5500.
Нас интересует род, следовательно, на ковчеге предстоит разместить 1229 пар животных (за вычетом морских).
Всевышний повелевает Ноаху сделать ковчег из дерева гофер, длиной 150 м, шириной 25 м и высотой 15 м. Ковчег должен иметь ячеистый скелет «с отделениями сделай ковчег»), что обеспечит раздельное содержание животных, равномерное распределение веса по палубам (что является критичным во время сильного шторма) и необходимую прочность, чтобы судно не переломилось, находясь на гребне волны. К сожалению, более подробные детали нам не известны. Известно, что ковчег имел четыре палубы: «с нижними, вторыми и третьими (жилищами) сделай его». Почему не три? Потому что, если вы стоите на одном уровне (первом), то требуется, чтобы был «нижний» уровень — под вами и «второе и третье жилище» — т.е. два над вами. Итого — четыре уровня. Как мы увидим далее — это разделение оказалось оптимальным. Ясно, что для очень высоких животных были изготовлены индивидуальные загоны, но таковых — всего три пары — две пары слонов и одна жирафов.
Для удобства расчета мы примем форму ковчега за параллелепипед.
Итак, 150*25*4 = 15 000 кв.м. — это общая площадь ковчега.
Возьмем толщину палуб по 0,4 метра: 150*25*0,4*3 = 4 500 куб.м. — это потери полезного объема.
Теперь вычислим полезный объем ковчега: 3750*15-4500 = 51 750 куб.м.
Следующая задача — распределить животных по размерам, типу питания и определить достаточный размер «каюты». Вначале мы должны сгруппировать животных по размеру и типу питания — в сводной таблице мы видим результат этого распределения, а подробности можно узнать в приложении к тексту:
|
классификация для расчета
|
кол-во родов
|
комментарий
|
|
Не вошли в ковчег
|
30
|
морские животные
|
|
Очень крупные
|
8
|
свыше 1000 кг
|
|
Травоядные крупные
|
27
|
от 100 до 1000 кг
|
|
Плотоядные крупные
|
5
|
от 80 до 500 кг
|
|
Травоядные средние
|
55
|
до 100 кг
|
|
Плотоядные средние
|
18
|
до 80 кг
|
|
Мелкие
|
492
|
до 15 кг
|
|
Очень маленькие
|
594
|
меньше 2-х кг
|
Далее определим размеры ячеек для пары животных, в зависимости от их размера и вычислим совокупную площадь, занятую под размещение животных:
|
РАЗМЕР
|
площадь ячейки на одну пару, кв.м.
|
количество пар зверей
|
ИТОГО
|
|
очень крупный
|
40
|
8
|
320
|
|
травоядный крупный
|
20
|
33
|
660
|
|
плотоядный крупный
|
15
|
5
|
75
|
|
плотоядный средний
|
4
|
18
|
72
|
|
травоядный средний
|
5
|
67
|
335
|
|
маленькие разные
|
1,5
|
492
|
738
|
|
очень маленькие разные
|
0,5
|
594
|
297
|
|
ВСЕГО кв.м.
|
2 497
|
Добавим 10% на проходы, получим 2 747 кв.м. Умножим на высоту палубы, равную 3 метрам, получим объем, равный 8 240 куб.м. Полученные цифры показывают, что операция по спасению животных на ковчеге была вовсе не фантастической, как многим представляется. Все спасаемые животные по роду их заняли площадь менее 20% от полезной площади ковчега.
Но чем же была занята остальная площадь? Животных нужно было чем-то кормить в течение года. Считаем.
Мы взяли нормы кормления животных по минимальным значениям. Это решение обоснованно потому, что животные находились в ковчеге с минимальной активностью и не нуждались в обильных рационах. В качестве корма взяты сено, зерно, сублимированное мясо для плотоядных и сухофрукты для разнообразия рациона. У Ноаха было достаточно времени на заготовки необходимого объема кормов.
|
РАЗМЕР
|
количество пар
|
корма в день на одно животное, кг
|
корма на год, тн
|
вес зверей, тн
|
объем корма, куб.м.
| |
|
очень крупный
|
8
|
130,0
|
759,2
|
32,0
|
15 184,0
|
сено*
|
|
травоядный крупный
|
33
|
18,0
|
433,6
|
39,6
|
8 672,4
|
сено
|
|
плотоядный крупный
|
5
|
5,0
|
18,3
|
2,0
|
1 368,8
|
сублим. мясо**
|
|
средний плотоядный
|
18
|
0,5
|
6,6
|
1,1
|
492,8
|
сублим. мясо
|
|
средний травоядный
|
67
|
5,0
|
244,6
|
8,0
|
4 891,0
|
сено
|
|
маленькие плотоядные
|
246
|
0,3
|
53,9
|
4,4
|
4 040,6
|
сублим. мясо
|
|
маленькие травоядные
|
246
|
1,0
|
179,6
|
4,4
|
3 591,6
|
сено
|
|
очень маленькие травоядные
|
297
|
0,5
|
108,4
|
0,6
|
216,8
|
зерно***
|
|
очень маленькие плотоядные
|
297
|
0,2
|
43,4
|
0,6
|
3 252,2
|
сублим. мясо
|
|
птицы и прочие
|
200,0
|
4
|
400,0
|
зерно
| ||
|
20,0
|
100,0
|
сухофрукты***
| ||||
|
ИТОГО
|
2 067,4
|
96,8
|
42 210,0
| |||
|
* — вес сена в 1 куб.м. = 50 кг
| ||||||
|
** — 1 кг сырого мяса = 1,5 дециметра; сублимированного — 0,75 дециметра
| ||||||
|
*** — в 1 куб.м. 500 кг зерна
| ||||||
|
**** — в 1 куб м. 200 кг сухофруктов
| ||||||
В результате расчетов имеем 42 210 куб метров кормов, заготовленных на год автономного плавания, которые в сумме с «жилыми» объемами составят 50 450 куб метров или 97 % полезного объема ковчега. Оставим 100 кв.м. Ноаху и его семье, а 1200 кв.м. отнесем на компенсацию погрешностей в расчетах.
При расчетном (посчитано с большим запасом) водоизмещении ковчега около 14 тыс тонн, загруженность ковчега составила не более 2,2 тыс тонн, и это обеспечило судну прекрасную плавучесть.
Крупных и средних животных на ковчеге насчитывалось 131 пар, если разделить их для ухода между членами семьи Ноаха, получится 16 пар на человека, плюс 135 мелких, которые требуют существенно меньше усилий по уходу. При шестнадцатичасовом рабочем дне уход за таким количеством зверей работа трудная, но выполнимая.
Тора не рассказывает о технологических подробностях устройства ковчега, но обращает внимание на такую, казалось бы, не значительную деталь — ковчег был осмолен снаружи и изнутри. Снаружи — понятно, а изнутри зачем? Есть предположение, что выделения влаги таким огромным количеством животных могли привести к пропитыванию древесины и значительному снижению плавучести, поэтому и потребовалось осмолить ковчег изнутри.
Согласимся, что наш расчет подробный, но не доскональный. Но любые его уточнения не изменят принципиальную возможность автономного плавания такого количества животных на таком судне в течение года. Что, хотя и не требовалось, но мы постарались показать.
Расчет произведен с использованием данных и количестве родов млекопитающих, приведенных в работе «Систематика современных млекопитающих» Павлинов И.Я. 2003, М.: изд-во МГУ. 297 с.
Поделитесь этой страницей со своими друзьями и близкими:
Одноклассники
Расчет тороидального трансформатора для сварочного полуавтомата
Подбор правильных параметров техники при сварке является очень важным делом. Расчет трансформатора для сварочного полуавтомата имеет ярко выраженную специфику. Здесь могут использоваться как типовые схемы, так и другие варианты, которые подходят по параметрам. Для промышленных трансформаторов можно применять стандартные методики расчета, так как серийно выпускающиеся модели имеют одинаковые параметры, такие как напряжение сварочного трансформатора, тогда как для самодельных изделий такие методы не будут являться действительными. Это касается не только параметров изделия, но и материалов, которые применяются при создании трансформатора. Во втором случае получается намного больше погрешностей, что также следует учитывать. Стандартные методы расчета основаны на методике, которая может определить самое оптимальное значение геометрических и обмоточных параметров трансформатора. Но у данных методик имеются свои недостатки, так как если имеется какой-либо выход за стандартные параметры, то все расчеты могут оказаться недействительными из-за особенностей конструкции и используемых материалов. С учетом современного разнообразия техники, которую можно встретить на рынке для промышленного и частного использования, расчет сварочного трансформатора может оказаться весьма затруднительным.
Трансформатор для сварочного полуавтомата
Ведь не зря, одним из первых дел при расчете является определение количества и вид используемого железа. Таким образом, нужно определить значение наружного и внутреннего диаметра сердечника. Как правило, минимальное значение внутреннего диаметра составляет от 12 см. В некоторых случаях это значение может быть меньше, если обмотка выйдет очень плотной. Проблема здесь может возникнуть при размещении вторичной обмотки, так как в ином случае она может и не поместиться, если диаметр будет меньше предложенного значения. Минимальные рекомендуемые значения имеются и при выборе площади сердечника.
Сварочный трансформатор для сварки полуавтоматом
Стоит отметить, что подавляющее большинство бытовых сварочных аппаратов, куда можно отнести и некоторые модели полуавтоматов, имеют достаточно простую структуру. Они состоят в большинстве случаев из источников переменного тока, что делает их боле дешевыми. Также становится легче ремонт и обслуживание сварочных трансформаторов, если с ними что-то случится. Сама система полуавтомата практически не влияет на принцип действия трансформатора, так как относится к удобству подачи электрода или проволоки. В самых простых моделях используется однофазный трансформатор, который разработан специально для сварки.
На чем базируется расчет сварочного трансформатора
Основными положениями, на которых состоит расчет трансформатора для сварочного полуавтомата сварочного аппарата, являются те, на которых основан принцип его действия. Главным элементом системы является понижающий трансформатор. Этот элемент позволяет изменить стандартное сетевое напряжение 220 В, на пониженное, которое требует холостой ход сварочного трансформатора – 60 В. Ток может регулироваться исходя из вольтамперных характеристик самой системы. Средние характеристики тока для электрода в 3 мм составляет 120 А. Именно в этом случае и оказывается важным расчет сварочного аппарата, ведь когда стержень начинает плавиться при определенном значении силы тока, то он еще и нагревает проволоку обмотки и сердечник трансформатора при определенных значениях. Таким образом, для вычисления оптимальной мощности трансформатора следует узнать рабочее значение, которое можно определить по рабочей силе тока. Для этого применяют формулу U2 = 20+0,04*I2. Здесь:
- U2 – напряжение, которое имеется на вторичной обмотке;
- I2 – максимальный сварочный ток, который может выдать аппарат.
После этого можно перейти к сердечнику. Это центральная часть как простого сварочного аппарата, так и полуавтоматического. Состоит он из металлических пластин. Эти пластины в совокупности могут выдержать определенную нагрузку параметров тока. Данный параметр называется «габаритная мощность». Здесь имеется прямая зависимость от того, какие размеры занимает сердечник. Вычислить габаритную мощность можно зная такие параметры как напряжение холостого хода сварочного трансформатора. Рассчитать все это можно при помощи формулы Uхх = U2S. В данном случае S является площадью сечения вторичной обмотки. Чтобы узнать зависимость площади от диаметра используемого проводника, то следует использовать формулу S = πd2/4.
Также можно просто воспользоваться уже имеющимися готовыми таблицами:
Допустимые нагрузки по току для медных проводов | |||||
Площадь сечения медной жилы, мм2 | Общий диаметр провода с обмоткой, мм | Максимальный ток, А | Площадь сечения медной жилы, мм2 | Общий диаметр провода с обмоткой,мм | Максимальный ток, А |
0.5 | 0.78 | 11 | 35 | 6,7 | 170 |
1,0 | 1,13 | 17 | 70 | 9.5 | 270 |
2,5 | 1,8 | 30 | 120 | 12,4 | 385 |
6.0 | 2,8 | 50 | 185 | 15,4 | 510 |
16 | 4,5 | 100 | 300 | 19,5 | 695 |
Допустимые нагрузки по току для алюминиевых проводов | |||||
Площадь сечения алюминиевой жилы, мм2 | Общий диаметр провода с обмоткой, мм | Максимальный ток, А | Площадь сечения алюминиевой жилы, мм2 | Общий диаметр провода с обмоткой, мм | Максимальный ток, А |
2 | 1,6 | 21 | 35 | 6,7 | 130 |
3 | 1,95 | 27 | 70 | 9.5 | 210 |
5 | 2,52 | 36 | 120 | 12,4 | 295 |
8 | 3,19 | 46 | 185 | 15,4 | 390 |
Далее следует определение такого параметра ка габаритная мощность сердечника. Pгаб = UххI2cos*(φ)/η.Чтобы знать, как рассчитать сварочный трансформатор, требуется использовать ряд формул.Методика расчета с использованием формул
- Здесь φ– является углом смещения фаз между током и напряжением;
- η – коэффициентом полезного действия системы.
При этом следует найти допустимую мощность, с которой бы смог справиться аппарат во время длительной эксплуатации (значение ПР). Данный расчет происходит по следующей формуле Pдл = U2I2 (ПР/100)0.5 * 0.001. В общем, продолжительность беспрерывной эксплуатации и сила тока не связаны между собой. Большее значение на данный параметр оказывает продолжительность дугового режима. Силу одного витка, которая исчисляется в вольтах, можно определить по формуле E=Pдл0.095+0.55.
После этого можно рассчитать наиболее подходящее количество витков для одной обмотки, отдельно для обмоток. Для обоих случаев используются две формулы:
- Для первой обмотки N1= U1/E, здесь U1 – входящее напряжение сети;
- Для второй обмотки N2= U2/E. здесь U2 – входящее напряжение сети.
Исходя из этого, сила тока регулируется изменением расстояния между обмотками, так как с его увеличением теряется и мощность на выходе.
Расчет тороидального трансформатора
Тор является замкнутой поверхностью, в виде которой и выполнен трансформатор тороид. Преимуществом такой формы является высокий коэффициент полезного действия в нем имеется прокладка меж обмоточной изоляции, а меж слоевая отсутствует, так как это невозможно сделать из-за особенностей конструкции. Это делает сборку сердечника более сложной. Чтобы определить габаритную мощность, следует узнать площадь сечения и площадь окна.
Самодельный тороидальный сварочный трансформатор
Площадь окна определяется по формуле Sокна = 3.14*(d2/4). Здесь d является внутренним диаметром тора.
Площадь сечения определяется по формуле Sсеч=h*((D-d)/2). Здесь D является внешним диаметром тора.
Для расчета габаритной мощности применяется самый простой способ умножения полученных результатов, используя формулу Pгаб[Вт] = Sокна[кв.см] * Sсеч[кв.см]. Это предоставляет самые основные параметры расчета, на которых будут основывать все дальнейшие действия. Таким образом, это лишь начало, так как дальше придется использовать дополнительные значения. В дальнейшем, при вычислениях можно ориентироваться на таблицу.
Pгаб | ω1 | ω2 | ∆ (А/мм2) | Η-10 |
менее 10 | 41 | 38 | 4.5 | 8 |
10…30 | 36 | 32 | 4 | 9 |
30…50 | 33.3 | 29 | 3.5 | 9,2 |
50…120 | 32 | 28 | 3 | 9,5 |
Калькулятор самогонщика онлайн: расчет важных параметров
Перед вами несколько простых калькуляторов, рассчитывающих важные для самогоноварения параметры. Эти сервисы будут полезны как опытным, так начинающим винокурам. Они экономят время, избавляя от необходимости делать вычисления вручную.
Калькулятор разбавления спирта водой
Определяет количество воды, которое нужно добавить для получения спирта заданной крепости.
Идет подсчет…
Введите слева исходные данные
Для получения после разбавления,
нужно добавить воды
Калькулятор смешивания двух спиртосодержащих жидкостей
Позволяет рассчитать крепость, объем и вес смеси из двух спиртосодержащих жидкостей при указанной температуре. Калькулятор может использоваться и для расчета параметров разбавления самогона водой, для этого достаточно задать крепость воды равной нулю.
Идет подсчет…
Введите слева исходные данные
Расчет параметров сахарной браги
Калькулятор определяет правильные пропорции браги и максимально возможное содержание спирта в ней после окончания брожения.
Внимание! Учитывайте толерантность (концентрацию спирта в браге, при которой дрожжи погибают) своего штамма дрожжей! Для большинства штаммов этот показатель не превышает 16%.
Идет подсчет…
Введите слева исходные данные
На выходе получится брага с содержанием и удельной плотностью
Потребуется
Замена сахара глюкозой или фруктозой
После брожения из глюкозы или фруктозы получается на 5% меньше спирта, чем из сахарозы, но более высокого качества. Калькулятор рассчитывает, сколько нужно глюкозы, чтобы выход самогона был как с 1 кг сахара.
Идет подсчет…
Введите слева исходные данные
Вам потребуется кг глюкозы (фруктозы)
Спирт в браге до и после брожения
Для рефрактометра со шкалой Brix Wort SG.
Калькулятор рассчитывает, насколько эффективным было брожение (переработали ли дрожжи весь сахар в спирт).
Идет подсчет…
Введите слева исходные данные
На выходе получится сусло с содержанием
Калькулятор дистилляции до воды
Ориентируясь по объему браги и содержанию в ней спирта, сервис рассчитывает предполагаемый выход самогона и объем барды в перегонном кубе, который останется после дистилляции.
Идет подсчет…
Введите слева исходные данные
На выходе должно получиться собранного дистиллята
и барды в кубе
Калькулятор чистого спирта и отбора голов
Рассчитывает количество спирта в дистилляте первой перегонки и определяет объем «голов» в зависимости от указанного процента. Крепость напитка желательно измерять при температуре 20 °C.
Идет подсчет…
Введите слева исходные данные
Оптимальная кислотность сусла
Среда кислотностью 4,0-4,5 рН помогает брожению и препятствует развитию нежелательных бактерий. Коррекцию сусла делают перед внесением дрожжей. Для этого можно использовать лимонную кислоту или сок (5 грамм кислоты эквивалентно соку одного среднего лимона). Для определения начальной кислотности сусла нужен хотя бы самый простой pH-метр.
Идет подсчет…
Введите слева исходные данные
Для разведения понадобится всего кислоты, т.е. на один литр.
Коррекция показаний ареометра в зависимости от температуры
Замерять крепость самогона (дистиллята) нужно строго при температуре 20 °C, иначе ареометр покажет неправильное значение, таков физический принцип его работы. Калькулятор позволяет узнать реальную крепость при другой температуре самогона.
Идет подсчет…
Введите слева исходные данные
Реальная крепость: % (об.)
На данный момент лучшим калькулятором для самогонщиков в виде приложения для операционных систем семейства «Windows» является программа авторства Rudy, которая распространяется бесплатно. Скачать CalcSam v4.3.
Тор
Перейти к площади или объему поверхности.
Факты о Торе
Обратите внимание на эти интересные вещи:
- Это можно сделать, вращая маленький круг
(радиус r ) по линии, составленной из
большего круга (радиус R ). - Не имеет ребер и вершин
- Это , а не многогранник
Тор в небе .
Тор — такое красивое твердое тело,
это было бы весело на пляже!
Площадь
| Площадь поверхности | = (2πR) × (2πr) |
| = 4 × π 2 × R × r |
Пример: r = 3 и R = 7
Площадь поверхности = 4 × π 2 × R × r
= 4 × π 2 × 7 × 3
= 4 × π 2 × 21
= 84 × π 2
≈ 829
Формулу часто записывают так коротко:
Площадь поверхности = 4π 2 Rr
Объем
| Объем | = (2πR) × (πr 2 ) |
| = 2 × π 2 × R × r 2 |
Пример: r = 3 и R = 7
Объем = 2 × π 2 × R × r 2
= 2 × π 2 × 7 × 3 2
= 2 × π 2 × 7 × 9
= 126 π 2
≈ 1244
Формулу часто записывают так коротко:
Объем = 2π 2 Rr 2
Примечание. Формулы площади и объема работают только в том случае, если тор имеет отверстие!
Как цилиндр
Объем : объем такой же, как если бы мы «развернули» тор в цилиндр (длиной 2 π R):
Когда мы его разворачиваем, то, что теряется во внешней части тора, идеально уравновешивается тем, что получается во внутренней части.
Площадь поверхности : то же самое верно для площади поверхности, не включая основание цилиндра.
А знаете ли вы, что Torus был
Латинское слово для подушки ?
(Это не настоящая римская подушка , это просто иллюстрация, которую я сделал)
Расчеты объема и площади не будут работать с этой подушкой, потому что в ней нет отверстия.
Когда у нас более одного тора, они называются тори
Другие изображения Torus
По мере того, как малый радиус ( r ) становится все больше и больше, тор превращается из шины в Пончик:
Формулы и калькулятор для тороидальных индукторов
Тороидальные индукторы часто используются в приложениях для импульсной подачи энергии и регулирования мощности, поскольку магнитные поля в значительной степени ограничены объемом формы.Все формулы на этой странице показаны для тороидального индуктора с воздушным сердечником. Если использовать магнитный сердечник в качестве формы для намотки тороида, индуктивность тороида можно найти, вычислив значение по соответствующей формуле, показанной ниже для индуктора с воздушным сердечником, а затем умножив это значение на относительную проницаемость магнитного сердечника. основной материал.
Тороиды могут быть намотаны круглой формы, как показано на рисунке ниже:
Схема тороидального индуктора круглого сечения
Индуктивность такого тороида можно рассчитать по следующей формуле:
Уравнение для тороидального индуктора круглого сечения
, где N — количество витков, R — средний радиус формы, показанной на рисунке (в см), а a — радиус обмоток формы, как показано на рисунке (в см).
Другая формула индуктивности тороида круглого сечения показана ниже:
Альтернативная формула для тороидального индуктора круглого сечения
, где N — количество витков, D — средний диаметр формы, показанной на рисунке (в дюймах), а d — диаметр витков, как показано на рисунке (в дюймах).
Они также могут иметь прямоугольную форму, как показано на рисунке ниже:
Схема тороидального индуктора квадратного сечения
Индуктивность тороида прямоугольного сечения может быть найдена из следующего уравнения (Terman, Frederick E., Radio Engineers Handbook , McGraw-Hill, New York, 1943, p58.):
Уравнение для тороидального индуктора с квадратным поперечным сечением
, где N — количество витков, h — высота обмотки (в дюймах), d 1 — внутренний диаметр (в дюймах), а d 2 — внешний диаметр (в дюймах).
Вторая формула для тороида прямоугольной формы показана ниже:
Альтернативное уравнение для тороидального индуктора с квадратным поперечным сечением
, где N — количество витков, h — высота обмотки (в см), r 1 — внутренний радиус (в см), а r 2 — это внешний радиус (в см).
Калькуляторы, представленные ниже, могут использоваться для определения правильных параметров тороидальной индуктивности круглого или квадратного сечения. Кредит за исходный код Javascript, используемый в калькуляторе, дан Рэю Аллену, у которого есть несколько подобных полезных калькуляторов на своем веб-сайте Pulsed Power Portal.
Консультации, комментарии и предложения направляйте по адресу [email protected]
Твердые тела — объемы и поверхности
Куб
Объем
V = a 3 (1)
где
V = объем (м 3 , футы 3 ) )
a = сторона (м, футы)
Площадь поверхности
A 0 = 6 a 2 (1b)
где
A 0 = площадь поверхности (м 2 , фут 2 )
Диагональ
d = a 3 1/2 (1c)
где
d = внутренняя диагональ (м, фут)
Диагональ кубической грани
d s = a 2 1/2 (1d)
Кубоид — квадратная призма
90 005
Объем
V = abc (2)
где
V = объем твердого тела (м 3 , футы 3 )
a = длина прямоугольной призмы (м , футы)
b = ширина прямоугольной призмы (м, футы)
c = высота прямоугольной призмы (м, футы)
Диагональ
d = (a 2 + b 2 + c 2 ) 1/2 (2b)
Площадь поверхности
A 0 = 2 (ab + ac + bc) (2c)
где
A 0 = площадь поверхности твердого тела (м 2 , футы 2 )
Параллелепипед 9005 8
Объем
V = A 1 h (3a)
где
A 1 = боковая площадь (м 2 , футы 2 )
Соответствующие Компоненты Sketchup из Engineering ToolBox
- Геометрические фигуры — цилиндры, прямоугольники, конусы, плоскости, сферы, линии, кривые и многое другое..
— бесплатный плагин Engineering ToolBox для использования с потрясающим приложением для рисования / моделирования Sketchup 3D.
Цилиндр
Объем
V = π r 2 h = ( π / 4) d 2 h (4a)
61
61 где d = диаметр цилиндра (м, футы)
r = радиус цилиндра (м, футы)
h = высота цилиндра (м, футы)
Поверхность
A = 2 π rh + 2 π r 2 (4b)
Полый цилиндр
Объем
V = π / 4 ч (D 2 — d 2 ) (5)
Пирамида
Объем
V = 1/3 ч A 1 (6)
где
A 1 90 230 = площадь основания (м 2 , фут 2 )
h = перпендикулярная высота пирамиды (м, фут)
Поверхность
A = ∑ сумма площадей треугольников, образующих стороны + A b (6b)
где
площади поверхности треугольных граней будут иметь разные формулы для оснований разной формы
Frustum of Pyramid
Объем
V = h / 3 (A 1 + A 2 + (A 1 A 2 ) 1/2 ) (7)
Конус
Объем
V = 1/3 π r 2 h (8a)
где
r = радиус основания конуса (м, футы)
h = высота конуса (м, футов)
Поверхность
A = π rl + π r 2 (8b)
где
l = (r 2 + h 2 ) 1/2 = длина стороны конуса (м, футы)
Сторона
м = (h 2 + r 2 ) 1/2 (8c)
A 2 / A 1 = x 2 / h 2 (8d)
Уголок конуса
Объем
V = π / 12 h (D 2 + D d + d 2 ) (9a)
m = (((D — d) / 2) 2 + h 2 ) 1/2 (9c)
Сфера
Объем
V = 4/3 π r 3
= 1/6 π d 3 (10a)
где
r = радиус сферы (м, фут)
Поверхность
A = 4 π r 2
= π d 2 (10b)
c радиус
фут
9 мин. :
Поверхность:
Сферы дробного диаметра — площадь поверхности и объем
Зона сферы
V = π / 6 h (3a 2 + 3b 2 + h) ( 11a)
A m = 2 π rh (11b)
A 0 = π (2 rh + a 2 + b 2 ) (11c)
Сегмент сферы
V = π / 6 ч (3/4 с 2 + h 2 )
= π h 2 (r — h / 3) (12a)
A м = 2 π rh
= π / 4 (s 2 + 4 h 2 ) (12b)
Сектор сферы
V = 2/3 π r 2 h (13a)
A 0 = π / 2 r (4 ч + с) (13b)
Сфера с цилиндрическим растачиванием
V = π / 6 ч 3 (14a)
A 90 229 0 = 4 π ((R + r) 3 (R — r)) 1/2
= 2 π h (R + r) (14b)
h = 2 (R 2 — r 2 ) 1/2 (14c)
Сфера с коническим растачиванием
V = 2/3 π R 2 h (15a)
A 0 = 2 π R (h + (R 2 — h 2 /4) 1/2 ) (15b)
h = 2 (R 2 — r 2 ) 1/2 (15c)
Тор
V = π 2 /4 D d 2 (16a)
A 0 = π 2 D d (16b)
Нарезанный цилиндр
V = π / 4 d 2 h
= π r 2 ((h 1 h 2 ) / 2) (17a)
A m = π dh
= 2 π r ((h 1 902 + h 9022) / 2) (17b)
где
A м = площадь боковых стенок
A 0 = π r (h 1 + h + r + (r 2 + (h 1 — h 2 ) 2 /4) 1/2 ) (17c)
где
A 0 знак равно площадь поверхности
Ungula
V = 2/3 r 2 h (18a)
A m = 2 rh (18b)
29 025 = A м + π / 2 r 2 + π / 2 r (r 2 + h 2 ) 1/2 (18c)
Ствол
V ≈ π / 12 ч (2 D 2 + d 2 ) (19a)
Гравитационный потенциал однородного кругового тора: новый подход | Ежемесячные уведомления Королевского астрономического общества
Аннотация
Получено интегральное выражение для гравитационного потенциала однородного кругового тора, составленного из бесконечно тонких колец.Найдены приближенные выражения для потенциала тора во внешней и внутренней областях. Показано, что во внешней области потенциал тора примерно равен потенциалу бесконечно тонкого кольца той же массы; это справедливо до поверхности тора. В первом приближении показано, что внутренний потенциал тора (внутри тела тора) является квадратичной функцией координат. Предлагается метод сшивания внутреннего и внешнего потенциалов. Этот метод обеспечивает непрерывное приближенное решение для потенциала и его производных, работающих во всем регионе.
1 ВВЕДЕНИЕ
Тороидальные структуры в настоящее время обнаружены в астрофизических объектах разного типа. Примерами таких объектов являются кольцевые галактики, в которых наблюдается кольцо из звезд. Считается, что в некоторых галактиках кольцеобразное распределение звезд происходит из-за столкновений галактик, например, в M31 (Блок и др., 2006) и Arp 147 (Гербер, Лэмб и Балсара, 1992). Анализ данных Sloan Digital Sky Survey (SDSS) (Ибата и др., 2003) указывает на существование звездного кольца в Млечном Пути с масштабами примерно 15–20 кпк, которое, как полагают, возникло в результате захвата карликовой галактики.Затемняющие торы наблюдаются в центральных областях активных ядер галактик (AGN) (Jaffe et al. 2004) и играют важную роль в единой схеме (Antonucci 1993; Urry & Padovani 1995). Кольцеобразные структуры присутствуют и в темной материи. Примером может служить скопление галактик C10024 + 17, где кольцевая структура была обнаружена в распределении темной материи с использованием методов гравитационного линзирования (Jee et al. 2007). В Млечном Пути кривые вращения вместе с данными EGRET можно объяснить существованием двух колец темной материи, расположенных на расстояниях примерно 4 и 14 кпк от Центра Галактики (de Boer et al.2005). Такие тороидальные структуры могут обладать значительной массой и, таким образом, гравитационно влиять на движение материи.
Б. Риман посвятил одну из своих последних работ гравитационному потенциалу однородного тора (Риман, 1948). Однако эта работа осталась незавершенной. Более века гравитационному потенциалу тора не уделялось внимания. 1 Кондратьев (2003) впервые вернулся к этой проблеме. В этой работе было получено точное выражение для потенциала однородного тора на оси симметрии.В работе Кондратьева (2007) было найдено интегральное выражение для потенциала однородного тора с использованием диска в качестве первичного гравитирующего элемента. Сложение таких дисков в стопку приведет к образованию тора с потенциалом, равным сумме потенциалов составляющих дисков. Однако очевидно, что любые интегральные выражения проблематичны для использования как в аналитических исследованиях, так и при численном интегрировании уравнений движения, а также при решении задач гравитационного линзирования. Кондратьев и др. (2009) и Кондратьев и Трубицина (2010) получили разложение потенциала тора по рядам Лапласа, но показали, однако, что такое разложение невозможно внутри некоторых сферических оболочек.
В этой статье мы предлагаем новый подход к исследованию гравитационного потенциала тора. Особое внимание было уделено поиску приближенных выражений для потенциала, которые упростили бы исследование астрофизических объектов с гравитирующими торами в качестве структурных элементов. В отличие от Кондратьева (2007), мы использовали бесконечно тонкое кольцо в качестве компонента тора. Такое кольцо на самом деле является реализацией тора, малый радиус которого стремится к нулю, а большой равен радиусу кольца.Используя такой подход, мы получили интегральное выражение для потенциала однородного кругового тора (раздел 2) и приближенные выражения для потенциала во внешней (раздел 3) и внутренней (раздел 4) областях. В разделе 5 предлагается метод определения торического потенциала для всей области.
2 ГРАВИТАЦИОННЫЙ ПОТЕНЦИАЛ ОДНОРОДНОГО ТОРА
Составьте тор с массой M , внешним (большим) радиусом R и малым радиусом R 0 из набора бесконечно тонких колец, далее составляющих колец (см.рис.1), причем их плоскости параллельны плоскости симметрии тора. Выберите центральное кольцо с массой M c и радиусом R из набора колец, составляющих тор. Потенциал, создаваемый этим кольцом в произвольной точке P ( x , z ), имеет вид 1, где безразмерный потенциал бесконечно тонкого кольца равен 2, где — полный эллиптический интеграл первого рода и его параметр равно 3 Потенциал в точке P ( x , z ), создаваемой произвольным кольцом с радиусом R ′ и массой M r , расположенным в торе на высоте z ′ ( Инжир.1) имеет вид 4, где выражение для φ r получается подстановкой в (2) вида и . Обозначим координату кольца 2 , отсчитываемую от центра поперечного сечения тора (рис.1) как x ′ = R ′ — R , и, следовательно, его радиус равен R ′ = R + x ′. Удобно ввести безразмерные координаты η ′ = x ′ / R , ζ ′ = z ′ / R и ρ = x / R , ζ = z / R . что приведет к выражению для безразмерного потенциала формы 5, где 6 Из условия однородности тора отношения массы к радиусу для центрального и произвольного кольца компонентов одинаковы и, таким образом, M c = M r / (1 + η ′).Выражение для потенциала составляющего кольца тогда 7, где φ r определяется выражениями (5) и (6). Благодаря аддитивности потенциал тора можно представить в виде интеграла по потенциалам компонентных колец. Для этого заменим дискретную массу кольца M c в (7) на дифференциал d M , который для однородного тора равен d M = [ M / (π r 2 0 )] dη ′ dζ ′, где M — полная масса тора, равная сумме масс составляющих колец, а r 0 = R 0 / R — безразмерный малый радиус тора (геометрический параметр).Тогда потенциал однородного кругового тора принимает вид 8 Это интегральное выражение для потенциала тора справедливо как для внутренней, так и для внешней точек. Справедливость выражения (8) подтверждается расчетом потенциала прямым интегрированием по объему тора. В дальнейшем, анализируя приближенные выражения, мы будем использовать термин «точные» для значений потенциала, полученных из интегральной формулы (8). На рис. 2 представлены зависимости потенциала тора от радиальной координаты; они были получены численно по формуле (8) для торов с разными значениями геометрического параметра r 0 .Видно, что потенциальные кривые для всех значений r 0 вписаны в потенциальную кривую бесконечно тонкого кольца той же массы и радиуса, расположенного в плоскости симметрии тора. Потенциальная кривая справа от поверхности тора (ρ> 1 + r 0 ) практически совпадает с потенциальной кривой кольца, а слева (ρ r 0 ) проходит ниже и отличается на величину, зависящую от r 0 (см. раздел 3).На рис. 3 представлены зависимости потенциала тора от радиальной координаты; они были рассчитаны по выражению (8) для различных значений ζ.
Рисунок 1
Вверху: 3D-схема конфигурации тора; внизу: схематический разрез тора в виде набора бесконечно тонких колец.
Рисунок 1
Вверху: 3D-схема конфигурации тора; внизу: схематический разрез тора в виде набора бесконечно тонких колец.
Рисунок 2
Зависимость потенциала от радиальной координаты для ζ = 0, для торов с различными значениями геометрического параметра: (1) r 0 = 0.05, (2) r 0 = 0,1, (3) r 0 = 0,2, (4) r 0 = 0,3, (5) r 0 = 0,4. Потенциал бесконечно тонкого кольца (1) с массой M , равной массе тора, показан штриховой линией. На этом графике и на всех последующих рисунках M = 1, R = 1, G = 1.
Рисунок 2
Зависимость потенциала от радиальной координаты при ζ = 0 для торов с различными Значения геометрического параметра: (1) r 0 = 0.05, (2) r 0 = 0,1, (3) r 0 = 0,2, (4) r 0 = 0,3, (5) r 0 = 0,4. Потенциал бесконечно тонкого кольца (1) с массой M , равной массе тора, показан штриховой линией. На этом графике и на всех последующих рисунках M = 1, R = 1, G = 1.
Рисунок 3
Потенциал тора при r 0 = 0.3 как функция радиальной координаты для различных значений ζ = 0, 0,1, 0,2, 0,3, 0,4.
Рисунок 3
Потенциал тора с r 0 = 0,3 как функция радиальной координаты для различных значений ζ = 0, 0,1, 0,2, 0,3, 0,4.
Отметим, что в отличие от работы Кондратьева (2007, с. 196, выражение 7.26), где потенциал тора выражается только через однократное интегрирование эллиптических интегралов всех трех видов, потенциал тора (8) в нашем работа выражается двойным интегрированием эллиптического интеграла первого рода.Однако дальнейший анализ этого выражения для потенциала тора (8) позволяет получить приближения, которые являются физически понятными и позволяют решать практические астрофизические задачи, требующие многократных вычислений гравитационного потенциала тора.
Для дальнейшего анализа потенциала тора мы определяем внутреннюю область как объем, ограниченный поверхностью тора (внутри тела тора), а внешнюю область как область вне этой поверхности.
3 ТОРУСНЫЙ ПОТЕНЦИАЛ ВО ВНЕШНЕМ РЕГИОНЕ
Из рис.2 видно, что внешний потенциал тора может быть приближенно представлен потенциалом бесконечно тонкого кольца той же массы до поверхности тора. При ρ → 0 значения потенциала тора и потенциала бесконечно тонкого кольца различаются на величину, зависящую от геометрического параметра r 0 , что особенно заметно для толстого тора ( r 0 > 0,5). Мы находим связь между внешним потенциалом тора и потенциалом кольца той же массы, т.е.е. получить приближенное выражение для потенциала тора во внешней области, где выполняется условие (ρ — 1) 2 + ζ 2 ≥ r 2 0 . Внутри этой области подынтегральное выражение φ r (ρ, ζ; η ′, ζ ′) в (8) не имеет особенностей для всех η ′, ζ ′; поэтому его можно разложить в ряд Маклорена по степеням η ′, ζ ′ в окрестности точки η ′ = ζ ′ = 0. Поскольку интегралы в симметричных пределах от членов ряда, которые содержат кросс-производные и производные нечетных порядки равны нулю, в разложении остаются только слагаемые с четными порядками.При ограничении квадратичных членов ряда потенциал кольца компонентов равен 9 Подставив (9) в (8), мы получим после интегрирования 10 В конечном итоге приближенное выражение для потенциала тора во внешней области (ρ — 1 ) 2 + ζ 2 ≥ r 2 0 имеет вид 11 где — безразмерный потенциал центрального кольца (2), а 12 — полный эллиптический интеграл второго рода. Мы можем удобно перейти к новой переменной η = ρ− 1, которая позволяет представить выражение (12) как 13, где выражение (11) для торического потенциала (далее мы будем называть его S-приближением) с (12) или (13) с учетом (13) достаточно точно представляет потенциал тора во внешней области η 2 + ζ 2 ≥ r 2 0 (рис.2). Поскольку ∣ S ∣≤ 1, второй множитель в (11) является медленно меняющейся функцией ρ и ζ. Упростим выражение (11), заменив второй множитель его асимптотическими приближениями. В первом случае ρ → 0 соответствует η → −1, параметру m → 0 и E ( m ) / K ( м ) → 1, следовательно, S → (ζ 2 — 1) / (ζ 2 + 1). Выражение для потенциала тора в этом случае равно 14 Поскольку безразмерный потенциал кольца (2) на оси симметрии равен, для тора получаем 15 и для ζ = 016 Второе слагаемое ( GM / R × r 2 0 /8) в (16) описывает смещение потенциала тора на оси симметрии по сравнению с потенциалом бесконечно тонкого кольца (рис.2). Во втором случае при больших η параметр m → 0 и S → 1 в (11), поэтому 17 т.е. потенциал тора равен потенциалу бесконечно тонкого кольца с той же массой M и радиус R в данном случае. Из рис. 4 видно, что S-приближение для внешнего потенциала тора применимо до поверхности тора (верхние кривые). Действительно, в области ρ≤ 1 — r 0 разница между потенциалом, полученным из интегрального выражения (8), и его значением, взятым из S-приближения, достигает максимума вблизи поверхности тора и не превышает 0 .2 процента для r 0 = 0,5. Разница остается небольшой даже для толстого тора: она не превышает 1,5% для r 0 = 0,9. При ζ = r 0 все точки внешние и кривые для точного потенциала и S-приближения практически совпадают (отклонение менее 0,1%).
Рисунок 4
Зависимость потенциала тора при r 0 = 0,5 от ρ для ζ = 0 (верхние кривые) и ζ = 0.5 (нижние кривые). Сплошными линиями показан потенциал, рассчитанный по точной формуле (8). S-приближение (11) потенциала показано пунктирными линиями, а пунктирные линии представляют предельные случаи S-приближения: потенциальная кривая для бесконечно тонкого кольца (17) находится справа от поперечного сечения тора а кривая, представляющая «сдвинутый» потенциал бесконечно тонкого кольца (14), находится слева. Границы поперечного сечения тора — пунктирные вертикальные линии.
Рисунок 4
Зависимость потенциала тора от r 0 = 0.5 по ρ при ζ = 0 (верхние кривые) и ζ = 0,5 (нижние кривые). Сплошными линиями показан потенциал, рассчитанный по точной формуле (8). S-приближение (11) потенциала показано пунктирными линиями, а пунктирные линии представляют предельные случаи S-приближения: потенциальная кривая для бесконечно тонкого кольца (17) находится справа от поперечного сечения тора а кривая, представляющая «сдвинутый» потенциал бесконечно тонкого кольца (14), находится слева. Границы поперечного сечения тора — пунктирные вертикальные линии.
Отметим, что асимптотика S-приближения для внешнего потенциала (15) и (17) также достаточно хорошо описывает потенциал тора (пунктирная линия на рис. 4). Таким образом, при | ζ | < r 0 , приближение (15) может быть использовано для оценки потенциала внутри области, ограниченной цилиндром радиусом ρ− r 0 , а приближение (17) применимо вне области, ограниченной цилиндром. цилиндром радиусом ρ + r 0 . При | ζ | 1, выражение (15) стремится к (17), а выражение для потенциала бесконечно тонкого кольца (2) можно использовать во всей внешней области для приближенной оценки потенциала тора.
Следовательно, внешний потенциал тора может быть с хорошей точностью представлен потенциалом бесконечно тонкого кольца той же массы. Зависимость геометрического параметра r 0 проявляется только в отверстии тора; он учитывается в «смещенном» потенциале бесконечно тонкого кольца . Эти приближения справедливы до поверхности тора. 3
4 ТОРУСНЫЙ ПОТЕНЦИАЛ ВО ВНУТРЕННЕМ РЕГИОНЕ
Рисунок 5
Схема поперечного сечения тора.
Рисунок 5
Схема поперечного сечения тора.
Ограничимся случаем тонкого тора ( r 0 ≪ 1). Тогда ( r — r ′) 2 ≪ 4 (1 + η) (1 + η ′) и (1 + η) (1 + η ′) ≈ 1, а первый множитель в (21) можно записать во втором порядке как 22 После разложения квадратного корня в (22) по степеням η и η ′ получим 23. Аналогичным образом второй множитель (в квадратных скобках) в выражении (21) может быть записан , в члены, квадратичные по координатам, as 24 Таким образом, мы получаем следующее выражение для потенциала кольца компонентов: 25 С учетом внутреннего потенциала тора перепишем выражение (8) в полярных координатах (рис.5): 26, где координаты кольца компонентов равны η ′ = r ′ cos θ ′, ζ ′ = r ′ sin θ ′, а координаты точки P равны η = r cos θ. , ζ = r sin θ. Подставим (23) и (24) в (25) и после умножения ограничимся членами, квадратичными по η, ζ и η ′, ζ ′. Тогда после интегрирования (26) получим приближенное выражение для внутреннего потенциала тора: 27 где Первое слагаемое в (27) — значение потенциала тора в центре поперечного сечения тора: c = φ тор (0, 0; r 0 ).Для дальнейшего анализа внутреннего потенциала удобно перейти в систему координат, нормированную на геометрический параметр тора r 0 . Тогда коэффициенты ряда преобразуются к виду. Выражение для потенциала тора (27) можно записать как 28
Из (28) следует, что максимальное значение потенциала достигается в точке η max = — ( a 1 r 0 ) / (2 a 2 ), ζ = 0, а эквипотенциальные линии представляют собой эллипсы, центры которых смещены на величину η max относительно центра поперечного сечения тора, а отношение полуосей эллипсов равно .Отметим, что положение максимума потенциала η = η max , ζ = 0 соответствует точке невесомости, где равнодействующая всех сил, действующих на частицу внутри тора, равна нулю. В таком приближении компоненты силы внутри тора линейно зависят от координат. На рис. 6 представлены кривые внутреннего потенциала в системе координат, нормированные на r 0 для трех значений r 0 .
Рисунок 6
Зависимость внутреннего потенциала от нормированной координаты η / r 0 при ζ = 0 для различных значений геометрического параметра: r 0 = 0.1, 0,2, 0,5. Сплошные кривые — зависимости потенциала от расстояния до центра поперечного сечения тора, рассчитанные по точной формуле (8). Пунктирными линиями показаны потенциальные кривые, полученные с приближенным выражением для внутреннего потенциала тора (28).
Рисунок 6
Зависимость внутреннего потенциала от нормированной координаты η / r 0 при ζ = 0 для различных значений геометрического параметра: r 0 = 0.1, 0,2, 0,5. Сплошные кривые — зависимости потенциала от расстояния до центра поперечного сечения тора, рассчитанные по точной формуле (8). Пунктирными линиями показаны потенциальные кривые, полученные с приближенным выражением для внутреннего потенциала тора (28).
Хотя мы ограничились случаем тонкого тора, кривые потенциала, взятые из выражения (28), согласуются с кривыми для точного потенциала (8) до r 0 = 0.5, где отклонение максимально вблизи поверхности тора и составляет порядка 2% (рис. 6). Значение потенциала в центре поперечного сечения тора [константа c = φ torus (0, 0; r 0 ) в (27)] также совпадает с его точным значением.
Представляет интерес исследование решений, полученных для предельных случаев. Действительно, корпус r 0 = R 0 / R → 0 соответствует двум ограничивающим проходам, бесконечно тонкому кольцу (когда R закреплен, а R 0 → 0 ) и к цилиндру (когда R 0 зафиксировано и ).Остановимся на предельном переходе к потенциалу цилиндра. При R 0 → 0 коэффициенты c → 1-2 ln k , a 1 → 0, а коэффициенты a 2 , b 2 → — 1; выражение (28) в этом случае принимает следующий вид: 29 где r 2 = η 2 + ζ 2 . Известно, что внутренний потенциал кругового цилиндра длиной 2 H , намного превышающий радиус R 0 его поперечного сечения (Кондратьев 2007), имеет вид 30 После формальной замены 2 H = 2π R в (30) (длина цилиндра равна длине центрального кольца), получаем выражение 31 Выражение (31) совпадает с (29) за исключением константы. 4 Квадратичная зависимость внутреннего потенциала тонкого тора от r может быть также получена в случае, когда малый радиус R 0 → 0. Внешний потенциал тора был показан в разделе 3. быть примерно равным потенциалу бесконечно тонкого кольца той же массы и радиуса. В этом случае, чем меньше геометрический параметр тора r 0 , тем точнее будет это приближение. Следовательно, при η 2 + ζ 2 ≥ r 0 → 0 внешний потенциал тора стремится к потенциалу бесконечно тонкого кольца.В этом случае η, ζ → 0 и, следовательно, эллиптический интеграл в выражении для бесконечно тонкого кольца (2) может быть разложен в окрестности м → 1. Если мы ограничимся первым членом разложения, мы получаем приближенное выражение для потенциала центрального бесконечно тонкого кольца 32, которое остается справедливым и для внешнего потенциала тонкого тора. Следует отметить отсутствие зависимости от r 0 , поскольку в таком приближении все тонкие торы с одинаковыми массами и большими радиусами являются экгравитирующими по внешнему потенциалу.Тогда производные внешнего потенциала тонкого тора по η, ζ равны и на поверхности тора принимают следующий вид (η 2 + ζ 2 = r 2 0 ): линейная зависимость силы от координат η, ζ, удовлетворяющая таким граничным условиям. Таким образом, внутренний потенциал тонкого тора можно представить в виде 33, где c ( r 0 ) — постоянная интегрирования. Приравнивая (32) к (33) на поверхности тора, получаем выражение для константы c ( r 0 ) = −2ln ( r 0 /8) + 1, которое совпадает с выражением (27), полученное выше при r 0 ≪ 1.
5 ШИТЬЕ ВНУТРЕННЕГО И НАРУЖНОГО ПОТЕНЦИАЛОВ НА ПОВЕРХНОСТИ ТОРУСА
В предыдущих разделах мы получили приближенные выражения для потенциала тора во внешнем (η 2 + ζ 2 ≥ r 2 0 ) и внутреннем (η 2 + ζ 2 ≤ r 2 0 ) регионов. Также было показано, что внутренний потенциал тора может быть представлен рядом по степеням η / r 0 и ζ / r 0 , а также постоянными, линейными и квадратичными членами ряда определены аналитически.Чтобы найти большее количество членов ряда, достаточное для достаточно точного представления внутреннего потенциала, и получить непрерывное приближенное решение для потенциала и его производных во всей области, которое будет удовлетворять граничным условиям на поверхности, мы будем действовать следующим образом: способ. Представим внутренний потенциал тора в виде степенного ряда 5 : 36, где c ( r 0 ), a i ( r 0 ), b j ( r 0 ), t ij ( r 0 ) — неизвестные коэффициенты.Заметим, что ряд (36) содержит только члены с четными степенями ζ, поскольку потенциал тора симметричен по ζ. Предположим, что у нас есть аналитическое выражение для потенциала тора Ψ (η, ζ; r 0 ) на его поверхности (η 2 + ζ 2 = r 2 0 ). Также запишем внутренний потенциал тора (36) на его поверхности (η = r 0 cos θ и ζ = r 0 sin θ) как 37 Из условий равенства внутреннего и внешнего потенциала и его производных в координатах на поверхности тора для нескольких углов θ k , получаем систему из 3 линейных уравнений k для определения коэффициентов c , a i , b j , t ij : 38 Таким образом, если бы у нас было аналитическое решение для внешнего потенциала тора, мы могли бы получить точное выражение для внутреннего потенциала в виде бесконечного ряда по степеням cos θ k , sin θ k , используя граничные условия и решая систему уравнений (38).Поскольку аналитического выражения для внешнего потенциала нет, можно использовать приведенное выше приближенное выражение (11) для потенциала тора во внешней области (S-приближение) и ввести обозначения, где φ в , φ из — решения для внутреннего (37) и внешнего (11) потенциалов на границе тора соответственно. Неизвестные коэффициенты ряда затем могут быть определены из условия минимального значения функционала: 39 Функционал (39) минимизирован методом наименьших квадратов, а коэффициенты ряда (37) определены с точностью до четвертой степени. .Коэффициенты ряда представлены в Приложении A (Таблица A1). На рис.7 для всей области представлена зависимость потенциала от радиальной координаты из точного выражения (8), а также ее приближенное решение, полученное сшивкой S-приближения (11) и внутреннего потенциала (37 ). Хотя приближенные решения были получены в предположении, что тор тонкий, r 0 ≪ 1, мы видим, что точное (8) и приближенное решения согласованы даже для тора с r 0 = 0.5. На рис. 8 показаны эквипотенциальные кривые на плоскости поперечного сечения тора, где также видно хорошее согласие для всех значений ρ, ζ.
Таблица A1
Коэффициенты степенного ряда для внутреннего потенциала тора для различных значений r 0 , полученных методом сшивания.
| Коэфф. | Геометрический параметр r 0 | |||||||||
| 0,1 | 0.2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | ||
| а 1 | −0,33798 | −0,53651 | −0,68154 | 942 | −0,87439 | −0,93587 | −0,97906 | −1,00628 | −1,01928 | |
| a 2 | −0,98002 | −0.93543 | −0,87773 | −0,81171 | −0,74107 | −0,66865 | −0,59677 | −0,52739 | −0,46224 | |
| b 2 | 3 42 | 2 | 3 42 9004 9001 9004 9004 9004 9001 1.01970 | -1,02892 | -1,03759 | -1,04495 | -1,05030 | -1,05299 | -1,05237 | |
| a 3 | 0.02392 | 0,04364 | 0,05781 | 0,06608 | 0,06853 | 0,06550 | 0,05753 | 0,04525 | 0,02938 | |
| t 12 | 0,02550 | 0,02550 9004 | 0,19323 | 0,23295 | 0,27238 | 0,30991 | ||||
| а 4 | -0.00182 | −0,00785 | −0,01610 | −0,02576 | −0,03580 | −0,04535 | −0,05371 | −0,06036 | −0,06495 | |
b | 0,00308 | 0,00570 | 0,00922 | 0,01362 | 0,01880 | 0,02453 | 0,03045 | | |||
| t 22 | -0.00122 | −0,00812 | −0,01948 | −0,03681 | −0,06076 | −0,09157 | −0,12900 | −0,17213 | −0,21931 | |
| Coeff. | Геометрический параметр r 0 | ||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |||
| a 1 | -0.33798 | −0,53651 | −0,68154 | −0,79129 | −0,87439 | −0,93587 | −0,97906 | −1,00628 | −1,01928 | ||
а | 0,93543 | −0,87773 | −0,81171 | −0,74107 | −0,66865 | −0,59677 | −0,52739 | −0,46224 | | |||
| b 2 | −1.00411 | -1,01086 | -1,01970 | -1,02892 | -1,03759 | -1,04495 | -1,05030 | -1,05299 | -1,05237 | ||
| а | 0,05781 | 0,06608 | 0,06853 | 0,06550 | 0,05753 | 0,04525 | 0,02938 | ||||
| т 12 | 0.02550 | 0,05329 | 0,08404 | 0,11791 | 0,15454 | 0,19323 | 0,23295 | 0,27238 | 0,30991 | ||
| a 4 | -0,001802 -0,004 9002 | −0,03580 | −0,04535 | −0,05371 | −0,06036 | −0,06495 | |||||
| b 4 | 0.00061 | 0,00131 | 0,00308 | 0,00570 | 0,00922 | 0,01362 | 0,01880 | 0,02453 | 0,03045 | ||
| т 22 | -0,00122 | -0,0042 | -0,00122 | -0,004 900 0,03681 | −0,06076 | −0,09157 | −0,12900 | −0,17213 | −0,21931 | ||
Таблица A1
Коэффициенты степенного ряда для внутреннего потенциала тора для различных значений r 0 , полученные методом шитья.
| Коэфф. | Геометрический параметр r 0 | ||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |||
| a 1 | −0,33798 | −0,53651 | −0,68154 | −0,79129 | −0,87439 | −0,93587 | −0.97906 | -1,00628 | -1,01928 | ||
| а 2 | -0,98002 | -0,93543 | -0,87773 | -0,81171 | -0,74107 43 | -0,642 | -0,74107 43 | -0,642 0,52739 | -0,46224 | ||
| b 2 | -1,00411 | -1,01086 | -1,01970 | -1,02892 | -1,03759 | -1.04495 | −1.05030 | −1.05299 | −1.05237 | ||
| а 3 | 0,02392 | 0,04364 | 0,05781 | 0,06608 | 0,06853 | 0,06550 0,06608 | 0,06853 | 0,06550 | |||
| т 12 | 0,02550 | 0,05329 | 0,08404 | 0,11791 | 0,15454 | 0.19323 | 0,23295 | 0,27238 | 0,30991 | ||
| a 4 | −0,00182 | −0,00785 | −0,01610 | −0,02576 | −0,042 −35042 | −0,06036 | −0,06495 | ||||
| b 4 | 0,00061 | 0,00131 | 0,00308 | 0,00570 | 0.00922 | 0,01362 | 0,01880 | 0,02453 | 0,03045 | ||
| т 22 | −0,00122 | −0,00812 | −0,01948 | −0,03681 76| −0,09 | −0,03681 76 | −0,09 | 0,12900 −0,17213 | −0,21931 | | ||
| Коэфф. | Геометрический параметр r 0 | |||||||||
| 0.1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | ||
| a 1 | −0,33798 | −0,53651 | −0,68154 900 | −0,79129 | −0,87439 | −0,93587 | −0,97906 | −1,00628 | −1,01928 | |
| a 2 | −0.98002 | −0,93543 | −0,87773 | −0,81171 | −0,74107 | −0,66865 | −0,59677 | −0,52739 | −0,46224 | |
| b −0,46224 | b 304 900 1,01086 | -1,01970 | -1,02892 | -1,03759 | -1,04495 | -1,05030 | -1,05299 | -1,05237 | a 3 | 0.02392 | 0,04364 | 0,05781 | 0,06608 | 0,06853 | 0,06550 | 0,05753 | 0,04525 | 0,02938 | t 12 | 0,02550 | 0,02550 9004 | 0,19323 | 0,23295 | 0,27238 | 0,30991 | а 4 | -0.00182 | −0,00785 | −0,01610 | −0,02576 | −0,03580 | −0,04535 | −0,05371 | −0,06036 | −0,06495 | b | 0,00308 | 0,00570 | 0,00922 | 0,01362 | 0,01880 | 0,02453 | 0,03045 | t 22 | -0.00122 | −0,00812 | −0,01948 | −0,03681 | −0,06076 | −0,09157 | −0,12900 | −0,17213 | −0,21931 | |
Рисунок 7
Зависимость потенциала тора от ρ для r 0 = 0,5 (ζ = 0) во всей области: потенциальная кривая, рассчитанная по точному выражению (8), показана сплошной линией, а пунктирная линия показывает результат сшивания S-приближения во внешней области (11) и внутреннего потенциала, представленного степенным рядом (37) с коэффициентами, найденными из условия сшивания (39).
Рисунок 7
Зависимость потенциала тора от ρ для r 0 = 0,5 (ζ = 0) во всей области: потенциальная кривая, рассчитанная по точному выражению (8), показана сплошной линией, в то время как пунктирная линия демонстрирует результат сшивания S-приближения во внешней области (11) и внутреннего потенциала, представленного степенным рядом (37) с коэффициентами, найденными из условия сшивания (39).
Рисунок 8
Эквипотенциальные кривые для тора с r 0 = 0.5. Сплошные линии — линии, рассчитанные по точному выражению для потенциала; пунктирными линиями обозначены приблизительные формулы для внешнего и внутреннего потенциалов (см. подпись к рис. 7). Поперечное сечение тела тора обозначено серым кружком.
Рисунок 8
Эквипотенциальные кривые для тора с r 0 = 0,5. Сплошные линии — это линии, рассчитанные по точному выражению для потенциала; пунктирными линиями обозначены приближенные формулы для внешнего и внутреннего потенциалов (см. рис.7 подпись). Поперечное сечение тела тора обозначено серым кружком.
6 ВЫВОДЫ
В данной работе подробно исследуется гравитационный потенциал однородного кругового тора. Интегральное выражение для потенциала, справедливое для произвольной точки, получается составлением тора из бесконечно тонких колец. Такой подход позволил найти приближенное выражение для внешнего потенциала тора (S-приближение), имеющее достаточно простой вид.Показано, что внешний потенциал тора может быть с хорошей точностью представлен потенциалом бесконечно тонкого кольца той же массы. Зависимость геометрического параметра r 0 проявляется только в отверстии тора; он учитывается в «сдвинутом» потенциале бесконечно тонкого кольца. Эти приближения справедливы до поверхности тора.
Для внутреннего потенциала найдено приближенное выражение в виде степенного ряда с точностью до членов второго порядка, где коэффициенты зависят только от геометрического параметра r 0 .Получены выражения для потенциала в центре поперечного сечения тора и для координат максимума потенциала, рассмотрен предельный переход к потенциалу цилиндра. Показано, что внутренний потенциал тора можно представить как сумму потенциала цилиндра и члена, составляющего геометрическую кривизну поверхности тора. Предлагается метод определения потенциала тора по всей области, который подразумевает «сшивание» на поверхности внешнего потенциала (S-приближение) и внутреннего потенциала, представленного степенным рядом.Этот метод обеспечил непрерывное приближенное решение для потенциала и его производных, работающее во всем регионе.
Конечно, распределение вещества внутри тора в реальных астрофизических объектах неоднородно, и поперечное сечение тора может отличаться от круглого. Поэтому представляет дальнейший интерес учет неоднородности распределения материи внутри тора, отличия поперечного сечения тора от круглой формы и т. Д.
Эта работа была частично поддержана Национальной программой «CosmoMicroPhysics».
Благодарим профессора В. Конторовичу за полезные предложения и доктору В.С. Цветковой за критическое прочтение оригинальной версии статьи.
ССЫЛКИ
et al. ,
2006
,
Nat
,
443
,
832
et al. ,
2004
,
Nat
,
429
,
47
et al. ,
2007
,
ApJ
,
661
,
728
,
2003
,
Теория потенциала и цифры равновесия
.
Регулярный и хаотический динамический пресс
, Москва-Ижевск
,
2007
,
Теория потенциала. Новые методы и проблемы с решениями
.
Мир
, Москва,
512
с
,
2010
,
Тех. Phys.
,
55
,
22
,
2009
,
Тех. Phys.
,
54
,
176
,
1948
, дюйм
, изд.,
Сборник статей
.
ОГИЗ
, Москва
,
1950
,
Статическое и динамическое электричество
.
McGraw-Hill
, New York
Приложение
ПРИЛОЖЕНИЕ А: КОЭФФИЦИЕНТЫ МОЩНОСТИ ДЛЯ ВНУТРЕННЕГО ПОТЕНЦИАЛА ТОРУСА
В таблице A1 представлены коэффициенты степенного ряда (до четвертой степени) для внутреннего потенциала тора, вычисленные из условия сшивания для тора с различными значениями геометрического параметра r 0 .Аналитическое выражение (28) использовалось для определения нулевого коэффициента c ряда. На рисунке A1 линейные ( a 1 ) и квадратичные ( a 2 , b 2 ) коэффициенты степенного ряда как функции от r 0 , полученные аналитически из ( 27) показаны сплошными линиями; точки — правильные значения этих коэффициентов, полученные из условий шитья (см. Таблицу A1). Видно, что значения аналитических коэффициентов совпадают до r 0 = 0.5 со значениями, полученными независимо с помощью метода шитья из (39).
Рисунок A1
Зависимость первых коэффициентов степенного ряда от r 0 для внутреннего потенциала, полученного методом сшивания.
Рисунок A1
Зависимость первых коэффициентов степенного ряда от r 0 для внутреннего потенциала, полученного методом сшивания.
© 2010 Авторы.Составление журнала © 2010 РАН
Физика 6730 Лабораторное упражнение: интеграция методом Монте-Карло
Основы
Физика 6730 Лабораторное упражнение: интеграция методом Монте-Карло
Основы
Задача, которую мы изучаем, — вычислить объем усеченного бублика.
(тор). Тор описывается двумя радиусами: меньшим, r
и более крупный, R . Начнем с рисования круга радиуса
R в плоскости x-y с центром в начале координат. Делаем этот круг
быть центром цилиндра, который был согнут, чтобы соединиться с самим собой.Цилиндр имеет круглое сечение радиусом r . В
алгебраическими терминами, тор — это множество x, y и z, удовлетворяющих
z 2 + (rho - R) 2 2 rho = sqrt (x 2 + y 2 )
Усеченный бублик проиллюстрирован в числовом формате.
Рецепты на C онлайн, любезно предоставлены издательством Cambridge University Press.
Упражнение 1. Объем усеченного бублика 2D пример
Если нам нужны только координаты объема и центра масс в x и
y, мы можем рассматривать задачу интегрирования как двумерную
интеграл по x и y с подынтегральным выражением, равным длине по z в точке a
учитывая x и y. torus0.c выполняет двумерный интеграл.
Изучите код и ответьте на эти вопросы:
- С точки зрения алгебраической записи в числовых рецептах, что такое
значение подынтегрального выражения объема в точках x, y? - Что измеряет «процент попаданий»?
Запустите код для 10 000 испытаний, чтобы оценить объем и
см. координаты. Затем запустите его для 1000000 испытаний. Сколько стоит
ошибка уменьшилась? Уменьшается ли ошибка пропорционально 1 / sqrt (N)?
Упражнение 2.
Код torus1 выполняет те же вычисления, но образцы в трех
размеры вместо этого с постоянным подынтегральным выражением. Запустите этот код с помощью
10 000 и 1 000 000 испытаний и сравните результаты с результатами
Упражнение 1. Уменьшается ли ошибка пропорционально 1 / sqrt (N)?
Что точнее? Объясните, почему с точки зрения «посещаемости»?
Упражнение 3.
В коде torus2 мы вводим переменную массу, зависящую от z
плотность rho = exp (5 * z) как в числовых рецептах.Есть два
способы справиться с этим: (1) наивный способ, как в torus2 , выборка
равномерно по x, y и z и суммируя плотность и (2) с
выборка важности, как в torus3 . Для этого мы меняем
переменные интегрирования к x, y, s, где
s = ехр (5 * z) / 5 дс = ехр (5z) * дз z = журнал (5 с) / 5
Обратите внимание, что исходное подынтегральное выражение содержит exp (5z) * dz , но
новая интегральная функция содержит всего дс с экспоненциальным множителем
устранено.Таким образом, равномерная выборка по x, y и s может быть более эффективной.
Это называется выборкой по важности.
Попробуйте оба метода и обсудите, что вы найдете.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно.Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.
Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie. - Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом.Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере. - Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.
Вы должны отключить приложение при входе в систему или проконсультироваться с вашим системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Supershapes
Самый быстрый способ войти в это приложение — несколько раз нажать кнопку Randomize (изображение 2 кубиков), расположенную в верхнем левом углу панели Shape Parameters , чтобы сгенерировать несколько случайных фигур.Поскольку не все уравнения формы являются стабильными для всех значений во всем диапазоне их параметров, я проделал небольшую работу, чтобы ограничить рандомизацию разумно допустимыми значениями для каждого типа формы.
Затем вы можете использовать меню вверху, чтобы изменить режим Shape Type и Surface Color , или вы можете использовать сочетания клавиш, указанные в меню, если у вас подключена клавиатура.
Вы можете настроить любой из смежных ползунков для взаимодействия с фигурой в реальном времени.Ползунки параметра формы специфичны для каждого типа формы, тогда как параметры оболочки являются общими для всех и позволяют растягивать и смещать сгенерированную поверхность в формы, подобные оболочке. Регенерация формы должна быть достаточно быстрой на большинстве современных компьютеров и планшетов, но вы можете отключить обновление в реальном времени, если вам нужно, используя меню Slider settings . Кроме того, не все ползунки активны для всех уравнений формы, но вы сможете легко увидеть, когда они включены / отключены.
Фон
Это в основном версия HTML5 одного из моих Java-апплетов. Он вырос из некоторых экспериментов, которые я проводил с использованием сферических гармоник как способа моделирования рассеянного освещения в реальном времени при моделировании затенения. Поскольку я склонен по-настоящему разбираться в вещах только тогда, когда вижу их, недавно я сделал быстрый просмотрщик в Processing, чтобы убедиться, что все расчеты выполняются правильно.
Некоторые визуализации и формы начали выглядеть достаточно интересно, поэтому я немного их отполировал, а затем сделал эту версию WebGL.В конце концов, я включил генераторы суперформул и сферических гармоник, а также добавил пару новых параметрических форм. Я также добавил новые параметры окраски вершин, еще несколько примеров, систему отмены / повтора для отслеживания изменений параметров и дополнительные параметры управления оболочкой.
Этот зритель, вероятно, был больше всего вдохновлен веб-страницами Пола Бурка о сферических гармониках и суперформуле, а также многими другими программами просмотра суперфигур, написанными другими. Поскольку многие из моих визуализаций производительности здания включают наложение данных анализа на цветные сетки в 3D-модели, я решил, что стоит потратить немного времени на их создание и анимацию как способ разработки и тестирования моих собственных библиотек сеток.
Интересные особенности
Я думаю, что наиболее интересными особенностями этого приложения являются:
Полная анимация переходов форм на графическом процессоре с использованием интерполирующих шейдеров,
Разработка ползунков данных на основе SVG, которые достаточно хорошо масштабируются и хорошо взаимодействуют на настольных и мобильных устройствах,
Немного поработав с параметрами каждой формы, чтобы случайная генерация была немного умнее,
Заставить мои вычисления силуэта фигур работать достаточно быстро в Javascript, и
Внедрение системы отмены / возврата для всего приложения.
Типы форм
Ниже приводится краткое описание каждого из реализованных в настоящее время типов фигур, а также некоторые полезные ссылки:
Сферические гармоники
Сферические гармоники относятся к серии уравнений для генерации частотных модуляций на поверхности сферы. В то время как декартовы гармоники являются функцией размеров X и Y, сферические гармоники являются функцией широтных и продольных углов. В конкретном случае использования здесь произвольное скалярное значение, отображаемое на сферической поверхности, используется для смещения вершин сферы для создания интересных трехмерных форм.
Для получения дополнительной информации см. Следующие ресурсы:
Сферические гармоники
действительно интересны, поскольку их можно использовать для уменьшения того, что обычно является чрезмерно дорогостоящей интеграцией среды рассеянного освещения в серию гораздо более быстрых точечных произведений. Это делается путем аппроксимации рассеянного освещения, заданного как сложное распределение света по интегрирующей сфере, с матрицей коэффициентов сферических гармоник.
Использование этой модели вместо стандартной модели диффузного отражения от поверхности может сделать возможными очень подробные и реалистичные эффекты диффузного освещения, близкие к реальному времени.Робин Грин объясняет это лучше и более подробно в книге «Сферическое гармоническое освещение: мелкие детали».
Формы суперформулы
Суперформ — это формы, созданные с использованием обобщения формулы суперэллипса Йохана Гилиса, часто называемой суперформулой. Это было предложено в 2003 году в качестве основы для моделирования естественных форм и в основном представляет собой уравнение с четырьмя входными параметрами, которые генерируют ряд естественно выглядящих многоугольников. Две суперформулы (отсюда восемь параметров) используются для создания сложных естественных трехмерных форм.Модулируя радиус и / или координаты Z, его также можно использовать для создания интересных оболочек, спиралей и спиралей.
Для получения дополнительной информации см. Следующие ресурсы:
Супер эллипсоид
Суперэллипсоид — это просто произведение двух уравнений суперэллипса в двух декартовых плоскостях, перпендикулярных друг другу. Результатом является трехмерная форма, которая может варьироваться от кубической, октаэдрической, пирамидальной, конической до асимптотически вогнутой.
Для получения дополнительной информации см. Следующие ресурсы:
Супер Тороид
Супер-тороид — это кольцеобразная поверхность вращения, созданная выдавливанием поперечного сечения суперэллипса вокруг пути другого суперэллипса.
Для получения дополнительной информации см. Следующий ресурс:
Эллиптический тор
Эллиптический тор — это еще одна кольцеобразная поверхность вращения, созданная путем вращения смещенного эллипса по круговой траектории. Параметры контролируют степень смещения и его эксцентриситет.
Для получения дополнительной информации см. Следующий ресурс:
История изменений
0,0.4
2019-09-16
Добавлена возможность вырезать поперечное сечение текущей формы и спроектировать ее внешнюю оболочку на любую плоскость.Кто-то попросил об этом, и это прозвучало как интересный маленький проект, так что вот он. Вы можете вращать плоскость, используя полярные углы, и смещать ее в этом направлении от центра формы, используя элементы управления в новом всплывающем окне
СЕКЦИЯ / ПРОЕКЦИЯ ПЛОСКОСТЬна верхней правой панели инструментов.Кроме того, я узнал немного больше о шейдерах с тех пор, как изначально делал это приложение, поэтому воспользовался возможностью, чтобы уточнить некоторые аспекты того, что используется здесь. Теперь их на пару меньше, и они немного быстрее и снисходительнее на старом / медленном оборудовании.
Эффект затенения краев, кажется, работает довольно хорошо, поэтому я удалил линейный силуэт, чтобы еще больше ускорить рендеринг и сделать его одинаковым во всех браузерах.
0,0.3
15.09.2017
Добавлен новый пункт меню
Export Geometry ...в менюSettings Data. Это позволяет экспортировать текущую форму как файл .OBJ , .STL или .PLY .Форматы .OBJ и .PLY могут включать цвета вершин, тогда как .STL их не поддерживает.Поскольку Chrome больше не поддерживает ширину линии WebGL на любой платформе (или в браузерах, основанных на ANGLE), к форме было добавлено дополнительное затенение краев, чтобы компенсировать отсутствие линейного силуэта.
0.0.2
2014-09-15
Добавлено новое меню
Slider Settingsв правом верхнем углу для настройки ввода ползунка.Добавлены « нормальных приращений » и « более точных приращений » для управления разрешением слайдера.
Добавлена возможность переключения « Обновление в реальном времени » при перетаскивании любого из ползунков.

 А также стоит приобрести высококачественный провод в резиновой или силиконовой изоляции. Этот элемент понадобится для надёжного соединения всех концов обмотки.
А также стоит приобрести высококачественный провод в резиновой или силиконовой изоляции. Этот элемент понадобится для надёжного соединения всех концов обмотки.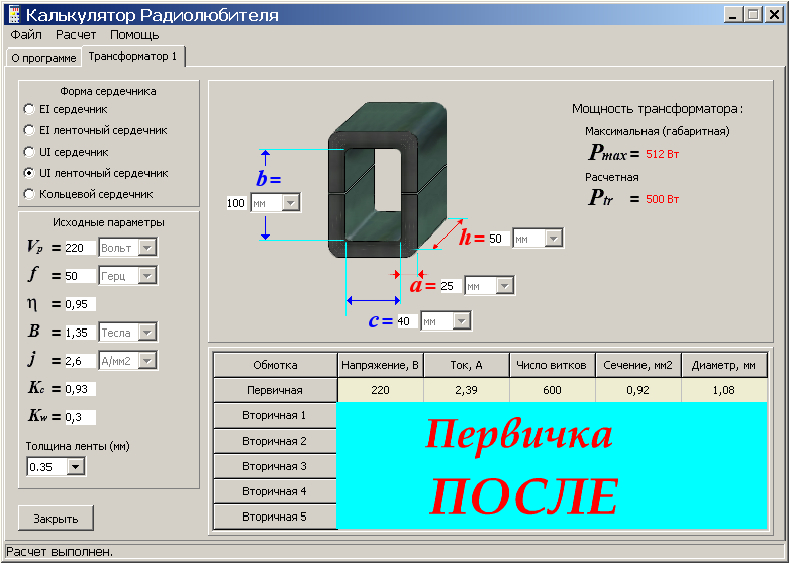
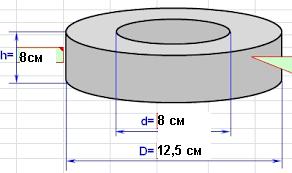 Уязвимую внутреннюю и внешнюю грань защищают картонными полосами с небольшими загибами по краям. Между первыми витками обмотки и сердечником должен присутствовать небольшой воздушный зазор. Такой подход особенно важен в тех случаях, когда края под проволокой протрутся. Так уязвимая токонесущая часть никогда не коснётся тороидального сердечника. На верхний слой обязательно наматывается киперная лента. В некоторых случаях мастера предпочитают сглаживать внешнее ребро колец, за счёт чего намотка углов идёт плавно.
Уязвимую внутреннюю и внешнюю грань защищают картонными полосами с небольшими загибами по краям. Между первыми витками обмотки и сердечником должен присутствовать небольшой воздушный зазор. Такой подход особенно важен в тех случаях, когда края под проволокой протрутся. Так уязвимая токонесущая часть никогда не коснётся тороидального сердечника. На верхний слой обязательно наматывается киперная лента. В некоторых случаях мастера предпочитают сглаживать внешнее ребро колец, за счёт чего намотка углов идёт плавно.